Похожие презентации:
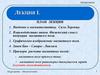
Сила Лоренца. (Лекции 15-16)
1.
Сила Лоренцаr
r r
Fл = q éë u´ B ùû
Hendrik Antoon Lorentz
1853 - 1928
Нидерланды
2.
Сила Лоренцаr
r r
Fл = q éë u´ B ùû
Fл = q uB sin a
r
Fл
q<0
r
B
q>0
r r
Fл ^ u
a r
u
r
Fл
Aл = 0
DWk = 0
u = сonst.
r
Fл
r r
a = an =
m
r
B
a r
u
r du r
at =
t=0
dt
Всегда !!!
3.
Движение заряженной частицы в однородном магнитном поле1.
2.
Fл = q uB sin a
r
B = const.
a=0
r
u
r
B = const.
a=p
2
r
Fл = 0
p
a = an = × v × B × sin = const
m
2
q
r
B
r
u
r
Fл
r
B
an = const
Равномерное дв-ие
по окружности
Ларморовский радиус
u2 q
an =
= ×u× B
R m
m×u
R=
q ×B
4.
r3. B = const. 0 < a < p
2
r
B
a
r
u^
h
a
r
Fл
Винтовая траектория с
радиусом R и шагом h
u^ = u sin a
uP = u cos a
mu^ 2
Fл = q uB sin a = q u^ B =
R
R
r
u
r r
r
u = u^ + uP
mu^ mu
R=
=
sin a
qB qB
5.
Эффект ХоллаEdwin Herbert Hall, 1855–1938
USA
6.
Эффект Холлаr
B
r
Fл
r
B
I
r
u
q
r
B
b
a
В = 0, поперечная разность потенциалов = 0
I
ЭДС Холла
В
r ≠0 r
Fл = - Fe
q uB = q E x
E x = uB
IB
Ux =
q na
7.
Эффект ХоллаIB
Ux =
q na
С помощью эффекта Холла
1. Измерение концентрации носителей тока:
В ЭДС Холла нет
в отличие от
2. Измерение знака носителей тока (по знаку ЭДС при данном
направлении тока ). Определения типа носителей в примесных
полупроводниках – электроны или дырки.
3. Измерение В: Ux ~ B
8.
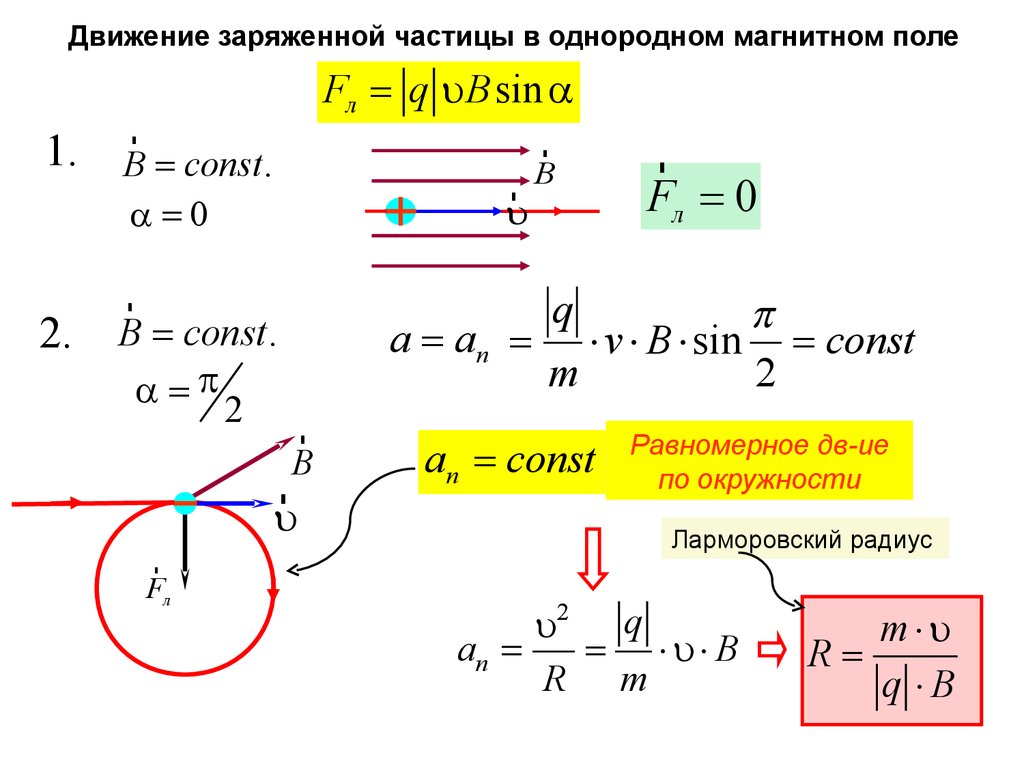
Сила АмпераСила Ампера - сила, действующая на проводник с током в магнитном
поле.
Сила Ампера - результирующая сил Лоренца, действующих на каждый
носитель тока в проводнике.
r
dFA
I
r
dFA
r
dl
r
B
dFA = NFл
N = ndlS
Fл = q uB sin a
r
r Fл
Fл
r
ur
u
r
B
r
dl
dFA = ndlS q uB sin a
q nuS = I
N – число носителей
тока в элементе длиной
dl и сечением S
dFA = IBdl sin a
r r
r
dFA = I éë dl ´ B ùû
Сила Ампера
9.
Взаимодействие двух параллельных бесконечно длинных прямыхпроводников с током в вакууме
I1
r
B1
r
I1dl1
r
dF12
r
m0 I 2
На I1dl1 в м.поле I 2 ( B2 =
)
r
dF21
r
I 2 dl2
r
B2
b
I2
Токи противоположного
направления отталкиваются
Токи одного направления
отталкиваются
dF12 dF21 m 0 I1 I 2
=
=
dl1
dl2
2p b
См. з-н Ампера
r r
r
dF12 = I1 éë dl1 ´ B2 ùû
2pb
r
m 0 I1
На I 2 dl2 в м.поле I1 ( B1 =
)
2pb
r r
r
dF21 = I 2 éë dl2 ´ B1 ùû
p m0 I 2 I 1
dF21 = I 2 dl2 B1 sin =
dl2
2 2p b
10.
Прямоугольный контур с током в однородном магн. полеПрямоугольный контур 1234 с током
F12 = 0
1
I
a
4
однородном магнитном поле
O
в
B ^ 14 и 23
B и нормалью
2
F14
M
I
F23
I
3
F34 = 0
b
O’
B
Между
1. B II плоскости рамки (sinα = π/2)
l34 II B
l12 II B
r r
r
dFA = I éë dl ´ B ùû
F12 = F34 = 0
F14 = - F23 ^ плоскости контура
Пара сил относительно
F14 и F23
оси ОО’
Вращающий момент
M
11.
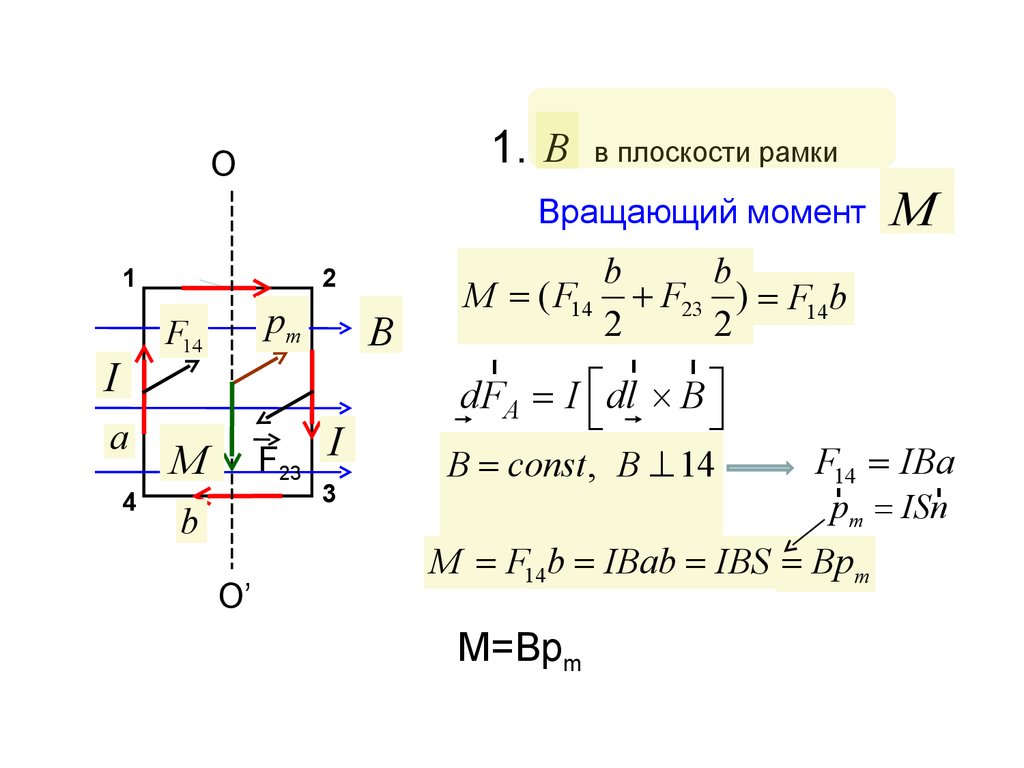
1. BO
в плоскости рамки
Вращающий момент
1
I
a
4
F14
pm
M
F23
b
O’
2
I
3
B
M
b
b
M = ( F14 + F23 ) = F14b
2
2
r r
r
dFA = I éë dl ´ B ùû
B = const , B ^ 14
F14 = IBa
r
r
pm = ISn
M = F14b = IBab = IBS = Bpm
M=Bpm
12.
2. B ^F12
2
1
F14
a I
4
3
b
F34
2
1
a I
4
I
b
3
B
плоскости рамки (sinα=0)
r r
r
dFA = I éë dl ´ B ùû
B
I
Между
B и нормалью
F23
F12 = - F34
F14 = - F23
Все силы в плоскости контура
M =0
Усилия на растяжение контура
Перемена направления I или B
сжатие контура
13.
3. BО
под углом α к нормали рамки (при этом
BII
B
a
B
p ^
I
m
О’
M
B = B^ + BII
B^ растяжение (сжатие) контура, M = 0
M = pm BII
BII
BII = B × sin a
M = [ pm B ]
Ось вращения лежит в
плоскости контура и
перпендикулярна
a =0
p
a=
2
a =p
B
устойчивое
B ^ 14 и 23 )
равновесие
max M
неустойчивое равновесие
M = pm B sin a
Справедливо для
контура любой формы
14.
ОРабота по повороту контура в магнитном поле,
потенциальная энергия контура в магнитном поле
B
a
I
pm
Поворот контура на угол dα под действием
.
сил Ампера
работа сил
Ампера
M = pm B sin a
dA = - Mda = - pm B sin a da
О’
M
a = 0 Wm = -p m B
Минимум энергии →
устойчивое положение
контура
a = p Wm = p m B
Максимум энергии →
неустойчивое положение
контура
a2
A = - ò p m Bsin ada = p m B(cos a 2 - cos a1 ) =
a1
= (- p m Bcos a1 ) - (- p m Bcos a 2 ) = Wm1 - Wm 2
Wm = - p m Bcos a + Const.
Const=0
Wm = - p m Bcos a
Потенциальная
энергия контура
с током в
магнитном поле
15.
Устойчивое положение контура в однородном магнитном полеr
dF
min Wm = - pm B
r
dF
r
B = const.
r
dF
I
r
pm
r
dF
r
dF
r
dF
r
dF
r
B
x
16.
Контур с током в неоднородном магнитном полеdB
a = 0, B ( x),
>0
dx
Силы Ампера ^ B и dl
dWп dWп dWп
F = - gradWп = -(
+
+
)
dx
dу
dz
dW
dW
п
dу
=
п
dz
=0
Wm = - pm B малый по
размерам контур
dB
dWm
втягивание
= pm
F = Fx = dx
dx
r
dB
dF
F = pm
>0
dx
r
B
I
0
r
pm
r
B
r
dF
r
F
x
dB
a = p , B ( x),
>0
dx
dWm
F = Fx = =
dx
= - pm
dB
<0
dx
выталкивание
Сила действующая на контур с
током малых размеров
17.
Контур с током в неоднородном магнитном полеОбщий случай
r
B ( x, y , z )
a 0, a p
r
¶Wm r ¶Wm r ¶Wm r
F = -(
i+
j+
k ) = - gradWm
¶x
¶y
¶z
Для малого по размерам контура с током
Wm = -p m Bcos a
скалярное
произведение
F = - grad ( - pm B cos a ) = grad ( pm B )
Обобщение:
Если какое-либо тело имеет магнитный момент
pm
, то независимо от
причин его обусловливающих, на это тело в неоднородном магнитном
поле будет действовать сила F = grad ( p
.
m B)
Пример: постоянные магниты, любые магнетики
18.
Поток вектора магнитной индукцииПоток вектора B - аналог потока вектора E в электростатике
r
B
S
dS
ar
S – произвольная поверхность
B ( x, y , z )
- индукция неоднородного
магнитного поля
n
dS – бесконечно малая площадка
B = const
в пределах dS
dΦ=BcosαdS=Bn dS
Ф = ò Bn dS
S
19.
rB = const.
Работа, совершаемая при перемещении
проводника с током в магнитном поле
r
B = const.
I
0
x
dx
Магнитный поток
пересекаемый
проводником
r
r
B ^ dl
p
FA = IlB sin = IlB
2
l × dx = dS
BdS = d
dA = FA dx = I × l × B × dx = I × B × dS = Id
dA = Id
При α ≠ π/2
плоскости контура
r r
r
dFA = I éë dl ´ B ùû
r
FA
l
B^
Справедливо и при
dA = I × l × Bn × dx
B const
dA = Id
Bn dS = d
A = ò Id =I ò d =ID
A = ID
(очевидно!)
Справедливо в
общем случае,
включая
проводник
произвольной
формы
20.
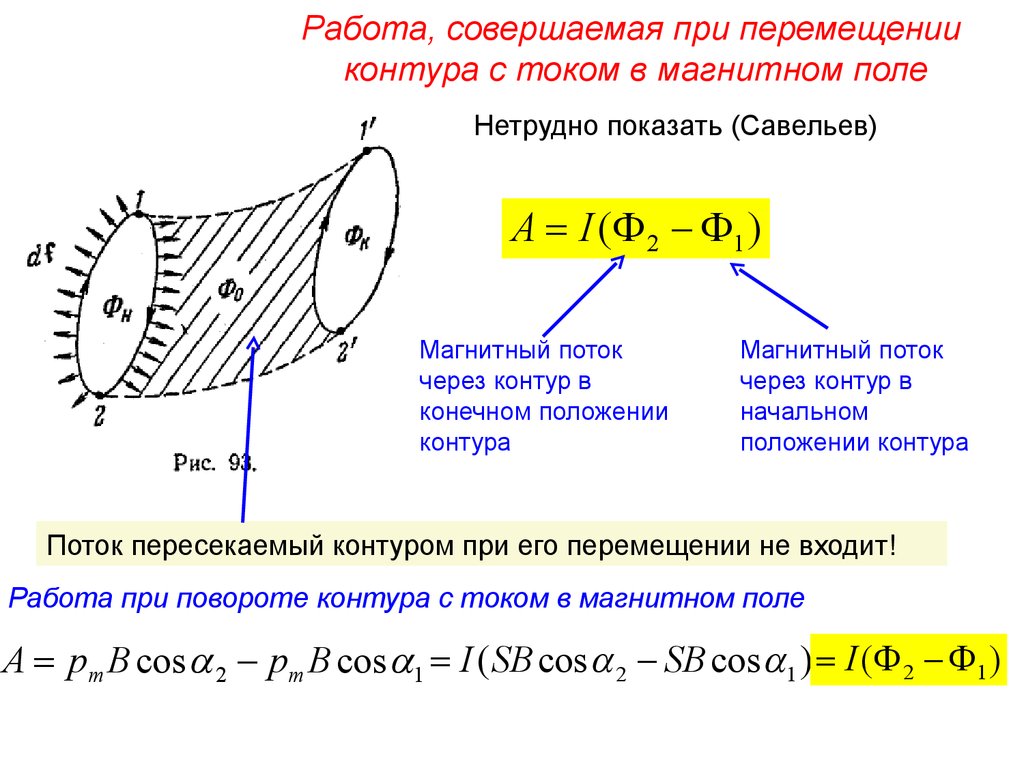
Работа, совершаемая при перемещенииконтура с током в магнитном поле
Нетрудно показать (Савельев)
A = I ( 2 - 1 )
Магнитный поток
через контур в
конечном положении
контура
Магнитный поток
через контур в
начальном
положении контура
Поток пересекаемый контуром при его перемещении не входит!
Работа при повороте контура с током в магнитном поле
A = pm B cos a 2 - pm B cos a1 = I ( SB cos a 2 - SB cos a1 ) = I ( 2 - 1 )
21.
Работа магнитного поля??Сила Лоренца не совершает работу!
r
r r
Fл = q éë u´ B ùû
r r
Fл ^ u
Магнитное поле не
совершает работу!
Aл = 0
Откуда берётся работа силы Ампера?
Работа силы Ампера совершается за счет энергии источника
питания, поддерживающего ток в контуре.
Изменение магнитного потока через контур
Ei = - dФ
dt
Работа против э.д.с. индукции
ЭДС индукции
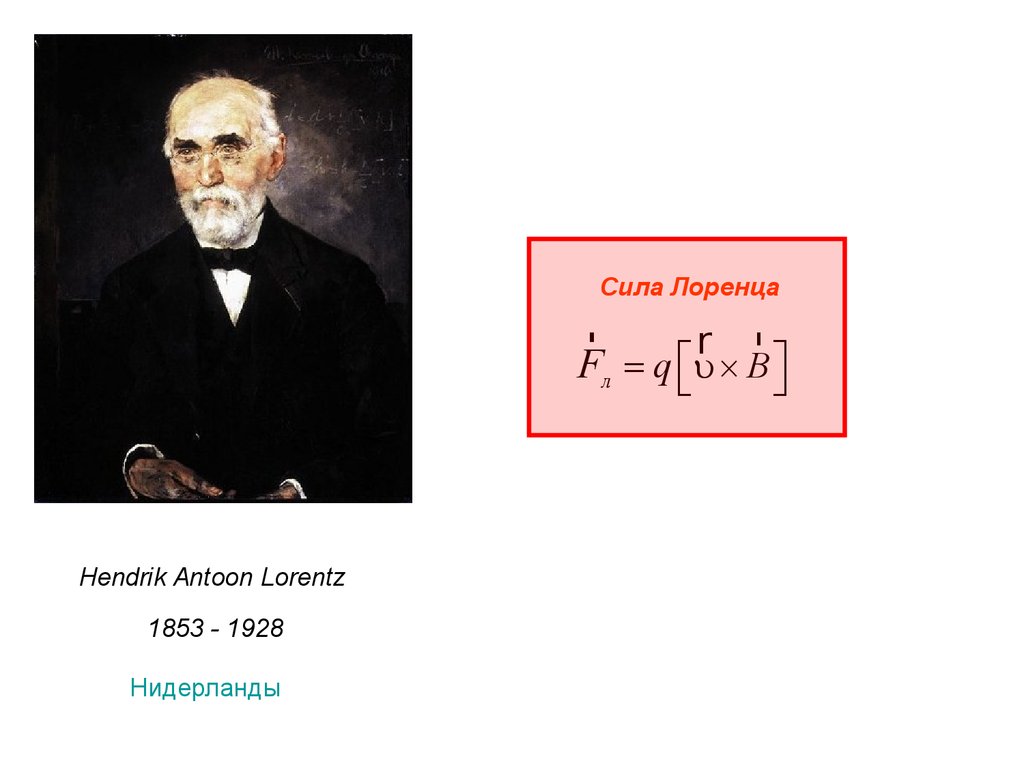
















 Физика
Физика