Похожие презентации:
Силы, действующие в магнитном поле: сила Ампера, сила Лоренца
1.
§ 22 Силы, действующие в магнитном поле:сила Ампера, сила Лоренца
Глава 3
Электричество и магнетизм
2.
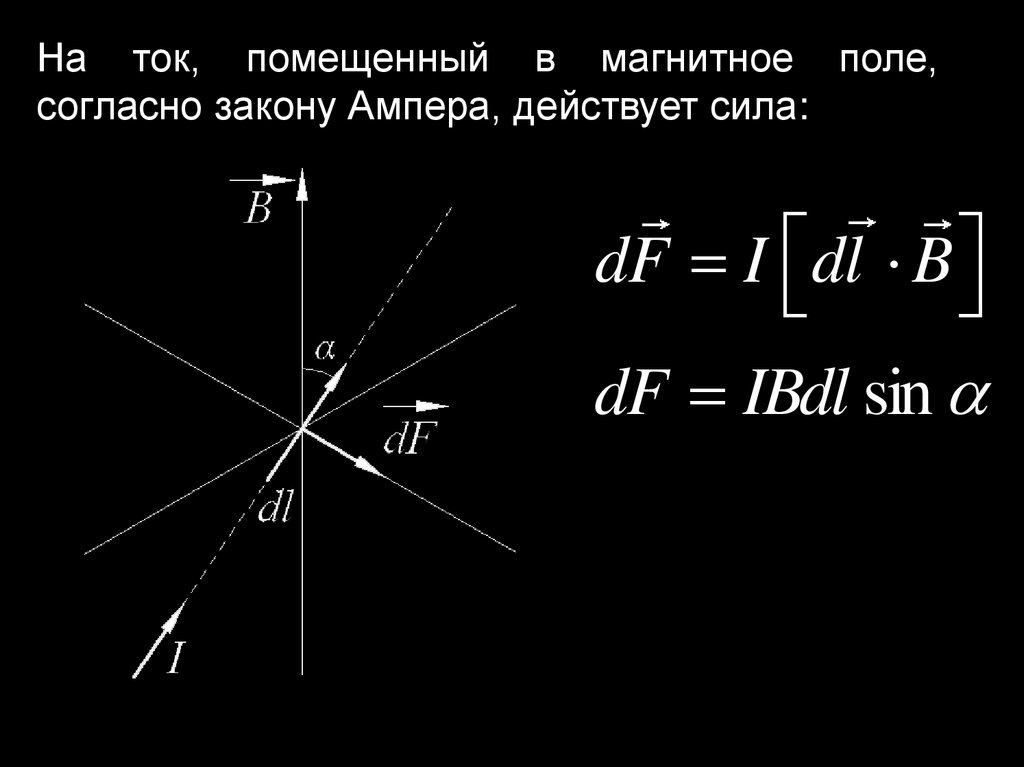
На ток, помещенный в магнитное поле,согласно закону Ампера, действует сила:
dF I dl B
dF IBdl sin
3.
С помощью закона Ампера можно определитьсилу взаимодействия двух параллельных токов
0 I1 I 2l
F
2 a
0 I1 I 2
F
2 a
*
I1 I 2
2 a
0
F
*
4.
Сила Лоренца представляет собой силу,действующую
на
элементарный
заряд,
движущейся в магнитном поле.
dF I dl B
Idl j Sdl qn Sdl
5.
dF qnSdl BdF
F q B
dN
6.
Fë q BFл q B sin
- сила Лоренца
7.
В магнитном поле заряд движется по окружности.Fл maц
q B m
2
R
8. Период вращения и радиус окружности в магнитном поле
2 R2 m
T
qB
(1)
m
R
qB
(2)
Движение частиц в магнитном поле является
синхронным, т.е. с одинаковым периодом. Радиус
окружности пропорционален скорости движения.
9.
При больших скоростях масса частиц зависитот скорости и синхронность нарушается.
m
m0
1
2
c2
10.
Ускорители элементарных частиц:1. Циклотрон . Период постоянен. Ускоряемые частицы –
протоны. Ускорение происходит между дуантами.
2. Фазотрон (синхроциклотрон). Изменяется частота
ускоряемого напряжения.
3. Синхротрон. Изменяется индукция поля. Для ускорения
электронов.
4. Синхрофазотрон. Изменяется частота ускоряемого
напряжения и индукция поля.
11.
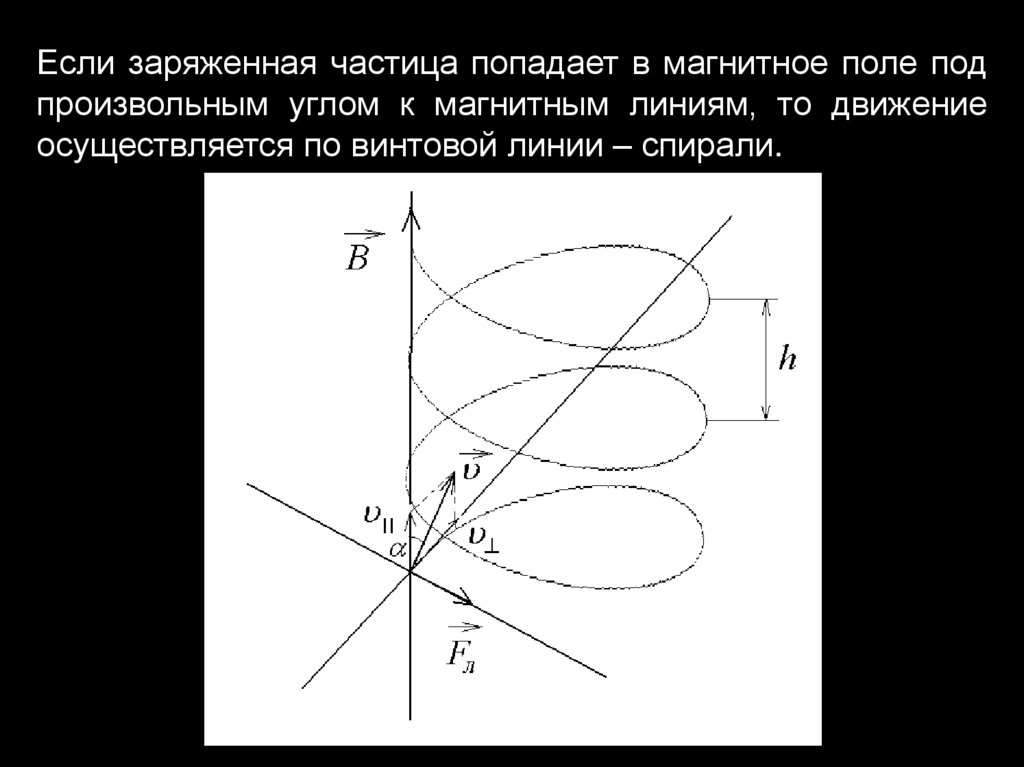
Если заряженная частица попадает в магнитное поле подпроизвольным углом к магнитным линиям, то движение
осуществляется по винтовой линии – спирали.
12.
Определим радиус винтовой линииFл maц
sin
q B sin m
R
m sin
R
q B
2
13.
Период обращения не зависит от угла2 R
2 m
T
sin
qB
Шаг винтовой линии
2 m cos
h ||T
qB
14.
При попадании в неоднородное магнитное полезаряды движутся по винтовой линии, накручиваясь на
нее. Примеры: северное сияние, магнитные ловушки,
магнитные линзы.
15. 23. Эффект Холла
16.
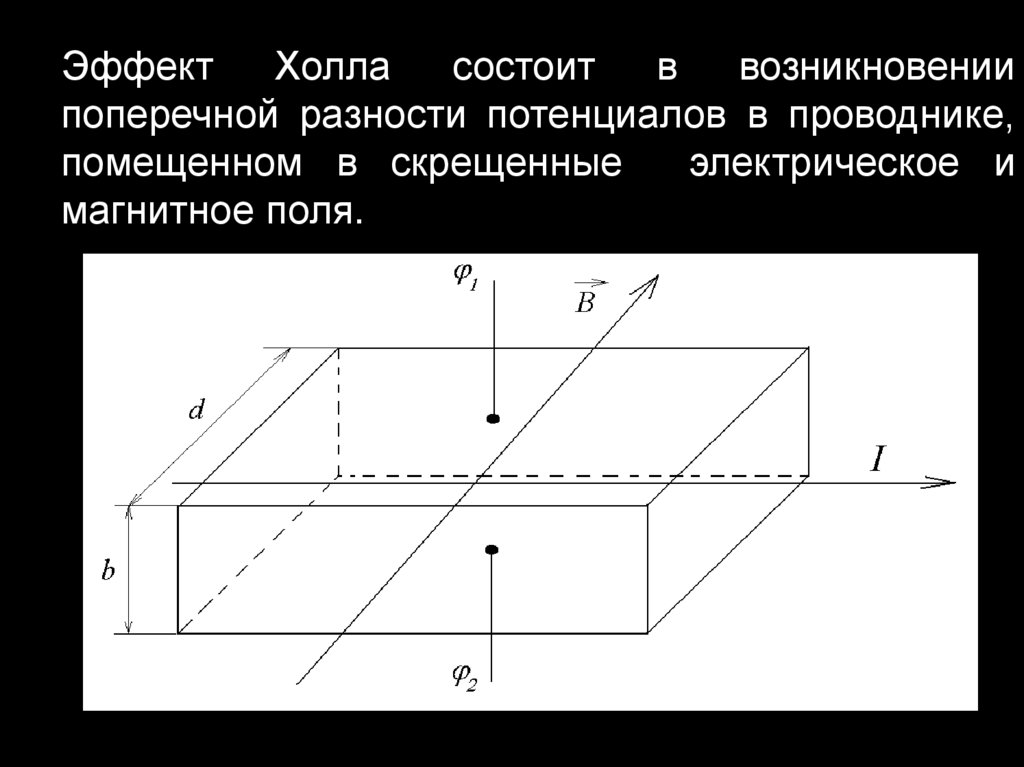
ЭффектХолла
состоит
в
возникновении
поперечной разности потенциалов в проводнике,
помещенном в скрещенные
электрическое и
магнитное поля.
17.
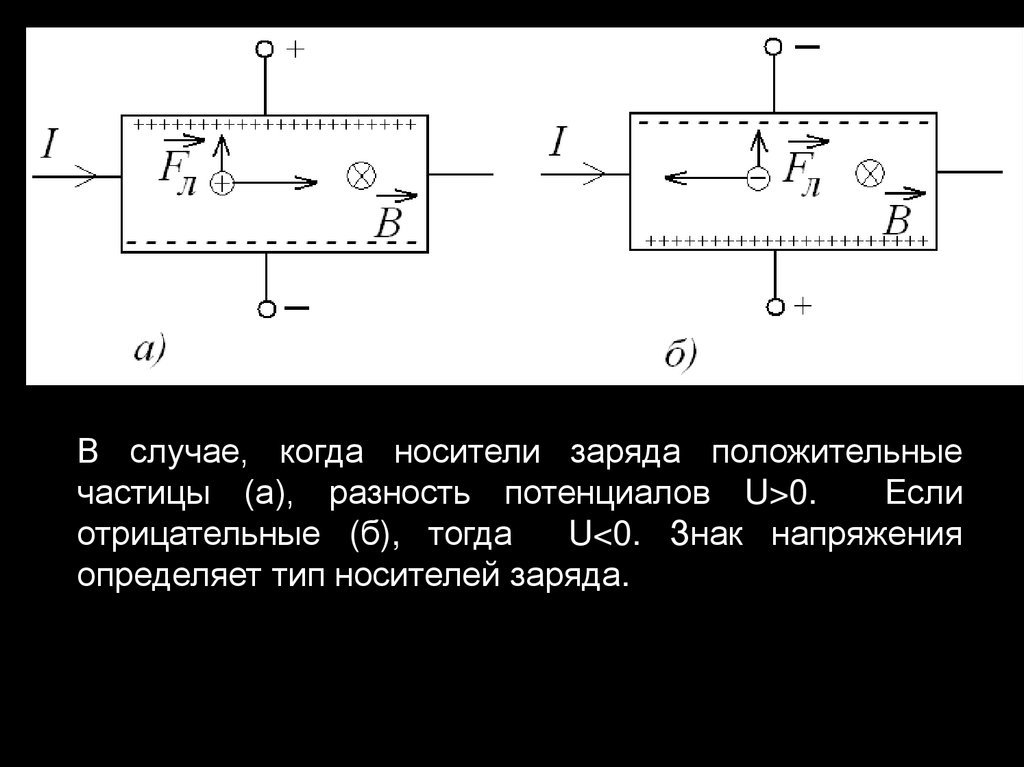
В случае, когда носители заряда положительныечастицы (а), разность потенциалов U>0.
Если
отрицательные (б), тогда
U<0. Знак напряжения
определяет тип носителей заряда.
18.
Возникшую разность потенциалов называют напряжениемХолла
U x 1 2
В установившемся режиме справедливо равенство сил
Fл Fэ
q B qE x
Учитывая
j
qn
Bj
E x B
qn
19.
Напряжение ХоллаПостоянная Холла
Rx BI
BI
Ux
qnd
d
1
Rx
qn
Постоянная Холла принимает более сложный вид при
понятии двух типов носителей заряда и при различных
температурах
20. Зная постоянную Холла и удельную проводимость можно определить подвижность носителей заряда.
qnRx
Rx
Rx
21.
Эффект Холла в сочетании с измерением удельнойпроводимости
позволяет
определить
основные
характеристики
проводника
концентрацию,
подвижность и тип носителей заряда. Проводя
измерения при различных температурах можно
исследовать механизмы рассеяния носителей заряда.
На эффекте Холла основана работа различных
датчиков магнитного поля, бесконтактное измерение
силы тока в проводниках, частотомеров, расходомеров,
бесконтактных
выключателей,
управление
двигателями, чтение магнитных кодов.
22.
24. Работа по перемещению контура ипроводника с током в магнитном поле
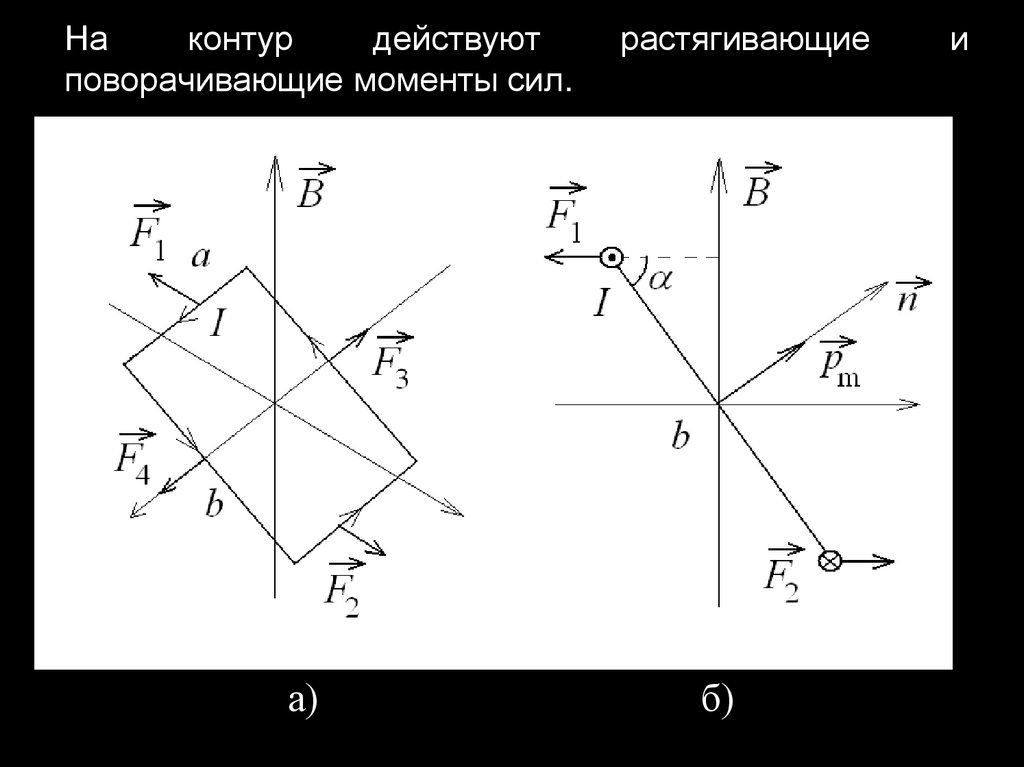
23. На контур действуют растягивающие и поворачивающие моменты сил.
Наконтур
действуют
поворачивающие моменты сил.
а)
растягивающие
б)
и
24.
Силы F1 и F2 стремятся повернуть рамку вокругоси х. Силы F3 и F4 растягивают, уравновешивая
друг друга. Суммарный момент сил:
M M 1 M 2 F1l1 F2l2
b
2 Ia B sin IabB sin
2
M pm B sin
25.
Вектор момента сил, действующих на рамку вмагнитном
поле
определяется
векторным
произведением:
M pm B
26.
При изменении угла совершается механическаяработа:
dA Md
dA pm B sin d
27.
Интегрируя по углу поворота, вычисляем работу:2
2
1
1
A pm B sin d pm B cos
pm B cos 2 pm B cos 1 W2 W1
28.
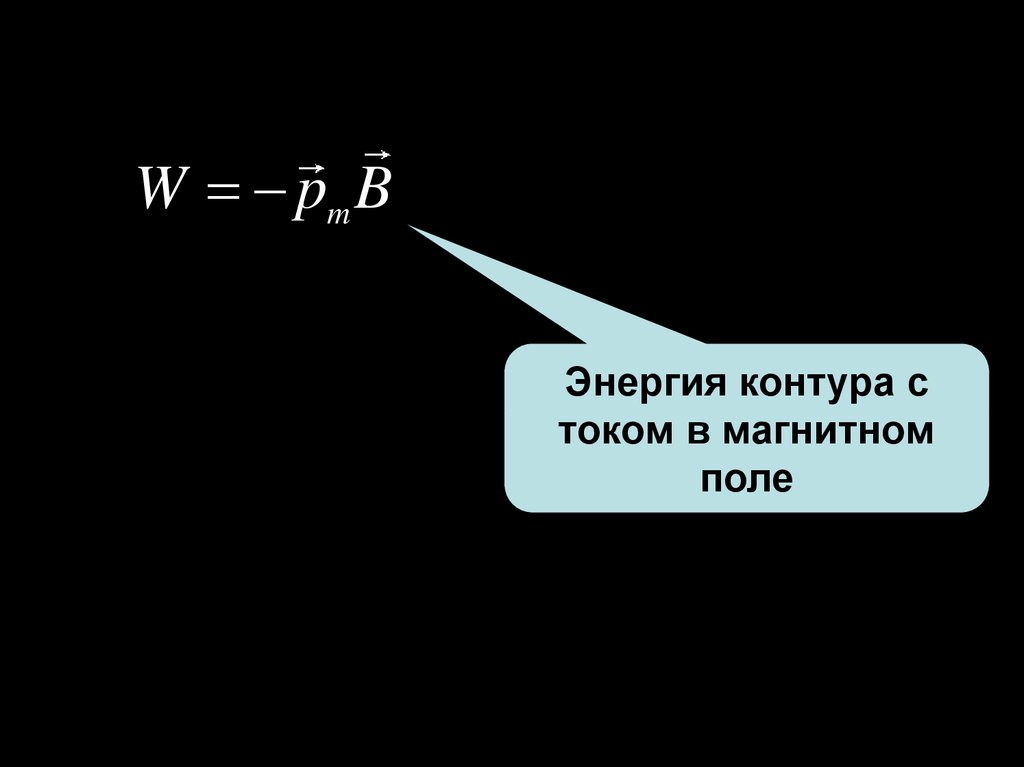
W pm BЭнергия контура с
током в магнитном
поле
29.
Работа при перемещении проводника с токомdA FAdx IBldx IBdS IdФ
dA IdФ
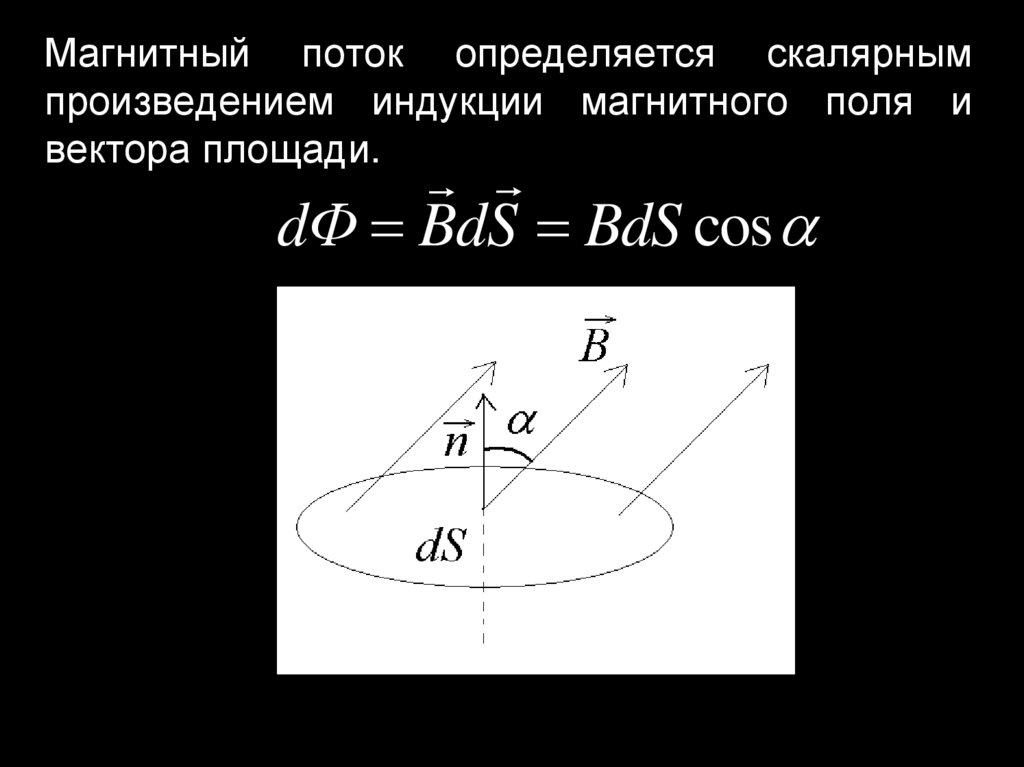
30. Магнитный поток определяется скалярным произведением индукции магнитного поля и вектора площади.
dФ BdS BdS cos31.
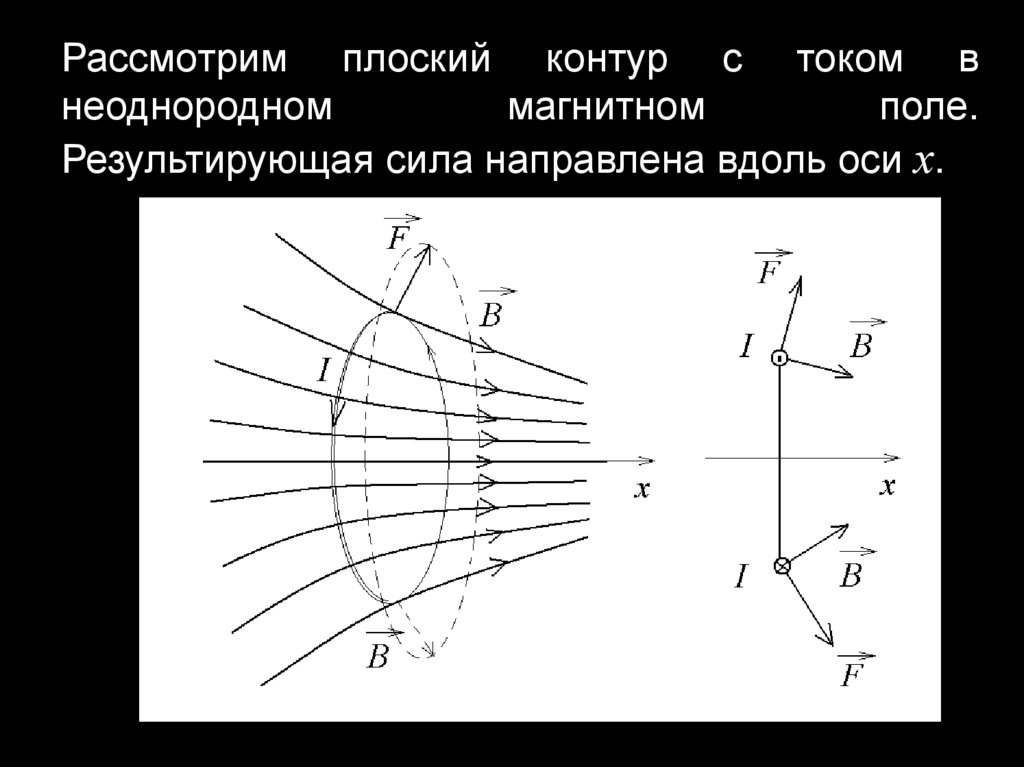
Рассмотрим плоский контур с током внеоднородном
магнитном
поле.
Результирующая сила направлена вдоль оси х.
32.
Для определения силы Fx можно воспользоватьсясоотношением между силой энергией:
dW
Fx = dx
W pm B pm B cos
33.
BFx p m cos
x
Проекция силы Fx пропорциональна градиенту
индукции магнитного поля.
Т.о. в магнитном поле контур ориентируется
магнитным моментом по полю и втягивается в
область сильного магнитного поля.



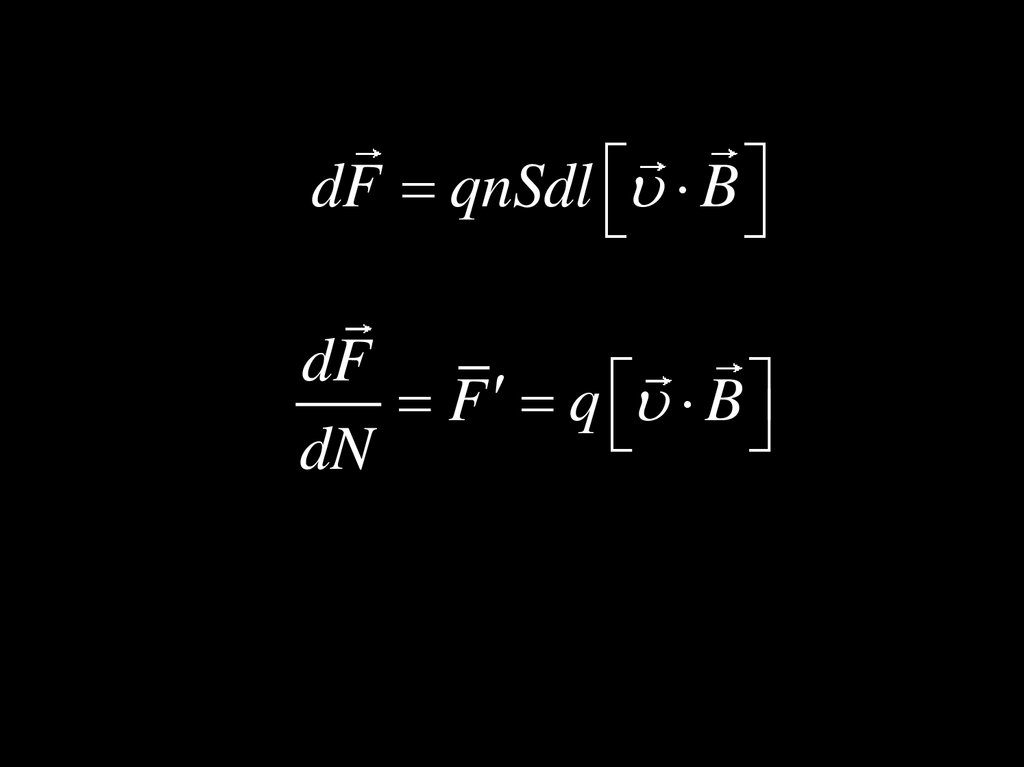



















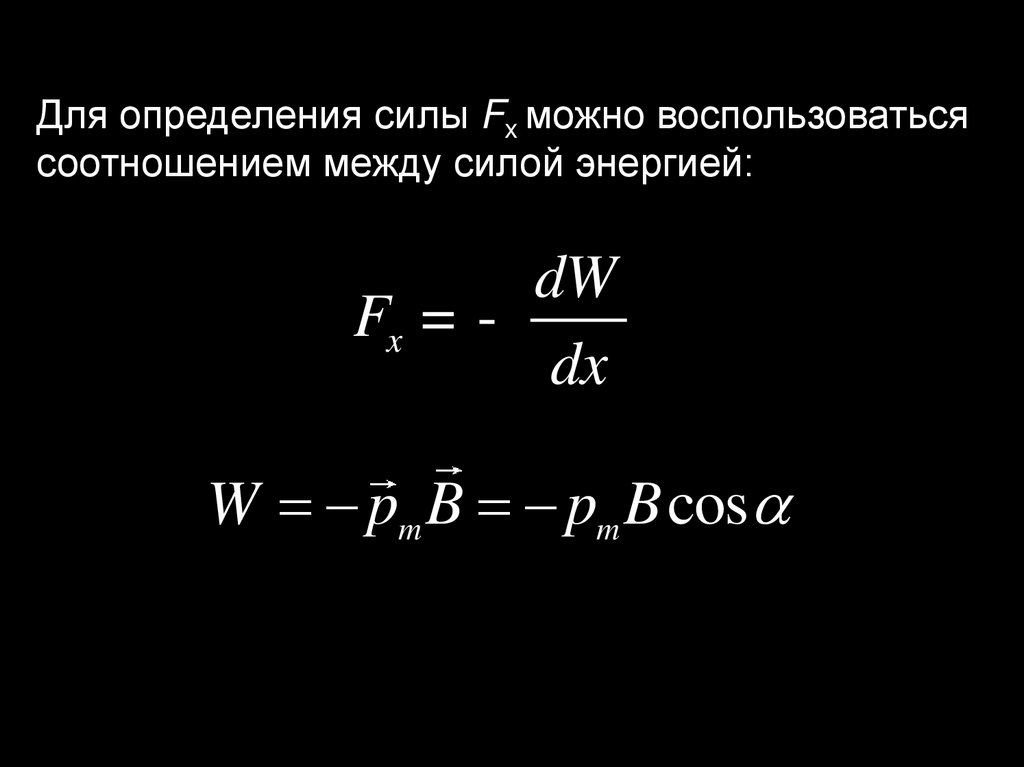

 Физика
Физика








