Похожие презентации:
Физические основы высоких технологий. (Колебания и волны)
1. ФИЗИЧЕСКИЕ ОСНОВЫ ВЫСОКИХ ТЕХНОЛОГИЙ (ЧАСТЬ 3)
(Колебания и волны)2. Колебания
Колебаниями называются процессы, отличающиеся той или инойстепенью повторяемости.
В зависимости от характера воздействия на колеблющуюся систему
различают свободные (или собственные) колебания и вынужденные
колебания.
Свободными называют такие колебания, которые происходят в
системе, предоставленной самой себе после того, как ей был
сообщен толчок либо она была выведена из положения равновесия.
Вынужденными называют такие колебания, в процессе которых
колеблющаяся система подвергается воздействию внешней
периодически изменяющейся силы.
3. Затухающие колебания
При движении тела в среде последняя всегда оказываетсопротивление, стремящееся замедлить движение.
При этом энергия движущегося тела, в конце концов, переходит в
тепло. В таких случаях говорят, что имеет место диссипации
энергии.
Если движение тела в среде достаточно медленное по сравнению со
скоростью внутренних диссипативных процессов, то реакция среды
на движение тела в некоторых случаях может быть приближенно
описана введением так называемой силы трения, действующей на
тело и зависящей лишь от скорости последнего. Такая ситуация
возникает, например, при движении тела в вязкой среде, жидкости
или газе.
4. Уравнение затухающих колебаний
В ряде случаев можно считать,пропорциональна величине скорости
что
сила
сопротивления
Fx,сопр. r v rx
где r ̶ коэффициент сопротивления или трения.
Уравнение второго закона Ньютона для одномерного движения в
присутствие сил сопротивления имеет вид:
mx Fупр Fсопр
mx kx rx
Перенося все слагаемые в одну сторону
mx rx kx 0
и разделив уравнение на массу тела, получаем
( Fупр kx)
5. Уравнение затухающих колебаний
xДанное уравнение
представить в виде :
r
k
x x 0
m
m
(уравнение
затухающих
колебаний)
можно
x 2 x 02 x 0
где
2
r
,
m
02
k
m
ω0 ̶ представляет собой ту частоту, с которой совершались бы
свободные колебания системы при отсутствии сопротивления среды,
т.е. при r=0.
Наличие сопротивления среды приводит к тому, что размах
колебаний уменьшается. Поэтому в зависимости смещения от
времени амплитуда колебаний должна изменяться.
6. Уравнение затухающих колебаний
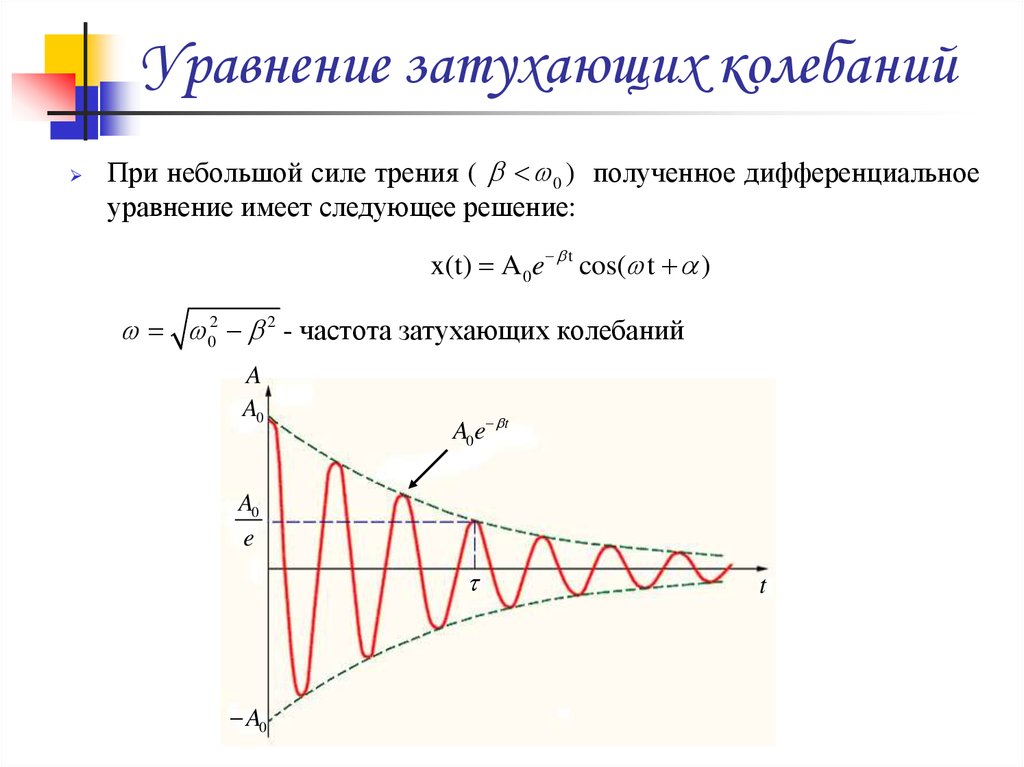
При небольшой силе трения ( 0 ) полученное дифференциальноеуравнение имеет следующее решение:
x(t) A 0 e t cos( t )
02 2 - частота затухающих колебаний
A
A0
A0e t
A0
e
A0
t
7. Коэффициент затухания
В соответствии с видом функции движение системы можнорассматривать как гармонические колебания частоты ω с
амплитудой, изменяющейся во времени по закону:
A(t) A 0 e t
x(t) A(t)cos( t )
Скорость затухания амплитуды колебаний определяется величиной
r
2m
которую называют коэффициентом затухания.
8. Коэффициент затухания
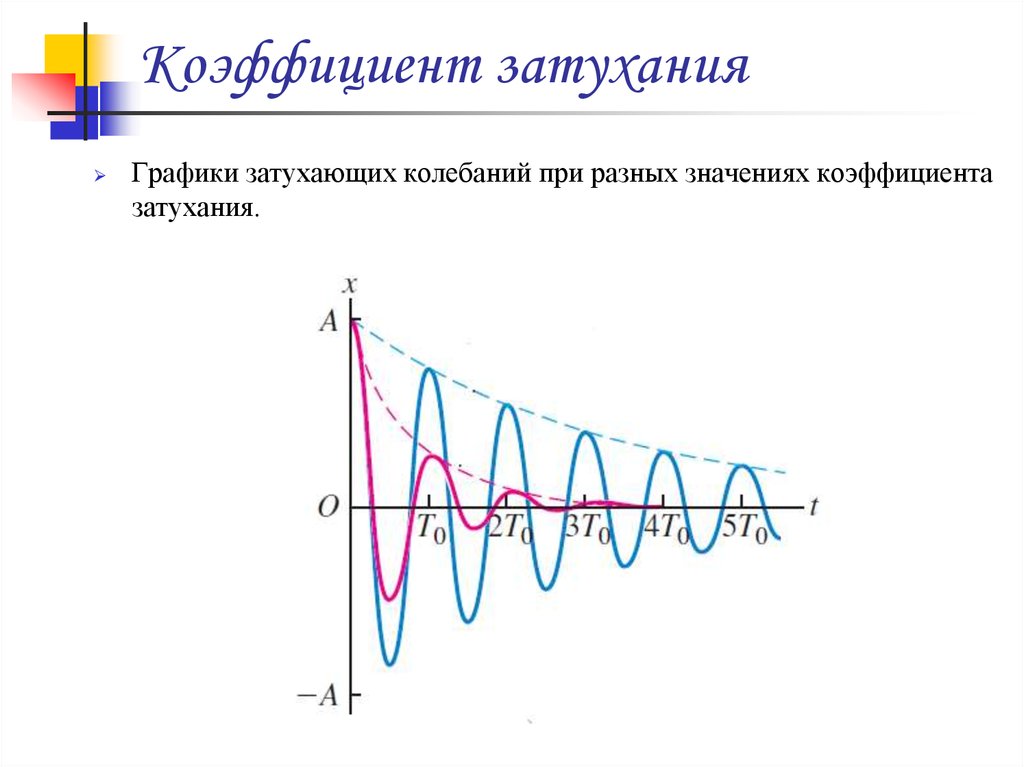
Графики затухающих колебаний при разных значениях коэффициентазатухания.
9. Время затухания
Найдем время τ, за которое амплитуда колебаний уменьшается в ераз.
A(t) A 0 e t
По условию
так как
A 0 /A( ) e
A( ) A 0 e
то
A0 / A( ) A0 / A0 e e
С учетом условия (*) получаем
Откуда
e e
1/
(*)
10. Время затухания
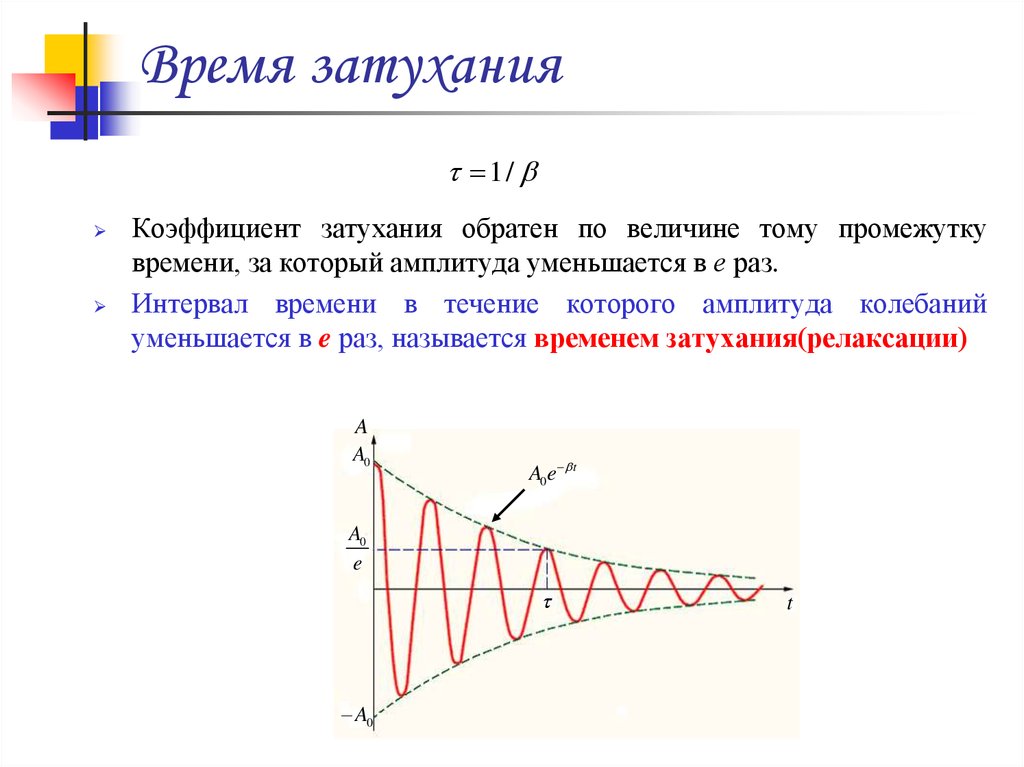
1/Коэффициент затухания обратен по величине тому промежутку
времени, за который амплитуда уменьшается в е раз.
Интервал времени в течение которого амплитуда колебаний
уменьшается в e раз, называется временем затухания(релаксации)
A
A0
A0e t
A0
e
A0
t
11. Период затухающих колебаний
Период затухающих колебаний равен:T0
2
T
2
02 2
1 / 0
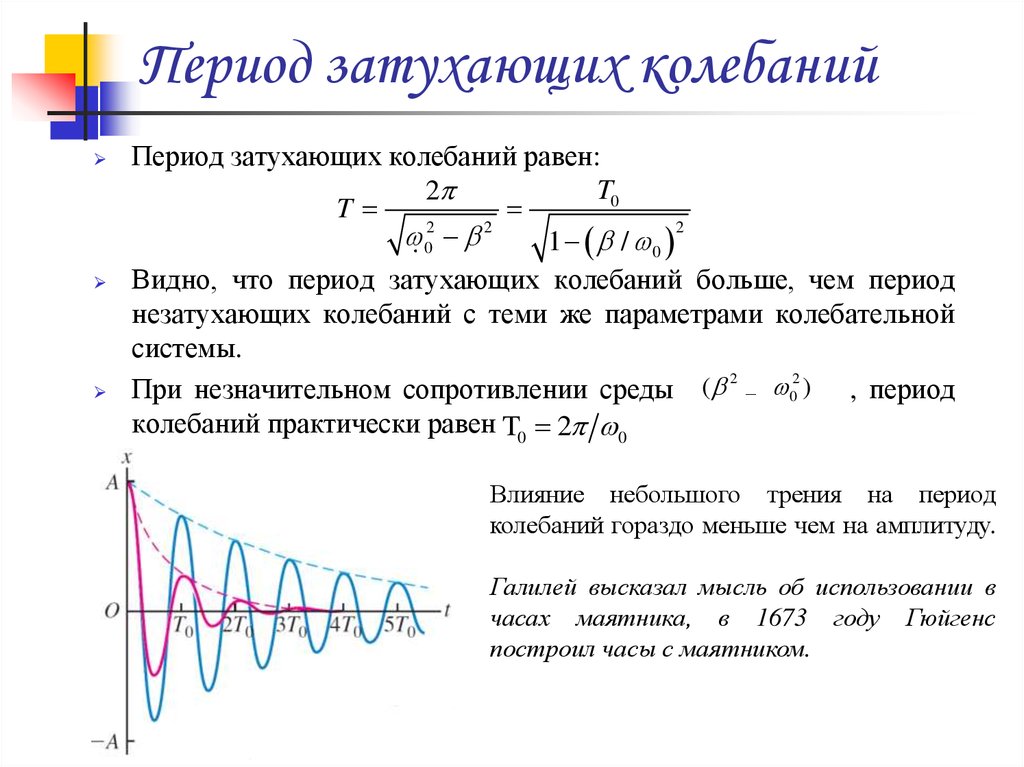
Видно, что период затухающих колебаний больше, чем период
незатухающих колебаний с теми же параметрами колебательной
системы.
2
02 ) , период
При незначительном сопротивлении среды (
колебаний практически равен T0 2 0
Влияние небольшого трения на период
колебаний гораздо меньше чем на амплитуду.
Галилей высказал мысль об использовании в
часах маятника, в 1673 году Гюйгенс
построил часы с маятником.
12. Декремент затухания
A(t) A 0 e tПоследующие наибольшие отклонения в какую-либо сторону
(например А’, А”, А”’ и т.д.) образуют геометрическую прогрессию.
Действительно, если
A A(t ) A0 e t ,
то
A A(t T ) A0 e (t+T) A0e t e T A e T ,
A A(t 2T ) A0 e ( t+2T) A e T
Видно, что отношение значений амплитуд, соответствующих
моментам времени, отличающимся на период, равно
A(t)
A
T
e
A t+T A e T
Это отношение называют декрементом затухания
13. Логарифмический декремент затухания
Логарифм декремента затухания – логарифмический декрементзатухания:
A(t)
ln
T
A(t+T)
Выразив β через λ и Т, / T закон убывания амплитуды можно
записать в виде:
A A0e
t
T
За время τ, за которое амплитуда уменьшается в е раз, система
успевает совершить Ne= τ/T колебаний. Из условия
e e
e
получается, что
T
e1
14. Логарифмический декремент затухания
TNe 1
или
1 / Ne
Видно, что логарифмический декремент затухания обратен по
величине числу колебаний, совершаемых за то время, за которое
амплитуда уменьшается в е раз.
Это дает наглядное представление о логарифмическом декременте
затухания. Пусть λ = 0,01, тогда примерно через 100 колебаний их
амплитуда уменьшится в е раз.
15. Добротность
Для характеристики колебательной системы часто употребляетсятакже величина:
Q
Ne
называемая добротностью колебательной системы. Как видно из ее
определения, добротность пропорциональна числу полных колебаний Ne,
совершаемых системой за время τ, за которое амплитуда колебаний
уменьшается в е раз.
16. Апериодические колебания
T2
02 2
С ростом коэффициента затухания β
период T затухающих
колебаний увеличивается.
При приближении коэффициента затухания (сопротивления среды) к
величине равной ω0
02 2 0
период колебаний обращается в бесконечность, т.е. движение
перестает быть периодическим. Анализ показывает, что при
02 2 0
колебания становятся апериодическими – выведенная из положения
равновесия система возвращается в положение равновесия, не
совершая колебаний.
17. Апериодические колебания
Запас механической энергии тела к моменту его возвращения вположение равновесия полностью расходуется на преодоление трения.
Демпфер – устройство для гашения
(демпфирования) или предотвращения
колебаний, возникающих в машинах,
приборах, системах или сооружениях
при их работе.
18. Вынужденные колебания
Если колебательная система подвергается воздействию внешнейпериодической силы, то возникают так называемые вынужденные
колебания, имеющие незатухающий характер.
Вынужденные колебания следует отличать от автоколебаний. В случае
автоколебаний в системе предполагается специальный механизм,
который в такт с собственными колебаниями "поставляет" в систему
небольшие порции энергии из некоторого резервуара энергии. Тем
самым поддерживаются собственные колебания, которые не затухают.
В случае автоколебаний система как бы сама себя подталкивает.
В случае вынужденных колебаний система подталкивается
посторонней силой. Особый интерес представляет случай, когда
внешняя сила, изменяющаяся по гармоническому закону с частотой ω,
воздействует на колебательную систему, способную совершать
собственные колебания на некоторой частоте ω0.
19. Уравнение вынужденных колебаний
Если свободные колебания происходят на частоте ω0, котораяопределяется параметрами системы, то установившиеся вынужденные
колебания всегда происходят на частоте ω внешней силы.
Уравнение второго закона Ньютона для колебательной системы, на
которую действует периодически изменяющаяся сила, будет иметь
вид:
mx kx rx F0 cos t
где F0 – амплитуда вынуждающей силы, ω - частота вынуждающей силы.
Разделив это уравнение на m, и перенеся члены с x в левую часть,
получим неоднородное линейное дифференциальное уравнение
второго порядка:
x 2 x 02 x f 0 cos t
20. Уравнение вынужденных колебаний
x 2 x 02 x f 0 cos tгде
f0
F0
m
Как решить это уравнение? В курсе математики доказывается, что
решение неоднородного дифференциального уравнения есть сумма
общего решения однородного уравнения и частного решения
неоднородного уравнения.
Общее решение однородного уравнения:
x A0 e t cos( t )
02 2
21. Амплитуда вынужденных колебаний
Частное решение неоднородного уравненияx A cos( t )
А – амплитуда вынужденных колебаний:
A
f0
( 02 2 ) 2 4 2 2
φ – представляет величину отставания по фазе вынужденного колебания
от обусловившей его вынуждающей силы
tan
2
02 2
22.
Полное решение уравнения вынужденных колебанийx A0 e t cos( t )
2
cos t arctan 2
2
( 02 2 ) 2 4 2 2
0
F0 / m
Анализируя решение, можно ввести два временных отрезка при
рассмотрении колебаний системы.
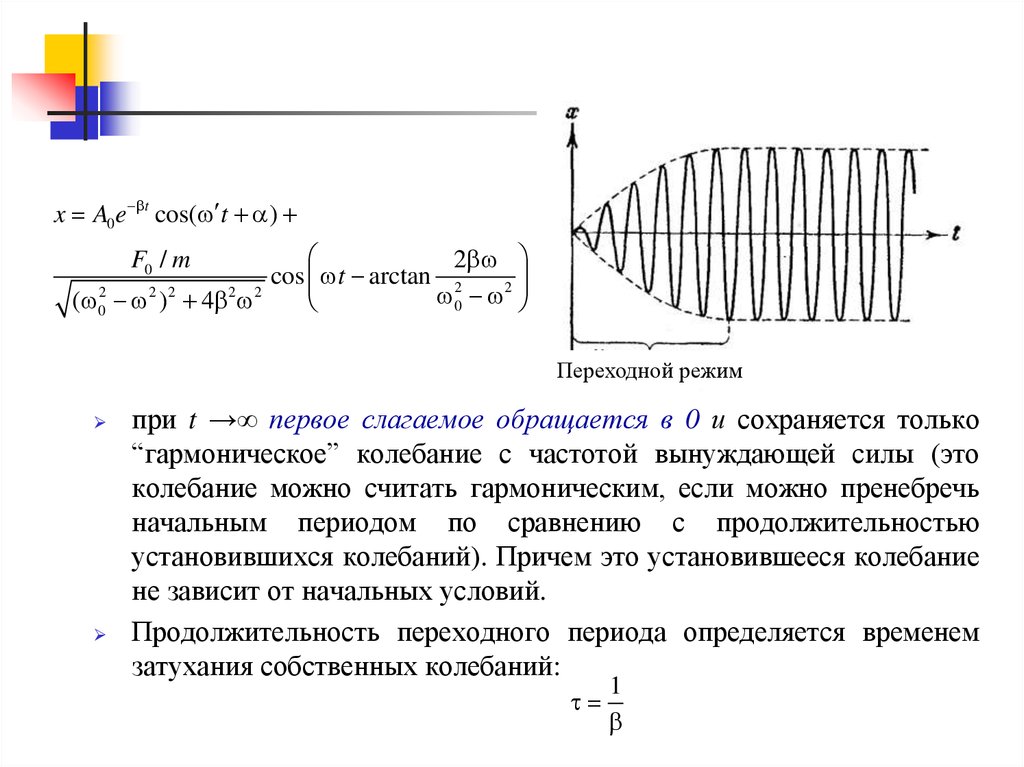
Переходной режим ‒ процесс установления колебаний, при котором
первое слагаемое дает еще существенный вклад в решение x(t).
При больших временах t от момента начала колебаний имеем дело с
установившимися колебаниями.
23.
x A0e t cos( t )2
cos t arctan 2
0 2
( 02 2 ) 2 4 2 2
F0 / m
Переходной режим
при t →∞ первое слагаемое обращается в 0 и сохраняется только
“гармоническое” колебание с частотой вынуждающей силы (это
колебание можно считать гармоническим, если можно пренебречь
начальным периодом по сравнению с продолжительностью
установившихся колебаний). Причем это установившееся колебание
не зависит от начальных условий.
Продолжительность переходного периода определяется временем
затухания собственных колебаний:
1
24. Резонанс
При некоторой частоте амплитуда вынужденных колебанийA
f0
( 02 2 ) 2 4 2 2
достигает максимума.
Колебательная система оказывается особенно отзывчивой на действие
вынуждающей силы при этой частоте.
Явление, при котором амплитуда колебаний резко возрастает,
называется – явление резонанса.
Соответствующая частота – резонансной частотой.
25. Резонансная частота
Максимум амплитуды определяется минимумом знаменателя. Дляопределения резонансной частоты
вычислим производную
знаменателя по частоте ω и приравниваем ее к 0:
d
( 02 2 ) 2 4 2 2 0
d
4( 02 2 ) 8 2 0
Уравнение имеет три решения:
0
02 2 2
Решение равное нулю, соответствует максимуму знаменателя.
Отрицательное должно быть отброшено, как не имеющее
физического смысла.
26. Резонансная частота
Для резонансной частоты получается:рез 02 2 2
Напомним
A
f0
( 02 2 ) 2 4 2 2
Соответственно амплитуда при резонансе
Aрез
f0
2 02 2
27. Резонансные кривые
Кривая, описывающая зависимость амплитуды А вынужденныхустановившихся колебаний от частоты внешней силы, называется
амплитудно-частотной характеристикой.
β1 < β 2 < β3
Чем меньше коэффициент затухания β (небольшое затухание), тем
ближе резонансная частота к частоте собственных колебаний, тем
выше значение амплитуды в максимуме.
Чем меньше коэффициент затухания β, тем уже резонанс и выше
величина максимума амплитуды.
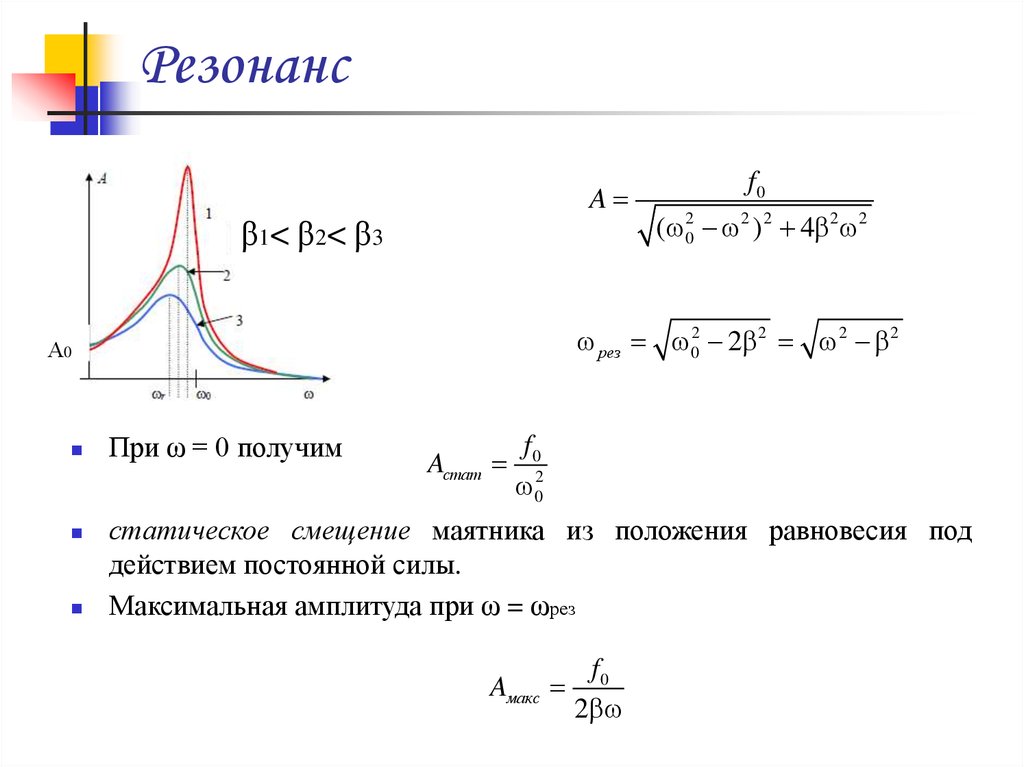
28. Резонанс
Aβ1 < β2 < β3
( 02 2 ) 2 4 2 2
рез 02 2 2 2 2
А0
f0
При ω = 0 получим
Aстат
f0
2
0
статическое смещение маятника из положения равновесия под
действием постоянной силы.
Максимальная амплитуда при ω = ωрез
Aмакс
f0
2
29. Резонанс
Найдет отношение Амакс/Астат:f0
2
Aстат
T
Q
Aмакс
Aмакс / Aстат
f0
02
2
Q 2
0
если β<<ω0
Aмакс / Aстат
Q
30. Примеры резонансов
Резонанс можно наблюдать в акустике, оптике, астрофизике и вомногих других областях науки, а также в природе.
Полезен ли резонанс?
Явление резонанса нужно учитывать на практике. В одних случаях он
может быть полезен в других – вреден. Резонансные явления могут
вызывать необратимые разрушения в различных механических
системах, например, неправильно спроектированных мостах.
Так, в 1940 году разрушился Такомский мост в США, спроектированный
без учёта ветровой нагрузки.
Ранее, в 1905 году, рухнул Египетский мост в Санкт-Петербурге, когда по
нему проходил конный эскадрон, причиной чего также считают резонанс,
хотя расчётами это не подтверждается. Тем не менее, существует
правило, заставляющее строй солдат сбивать шаг при прохождении
мостов.
20 мая 2010 года в Волгограде затанцевал мост. По официальной версии
мост вошёл в резонанс под действием ветровых нагрузок
31. Примеры резонансов
Такомский мост32. Вред и польза резонанса
Полезные свойства:Резонаторы в музыкальных инструментах
Магнитно-резонансное обследование организма
Раскачивание качелей. Выталкивание машины, когда она застряла
Раскачивание языка колокола
Резонансные замки и ключи
Радиоприёмники
Отрицательные свойства:
Разрушение сооружений
Обрыв проводов
Расплескивание воды из ведра
Раскачивание вагона на стыках рельсов
Вибрации в трубопроводах
Раскачивание груза на подъёмном кране
33. Вред и польза резонанса
Существует несколькоявления резонанса:
Уклонение
колебаний.
от
возможностей предотвращения
резонанса
путем
изменения
частоты
вредного
собственных
Организация взаимного гашения двух (или более) вредных действий.
Введение второго внешнего действия в противофазе к вредному.
Самонейтрализация вредного действия путем его разделения на два,
сдвига одного из них по фазе и их столкновение.
Самонейтрализация вредного действия путем введения дополнительных
грузов со смещающимся центром тяжести.
Ликвидация источника внешнего действия.
34. Видео
https://www.youtube.com/watch?time_continue=8&v=_XbGCogAOgchttps://www.youtube.com/watch?v=ux27Dovb9Fs
https://www.youtube.com/watch?v=uB91f6DGTVQ
35. Автоколебания
При затухающих колебаниях энергия системы расходуется напреодоление сопротивления среды. Если восполнять эту убыль
энергии, колебания станут незатухающими. Пополнение энергии
системы может осуществляться за счет толчков извне, однако эти
толчки должны сообщаться системе в такт с ее колебаниями, иначе
они могут уменьшить колебания системы и даже прекратить их
совсем.
Можно сделать так, чтобы колеблющаяся система сама управляла
внешним воздействием, обеспечивая согласованность сообщаемых
ей толчков со своим движением. Такая система называется
автоколебательной, а совершаемые ею незатухающие колебания –
автоколебаниями.
36. Видео
https://www.youtube.com/watch?time_continue=13&v=CX3hVy98h3837. Параметрические колебания
Характеристики или свойства колебательных систем описываютсявеличинами, называемыми параметрами.
Так, математический маятник характеризуется одним параметром длиной. Если изменять какой-либо параметр в определенном такте с
колебаниями, то можно сообщить маятнику энергию и тем самым
поддерживать колебания в незатухающем режиме. Такое
возбуждение
и
поддержание
колебаний
называется
параметрическим.
Примеры:
1) Качели. Колебания поддерживаются мускульной силой,
изменяющей центр тяжести системы.
2) Маятник на нити, длину которой меняют в такт с колебаниями.
38. Видео
https://www.youtube.com/watch?time_continue=30&v=XniyoaHLF7439. Блиц-опрос
Определить период колебаний груза на пружине, если жесткостьпружины 40 Н/м, а масса груза 0,4 кг.
1) 10 c
3) 0,628 c
Как будет изменяться частота математического маятника, если
поднять его над поверхностью Земли
1) увеличится
3) не изменится
2) уменьшится
4) недостаточно данных
Мальчик, качающийся на качелях, проходит положение равновесия
30 раз в минуту. Найти частоту колебаний
1) 0,25 Гц
3) 1,0 Гц
2) 6,28 с
4) 0,1 с
2) 0,5 Гц
4) 0,12 Гц
Максимальное отклонение тела от положения равновесия называется
1) амплитуда
3) период
2) смещение
4) частота
40. Блиц-опрос
Складываются два гармонических колебания одного направления,имеющие одинаковую частоту и одинаковую амплитуду.
Результирующие колебание имеет максимальную амплитуду при
разности фаз, равной …
1) 0
3) π/2
2) π
5) π/4
Материальная точка массой 2 кг совершает колебания по закону
x = 2,5 cos(2t+π/2) (м). Определите максимальную скорость точки.
1) 2,5
2) 5
3) 2,5π
4) 10


































 Физика
Физика








