Похожие презентации:
Механические колебания. Реальные колебания
1.
2. Реальные колебания.
Реальные свободные колебанияявляются затухающими из за действия
в системе сил трения. Простейшим
механизмом убыли энергии колебания в
механических системах превращение
ее в теплоту вследствие трения.
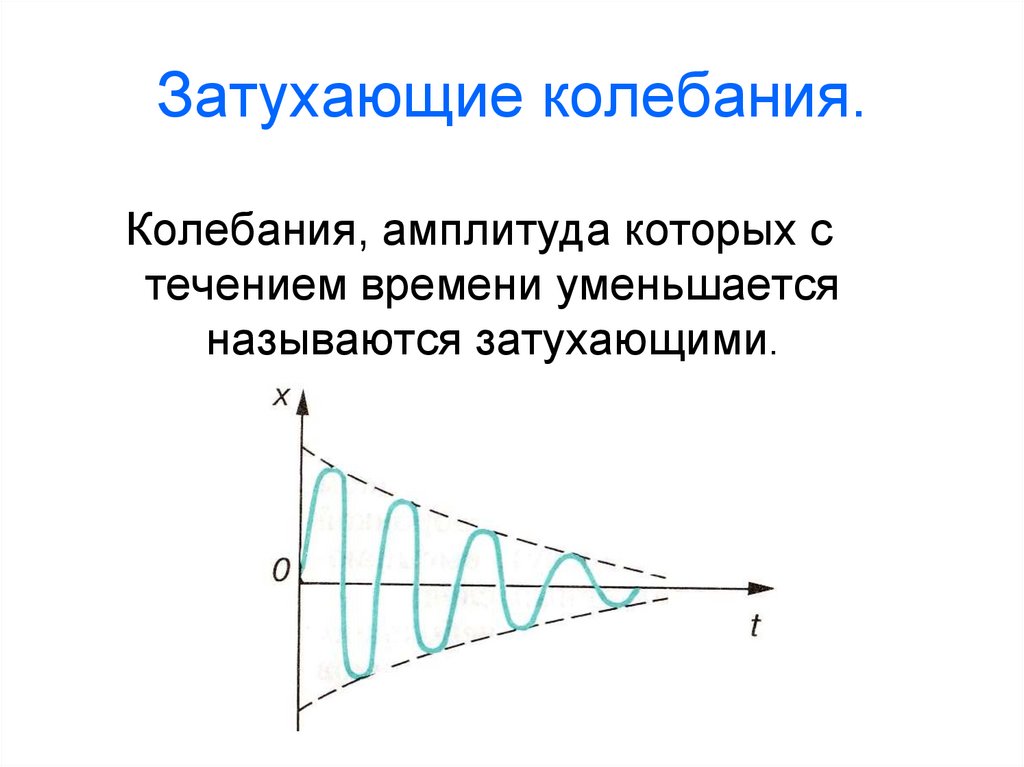
3. Затухающие колебания.
Колебания, амплитуда которых стечением времени уменьшается
называются затухающими.
4.
Если сила трения в колебательной системеимеет вид
Fтр r rx
то затухания происходят по
экспоненциальному закону (закону
экспоненты).
5. Уравнение затухающих колебаний.
Fynp kxFтp rx
mx kx rx
r
k
x x x 0
m
m
6.
x 2 x x 02
0
Решение имеет вид
x x0 e
t
cos( 0t )
7.
Сравнивая уравнения не трудно заметить, чтоr
2m
k
0
m
Коэффициент затухания
Циклическая частота
8. Характеристики затухающих колебаний:
t1) Амплитуда:
A A0e
2) Частота:
0
3) Период:
2
0
T
2
T0
2
9. 4) Время релаксации
Время, за которое амплитуда уменьшается в(минимальное число) ехр раз, называется
временем релаксации
t1
A1 A0e
exp
t
t
e
1
2
t 2
A2 A0e
t2 t1
10.
1Время релаксации обратно
пропорционально декременту колебаний и
показывает время необходимое системе для
полной релаксации (восстановления).
11. 5) Логарифмический декремент колебаний
A tln
T
A t T
Логарифм отношения двух амплитуд,
отстоящих друг от друга на время, равное
одному периоду, называется
логарифмическим декрементом колебаний.
12.
1N
Логарифмический декремент затухания
обратно пропорционален числу колебаний,
совершаемых за время релаксации, то есть в
течение, которого амплитуда уменьшается в ехр
(экспоненту) раз.
13.
6) Добротность колебательной системыДобротность — параметр колебательной
системы, определяющий ширину резонанса и
характеризующий, во сколько раз запасы
энергии в системе больше, чем потери энергии
за время изменения фазы на 1 радиан.
2 W (t )
W (t T ) T T
14.
Добротность системы тем выше, чем большеечисло колебаний успевает совершиться прежде,
чем амплитуда уменьшится в ехр раз.
Добротность обратно пропорциональна скорости
затухания собственных колебаний в системе, то
есть, чем выше добротность колебательной
системы, тем меньше потери энергии за каждый
период и тем медленнее затухают колебания.
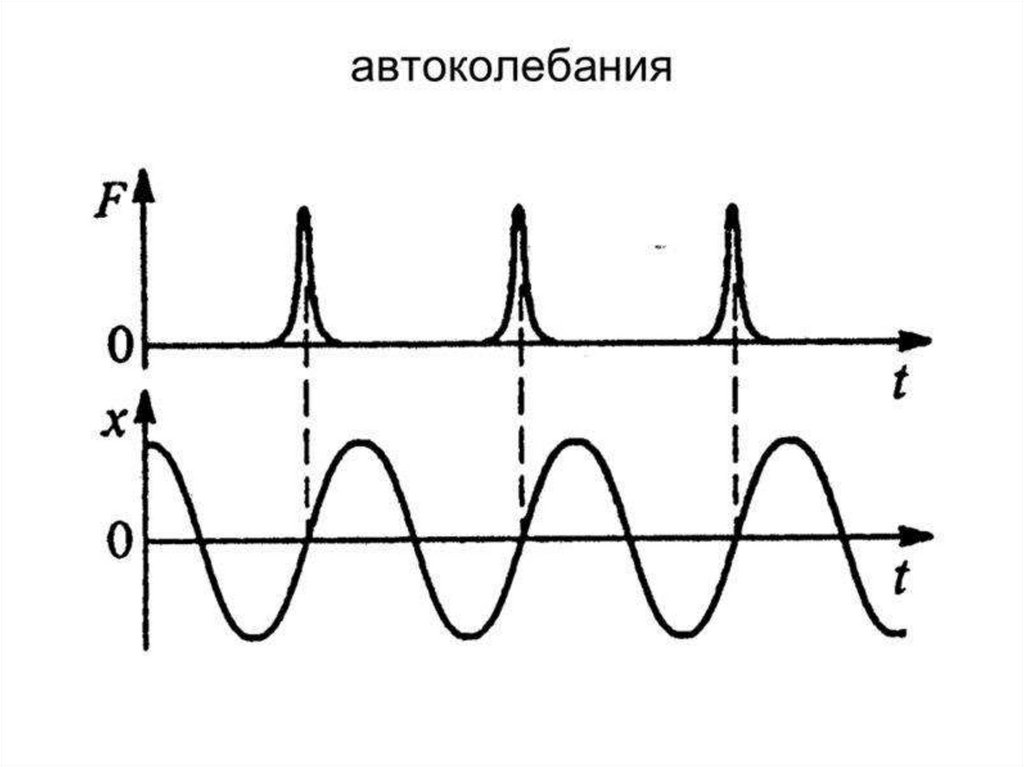
15. Автоколебания -
Автоколебания незатухающиеколебания
физической
системы,
существующие без
воздействия на нее
внешних сил.
16.
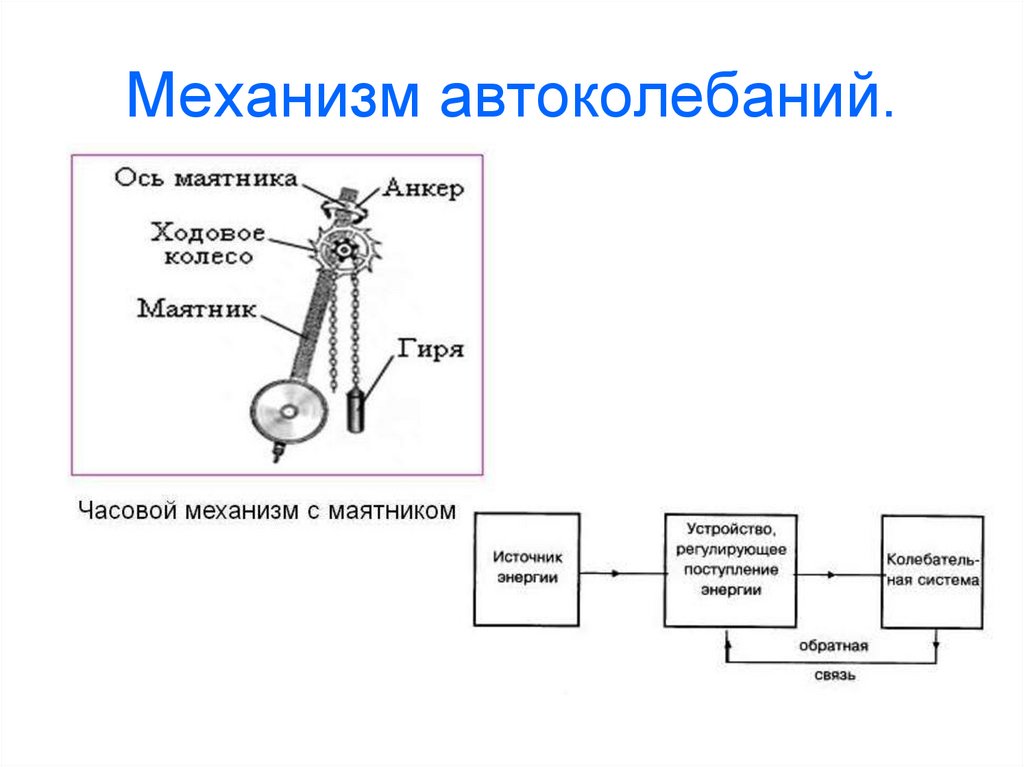
17. Механизм автоколебаний.
18.
Для получения незатухающих колебанийнеобходимо вводить энергию из вне, для
компенсации ее потерь в самой системе, то
есть на колебательную систему должна
действовать периодически изменяющаяся
внешняя сила, пополняющая систему
энергией.
Если на систему из вне действует сила, то
говорят о вынужденных колебаниях.
19. Вынужденные колебания.
Интересен случай внешней периодическименяющийся силы или силы изменяющийся
по гармоническому закону:
F f cos t
20. Уравнения вынужденных колебаний:
mx kx rx f cos t2
x 2 x 0 x h cos t 0
причем
r
2 m
и
k
0
m
f
h
m
21. Особенность вынужденных колебаний:
• Характер вынужденных колебанийопределяется свойствами внешнего
воздействия и самой системой,
совершающей колебания.
22. Особенность вынужденных колебаний:
• Частота и период вынужденныхколебаний равен частоте и периоду
вынуждающей силы. Вынуждающая
сила устанавливает свою частоту в
колебательной системе.
23. Особенность вынужденных колебаний:
• Амплитуда вынужденных колебанийзависит от амплитуды действующей
силы и затухания в системе.
24.
Амплитуда и фаза вынужденныхколебаний:
h
A 2
2
0
f
m ( 0 ) 4
2
2 2
2
tg 2
2
2
2
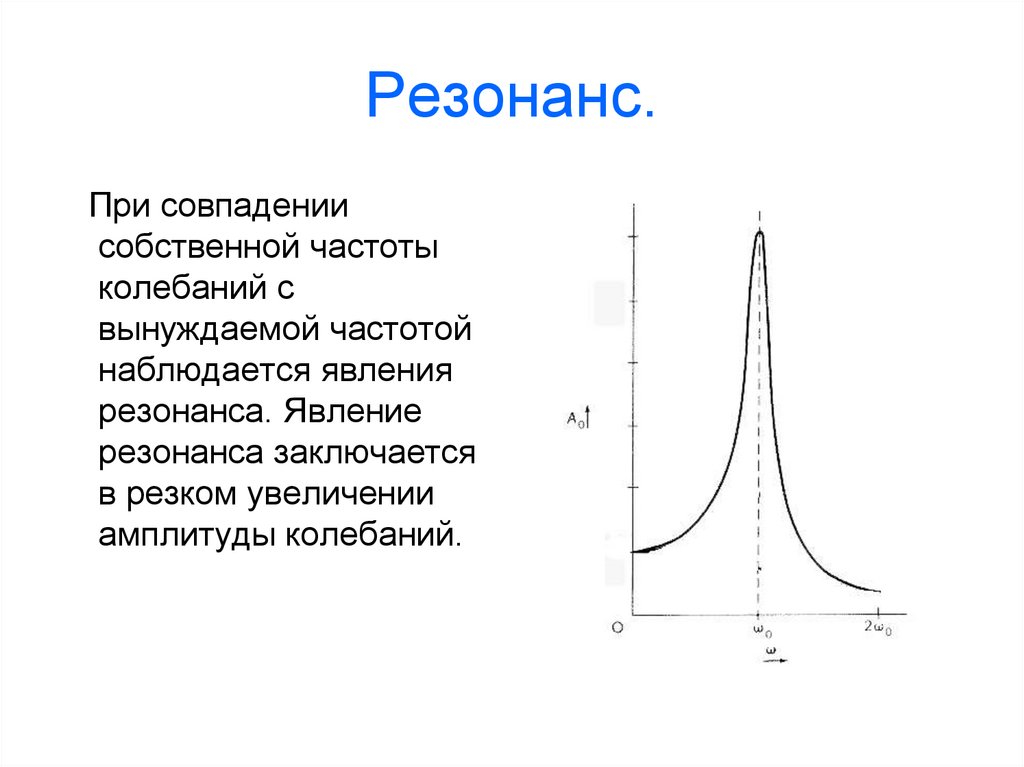
25. Резонанс.
При совпадениисобственной частоты
колебаний с
вынуждаемой частотой
наблюдается явления
резонанса. Явление
резонанса заключается
в резком увеличении
амплитуды колебаний.
26. Явление резонанса впервые описал
Галилиео Галилей (ита.Galileo Galilei; 15
февраля 1564, Пиза —
8 января 1642,
Арчетри) —
итальянский учёный
XVI—XVII
в.в., физик, создатель
научного метода,
создатель механики,
астроном.
27. Частота и амплитуда резонанса:
рез 0 2 02
Арез
2
f
2 0
2
2
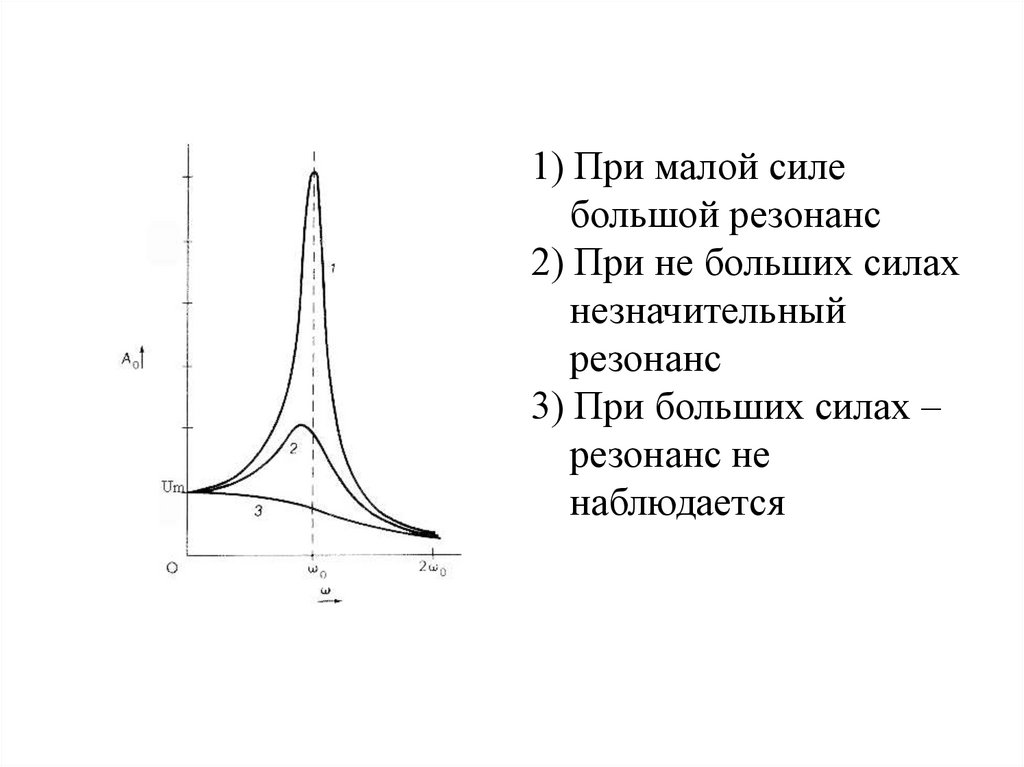
28. Зависимость амплитуды от силы трения
Эксперименты по изучению зависимостиамплитуды вынужденных колебаний от
значения сил трения показывают:
29.
1) При малой силебольшой резонанс
2) При не больших силах
незначительный
резонанс
3) При больших силах –
резонанс не
наблюдается




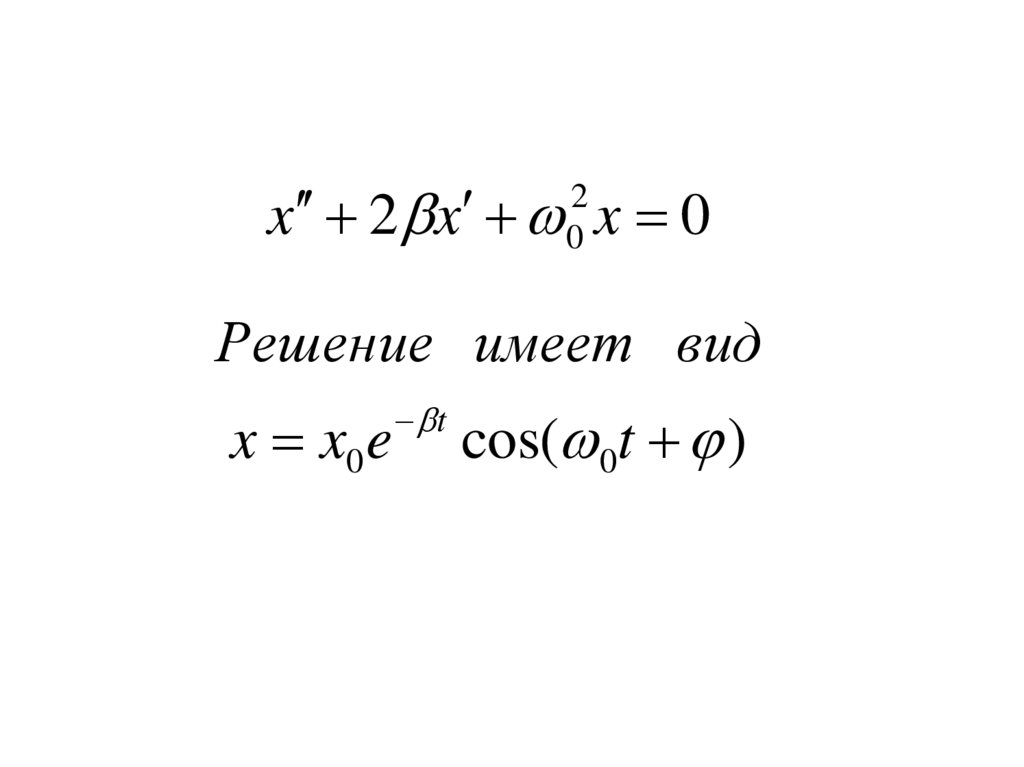




















 Физика
Физика








