Похожие презентации:
Стационарная теплопроводность. (Лекции 6-7)
1.
Лекции по ТТМОдоцент каф. Э6, ктн Рыжков С.В.
Э6
нергомашиностроение.
Лекция №6,7
СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ
•Интенсификация теплопередачи
•Теплопроводность при наличии внутренних источников теплоты
•Температурное поле полуограниченной пластины
•Температурное поле пористой пластины
2.
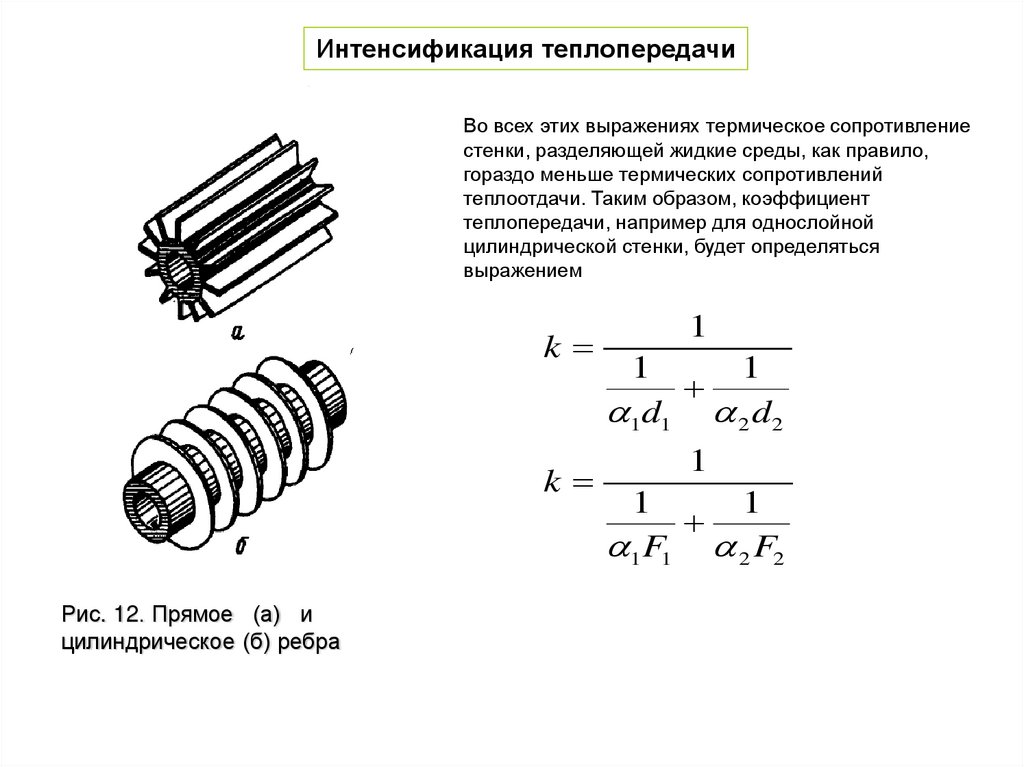
Интенсификация теплопередачиВо всех этих выражениях термическое сопротивление
стенки, разделяющей жидкие среды, как правило,
гораздо меньше термических сопротивлений
теплоотдачи. Таким образом, коэффициент
теплопередачи, например для однослойной
цилиндрической стенки, будет определяться
выражением
k
k
Рис. 12. Прямое (а) и
цилиндрическое (б) ребра
1
1
1
1d1 2 d2
1
1
1
1 F1 2 F2
3.
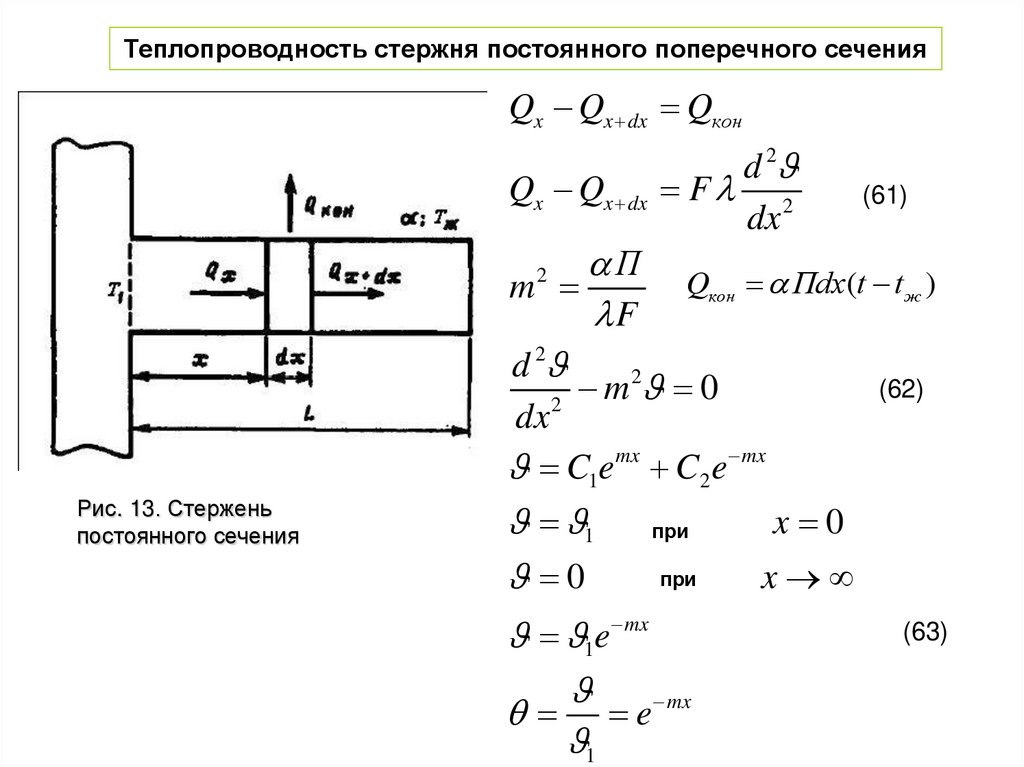
Теплопроводность стержня постоянного поперечного сеченияQx Qx dx Qкон
Qx Qx dx
d 2
F 2
dx
(61)
П Q Пdx(t t )
m
кон
ж
F
d 2
2
(62)
m
0
2
2
dx
C1e mx C2e mx
Рис. 13. Стержень
постоянного сечения
1
0
при
при
1e mx
e mx
1
x 0
x
(63)
4.
dQ F
dx
Fm 1 1 F
x 0
1
x 0
при
d
0 при
x L
dx
1e mL
1e mL
C1 mL mL ; C2 mL mL
e e
e e
ch m x L
em( L x ) e m( L x )
1
1
mL
mL
e e
ch mL
d
Q F
dx
(64)
Fm 1
x 0
sh mL
ch mL
(65)
1 F th mL (66)
5.
Температурное поле круглого ребра постоянной толщиныd 2 1 d 2
0
2
dr
r dr
2
2
2
d 2
d
d
d
m
2
m
,
m
2
2
dr
dz dr
dz
d 2 1 d
0 – уравнение Бесселя.
2
dz
z dz
C1 I 0 ( z ) C2 K 0 ( z )
1
0
при
r r1
при
r
I 0 (mr ) K1 (mr2 ) I1 (mr2 ) K 0 (mr )
1
I 0 (mr1 ) K1 (mr2 ) I1 (mr2 ) K 0 (mr1 )
(67)
z mr
(68)
(69)
(70)
6.
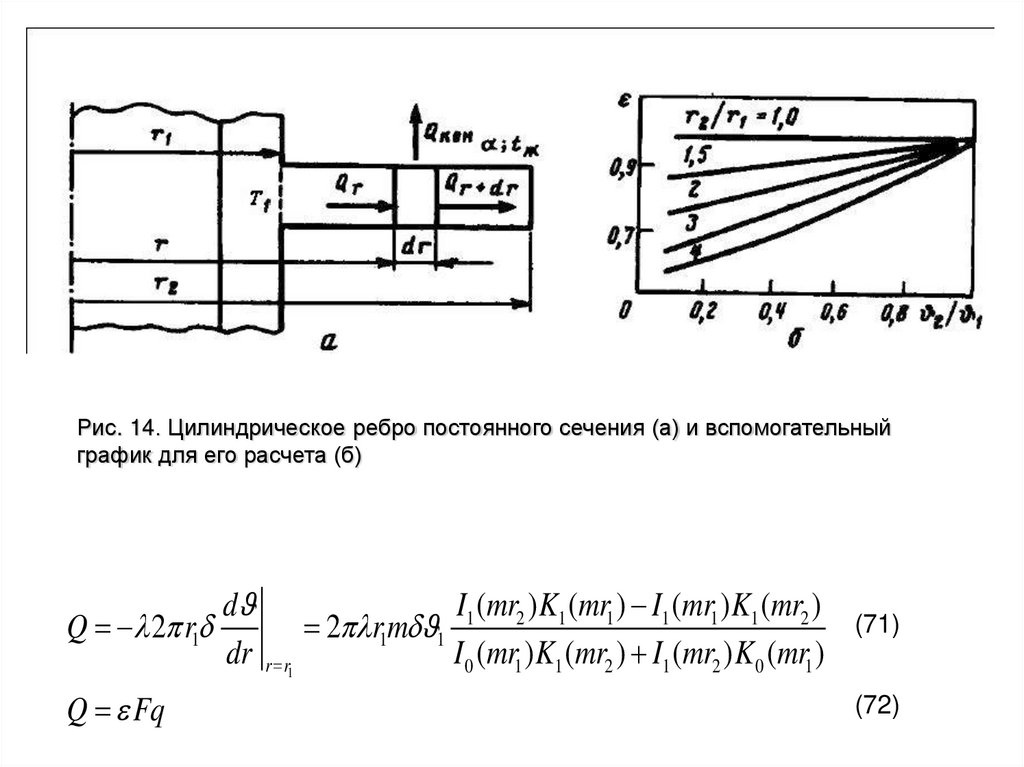
Рис. 14. Цилиндрическое ребро постоянного сечения (а) и вспомогательныйграфик для его расчета (б)
Q 2 r1
Q Fq
I (mr ) K (mr ) I (mr ) K (mr )
d
2 r1m 1 1 2 1 1 1 1 1 2
dr r r1
I 0 (mr1 ) K1 (mr2 ) I1 (mr2 ) K 0 (mr1 )
(71)
(72)
7.
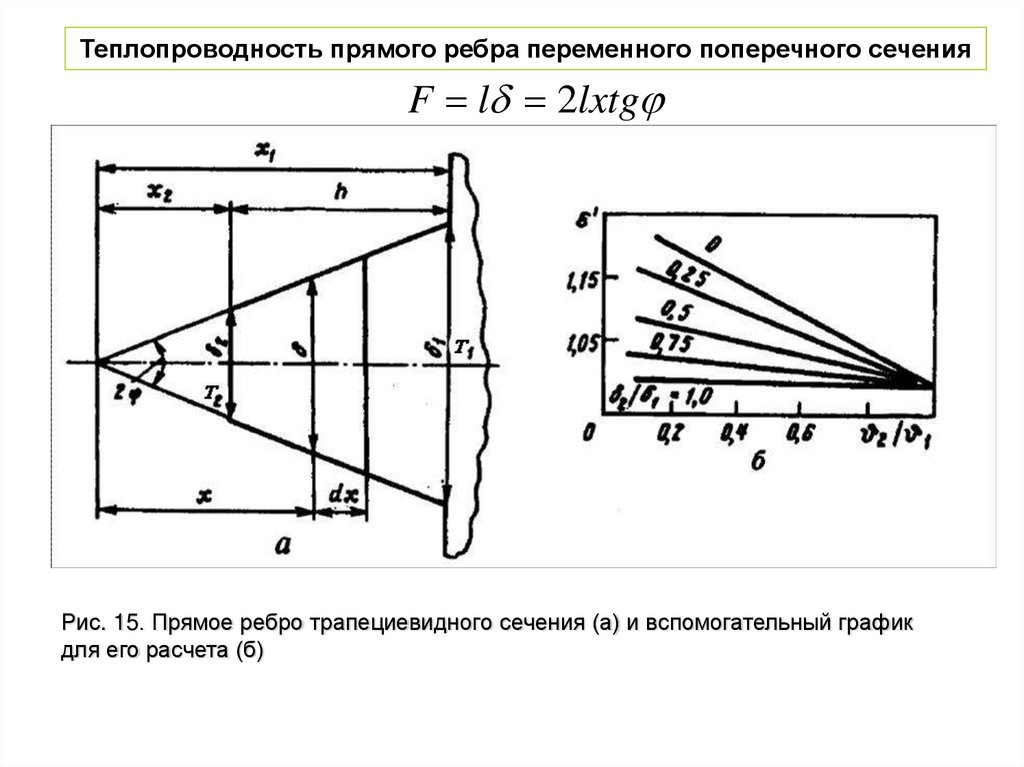
Теплопроводность прямого ребра переменного поперечного сеченияF l 2lxtg
Рис. 15. Прямое ребро трапециевидного сечения (а) и вспомогательный график
для его расчета (б)
8.
dd
F
dx
dx
d 2 1 d 1
0
2
dz
z dz z
x
z
tg
2l
(73)
– модифицированное уравнение Бесселя. (74)
C1 I 0 (2 z ) C2 K 0 (2 z )
(75)
Граничные условия
1
2
d
dx
при
x x1 ;
x x2 ;
0.
x x2
1
I 0 (2 z ) K1 (2 z2 ) I1 (2 z2 ) K 0 (2 z )
I 0 (2 z1 ) K1 (2 z2 ) I1 (2 z2 ) K 0 (2 z1 )
(76)
9.
dQ f1
dx
x x1
l 1 I1 (2 z1 ) K1 (2 z2 ) I1 (2 z2 ) K1 (2 z1 )
ztg I 0 (2 z1 ) K1 (2 z2 ) I1 (2 z2 ) K 0 (2 z1 )
Q ' qF '
(77)
( 78)
Теплопроводность при наличии внутренних источников теплоты.
Неограниченная пластина
Теплопроводность в однородной неограниченной пластине будем рассматривать при следующих
условиях: постоянство коэффициента теплопроводности и равномерное распределение тепловых
источников. Запишем дифференциальное уравнение для этих условий:
d 2T qV
0
2
dx
qV 2
T
x C1 x C2
2
(79)
(80)
10.
dTdx
dT
dx
1 (Tст1 Tж1 )
x 0
при
x 0
2 (Tст 2 Tж 2 )
x
при
x
T Tж
qV 2 / 2
T Tж 2 Tж1 Tж 2 k x k 2
Tж1 Tж 2
1
1
2
2
2
qV / 2 qV / 2 1 2 /
qV / 2
2
k 2
2
k 2
ж 1 x Bik 2 ж x 1
1
Bi2
1 Bi2
Bi2
2
Bik k
(81)
(82)
11.
2 / Bi 1 x2
q qV x
(83)
Q qV F
(84)
2
T Tст
1 x
2
qV / 2
(85)
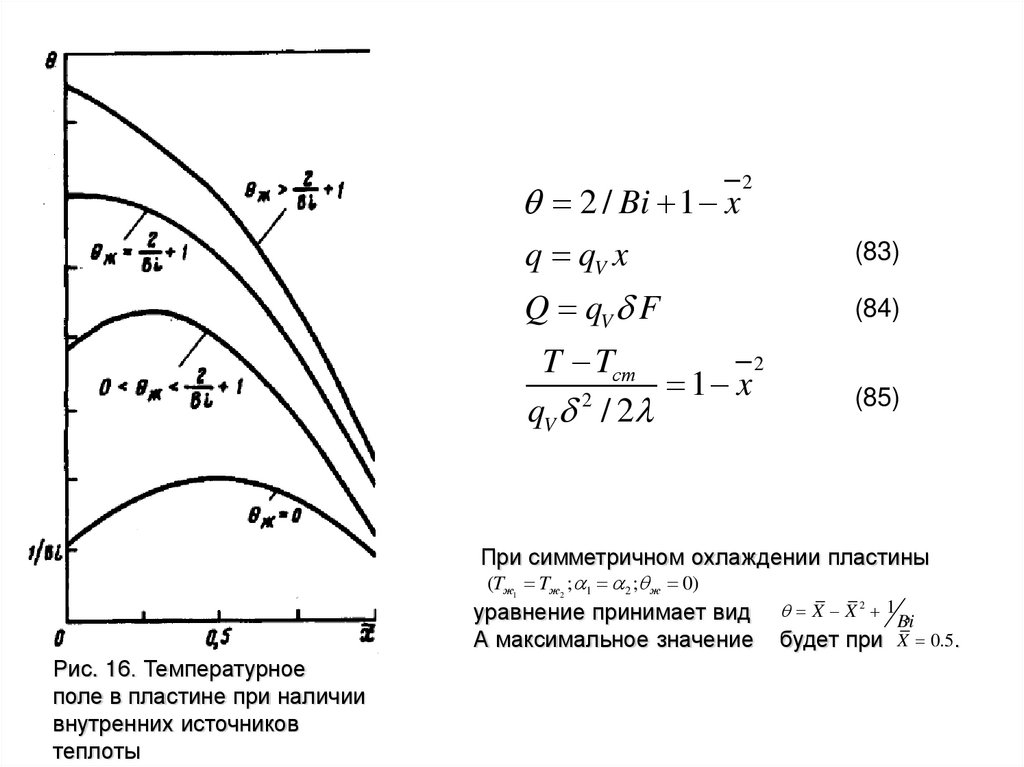
При симметричном охлаждении пластины
(Tж1 Tж2 ; 1 2 ; ж 0)
уравнение принимает вид
А максимальное значение
Рис. 16. Температурное
поле в пластине при наличии
внутренних источников
теплоты
X X 2 1 Bi,
будет при X 0.5.
12.
Цилиндрическая стенка1. Рассмотрим однородную цилиндрическую стенку (сплошной цилиндр) с равномерно
распределенными тепловыми источниками, у которой коэффициент теплопроводности λ не зависит
от температуры.
2
V
(86)
2
d T 1 dT q
0
dr
r dr
qV
rdz zdr rdr 0
dz qV r
C1r
dr 2
qV r 2
T
C1 ln r C2
4
qV r0 qV 2 2
T Tж
r0 r
2 4
qV r0
q Tст Tж
2
Граничные условия для (87) тогда
будут следующими:
(87)
(88)
(89)
dT
0
dr
r 0
dT
(Tст Tж )
dr r r0
13.
qV 2 2T Tст
r0 r
4
2. Цилиндрическая стенка (труба) с внутренним радиусом r1 и внешним r2 ,внутренняя
поверхность которого изолирована, а на внешней происходит конвективный теплообмен.
Граничные условия:
dT
0
dr
r r1
dT
Tcт2 Tж
dr r r2
qV
C1
r1
0
2
r1
qV r 21
C1
2
qV r22 qV r12
Tст2
ln r2 C2
4
2
14.
qV r2 qV r22 qV r12 qV r12C2 Tж
ln r2
2
4
2 r2
2
2
2
2
2
r1
r
qV r2
qV r2
r r
1
1 2ln
T Tж
2 r2 4 r2
r2 r2
2
r1
qV r2
1
Tст2 Tж
2 r2
2
r1
qV r2
1
q Tст 2 Tж
2 r2
3. Цилиндрическая стенка, теплота отводится через внутреннюю поверхность
трубы, наружная поверхность теплоизолирована.
Граничные условия
dT
0
dr
r r2
dT
Tcт1 Tж
dr r r1
(90)
(91)
(92)
15.
qV r22C1
2
qV r1 qV r12 qV r22 qV r22
C2 Tж
ln r2
2
4
2 r1
2
2
q r2
qV r1 r2
1 V 2
T Tж
2 r1
4
Tст1
2
qV r1 r2
1
Tж
2 r1
2
qV r1 r2
1
q
2 r1
2
2
r r1 r
2 ln
r1 r2 r2
(93)
(94)
(95)
4. Цилиндрическая стенка, теплота отводится конвективным теплообменом с обеих сторон трубы.
Для указанных условий очевидно, что имеется изотермическая поверхность с радиусом r0 ,
находящаяся между r1 и r2, где градиент температуры равен 0. Для части трубы между r1 и r0 ,
справедливы формулы (93) и (95),а для части трубы между r0 и r2 ,справедливы формулы (90) и
(92).Совокупность указанных выражений даёт возможность определить неизвестный радиус r0, а
затем величины T и q.
16.
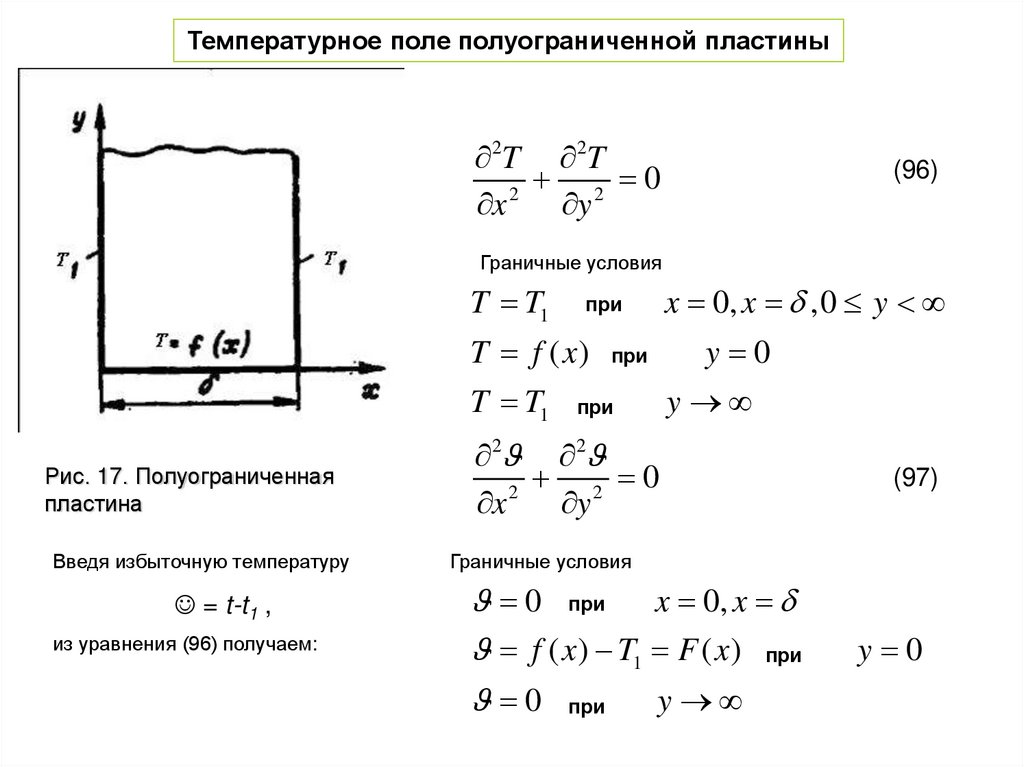
Температурное поле полуограниченной пластины2T 2T
2 0
2
x
y
(96)
Граничные условия
T T1
при
T f ( x)
T T1
Рис. 17. Полуограниченная
пластина
Введя избыточную температуру
= t-t1 ,
из уравнения (96) получаем:
при
при
x 0, x ,0 y
y 0
y
2 2
2 0
2
x
y
(97)
Граничные условия
0 при x 0, x
f ( x ) T1 F ( x ) при
0 при
y
y 0
17.
= (x) (y)Полагая, что
получаем:
и подставляя это выражение в (97),
''
''
const k 2
C1 cos( kx ) C2 sin( kx )
(98)
(99)
C3e ky C4 e ky
(100)
Ce ky sin( kx )
Cn sin( n x / )e n y /
(101)
n 1
n
F ( x ) Cn sin(
n 1
Cn
2
n
x)
n
F ( x )sin(
(102)
x ) dx
(103)
0
2
e
n 1
n
x
sin(
n
x ) F ( x )sin(
0
n
x ) dx
(104)
18.
иf (x) = t2
В частном случае, если
F (x) = t2-t1, то:
n
2
0 F ( x)sin( x)dx n T2 T1 0 m T2 T1
4
1
T2 T1 e
m 1 m
m
y
sin(
m
x)
(105)
Температурное поле пористой пластины
Пористые материалы находят широкое применение в современной технике, особенно при
использовании так называемого пористого охлаждения. В этом случае охлаждаемую деталь (лопатка
газовой турбины, сопло реактивного двигателя, камера сгорания и т.п.) выполняют из пористого
материала, через который прокачивается охлаждающая жидкость.
d 2Tc
c 2 1 P V Tc Tж 0
dx
d 2Tж
dTж
ж
T
T
Gc
V c
ж
pж
2
dx
dx
(106)
(107)
19.
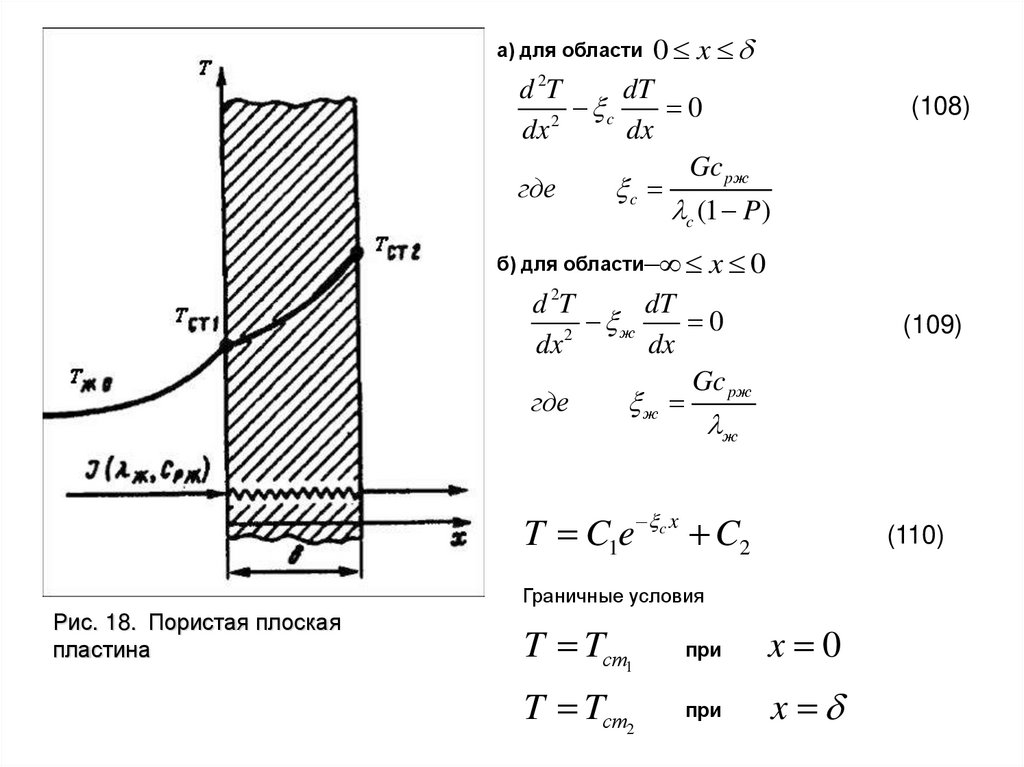
0 xd 2T
dT
0
c
2
dx
dx
Gc pж
где
c
c (1 P)
а) для области
б) для области
(108)
x 0
d 2T
dT
0
ж
2
dx
dx
Gc pж
где
ж
(109)
ж
T C1e c x C2
(110)
Граничные условия
Рис. 18. Пористая плоская
пластина
T Tст1
при
x 0
T Tст2
при
x
20.
(111)(112)
Граничные условия
при
при
(113)
(114)
21.
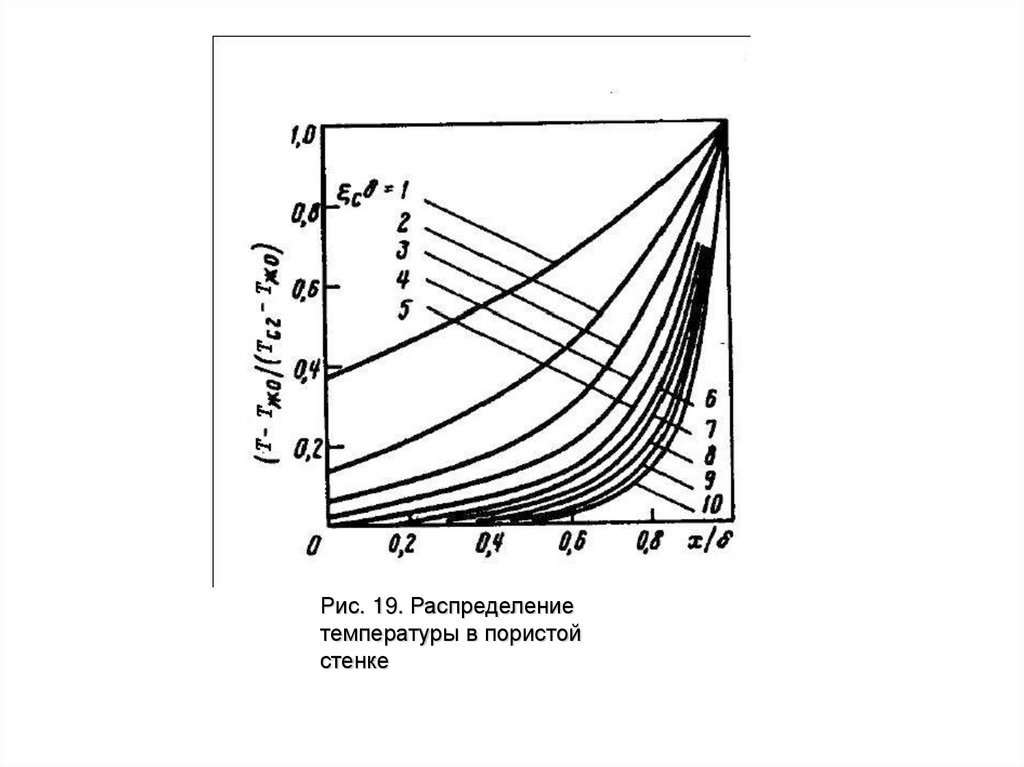
Рис. 19. Распределениетемпературы в пористой
стенке
22. Контрольные вопросы
Интенсификация теплопередачи
Теплопроводность стержня постоянного поперечного сечения
Температурное поле круглого ребра постоянной толщины
Теплопроводность прямого ребра переменного поперечного сечения
Теплопроводность при наличии внутренних источников теплоты
Цилиндрическая стенка
Температурное поле полуограниченной пластины
Температурное поле пористой пластины

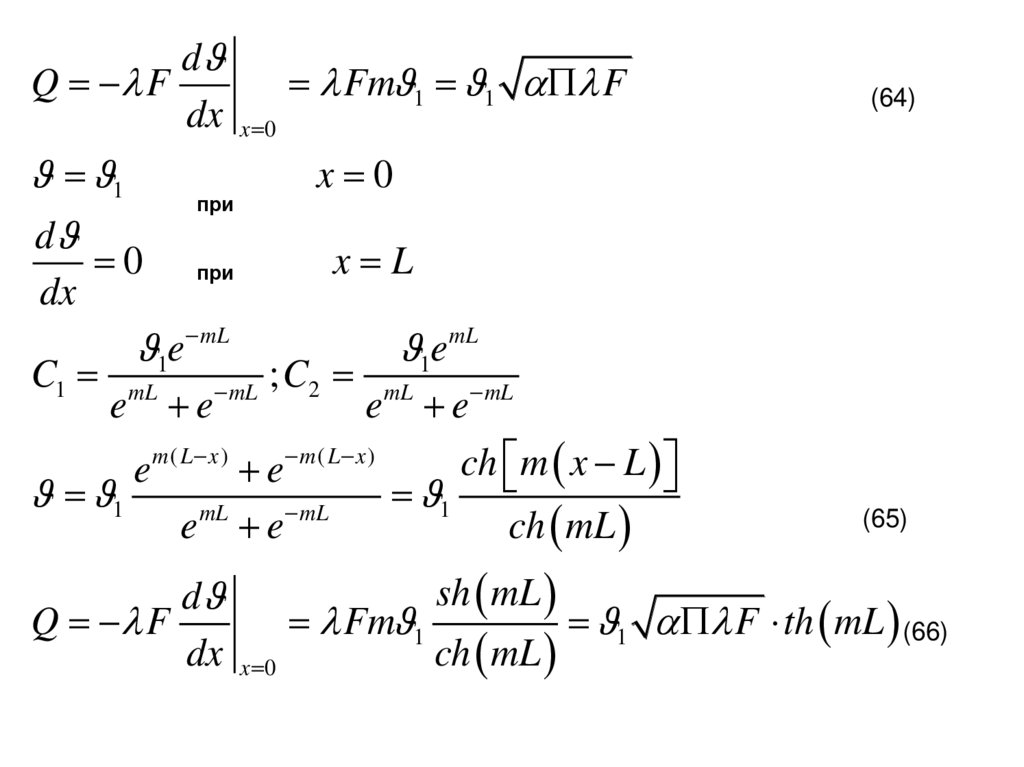



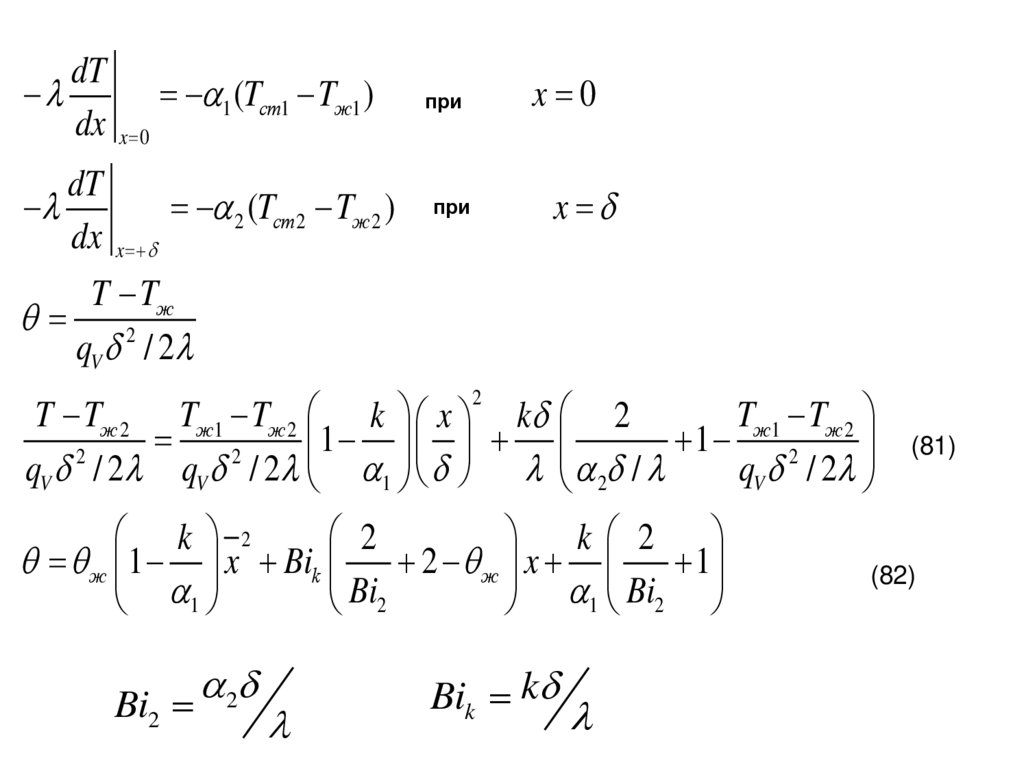








 Физика
Физика








