Техническая термодинамика. Теплопроводность при стационарном режиме. (Лекция 9)

1.

ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
ТЕПЛОПРОВОДНОСТЬ ПРИ
СТАЦИОНАРНОМ РЕЖИМЕ

2.

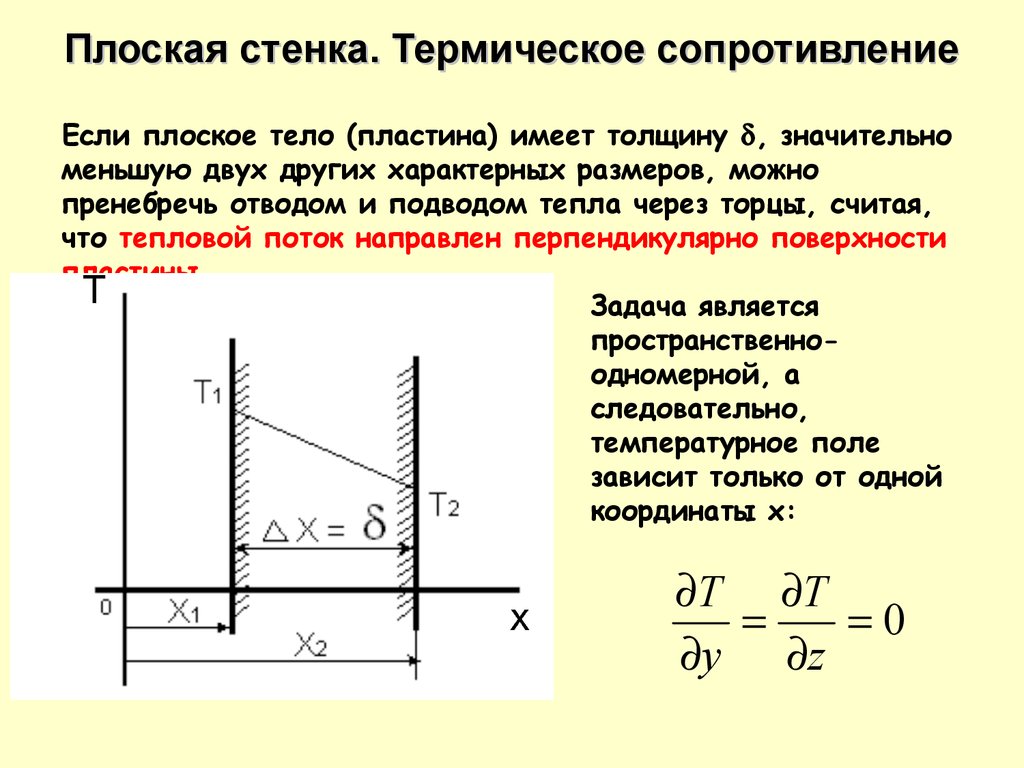
Плоская стенка. Термическое сопротивление
Если плоское тело (пластина) имеет толщину , значительно
меньшую двух других характерных размеров, можно
пренебречь отводом и подводом тепла через торцы, считая,
что тепловой поток направлен перпендикулярно поверхности
пластины
Задача является
пространственноодномерной, а
следовательно,
температурное поле
зависит только от одной
координаты х:
T T
0
y z

3.

Плоская стенка. Термическое сопротивление
При отсутствии объемного тепловыделения (qv = 0) и λ = const
уравнение теплопроводности
QV
T
a T
t
c
имеет вид:
d 2T
0
2
dx
Закон распределения температур по толщине стенки после
интегрирования:
T C1 x C 2
Здесь С1 и С2 – постоянные интегрирования. Видно, что
распределение температур в стенке соответствует линейному
закону. Изотермические поверхности представляют собой
плоскости, параллельные поверхностям стенки и нормальные к
оси х.

4.

Плоская стенка. Термическое сопротивление
Определим константы интегрирования исходя из граничных
условий первого рода:
при х = 0, Т = Т1
при х = , Т = Т2
Т1 – температура более нагретой стенки, Т2 – температура
более холодной стенки Т1 > Т2
Подставим условия в уравнение:
T1 C 2
Окончательно:
T2 C1 T1
T2 T1
T
x T1

5.

Плоская стенка. Термическое сопротивление
Для определения количества тепла, проходящего через
элемент стенки в единицу времени (dt = 1), воспользуемся
законом Фурье:
T
dQ
dS
x
Поскольку:
T2 T1
dT
C1
dx
Следовательно:
T2 T1
T1 T2
dQ
dS
dS
Для участка поверхности площадью S:
Q (T1 T2 ) S

6.

Плоская стенка. Термическое сопротивление
Обозначим Т1 – Т2 = Т, тогда
Q TS
Количество тепла, проходящее через единицу поверхности в
единицу времени, определяется соотношением:
Q
q T
S
Отношение λ/ обычно называют тепловой проводимостью
стенки, а обратная величина / λ – сопротивлением
теплопроводности стенки.

7.

Плоская стенка. Теплопроводность при
объемном тепловыделении
К объемному тепловыделению можно отнести следующие
явления: конденсация, нагревание, ядерные реакции и др.
Основное уравнение будет иметь вид:
d 2T QV
a 2
0
dx
c
Принимая во внимание, что a = (cρ):
d 2T QV
0
2
dx

8.

Плоская стенка. Теплопроводность при
объемном тепловыделении
Считая QV = const, после первого интегрирования получаем:
QV
dT
x C1
dx
После второго:
2
QV x
f ( x)
C1 x C2
2
Постоянные интегрирования находятся из граничных условий

9.

Плоская стенка. Теплопроводность при
объемном тепловыделении
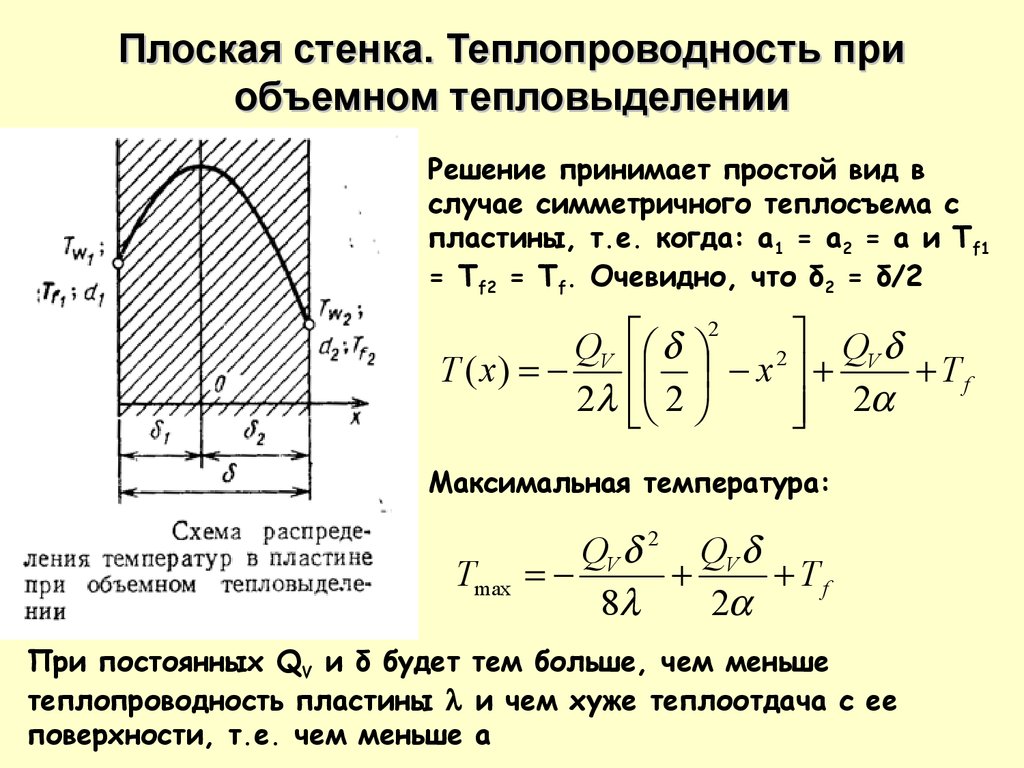
Решение принимает простой вид в
случае симметричного теплосъема с
пластины, т.е. когда: a1 = a2 = a и Tf1
= Tf2 = Tf. Очевидно, что δ2 = δ/2
QV
T ( x)
2
2
QV
2
Tf
x
2
2
Максимальная температура:
Tmax
QV 2 QV
Tf
8
2
При постоянных QV и δ будет тем больше, чем меньше
теплопроводность пластины и чем хуже теплоотдача с ее
поверхности, т.е. чем меньше а

10.

Плоская стенка. Теплопроводность при
объемном тепловыделении
Температура на поверхности пластины x = δ/2:
QV
Tw
Tf
2
также растет с ухудшением теплоотдачи.

11.

Теплопередача между двумя жидкостями через
разделяющую их стенку. Коэффициент теплопередачи
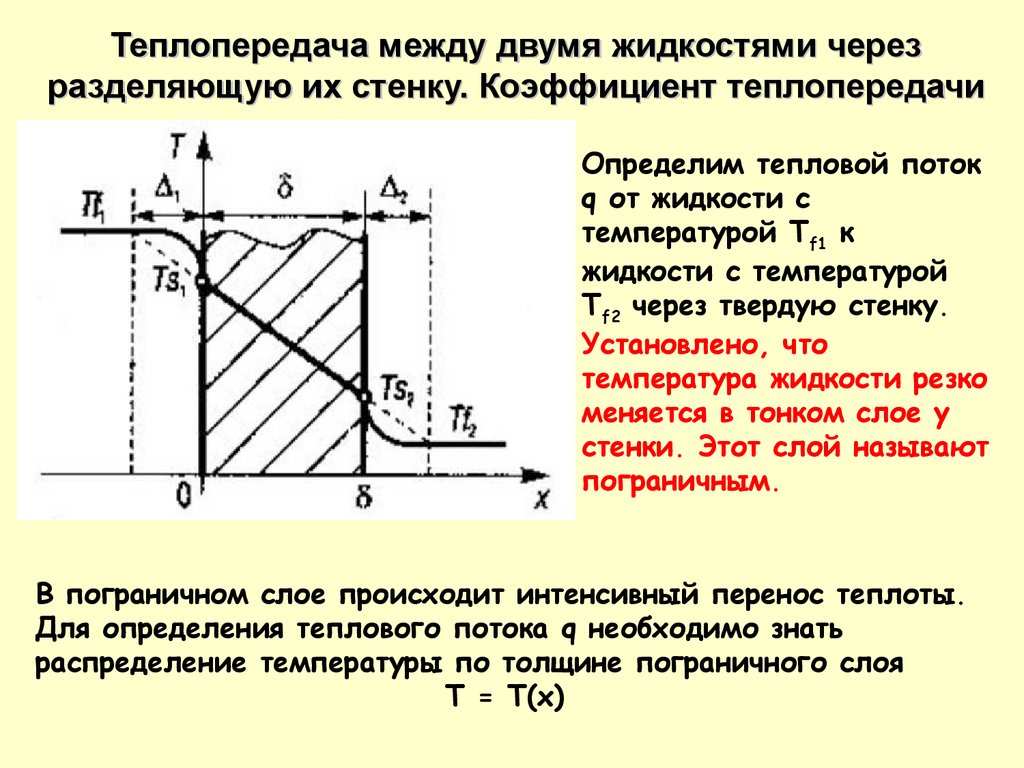
Определим тепловой поток
q от жидкости с
температурой Tf1 к
жидкости с температурой
Tf2 через твердую стенку.
Установлено, что
температура жидкости резко
меняется в тонком слое у
стенки. Этот слой называют
пограничным.
В пограничном слое происходит интенсивный перенос теплоты.
Для определения теплового потока q необходимо знать
распределение температуры по толщине пограничного слоя
T = T(x)

12.

Теплопередача между двумя жидкостями через
разделяющую их стенку. Коэффициент теплопередачи
Обычно величину q определяют по формуле Ньютона:
q (T f Ts )
α – коэффициент теплоотдачи. Данная формула удобнее чем:
q gradT
Т.к. коэффициент α проще определить экспериментально, чем
зависимость T = T(x)
Таким образом, тепловой поток на левой стенке: q = α1(Tf1 – Ts1)
На правой стенке: q = α2(Tf2 – Ts2)
Через стенку: q = λ/ (Ts1 – Ts2)

13.

Теплопередача между двумя жидкостями через
разделяющую их стенку. Коэффициент теплопередачи
После преобразований получаем:
q
T f 1 Ts 1
1
q
Ts 2 T f 2
2
q Ts 1 Ts 2
Складываем почленно левые и правые части:
1
1
T f 1 T f 2
q
1 2
q k (T f 1 T f 2 )
1
k
1/ 1 / 1 / 2
k – коэффициент теплопередачи (Вт/м2К), а обратная величина
R = 1/k – полное термическое сопротивление (м2К/Вт)

14. Пусть многослойная стенка состоит из n плотно прилегающих слоев, коэффициенты теплопроводности которых равны λ1..λn, а толщины 1..n.

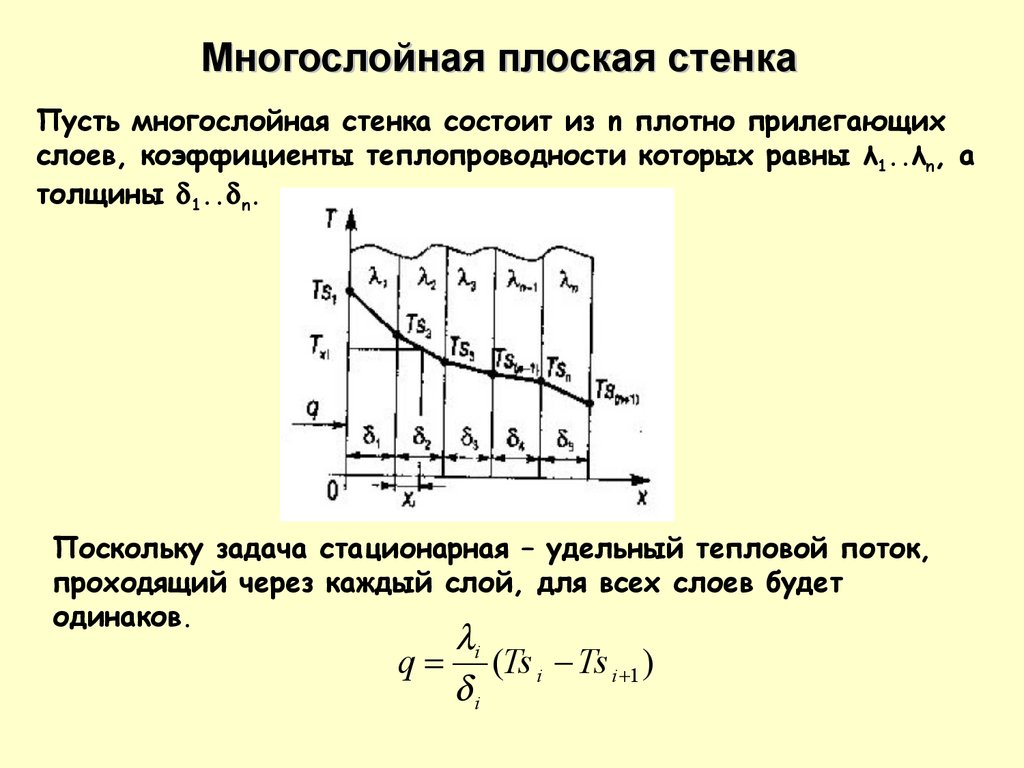
Многослойная плоская стенка
Пусть многослойная стенка состоит из n плотно прилегающих
слоев, коэффициенты теплопроводности которых равны λ1..λn, а
толщины 1.. n.
Поскольку задача стационарная – удельный тепловой поток,
проходящий через каждый слой, для всех слоев будет
одинаков.
i
q (Ts i Ts i 1 )
i

15.

Многослойная плоская стенка
Перепишем эти выражения в виде:
i
q Ts i Ts i 1
i
1 2
Произведем почленное сложение: q
... n
n
1 2
Отсюда:
q
Ts 1 Ts n 1
i
i
Сумма в знаменателе – суммарное сопротивление
теплопроводности многослойной стенки.
Ts 1 Ts n 1

16.

Многослойная плоская стенка
Иногда вводят в рассмотрение эквивалентный коэффициент
теплопроводности λэкв, который равен коэффициенту
теплопроводности фиктивной однослойной стенки, равной толщине
многослойной и при условии, что разности температур на границах
однослойной и многослойной стенок одинаковы, а количество
тепла, проходящее через них в единицу времени, совпадает
экв
q
(Ts 1 Ts n 1 )
i
экв
/
i
i
i
Эквивалентный коэффициент теплопроводности позволяет
сравнивать теплопроводящие свойства многослойной стенки,
составленной из разнородных материалов, с однослойной
стенкой, выполненной из однородного материала.
Внутри слоя распределение температуры описывается как:
xi
Txi Ts i q
i

17.

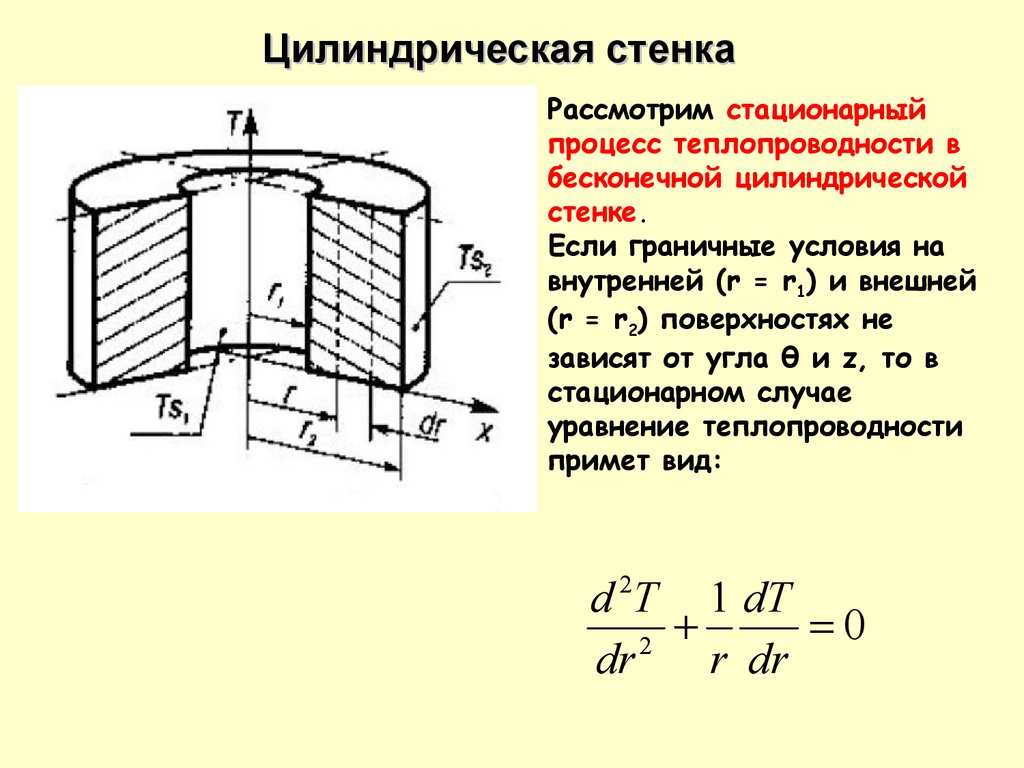
Цилиндрическая стенка
Рассмотрим стационарный
процесс теплопроводности в
бесконечной цилиндрической
стенке.
Если граничные условия на
внутренней (r = r1) и внешней
(r = r2) поверхностях не
зависят от угла θ и z, то в
стационарном случае
уравнение теплопроводности
примет вид:
d 2T 1 dT
0
2
dr
r dr

18.

Цилиндрическая стенка
Пусть заданы граничные условия первого рода:
при r = r1, T = Ts1
при r = r2, T = Ts2
Определим распределение температуры по толщине стенки:
1 d dT
r
0
r dr dr
После первого интегрирования:
После второго интегрирования:
dT
r
C1
dr
dT C1
dr
r
T (r ) C1 ln r C 2

19.

Цилиндрическая стенка
Находим постоянные интегрирования:
Ts 2 Ts 1
C1
r
ln 2
r1
C 2 Ts 2
Ts 2 Ts 1
Ts ln r Ts 2 ln r1
ln r2 1 2
r2
r2
ln
ln
r1
r1
Общее решение:
r2
r
Ts 2 ln Ts 1 ln
Ts 2 Ts 1
Ts 1 ln r2 Ts 2 ln r1
r1
r
T (r )
ln r
r2
r2
r2
ln
ln
ln
r1
r1
r1

20.

Цилиндрическая стенка
Анализ формулы показывает:
1) Удельный тепловой поток в цилиндрической стенке q = -λdT/dr
непостоянен по толщине и убывает к внешней поверхности
трубы (dT/dr ~ 1/r). Это связано с тем, что в стационарных
условиях должен быть постоянным полный тепловой поток,
проходящий через участок цилиндрической трубы равный qS.
Поскольку S увеличивается с радиусом, то тепловой поток
должен убывать.
2) Температура по толщине цилиндрической стенки изменяется
нелинейно – по логарифмическому закону
Количество тепла, проходящее через участок цилиндрической
трубы длиной L в единицу времени не зависит от r:
Ts 1 Ts 2
Ts 1 Ts 2
T
Q
2 rL
2 rL
2 L
r
r
r
r ln 2
ln 2
r1
r1

21.

Контактное термическое сопротивление
Идеально плотный контакт между отдельными слоями
многослойной стенки получается, если один из слоев
наносят на другой в жидком состоянии или в виде текучего
раствора. Твердые тела касаются друг друга вершинами
профилей шероховатостей. Площадь контакта вершин
пренебрежимо мала, и весь тепловой поток идет через
воздушный зазор. Это создает дополнительное (контактное)
термическое сопротивление Rк (кг*К/Дж). Его можно
приближенно оценить, если принять, что толщина зазора
между соприкасающимися телами в среднем вдвое больше
максимального расстояния макс между впадинами.

22.

Контактное термическое сопротивление
При контакте двух пластин с шероховатостью поверхности 5-го
класса (после чистовой обточки, строгания, фрезерования)
макс ≈ 0,03 мм и в воздухе комнатной температуры
1.5 10 5
3
Rk
0
.
58
10
2.59 10 2
Это эквивалентно термическому сопротивлению стали толщиной
около 30 мм.
Для
уменьшения
контактного
сопротивления
необходимо
заполнять зазоры каким-либо материалом с более высокой, чем
у воздуха, теплопроводностью, например спаять или склеить
поверхности