Похожие презентации:
Интеграл. Первообразная
1. Восхождение на вершину «Интеграл».
Преподавательматематики
Карачарова Е.Н.
2.
• Всякое учениеистинно в том,
что оно
утверждает, и
ложно в том, что
оно отрицает или
исключает.
Фрид Вильгельм Лейбниц
3.
Разминка перед восхождением.Найти первообразную для каждой функции.
f (x)
k
F (x)
kx
f (x)
x
F (x)
x2
2
х
1
n
х
x n 1
n 1
2 х
e
x
e
x
1
x
ln x
sin x
cos x
1
x2
1
x
cos x
sin x
4. Проверка снаряжения
1) f x x 42) f x x 5 x 7
3) f x 3x 2 x
4) f x x 5 x 3 5
6) f x 4 sin x
7) f x 2 cos x 4 x 9
1
8) f x
x 2
x
3
3
9) f x 3 sin x
x
x 4
10)5 cos x x 3 6 x 5
1)F(x) = 4x3+c
2) F(x) = 5x4+ 7x6+c
3) F(x) = 6x+1+c
4) F(x) = 1+15x2+c
6) F(x) = -cos x +c
7) F(x) = 2sin x- 9x8 +c
8) F(x) =2 +1+с
9. F(x) = -3cos x +6
+
х2+c
10) F(x) = 5sin x- 3x2+6 +c
5. АЛГОРИТМ РЕШЕНИЕ ЗАДАЧ
1. Построить графики данных линий.Определить искомую фигуру.
2. Найти пределы интегрирования.
3. Записать площадь искомой фигуры с
помощью определенного интеграла.
4. Вычислить полученный интеграл.
6.
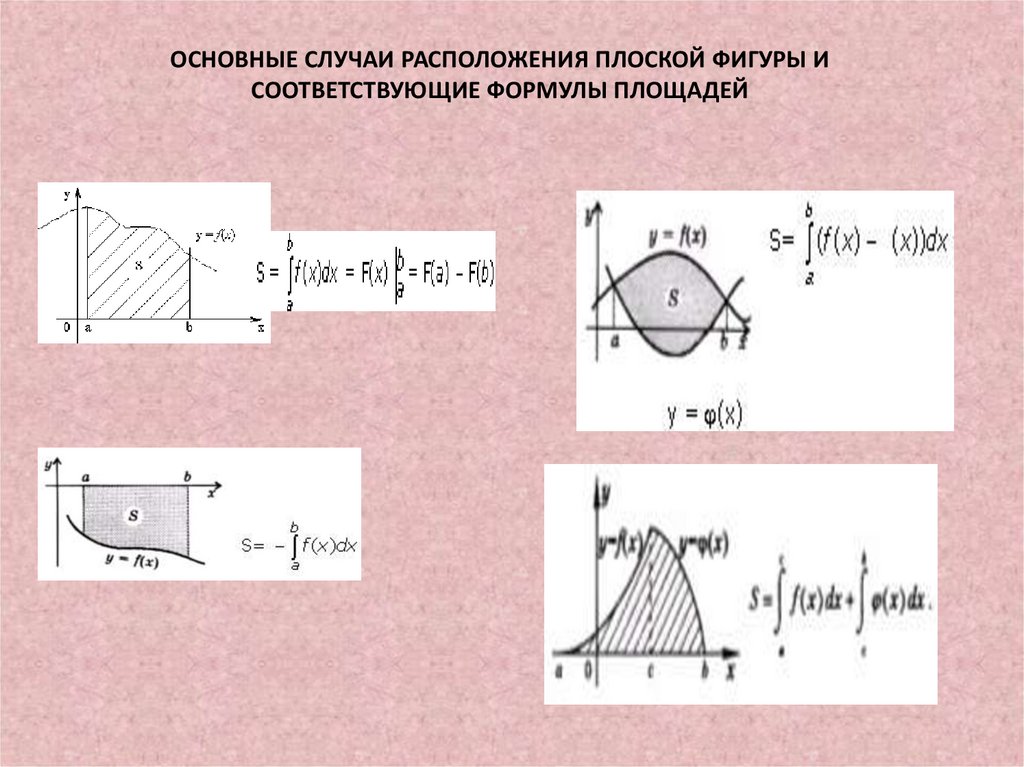
ОСНОВНЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ПЛОСКОЙ ФИГУРЫ ИСООТВЕТСТВУЮЩИЕ ФОРМУЛЫ ПЛОЩАДЕЙ
7. Начало пути "связки А" и "связки В". Найти площадь фигуры, ограниченной линиями.
Начало пути "связки А" и "связки В".Найти площадь фигуры, ограниченной
линиями.
I вариант
у=х2+1,
у=3-х
II вариант
У = (х+1)2,у=1-х
Ось ох
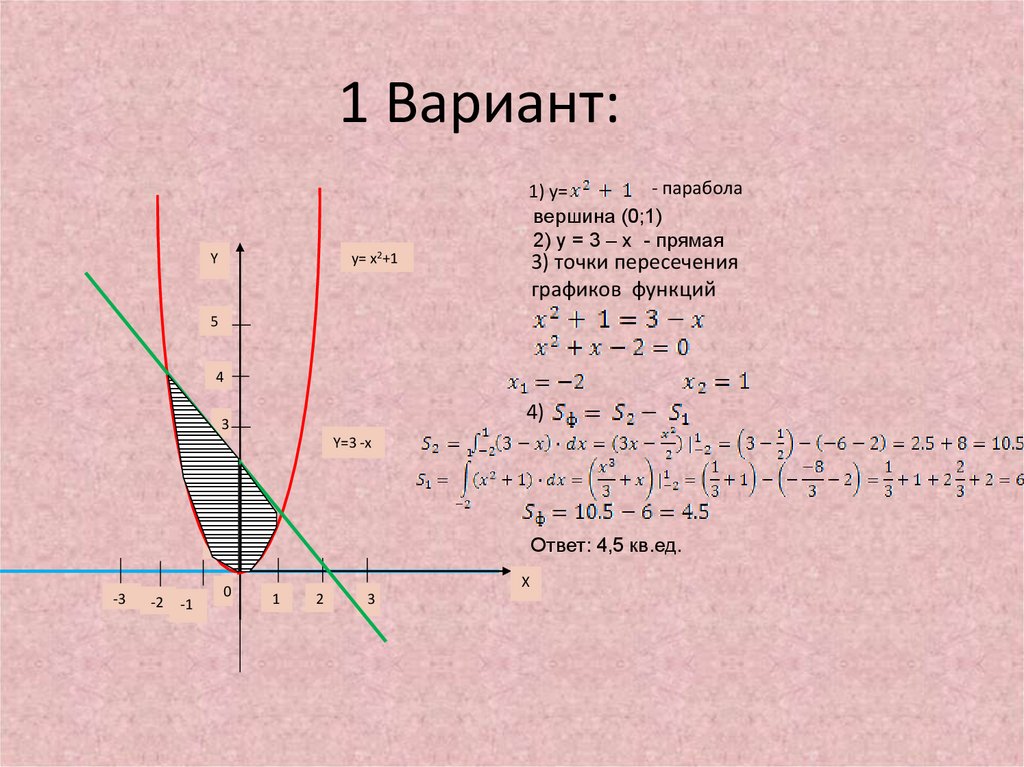
8. 1 Вариант:
y= x2+1Y
- парабола
1) y=
вершина (0;1)
2) y = 3 – x - прямая
3) точки пересечения
графиков функций
5
4
4)
3
Y=3 -x
2
1
Ответ: 4,5 кв.ед.
-3
-2
-1
0
X
1
2
3
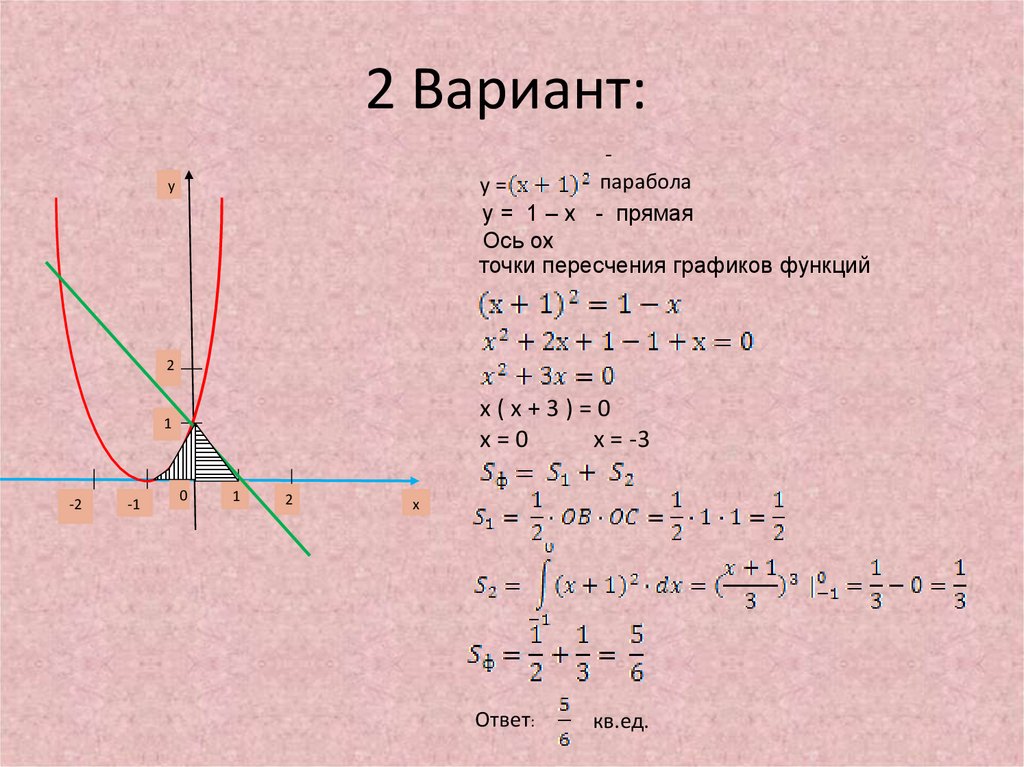
9. 2 Вариант:
параболаy=
y = 1 – x - прямая
Ось ox
точки переcчения графиков функций
y
2
x(x+3)=0
x=0
x = -3
1
-2
-1
0
1
2
x
Ответ:
кв.ед.
10. Штурм горы.
11. Решение примеров.
12.
Привал .К О Н Т
Д
К
П Л
И Н Т Е Г
Л Е Й Б
С Т
Ф У Н К Ц И
П
Е
Р
В
О
О
Б
Р
А
З
Н
А
Я
Р
Д
О
Е
Р
Щ
Я
И
Л
Н
Е
А
М
Н
Ь
А
Н
Д
А
И
Н
Д
Ь
Ь
А Л
А Ч Е Т
И Ц
Д И Я
Я
Ц А
А Я
Ц А Т Ь
13. Немного истории
«Интеграл» - латинское словоintegro – “восстанавливать”
или integer – “целый”.
Одно из основных понятий
математического анализа,
возникшее в связи
потребностью измерять
площади, объемы, отыскивать
функции по их производным.
Впервые это слово употребил
в печати швецкий ученый Я.
Бернулли (1690 г.).
14. Немного истории
15.
Площадь фигурыОбъем тела вращения
Работа электрического заряда
Работа переменной силы
Центр масс
Формула энергии заряженного конденсатора






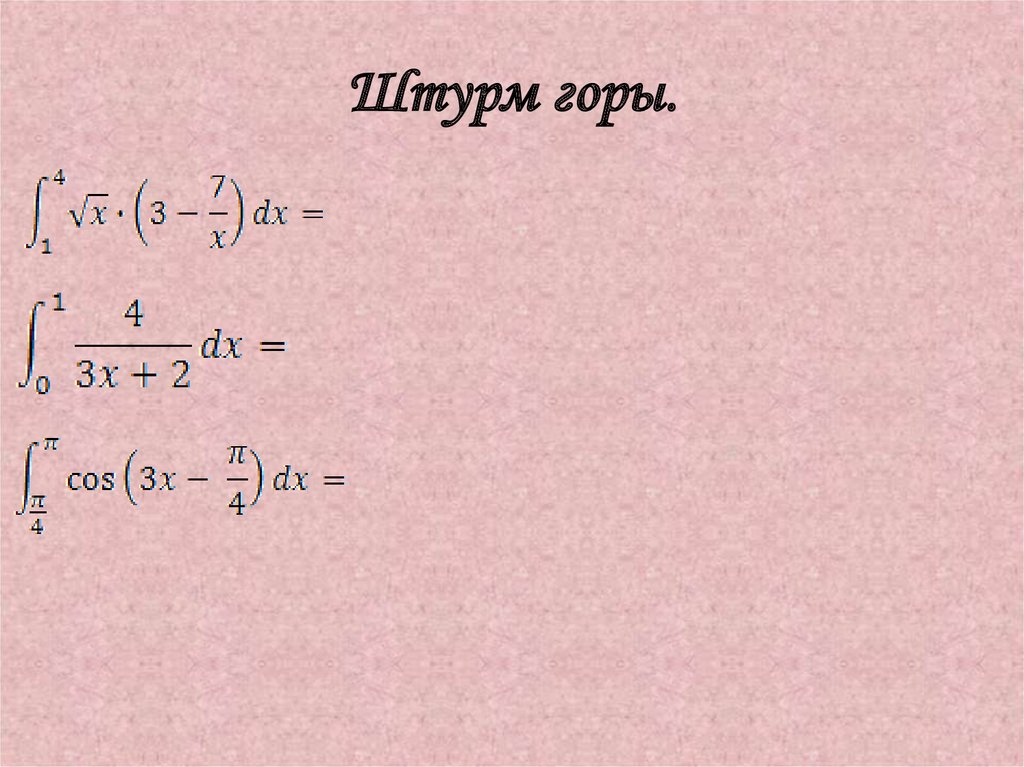






 Математика
Математика








