Постоянный электрический ток

1.

Постоянный
электрический
ток

2.

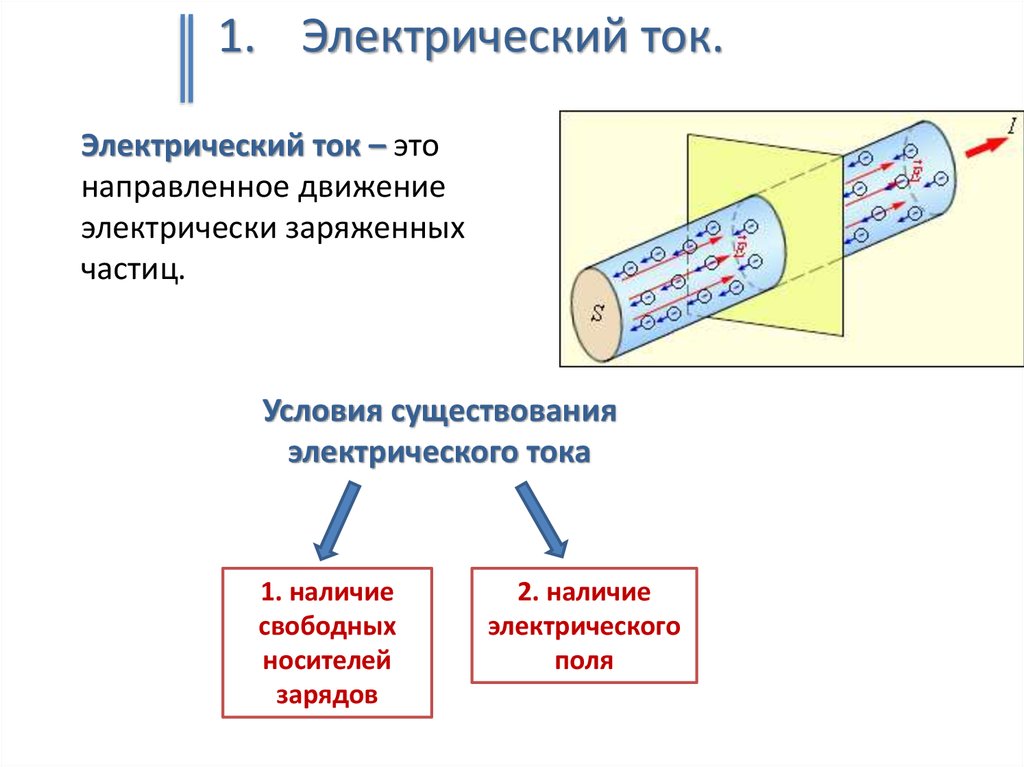
1. Электрический ток.
Электрический ток – это
направленное движение
электрически заряженных
частиц.
Условия существования
электрического тока
1. наличие
свободных
носителей
зарядов
2. наличие
электрического
поля

3.

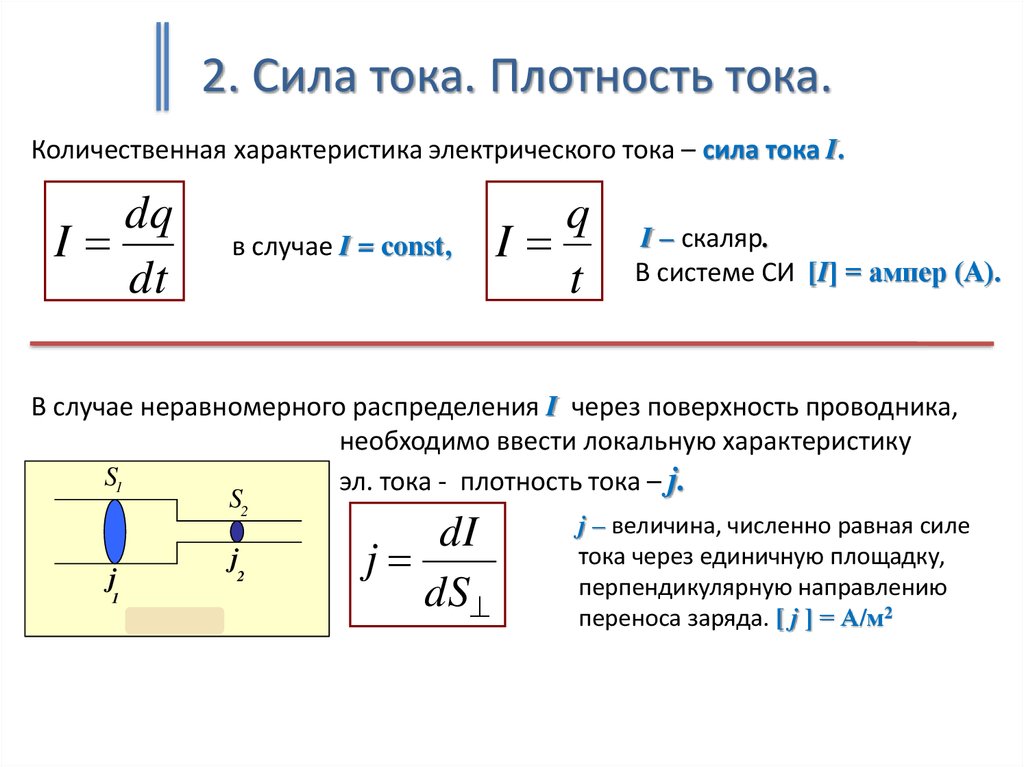
2. Сила тока. Плотность тока.
Количественная характеристика электрического тока – сила тока I.
dq
I
dt
в случае I = const,
q
I
t
I – скаляр.
В системе СИ [I] = ампер (А).
В случае неравномерного распределения I через поверхность проводника,
необходимо ввести локальную характеристику
S1
эл. тока - плотность тока – j.
S2
j
j
2
1
Рис. 57.3.
dI
j
dS
j – величина, численно равная силе
тока через единичную площадку,
перпендикулярную направлению
переноса заряда. [ j ] = А/м2

4.

СВЯЗЬ ПЛОТНОСТИ ТОКА С ПАРАМЕТРАМИ ЗАРЯЖЕННЫХ ЧАСТИЦ,
УЧАСТВУЮЩИХ В ПЕРЕНОСЕ.
u dt
u
n
dS
u
- средняя скорость упорядоченного движения
носителя заряда
n
- концентрация носителей заряда в веществе
dI
dq qe dN
j
dI
dS
dt
dt
j qe n u
qe n u dtdS
dt
qe n u
- вектор плотности тока,
его направление совпадает со скоростью
упорядоченного
движения положительно заряженных носителей (частиц)

5.

3. Уравнение непрерывности.
I j dS
dI j dS
S
- поток плотности тока через
выделенную поверхность
dq
d
Ф j j dS
dV
dt
dt V
S
j dS t dV j dS divj dV т. О Г
S
V
S
V
divj
t
- т. Гаусса. Спец название - уравнение непрерывности
для
плотности тока. Свидетельствует: источниками поля j
являются те точки среды, в которых происходит убыль
Для постоянного тока
0
t
divj 0

6.

4. Электродвижущая сила (ЭДС). Напряжение
Необходимое условие существования постоянного тока –
наличие ЭДС
Сторонние силы – силы
2
2
неэлектростатического
*
*
*
A12 F dl q E dl
происхождения.
1
1
Работа этих сил по перемещению
заряда А*
*
E - напряженность поля сторонних сил
12
*
A12 2 *
E dl
q
*
эл
A12 A12
A12
q( 1 2 ) q 12
A12
U12
q
( 1 2 ) 12
1

7.

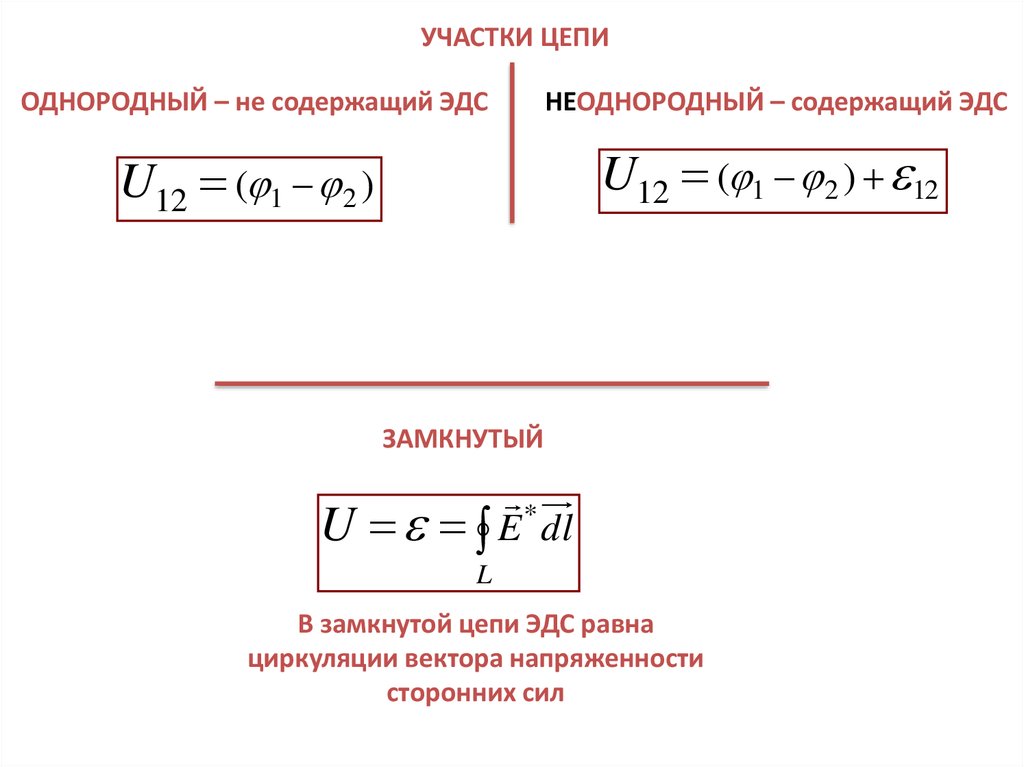
УЧАСТКИ ЦЕПИ
ОДНОРОДНЫЙ – не содержащий ЭДС
НЕОДНОРОДНЫЙ – содержащий ЭДС
U12 ( 1 2 )
U12 ( 1 2 ) 12
ЗАМКНУТЫЙ
U
*
E dl
L
В замкнутой цепи ЭДС равна
циркуляции вектора напряженности
сторонних сил

8.

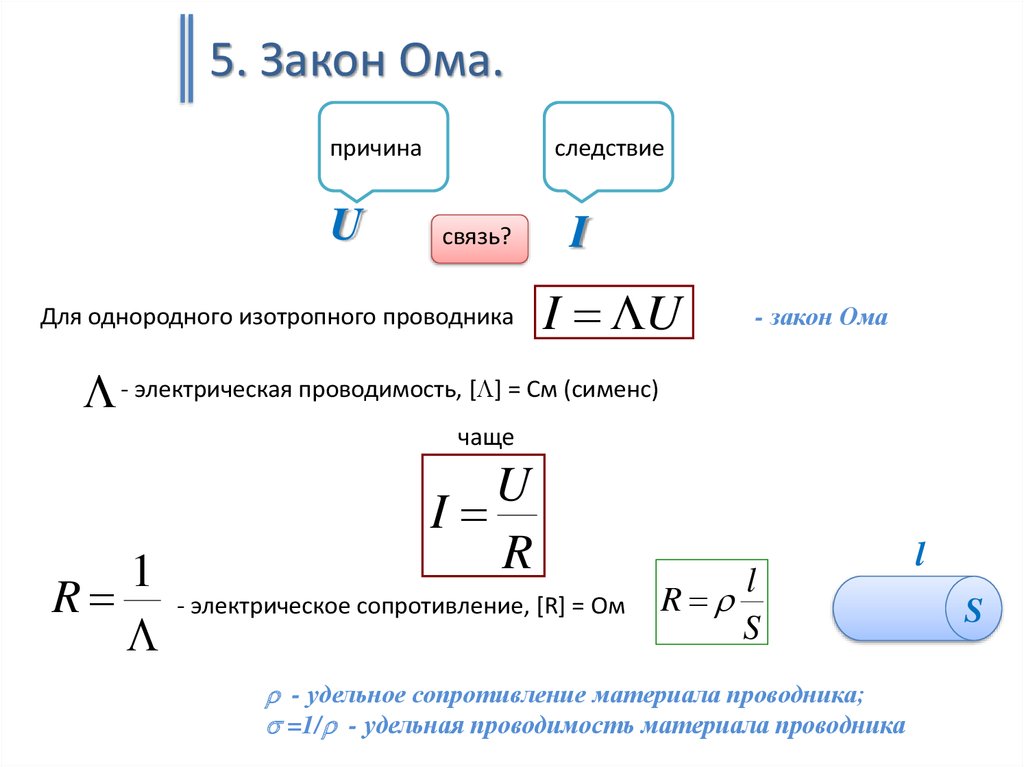
5. Закон Ома.
причина
U
следствие
связь?
Для однородного изотропного проводника
I
I U
- закон Ома
- электрическая проводимость, [ ] = Cм (сименс)
чаще
1
R
U
I
R
- электрическое сопротивление, [R] = Ом
l
R
S
- удельное сопротивление материала проводника;
=1/ - удельная проводимость материала проводника
l
S

9.

Закон Ома для УЧАСТКОВ ЦЕПИ
1. ОДНОРОДНОГО
1
I
R
2. НЕОДНОРОДНОГО
2
1
U12 1 2
I
R
R
+, r
I
-
R
I
1 2
R r
3. ЗАМКНУТОЙ ЦЕПИ
R
I
+, r
-
I
R r
2

10.

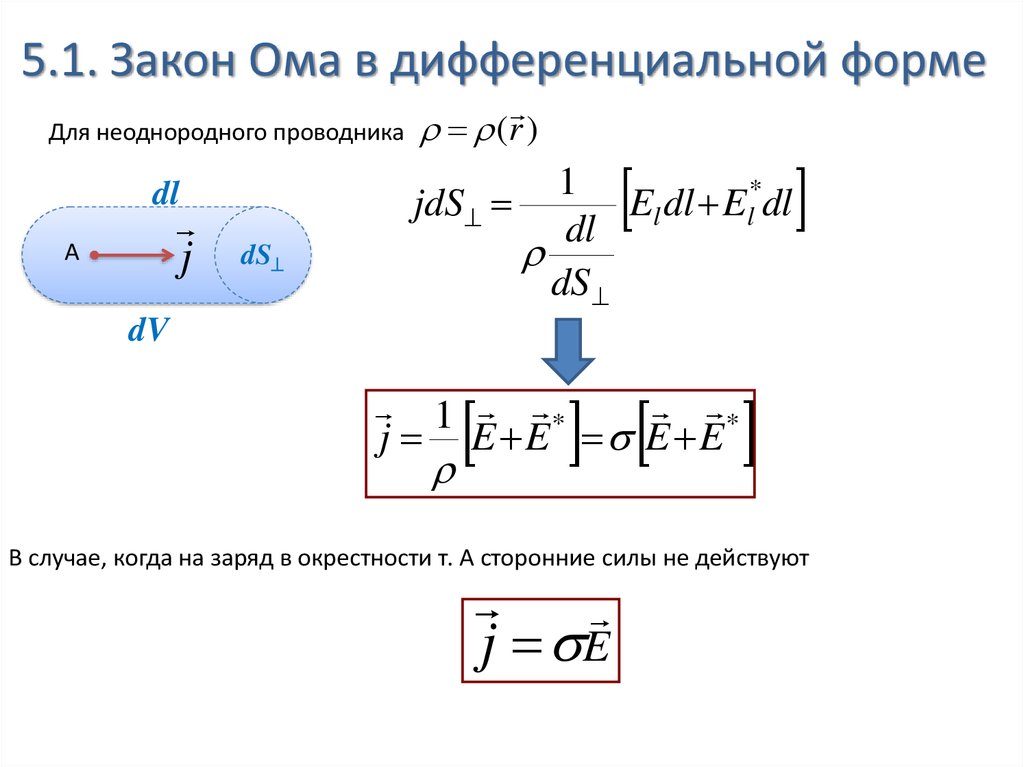
5.1. Закон Ома в дифференциальной форме
Для неоднородного проводника
dl
j
A
dS
(r )
1
*
jdS
El dl El dl
dl
dS
dV
*
1 *
j E E E E
В случае, когда на заряд в окрестности т. А сторонние силы не действуют
j E

11.

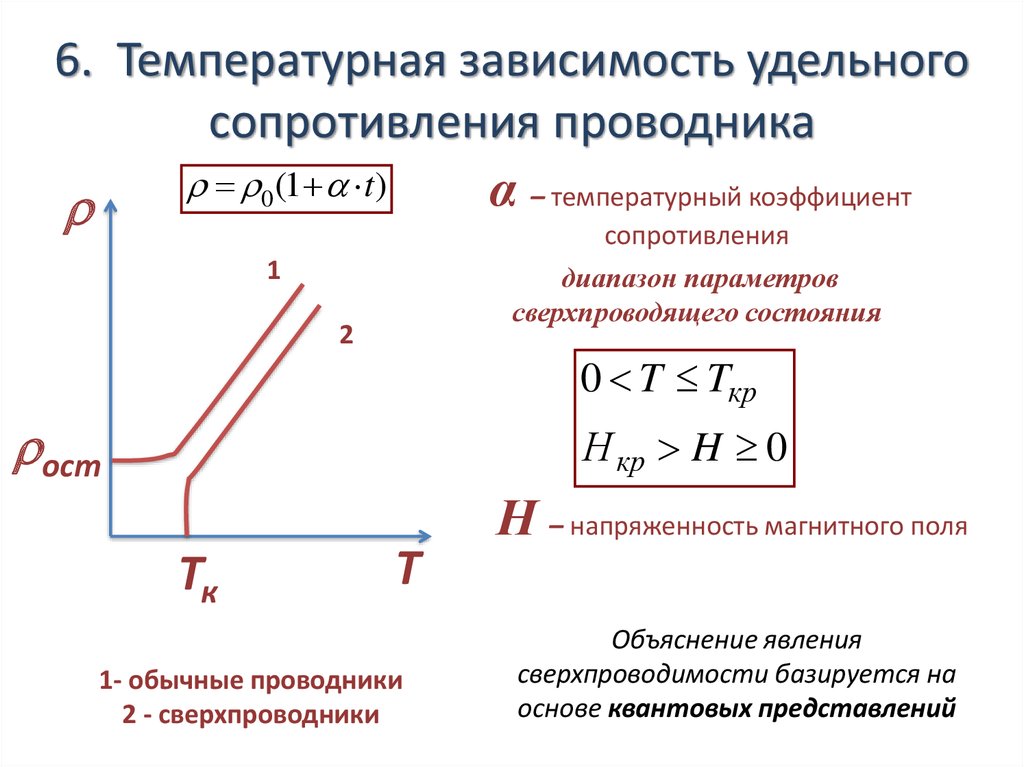
6. Температурная зависимость удельного
сопротивления проводника
0 (1 t)
α – температурный коэффициент
сопротивления
диапазон параметров
сверхпроводящего состояния
1
2
0 T Tкр
ост
Н кр H 0
Тк
Т
1- обычные проводники
2 - сверхпроводники
Н – напряженность магнитного поля
Объяснение явления
сверхпроводимости базируется на
основе квантовых представлений

12.

7. Закон Джоуля-Ленца
A12 qU12
2
U12
IU12 t I R12 t
t
R12
2
- работа постоянного тока
2
A12
U
P
IU12 I 2 R12 12 -мощность, выделяемая
t
R12 в участке цепи
в случае неоднородного проводника
dP
Pуд
на различных dV – разная dP
dV
dl
2
dP jdS
j 2 dV
dS
2
Pуд j
*
Pуд ( j j ) ( j ( E E ))

13.

A12 Q Wхим Амех
- в общем случае
A12 Q
- в частном случае
Тогда, количество теплоты,
выделяемое на данном
участке цепи
Q qU12
2
U12
IU12 t I R12 t
t
R12
2
и
удельная тепловая мощность
Q уд
*
j ( j j ) ( j ( E E ))
2

14.

8. Расчет сложных цепей постоянного тока.

15. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ

Электроны проводимости в металле
ведут себя подобно молекулам газа.
В промежутках между столкновениями
они движутся свободно, проходя путь
между столкновениями (в среднем).
Электроны сталкиваются в основном не
между собой, а с ионами решетки.
8kT
8 1,38 10 23 300
5
Vc
1,1
10
м с.
31
m
3,14 9,1 10
I
enVd
S
Vd
I
Vd
;
enS
10
4
6,2
10
м с.
19
29
6
1,6 10 10 10

16. ЗАКОН ОМА В КЛАССИЧЕСКОЙ ТЕОРИИ

F eE
a
;
m m
Vc
Vdm a ;
Vdm
eE
.
mVc
Vdm
eE
Vd
; j enVd
2
2mVc
ne
j
E;
2mVc
2
j E
1
2mVc
2 .
e n

17. ЗАКОН ДЖОУЛЯ-ЛЕНЦА В КЛАССИЧЕСКОЙ ТЕОРИИ

К концу свободного пробега электрон приобретает дополнительную кинетическую
Энергию
2
2
mVdm
m eE
e2 2 2
Wk
E .
2
2
2 mVc 2mVc
Каждый электрон претерпевает за секунду
столкновений.
1
Vc
Q
1
Vc e 2 2 2 e2 n 2
q
n Wk n
E
E .
2
t V
2mVc
2mVc
E
2
2
Q I R t;
2
2
2
I R E S
l E
l
I jS S ; R q
2
.
lS lS S
S

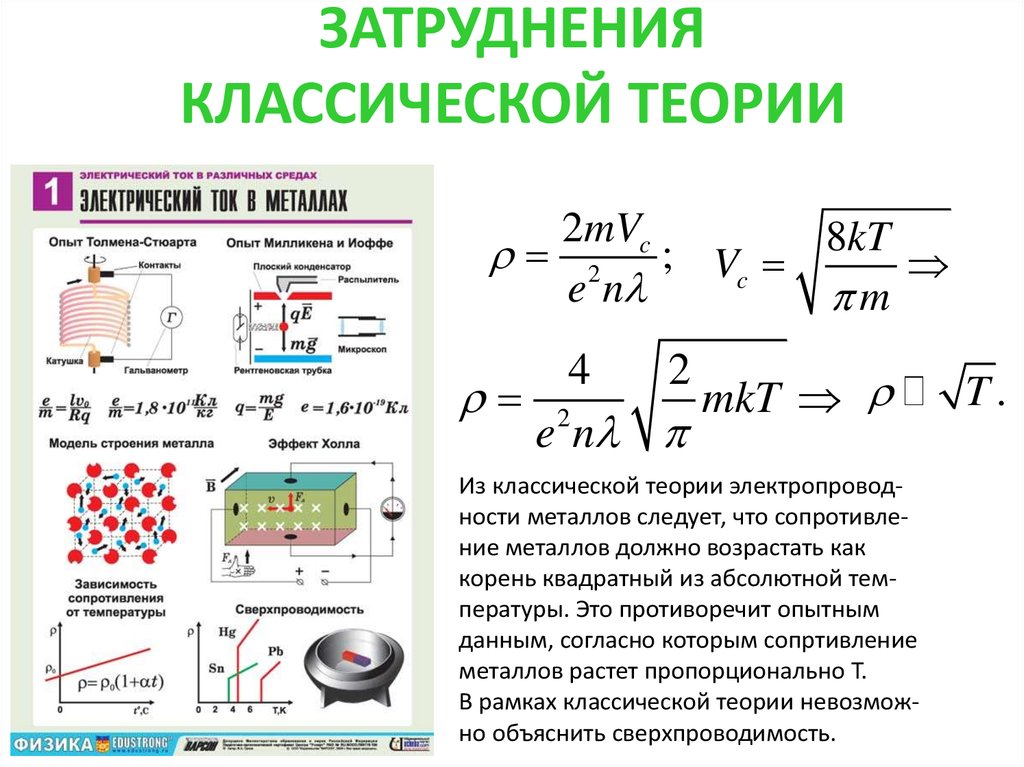
18. ЗАТРУДНЕНИЯ КЛАССИЧЕСКОЙ ТЕОРИИ

2mVc
2 ; Vc 8kT
e n
m
4
2
2
mkT
e n
Из классической теории электропроводности металлов следует, что сопротивление металлов должно возрастать как
корень квадратный из абсолютной температуры. Это противоречит опытным
данным, согласно которым сопртивление
металлов растет пропорционально T.
В рамках классической теории невозможно объяснить сверхпроводимость.
T.