Похожие презентации:
Метод замены множителей
1. Метод замены множителей
Царева В.В.учитель
математики
МОУ
Инзенская
СОШ №2
2. Цели и задачи:
Цель занятия: познакомить учащихся с методомзамены
множителей,
как
эффективным
способом решения целого класса неравенств.
Задачи занятия:
ввести понятие метода замены множителей и
рассмотреть применение этого метода для
решения различных видов неравенств;
повторение и обобщение метода интервалов;
расширение кругозора учащихся;
воспитание познавательной активности;
повышение интереса к изучению математики
на
примере
красоты
метода
замены
множителей;
подготовка учащихся к решению задачи С3
ЕГЭ по математике.
3. i.Повторение. Решение неравенств методом интервалов
а)( х 2)( х 1) 0( х 1)( х 3)
б)
0
х
2
4. II.Метод замены множителей
Определениявозрастающей
и
убывающей
функций можно сформулировать по другому:
Функция
y=f(x)
называется
возрастающей
(убывающей) на множестве M, если для любых а и b из
множества М выражения a-b и f(a)-f(b) имеют одинаковый
(противоположный) знак.
Этот факт можно использовать при решении
неравенств, в правой части которых стоит ноль. Можно в
левой части (числителе и/или знаменателе левой части)
заменить разность значений монотонной функции
разностью значений аргумента. При этом, если функция
возрастающая, то знак неравенства сохранится, а если
функция убывающая, то знак неравенства поменяется на
противоположный. Такой прием решения неравенств и
называется методом замены множителей.
5.
Базовая информация по методу заменымножителей
1.Стандартный вид неравенств, когда
применяется метод замены множителей
u u un
1 2
v v vn 0
1 2
где символ «v» обозначает один из четырех
возможных знаков неравенства: <, >, ,
2.
Основная
идея
метода
замены
множителей состоит в замене любого множителя в
числителе или в знаменателе на знакосовпадающий с
ним и имеющий одни и те же корни.
Замечание. Преобразованное таким образом
неравенство всегда равносильно исходному в области
существования последнего.
Предупреждение. Указанная замена возможна
только тогда, когда неравенство приведено к
стандартному виду.
6. Наиболее часто встречающиеся замены
1) t t 22 (t t )(t t )
2) t1 t 2 t12 t 2
1 2 1 2
3) t1 t 2 t1 t 2
4) t1 t 2 t12 t 2
5) f g f 2 g 2 ( f 0, g 0)
6) log a f log a g ( a 1)( f g )
7) a
f
a
g
( a 1)( f g )
7. III. Закрепление. Решение неравенств
а) х 2 4 хб )( х 1 3)( х 2 5) 0
в) х 6 х 8 0
2
г) х3 1 1 х
д)( х 3)
х 4 х 9
2
2
8. Решение неравенств
а) х 2 4 хРешение :
х 2 4 х 0
( х 2) ( 4 х ) 0
2
2
( х 2 4 х)( х 2 4 х) 0
6( 2 х 2 ) 0
2х 2 0
2х 2
х 1
Ответ : х 1
9.
б )( х 1 3)( х 2 5) 0Решение :
(( х 1) 3 )(( х 2) 5 ) 0
2
2
2
2
( х 1 3)( х 1 3)( х 2 5)( х 2 5) 0
( х 2)( х 4)( х 7)( х 3) 0
х ( 4; 3) (2;7)
Ответ : х ( 4; 3) (2;7)
10.
в) х 6 х 8 02
Решение :
х 6 х 8 0
2
( x 4)( x 2) 0
( x 16)( x 4) 0
2
2
x ( 4; 2) (2;4)
Ответ : x ( 4; 2) (2;4)
11.
г) х3 1 1 xРешение :
x 3 1 (1 x) 0
( x 3 1) 2 (1 x) 2 0
( x 1) 2 ( x 2 x 1) 2 ( x 1) 2 0
( x 1) 2 (( x 2 x 1) 2 1) 0
( x 1) 2 ( x 2 x 1 1)( x 2 x 1 1) 0
( x 1) 2 ( x 2 x)( x 2 x 2) 0
x( x 1) 2 ( x 1)( x 2 x 2) 0
x ( ; 1) (0;1) (1; )
Ответ : x ( ; 1) (0;1) (1; )
12.
г )( х 3) х 2 4 х 2 9Решение :
( х 3) х 2 4 ( х 2 9) 0
( х 3) х 2 4 ( х 3)( х 3) 0
( х 3)( х 2 4 ( х 3)) 0
( х 3)( х 2 4 ( х 3) 2 ) 0
( х 3)( х 2 4 ( х 2 6 х 9)) 0
( х 3)( х 2 4 х 2 6 х 9) 0
( х 3)( 6 х 5) 0
5
х ( ; ] [3; )
6
5
Ответ : х ( ; ] [3; )
6
13. IV. Задания для самостоятельного решения
а)( х 2 4 х2 ) ( х 4 х2 х 2 )
( 1 х 4) ( 3 х х 5 )
Ответ : х ( 3; 2) [2;5)
б )( х 2 х 6) х 2 2 х 3 0
Ответ : х ( ; 3] { 1} [3; )
в)
х 2 7 х 10
0
х 6х 9
Ответ : х ( 5; 2) (2;3) (3;5)
2
0
14. V. литература
1)«Квантор» В. И. Голубев; В. И.Тарасов. «Эффективные пути решения
неравенств».
2)«Сборник по математике доя
поступающих в вузы» под редакцией
М. И. Сканави.
3)Голубев В.И. Решение сложных и
нестандартных задач по математике. –
М.: Илекса, 2007








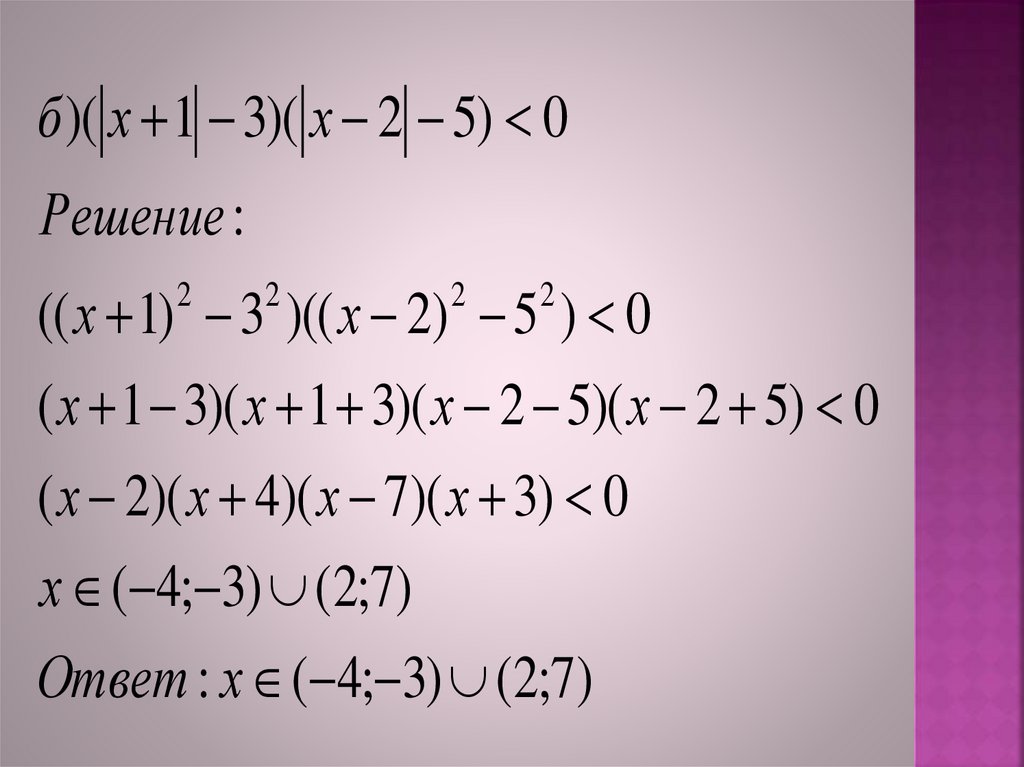


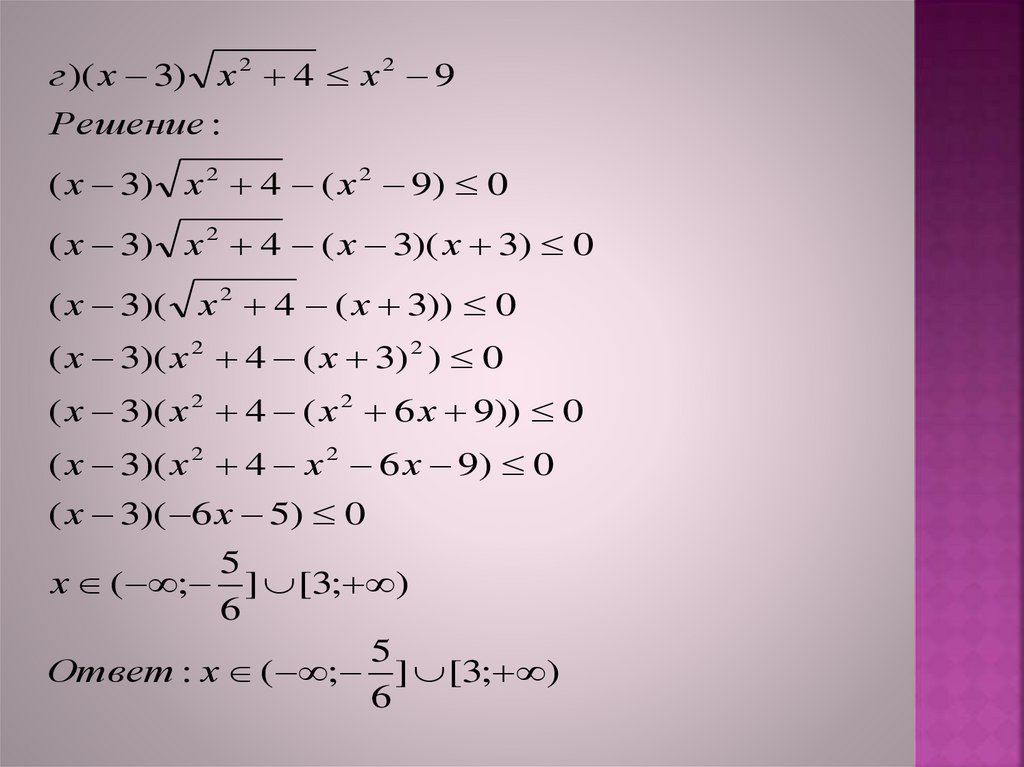



 Математика
Математика








