Похожие презентации:
Метод замены множителей. Показательная и логарифмическая функции и вызываемые ими замены
1.
Основная идея методаЕсли неравенство приведено к стандартному
виду
u u u
1
2
n
v1 v2 vn
0,
(1)
где символ « » обозначает один из четырех
возможных знаков неравенства: , , , , то
любой множитель в числителе или знаменателе
можно заменить на более простой множитель,
совпадающий с ним по знаку и имеющий те же
самые корни.
2.
Замечание.Преобразованное
таким
образом
неравенство равносильно исходному в области его
определения.
Предупреждение. Указанная замена возможна только
тогда, когда неравенство приведено к стандартному
виду.
3.
Монотонность – ключ к заменеУтверждение 1. Функция f (x)
строго возрастает тогда и только тогда,
когда для любых значений t1 и t2 из области определения функции разность
t1 t2 совпадает по знаку с разностью f (t1 ) f (t 2) , то есть
ОДЗ
f t 1 t2
f (t1 ) f (t 2 ) .
Утверждение 2. Функция f (x) строго убывает тогда и только тогда, когда
для любых двух значений t1 и t2 из области определения функции разность
t1 t2 совпадает по знаку с разностью f (t2 ) f (t1) , то есть
ОДЗ
f t1 t2
f (t2 ) f (t1) .
Комментарий. Практически, только замена знакопостоянных множителей не
вытекает из этих утверждений. Поэтому, если нет желания трогать знак
неравенства, всюду положительные множители просто убираем, а всюду
2
ax
bx c с
отрицательные – заменяем на (-1). Квадратный трехчлен
отрицательным дискриминантом заменяем на старший коэффициент (или на
свободный член), то есть ax 2 bx c a c при D 0 .
(2)
4.
Функция y t n и вызываемые ею заменыПоскольку функция y t n при n 0 является строго возрастающей на
множестве неотрицательных чисел (а при нечетном натуральном n – на всей
числовой оси), то в силу утверждения 1 справедливы замены:
t1 t2 t1n t2n при n 0, t1 0, t2 0,
(3)
t1 t2 t12 k 1 t22 k 1 при k натуральном.
(4)
Функции y t 2 и y t , рассматриваемые на множестве неотрицательных
чисел, являются строго возрастающими, то есть
t1 t2 t12 t22 t1 t2 .
Поэтому
t1 t2 t12 t22 ,
t1 t2 t1 t2 , где t1 , t2 0.
(5)
(6)
2
m
m
Так как m 0 и
для любого m, то получаем, что
2
t1 t 2 t1 t 2 t12 t 22 .
2
2
(7)
5.
Пример 1. Решить неравенствоx 2 4 x x 4
2
x2 x 2
1 x 4 3 x x 5
0.
(8)
Решение (подробное). Исходное уравнение имеет вид
u1 u2
0.
v1 v2
Все множители u1, u2, v1 и v2 имеют вид t1 t2 , где t1 0 и t2 0 поэтому, в
силу (5), эти множители можно заменить на знакосовпадающие с ними
множители вида t12 t22 :
(8)
x 2 2 4 x 2 2 x 4 2
1 x
2
x
2
42 3 x x 5
2
x 2
0.
2
2
2
2
2
Так как m m и x x 2 x x 2 , то с учетом неотрицательности
подкоренного выражения получаем:
2
6.
22
2
2 2
2
x
2
4
x
x
4
x
x
2
0,
2
2
2
(8)
1 x 42 3 x x 5
x 2 x 2 0
x 2 4 x 2 x 2 4 x 2 9 x 18
0,
1 x 4 1 x 4 3 x x 5 3 x x 5
x 1 или x 2
9 x 2 x 6 x 2 x 2 x 2
0,
16 x 3 5 x x 1
x 1 или x 2
2
2
где знакопостоянные (D<0) квадратные трехчлены x x 6 и x x 2
согласно (2) заменяем на (-1) и 1 соответственно
7.
1 1 x 20,
x 3 x 5 x 1
x 1 или x 2
3 x 2 или 1 x 5,
x 1 или x 2
Ответ: 3 x 2; 2 x 5.
x 2
0,
x 3 x 5 x 1
x 1 или x 2
3 x 2,
2 x 5.
8.
Две любопытные замены:t
t ,
(9)
f g
f g.
(10)
ОДЗ
ОДЗ
Замена (9) очень удобна там, где приходится отслеживать
область допустимых значений.
Замена (10) суммы f g при возможном одновременном
равенстве нулю подкоренных выражений на сумму f g
позволяет учитывать эту возможность.
9.
Пример 2. Решить неравенствоx
2
x 6 x 2 2 x 3 0.
Решение.
x x 6 x 2x 3 0
x x 6 x 2 x 3 0,
2
2
2
2
2
x 2 x 3 0
x 3,
x 1,
x 3 x 2 x 1 x 3 0,
x 1 или x 3
x 3.
Ответ:
; 3 1 3; .
10.
Пример 3. Решить неравенствоx 10 3x x 14 2 x 0.
Решение. Множители
уже нельзя
x 10 3 x и x 14 2 x
рассматривать как разности неотрицательных величин, так как выражения 3x
и 2x в области допустимых значений (то есть при x 10 0 ) могут
принимать как положительные, так и отрицательные значения. Однако, если
ОДЗ исходного неравенства разбить на два промежутка 10 x 0 и
x 0 (при x=0 выражения 3x и 2x меняют знак), то легко заметить, что на
промежутке 10 x 0 мы имеем произведение двух положительных
чисел, и поэтому исходное неравенство ложно, а на втором промежутке
каждый множитель есть разность двух неотрицательных чисел, а
следовательно, можно воспользоваться методом замены множителей. Итак,
10 x 0,
x 10 3 x x 14 2 x 0 ( ложно)
x
0
,
x 10 3x x 14 2 x 0
2
2
2
2
x
10
3
x
x
14
2
x
0
11.
x 0,2
2
2
x 10 9 x x 14 2 x 0
x 0,
2
9 x x 10 x 14 2 x x 14 2 x 0
x 0,
10
9 x 1 x 9 14 x 3x 14 0
x 0,
10
x 9 x 14 0
так как при x>0 (x+1) и (3x+14) – положительные числа
x 0,
10
x 14.
10
9
x
14
9
10
;
14
.
Ответ.
9
12.
Показательная и логарифмическая функциии вызываемые ими замены
Показательная функция y a строго убывает при 0 a 1
и строго возрастает при a 1 . Поэтому, в частности, для a 10
получаем
t
t
t
10 1 10 2 t1 t2 .
Для произвольного основания a, пользуясь
логарифмическим тождеством, можно увидеть, что
a a 10
t1
Откуда
t2
10
lg a t1
lg a t 2
10
t1 lg a
основным
10
t 2 lg a
.
a a t1 lg a t2 lg a,
t1
t2
то есть a a t1 t2 lg a.
t1
t2
(11)
13.
Функция y lg x - строго возрастающая. Поэтомуx1 x2
lg x1 lg x2 .
ОДЗ
Если x1=a и x2=1, то получаем, что
a 1 lg a lg 1,
то есть lg a a 1.
(12)
Откуда соотношение (11) принимает вид
a t1 a t2 t1 t2 a 1 .
(13)
Таким образом, разность степеней с одним и тем же основанием
по знаку совпадает с произведением разности показателей этих
степеней на разность основания и единицы.
14.
Для логарифмической функцииустанавливаем
y log a t
аналогично
lg t1 lg t2
1
lg t1 lg t2 .
log a t1 log a t2
lg a lg a lg a
Отсюда следует, что
lg t1 lg t2
t1 t2
log a t1 log a t2
.
lg a
a 1
То есть разность логарифмов по одному и тому же основанию
всегда по знаку совпадает с отношением разности
подлогарифмических выражений к разности основания и
единицы:
t1 t 2
log a t1 log a t 2
.
a 1
(14)
15.
Замечание. Утверждения (14) и (13) равносильны, посколькупоказательная и логарифмическая функции взаимно обратны.
Эти утверждения также позволяют эффективно решать многие
неравенства, которые принято относить к разряду задач
повышенной сложности. В частности, из (13) и (14) получаются
полезные
схемы
решения
основных
показательных
логарифмических неравенств:
1)
f g a 1 0,
a a
a 0;
2)
a f b,
f log a b a 1 0;
b 0
f
g
16.
3)f g a 1 0,
f 0,
log a f log a g
g 0,
a 0;
4)
f a a 1 0,
log a f b f 0,
a 0;
b
17.
fg 1 a 1 0,f 0,
5) log
a f log a g 0
g
0
,
a 0;
a a
f1 g1
0
0.
g1
g2
a a
f2 g2
f1
6)
f2
18.
Практика19.
Пример 1.x 2 7 x 10
x 6x 9
2
0.
Решение.
x 7 x 10
x 6x 9
2
x 7 x 10
2
2
0
x 3
x 2 x 5
x
0
2
2
0
2 2 x 2 52
0
2
x 3
x 3
x 2 x 2 x 5 x 5
0
2
x 3
x 5; 2 2; 3 3; 5 .
2
20.
Пример 2. 4 x 2 2 x 1x2 x
1.
Решение.
4 x
2
2x 1
x2 x
1
x2 x 4x2 2x 1 1 0
x 2 x 1 2 x 1 0
x ; 0,5 1; .
21.
Пример 3.x
2
x 1
x 5
x 2
3
x x 1 .
2
Решение.
x
2
x 1
x 5
x 2
3
x x 1
2
x 5 2
3 x x 1 1 0
x 2
2 x 1 x x 1
0
x 2
x 2; 1 0,5; 0 .
22.
Пример 4. 24 x 2 1
5 3.
Решение.
2
4 x 2 1
2
5 3 2
4 x 2 1
2 2
3
4 x 2 1
4 x 2 1
5 3 2
2 0
1
4 x 2 1
5 3 0
4x2 1 3 4x2 1 1 0
1
1
x 1 x 1 x
x
0
2
2
1 1
x 1;
; 1 .
2 2
23.
Пример 5. 1 3x 2 x
9.
Решение.
1 3
x2 x
9 0 x2 x 2
x x x x 2 0
2
2
2
2
2
x x x x 2 x x 2 0
2
2
x x 1 x 1 x 2 0
2
2
x 1; 0 0; 1 1; 2 .
24.
3Пример 6.
2 x 1
4
Решение.
3
2 x 1
3
4
3
x 1
3
3
2 x 1
1 3
x 1
3
x 1
.
4 3
3
x 1 2
x 1
3 0
3 0 x 1 0 x 1 1 0
x 1
2
x 1 1 x 1 1 0
x 1 x 2 x 0
2
x 0; 1 1; 2 .
25.
Пример 7. log 2 3 2 x 1.x
3 2 x x 2
0,
2
x
1
log x 2 3 2 x 1 3 2 x 0,
x2 0
x 1 x 3
0
,
x 1 x 1
3
x ,
3 x 1.
2
x 0
Решение.
26.
log35
x
a
Пример 8.
3.
log a 5 x
3
Решение.
log 5 x 35 x 2 0,
3
log a 35 x
3 a 0,
log a 5 x
a 1
35 x 3 5 x 3 5 x 1 0,
3
35 x 0,
5 x 0,
a 0, a 1
27.
15 x 2 75 x 90 4 x 0,3
x 35,
x 5,
a 0, a 1
x 2 x 3 x 4 0,
3
x 35 ,
x 5,
a 0, a 1
2 x 3.
28.
Пример 9. log x x 1 log 1 2 x .Решение.
x
1
log x x 1 log 1 2 x log x x 1 log x
2 x
x
1
2 x x 1 x 1 0,
2 x 0,
x 1 0,
x 0
29.
x 2 x 1 x 10,
x 2
0 x 2
1 5 1 5
1
x 1
x
2
2
0,
x 2
0 x 2
1 5 1 5
0 x 1
1
x 1 0,
x
2
2
или
1 5
0 x 2
x 2.
2
30.
Пример 10. 5logx
8 12 x
x 6
25.
Решение.
logx
5
8 12 x
x 6
8 12 x
25 log x
2
x 6
8 12 x
2
x 6 x x 1 0,
8 12 x
0,
x 6
x 0
31.
8 12 x x 3 6 x 2 x 10,
x 6
2 3x
0,
x 6
x 0
x 2 3 x 1
0,
x 6
2 x 6
3
2
x 1 или 2 x 6.
3
32.
Пример 11. log x log 2 4 x 12 1.Решение.
log x log 2 4 x 12 1
log 2 (4 x 12) x x 1 0,
log 2 (4 x 12) 0,
x 0,
x 1
33.
4 x 12 2 x x 1 0,x
22 x 2 x 12 x 1 0,
4 12 1 0,
x 0,
x log 4 13
x 1
2 x 3 2 x 4 x 1 0, 2 x 22 x 1 0,
x log 4 13
x log 4 13
x 2 x 1 0,
log 4 13 x 2.
x log 4 13
34.
Пример 12. log 3 4 x 1 log x 3 2,5.4 1
Решение.
log 3 4 x 1 log 4x 1 3 2,5
1
5
log 3 4 1
x
log 3 4 1 2
x
2
2 log 3 4 1 5 log 3 4 x 1 2
0
x
log 3 4 1
x
2 log 3
4
x
1 2 log 4
log 4 1
3
x
3
x
1
1
2
0
35.
4x
1 9 4 1 3
0
x
4 1 1
x
4
x log 4 8 x log 4
x
8 4x
4x
3 1 0
3
x x log 4
2
x log 4
0
3 1
3
3 1 или x .
2
3 1 0
36.
Пример 13. log 3 3 x 1 log 1 3 x 2 9 3.3
Решение.
log 3 3 1 log 1 3
x
x 2
3
9 3
log 3 3x 1 log 3 9 3x 1 3 0
log 3 3x 1 2 log 3 3x 1 3 0
log 3 3 1
x
2
2 log 3 3x 1 3 0
log 3 3x 1 3 log 3 3x 1 1 0
37.
1 xx
3 1 3 1 3 0
27
x 28 x
3 3 4 0
27
28
x log 3 x log 3 4 0
27
28
log 3
x log 3 4.
27
38.
Пример 14.Решение.
2
x
3 2
x
2
x
3 2
x 2 log2 x log2 x 6
1.
x
log2
x 6
1
x
2 3
2 log2 x log2 x 6
1,
x
1
2
x 0
2
x
x 6 0,
x x 6 2 2 3 0,
x 0
x 0
2
2x
x
x 3 x 2 0,
x 3.
x 0
39.
Пример 15. log 1 x 3 log 1 x 3 log x 3 2 0.Решение.
2
2
x 3
log 1 x 3 log 1 x 3 log x 3 2 0
2
2
x 3
1
log 2 x 3 log 2 x 3
0
x 3
log 2
x 3
x 3
x 3
log 2 x 3 1 log 2 x 3 1
0,
x 3
log
2
x 3
x 3 0
40.
x 3 x 3 1x 3 2 x 3 2
0,
x 3
1
x 3
x 3 0
9 x x 9
9 x x 9 0,
0,
x 3
x 3 0
x 3 0
3 x 9.
41.
Пример 16.1 log 2 p x
log p
0.
1 log p x
Решение.
1 log 2 p x
1 p 1 0,
2
1
log
x
1 log p x
p
log p
0
2
1 log p x
1 log p x
1 log x 0
p
log 2 p x log p x p 1
0,
1 log p x
1 log x 0
p
42.
log p x log p x 1 p 1 0,1 log p x 0
1
x 1 x p 1 0,
p
x p p 1 0
0 p 1,
p 1,
1
1
x 1 x 0, или x 1 x 0,
p
p
x p 0
x p 0
43.
0 p 1,1
p
x
1
или
x
p
При p 1 решений нет.
или
p 1,
1
x
1
.
p
44.
x log 5 x 2 log 3 xПример 17. log 5 x log x
.
3
log 3 x
Решение.
x log 5 x 2 log 3 x
log 5 x log x
3
log 3 x
2 log 5 x log 5 x log 3 x
1
log 5 x 1
0
log 3 x
log 3 x
2 log 5 x log 3 x log 3 x 1 2 log 5 x
0
log 3 x
45.
2 log 5 x log 3 x 1 log 3 x 10
log 3 x
1
log 3 x 1 log 5 x
2
0
log 3 x
1
x 3 x
1
5
или 1 x 3.
0, 0 x
x 1
5
x 0
46.
Пример 18. log x 4 2 x 9 x 4 1.Решение.
2
log x 4 2 x 9 x 4 1
2 x 2 9 x 4 x 4 x 4 1 0,
2
2 x 9 x 4 0,
x 4 0
2
2
2 x 9 x 4 x 4 2 x 4 2 1 0,
2
2 x 9 x 4 0,
x 4
2
47.
2 x 2 9 x 4 x 4 2 x 2 9 x 4 x 4 x 4 1 x 4 1 0,1
x или x 4
2
2 x 2 10 8 2 x 2 8 x x 5 x 3 0,
1
x или x 4
2
x 1 x 4 2 x x 5 x 3 0,
1
x или x 4
2
x 0
или
x 5.
48.
xПример 19. log 3 x log 3 .
9
Решение.
x
log 3 x log 3 log 2 3 x log 2 3 x
9
9
x
x
log 3 x log 3 log 3 x log 3 0
9
9
log 3 x log 3 x 2 2 log 3 x 2 0
x 3 0,
log 3 x 1 0
0 x 3.
x 0
49.
Пример 20. 8 3x 4 x
9
x 1
4
9 x.
Решение.
8 3
x 4 x
9
4
x 1
9
9 3 3
x
3
4
x
9 3
4
x
x
4
3
x
9 3
4
x
x
0
4
x
x
3 3 3
2
3 3
4
x
3
x
3
4
x
x
3
x
9 3
4
x
2
0
x
3
x
0
50.
2 4 x3
3
x
0
2 4 x x 0
x 4 x 2 0
4 x 2 0
4
4
x 2
4
x 1 0
x 2
0 x 16.
51.
Итоги52.
Основные замены:t1 t2 f (t1 ) f (t 2),
если f(t) – строго возрастающая функция;
t1 t2 f (t2 ) f (t1),
если f(t) – строго убывающая функция.
53.
Наиболее часто встречающиеся замены(без учета ОДЗ):
t t ;
2
t1 t2 t1 t2 ;
2
2
at bt c a при D 0;
2
54.
t1 t2 t1 t2 ;t1 t2 t1 t2 ;
2
t at bt c t at bt c ,
2
2
2
при D 0;
55.
a a t1 t2 a 1 ;t1
t2
a 1 t a 1 ;
t1
f g f g при f 0 и g 0;
2
2
56.
log a f f 1 a 1 ;log a f g f a
g
a 1 ;
log a f log a g f g a 1 .
57.
Литература:Голубев В. И. Метод замены множителей, М:
Архимед. Лекции и задачи. Вып. 4., 2006 г.
Голубев В. И., Шарыгин И.Ф. Эффективный
путь решения неравенств М. Квантор 1993 г.










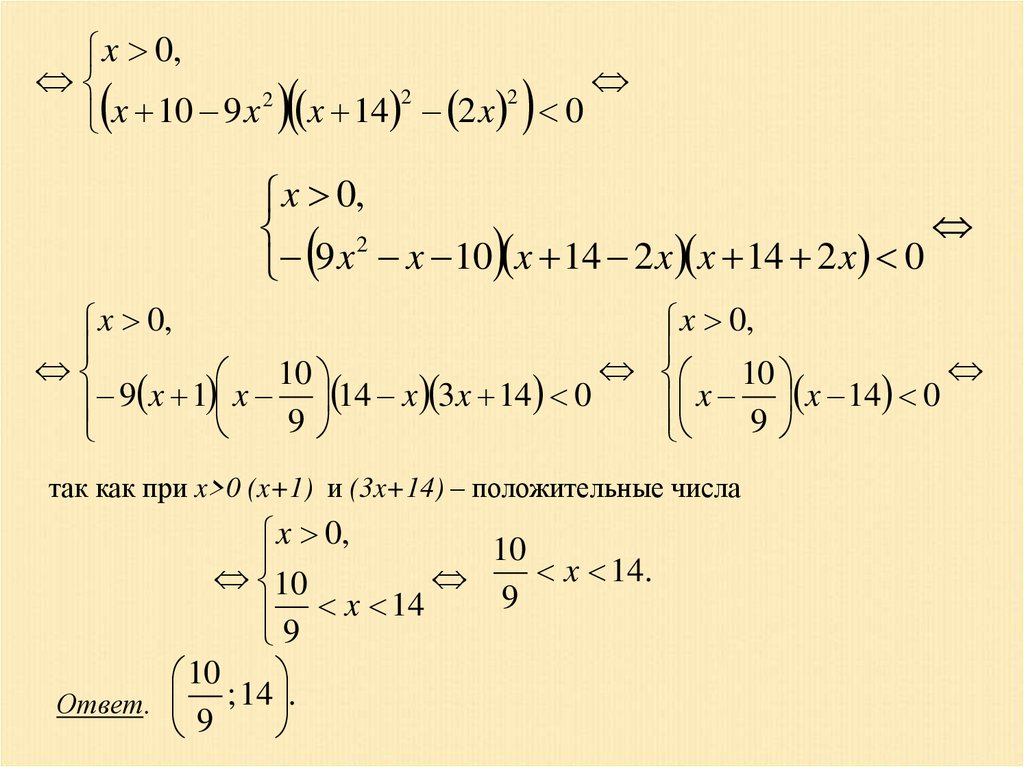




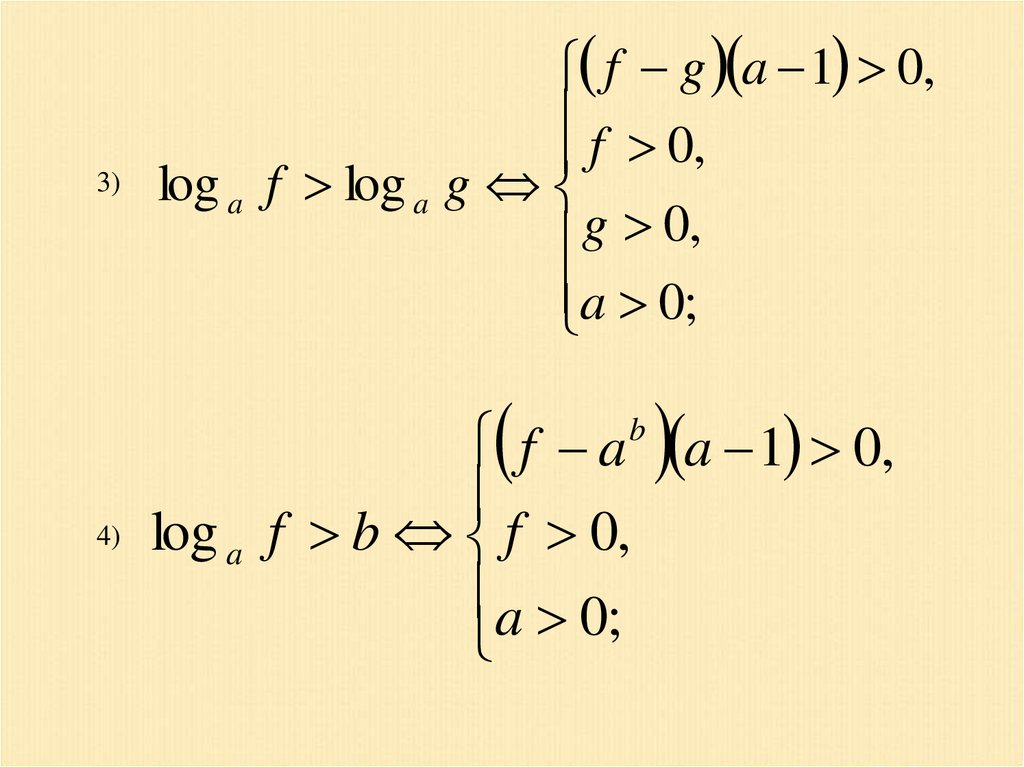
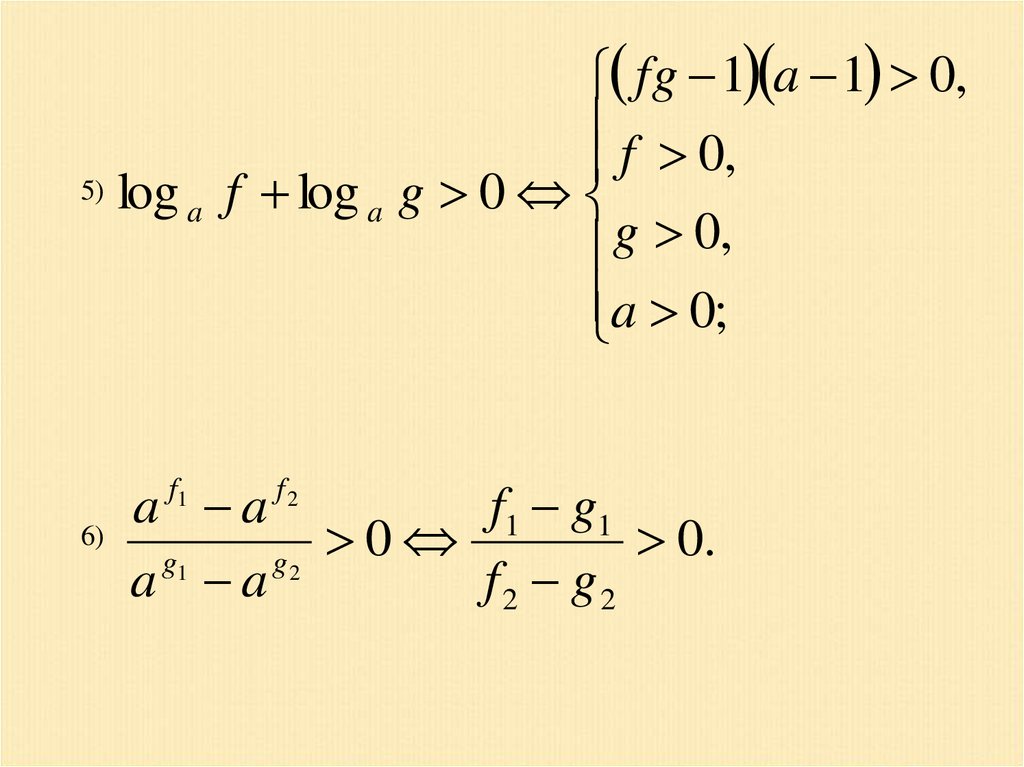

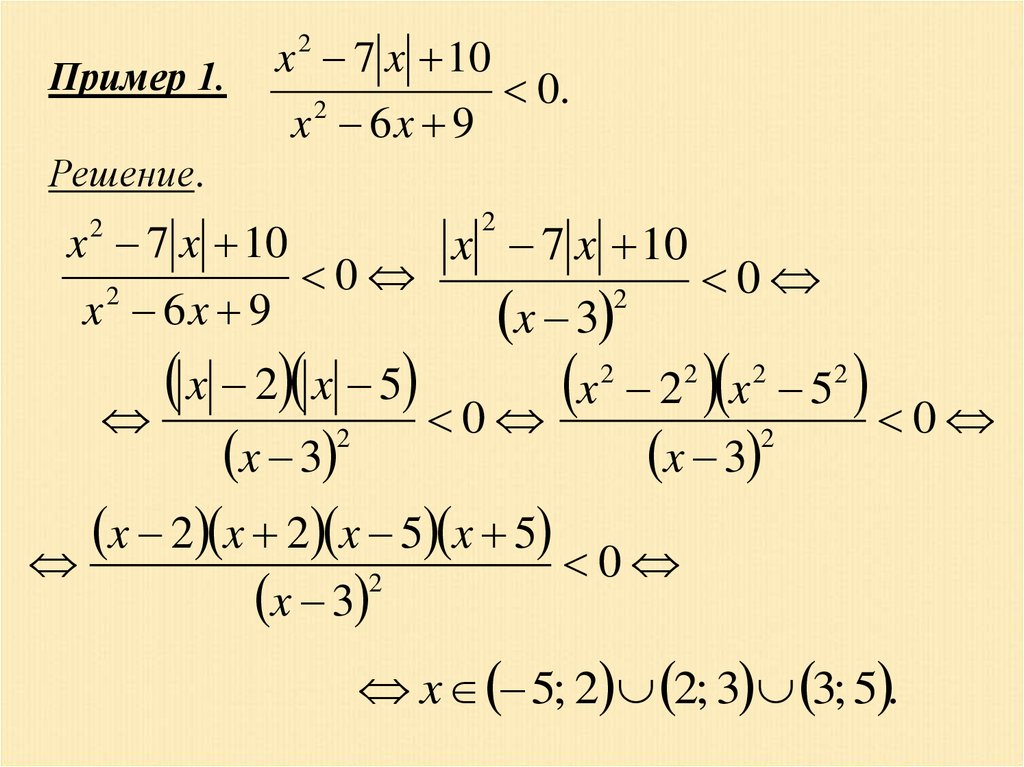

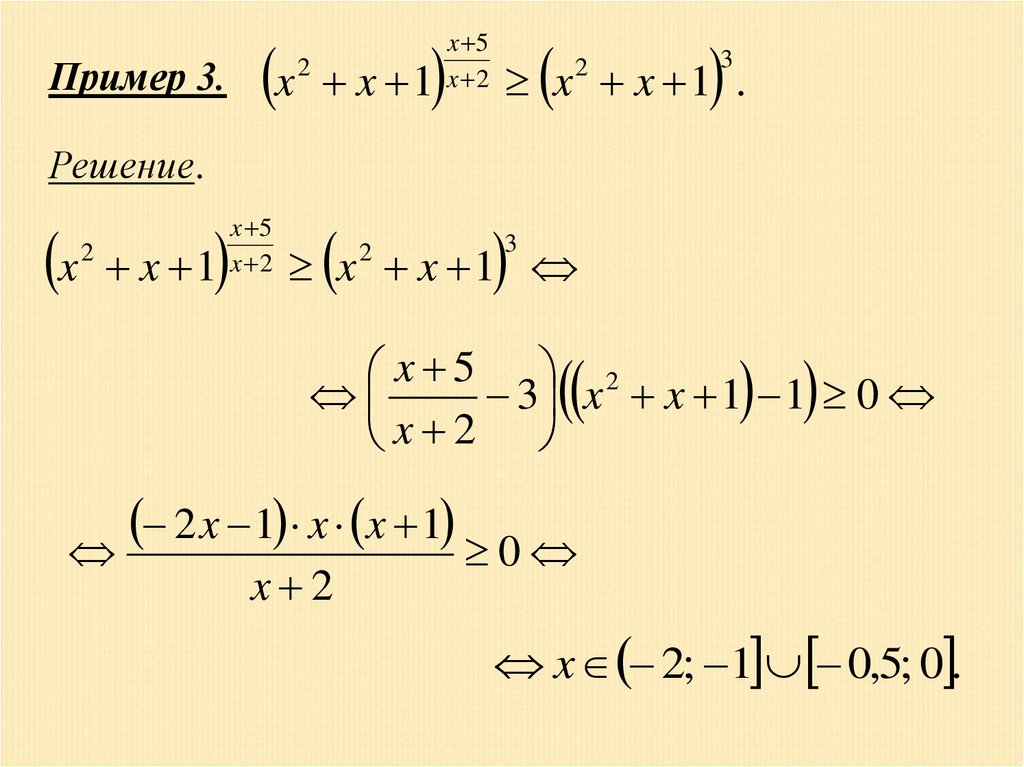

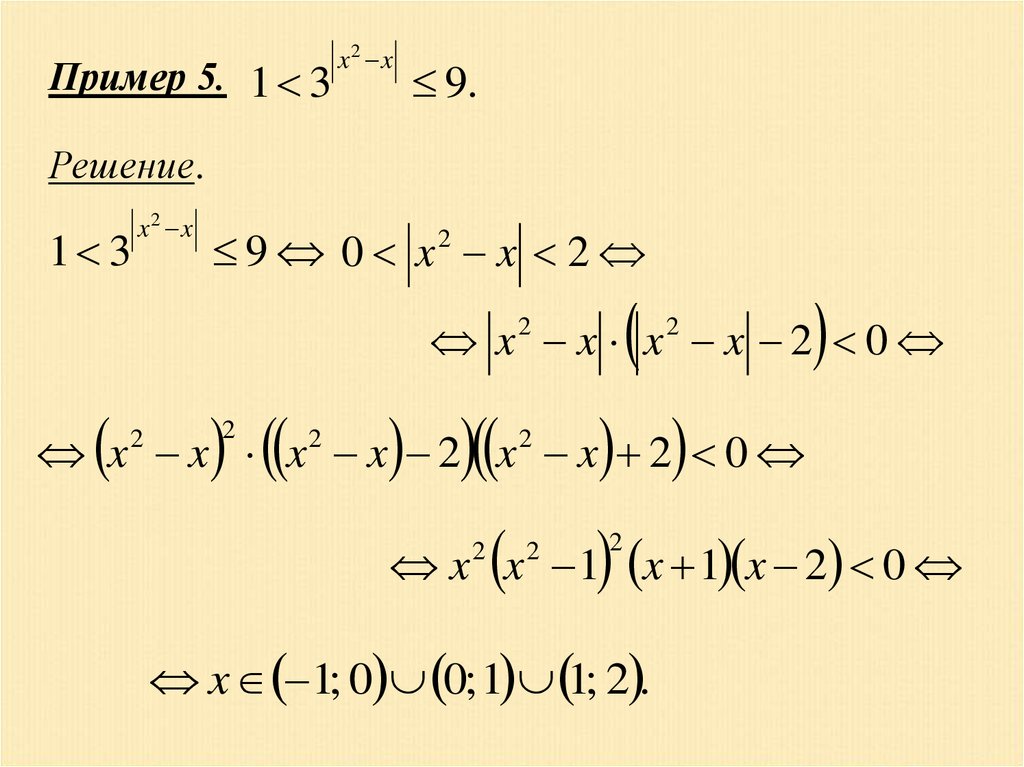
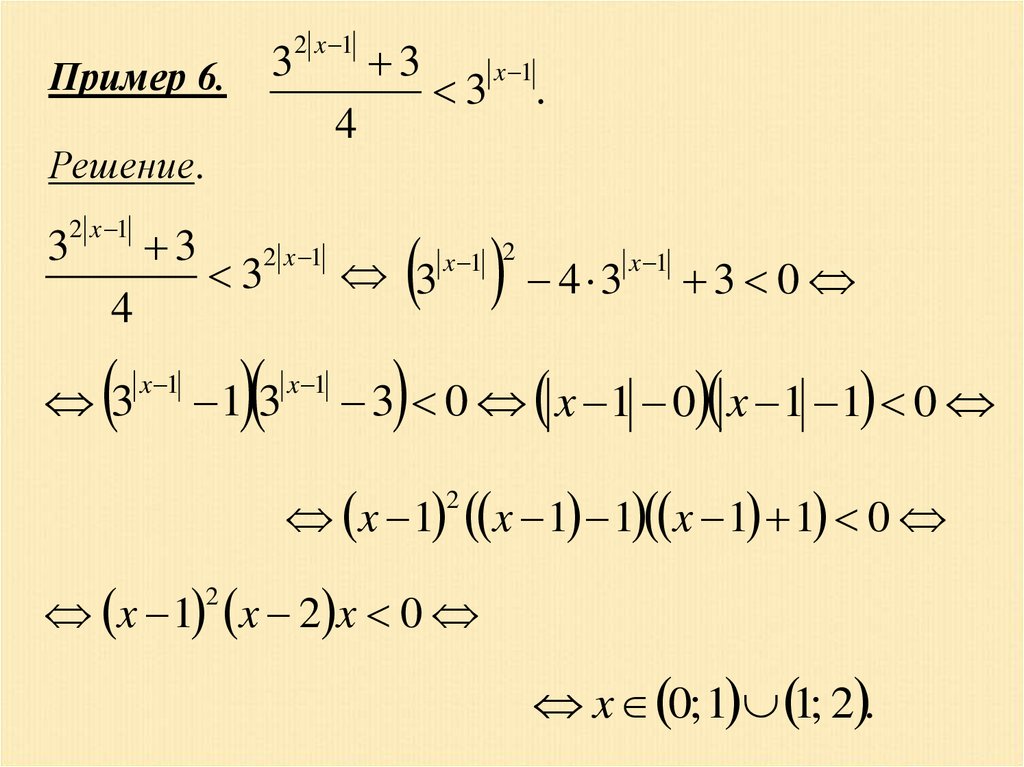

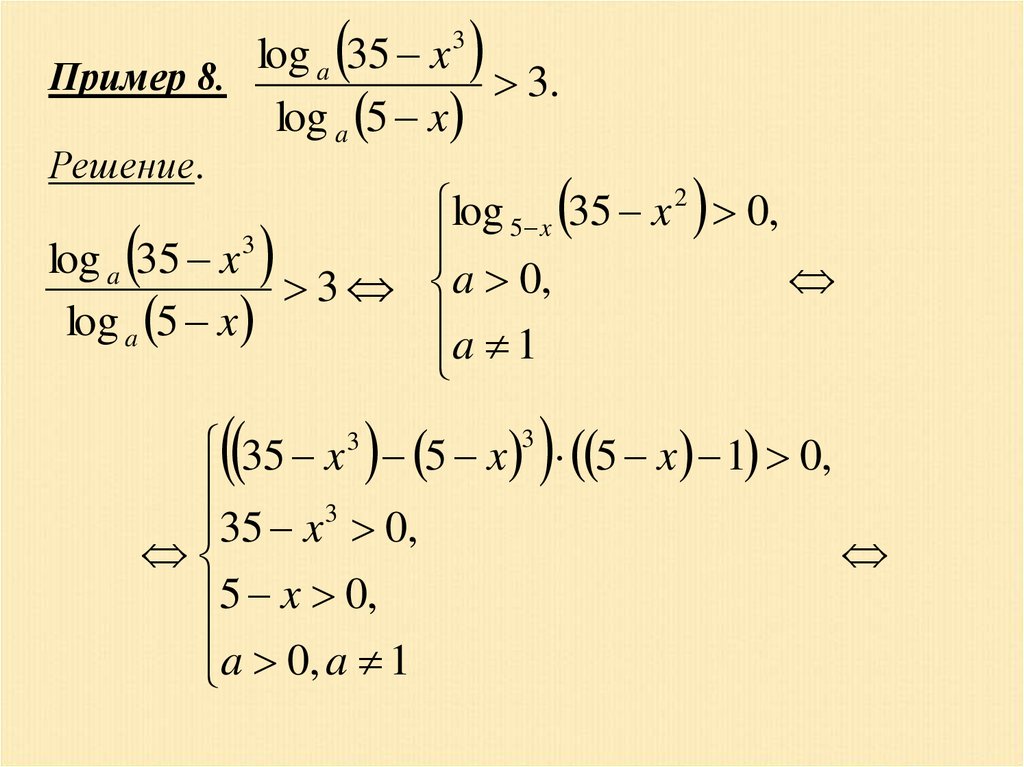

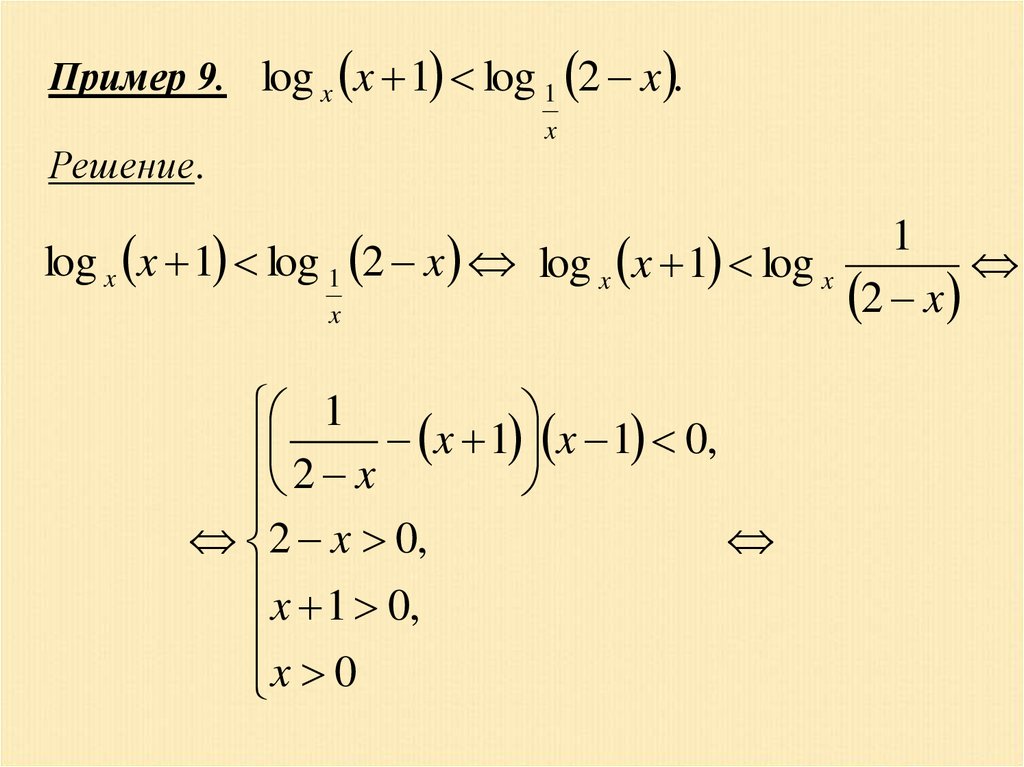




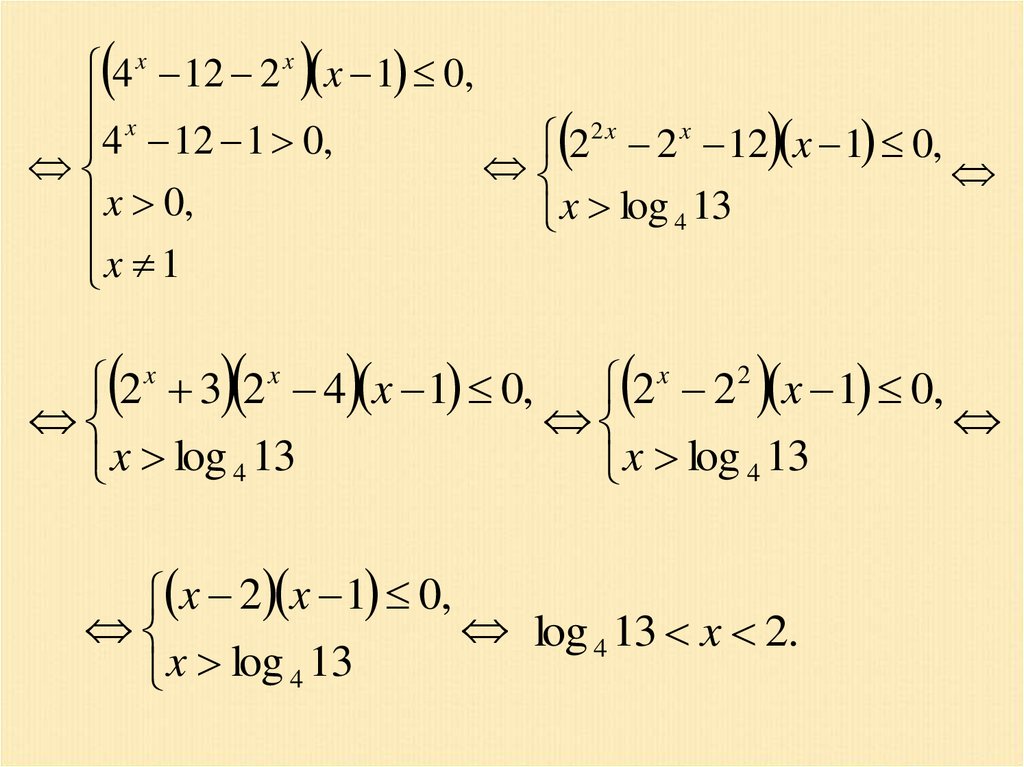


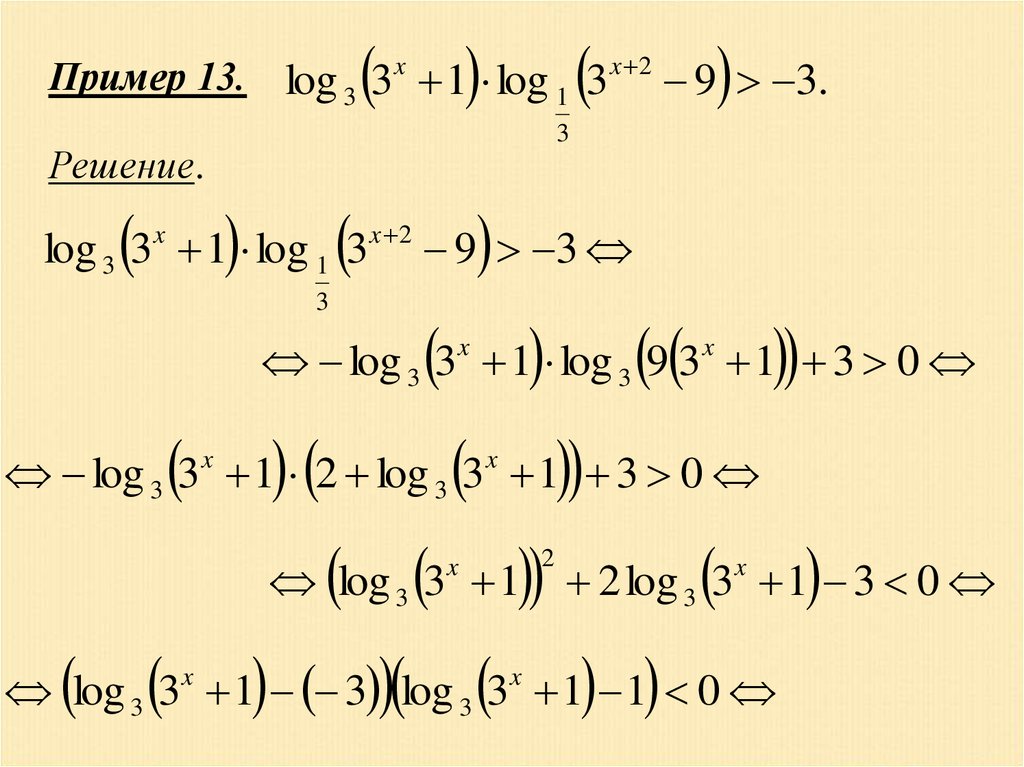
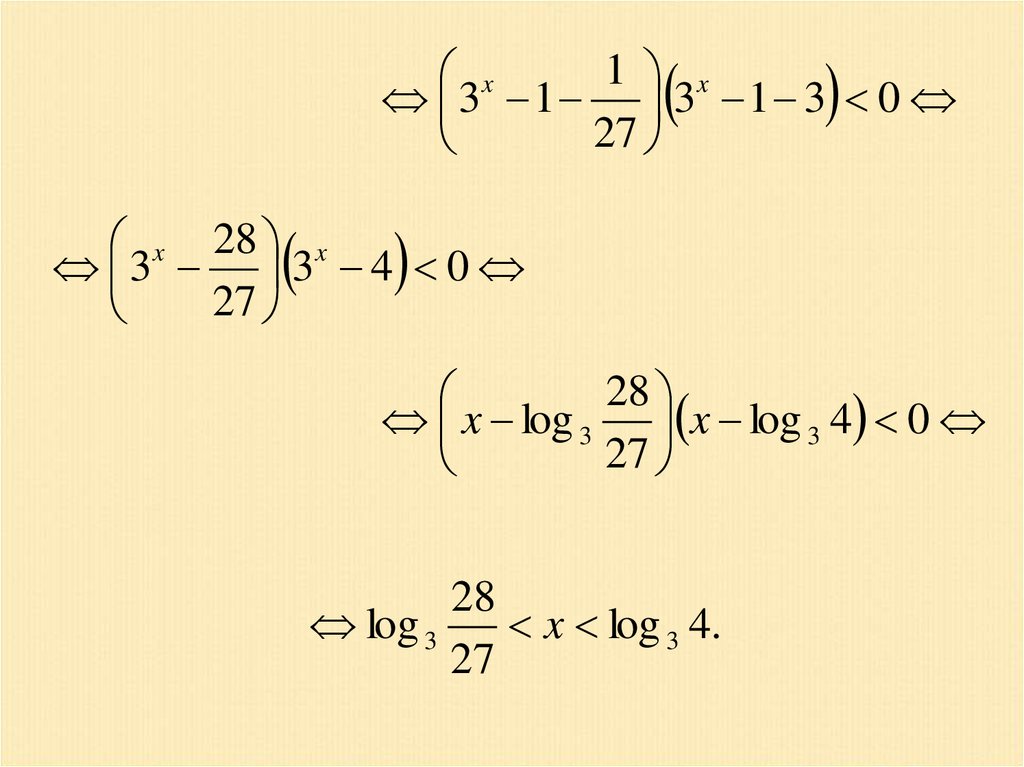


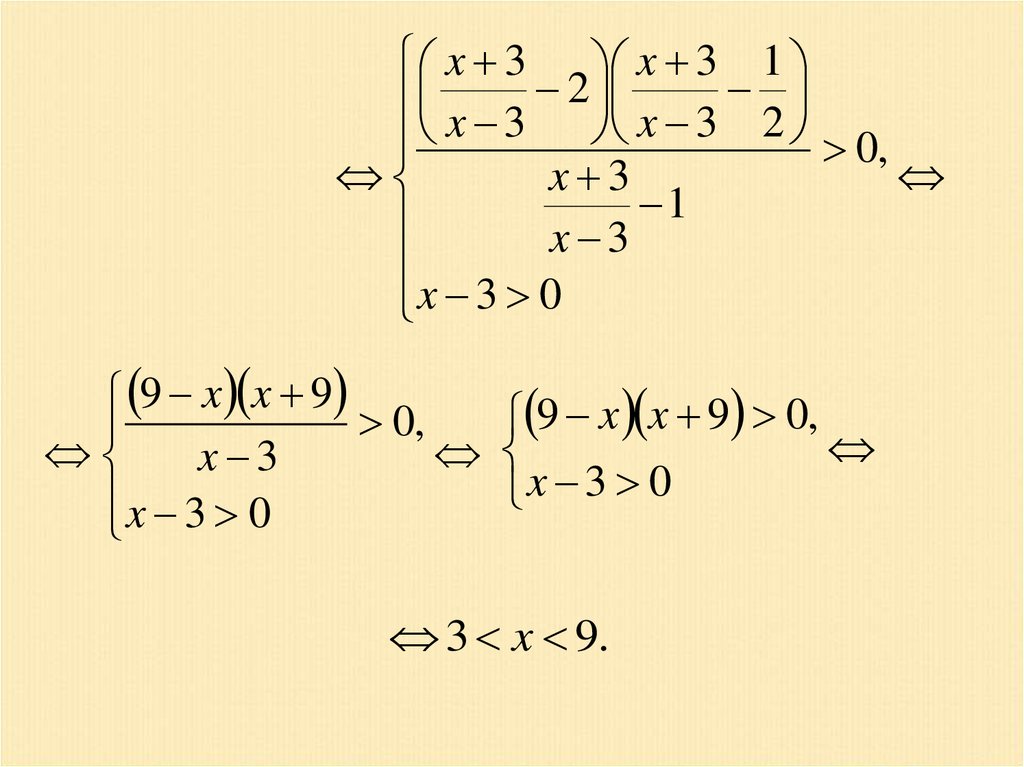

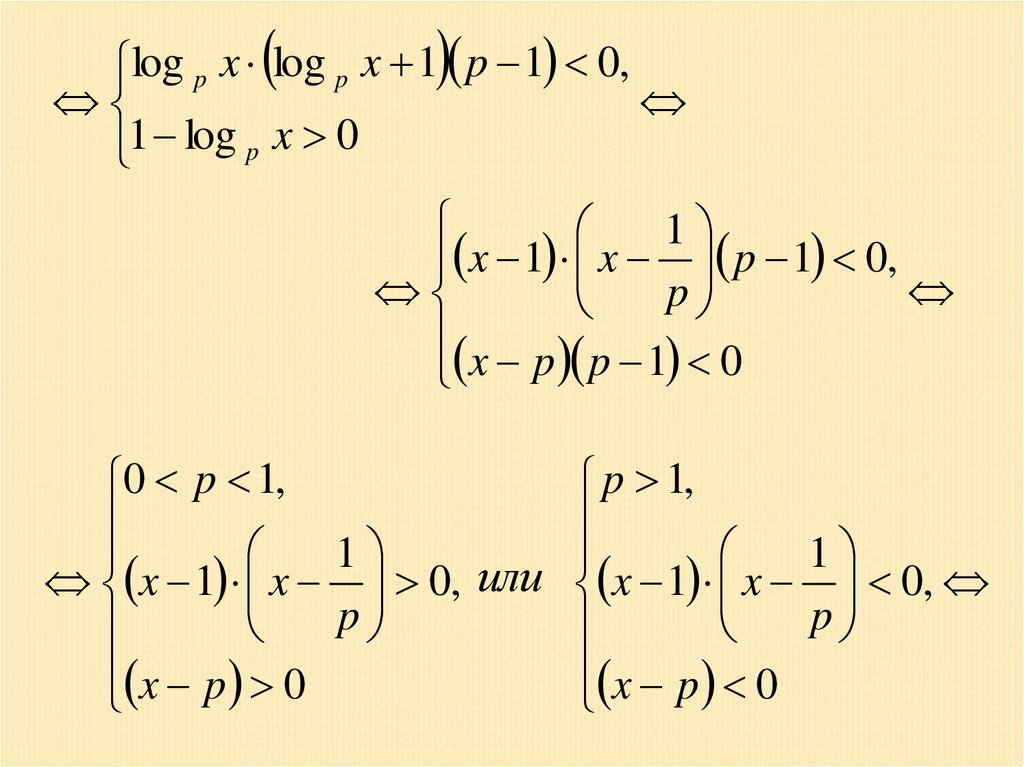


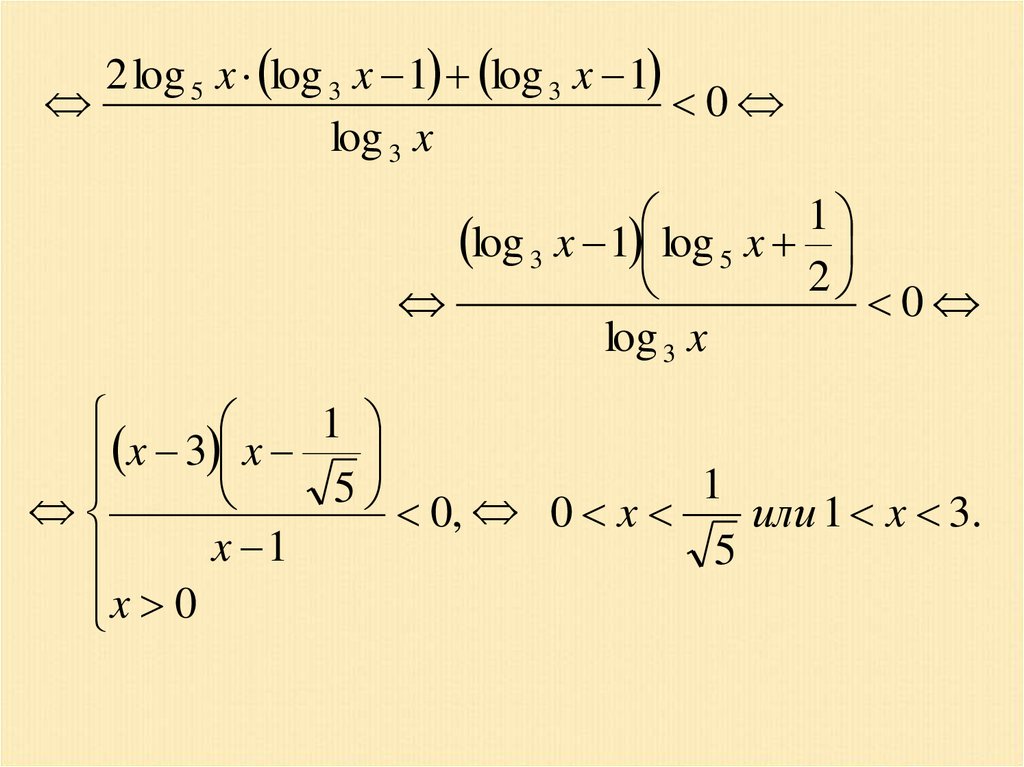

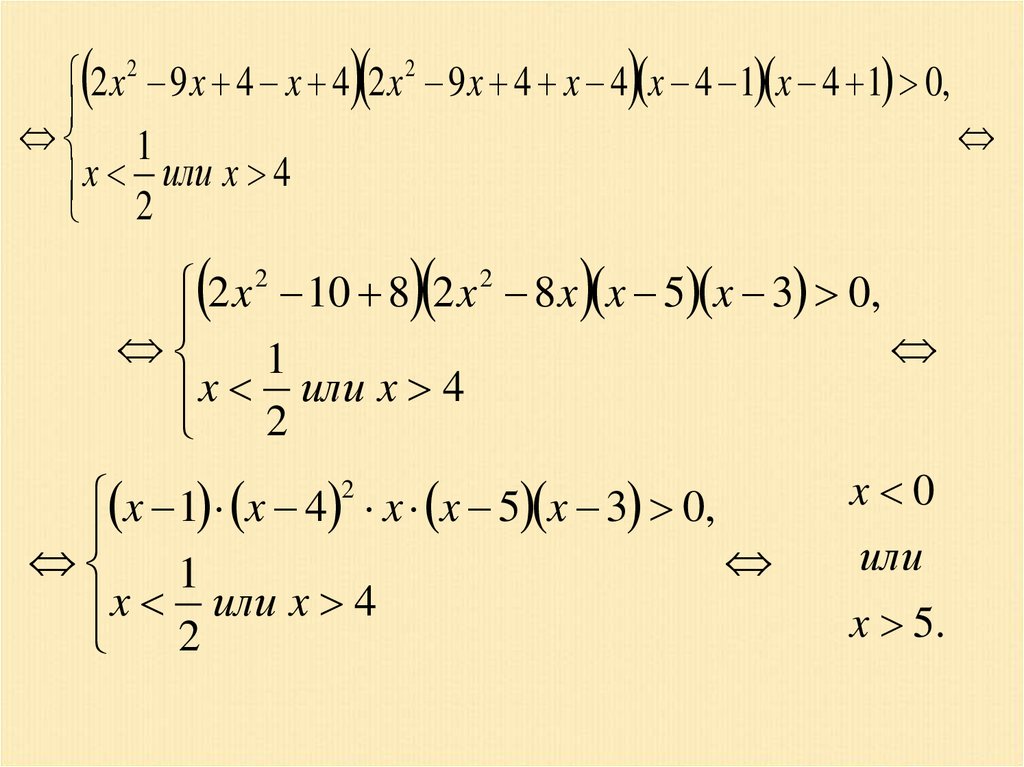






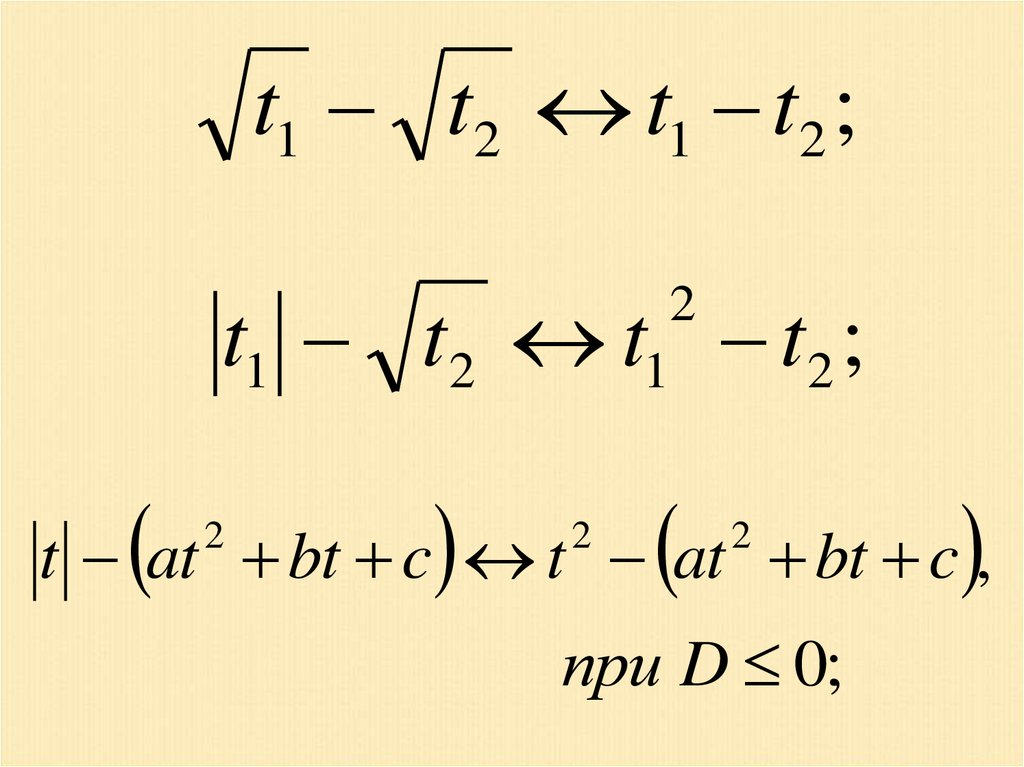
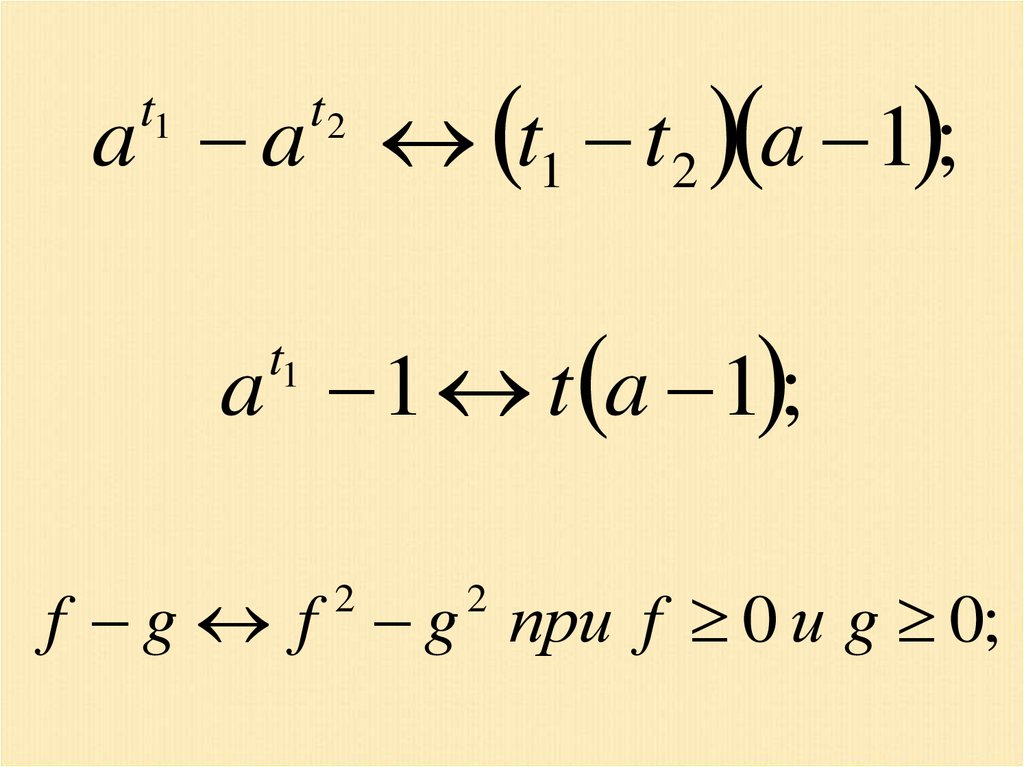
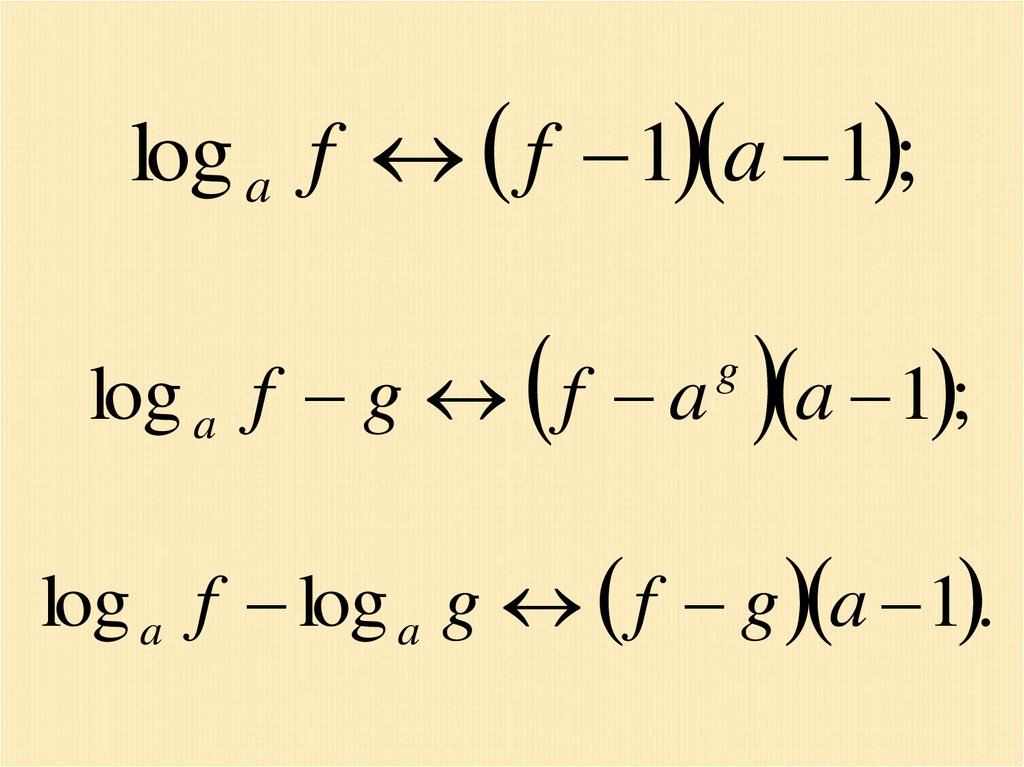

 Математика
Математика








