Обратные тригонометрические функции. Свойства и графики

1.

Обратные
тригонометрические
функции.
Свойства и графики.
ГБОУ ЦО № 173
Попова Лариса Анатольевна

2.

Обратные тригонометрические
функцииОпреелене arcsin
arcsin ( 1
П П
;
(число) из
2 2
Арксинусом числа
промежутка
arcsin
Примеры:
называется угол
синус которого равен
П П
;
2 2
sin
1 П
П
arcsin , arcsin( 1)
2 6
2
arcsin
3
П
П
, arcsin( 1 )
2
3
2
Функция y = arcsinx - нечетная, т.к. arcsin(-x) = - arcsinx

3.

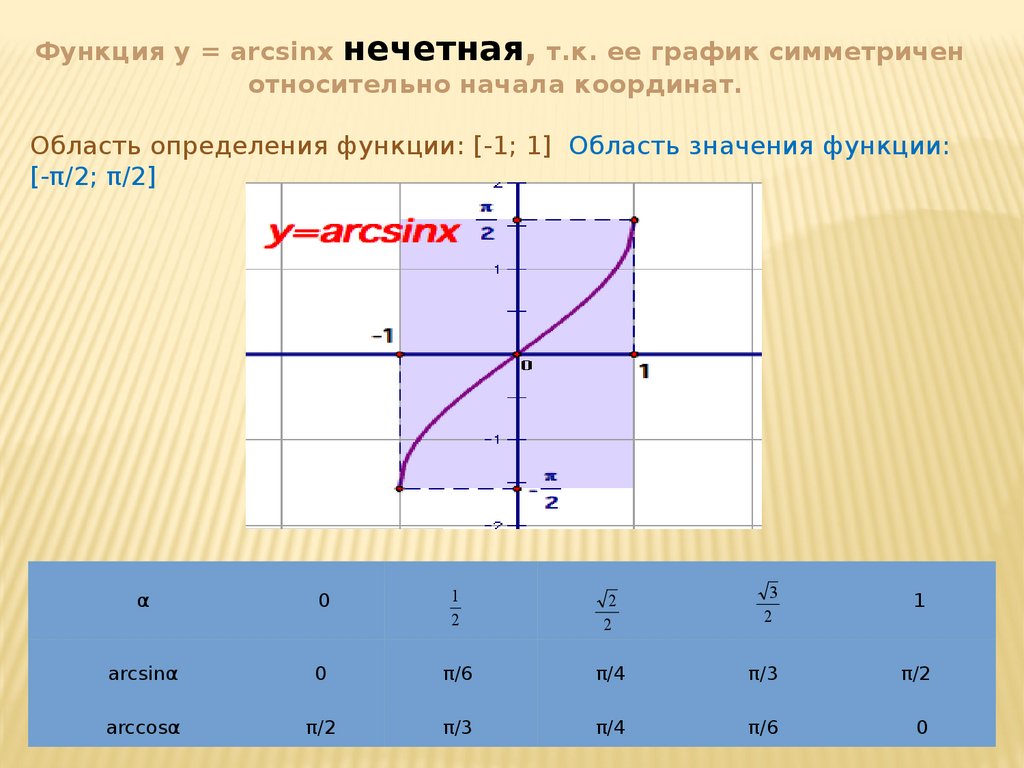
Функция y = arcsinx нечетная, т.к. ее график симметричен
относительно начала координат.
Область определения функции: [-1; 1] Область значения функции:
[-π/2; π/2]
α
 0
arcsinα
0
arccosα
π/2
2
2
3
2
1
π/6 
π/4 
π/3 
π/2 
π/3 
π/4 
π/6 
 0
1
2

4.

Обратные тригонометрические функции
Определениеarccos a
arccos a ( a 1
Аркосинусом числа
из промежутка
косинус которого равен
arccosa
Примеры
называется угол (число)
0; П
0; П
cos a
1 Ï
arccos , arccos( 1) Ï
2 3
arccos
3 П
П
; arccos 0
2
6
2
Функция y = arccosx - общего вида, т.к. arccos(-x) = π - arccosx

5.

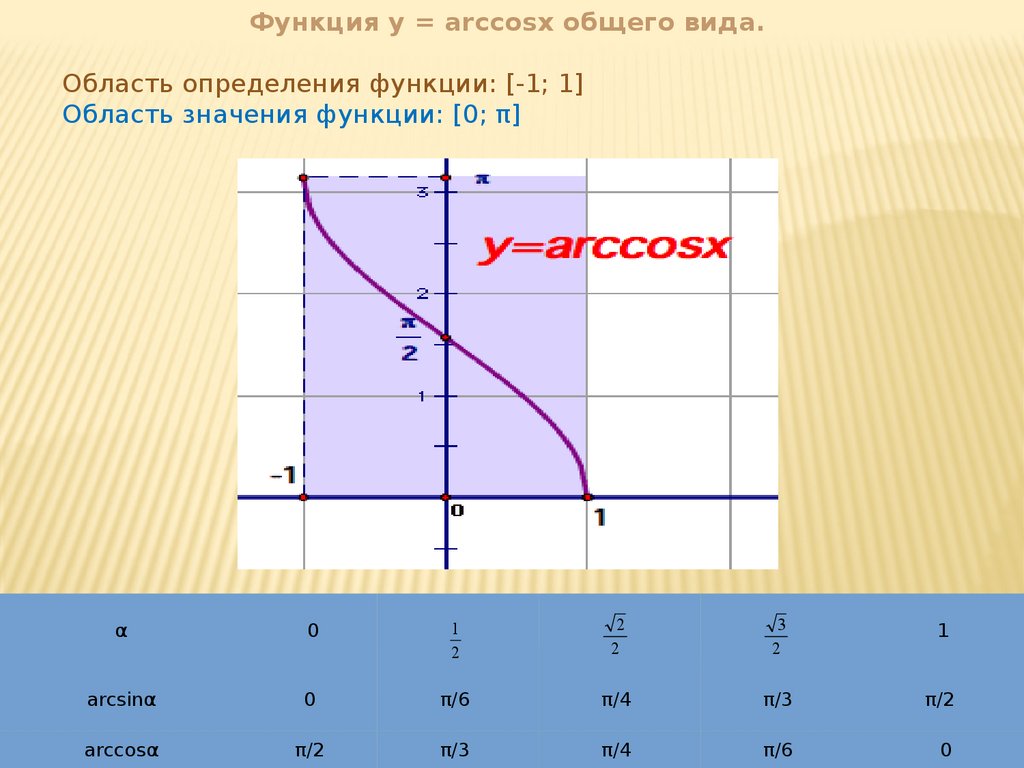
Функция y = arccosx общего вида.
Область определения функции: [-1; 1]
Область значения функции: [0; π]
α
 0
1
2
2
2
3
2
1
arcsinα
0
π/6 
π/4 
π/3 
π/2 
arccosα
π/2
π/3 
π/4 
π/6 
 0

6.

Обратные тригонометрические
функции
arctg
Определение
Арктангенсом числа
называется угол (число) П ; П
2 2
из промежутка
тангенс
которого равен
arctg
arctg 1
Примеры:
arctg
П П
;
2 2
tg
П
П
, arctg ( 3)
4
3
3
П
, arctg 0 0
3
6
Функция y = arctgx - нечетная, т.к. arctg(-x) = - arctgx

7.

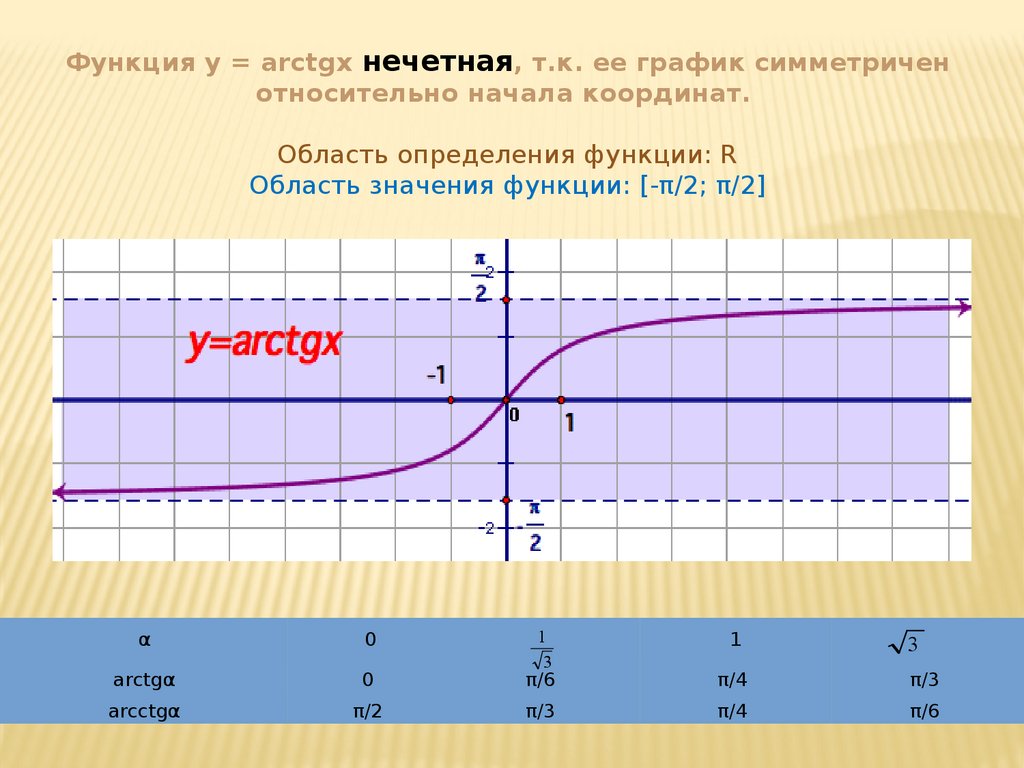
Функция y = arctgx нечетная, т.к. ее график симметричен
относительно начала координат.
Область определения функции: R
Область значения функции: [-π/2; π/2]
1
3
α
 0
1
arctgα
0
π/6 
π/4 
π/3 
arcctgα
π/2
π/3 
π/4 
π/6 
3

8.

Обратные тригонометрические
функцииОпределение
arcctg
Арккосинусом числа
промежутка
котангенс которого равен
arcctg
называется угол (число) из 0; П
0; Ï
ñtg
arcctg
3
П
П
, arcctg 0
3
3
2
arcctg
П
3П
3 , arcctg ( 1)
6
4
Примеры:
Функция y = arctgx - нечетная, т.к. arctg(-x) = - arctgx

9.

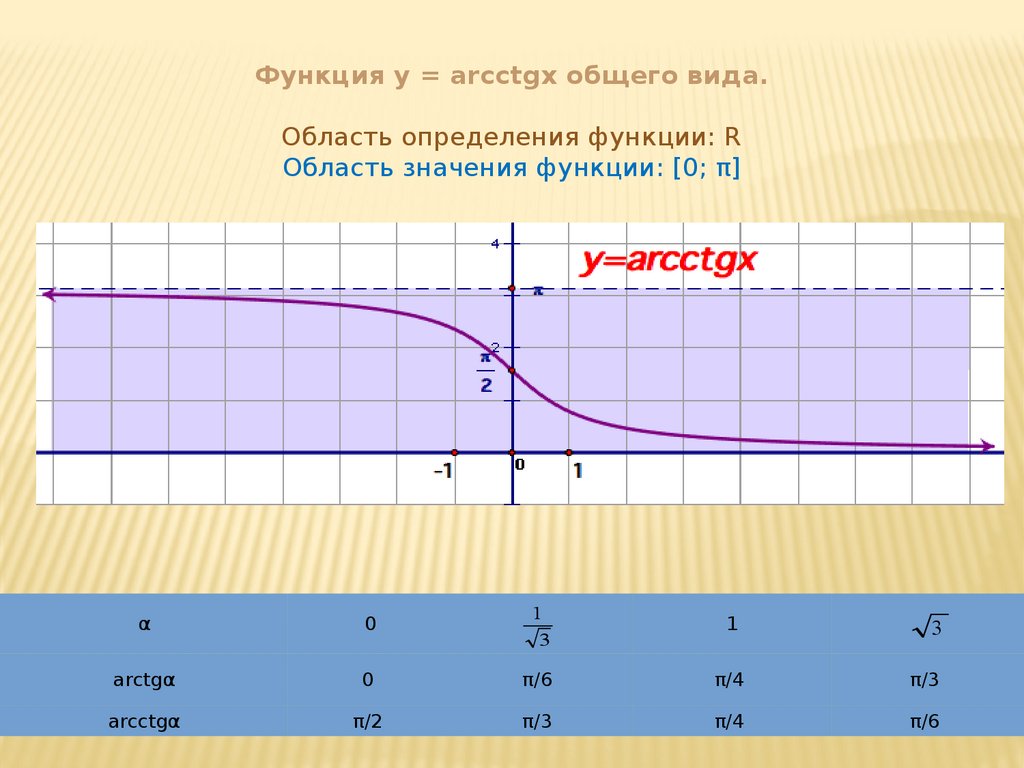
Функция y = arcctgx общего вида.
Область определения функции: R
Область значения функции: [0; π]
α
 0
1
3
1
arctgα
0
π/6 
π/4 
π/3 
arcctgα
π/2
π/3 
π/4 
π/6 
3

10.

Спасибо за работу!