Сила Ампера. Движение заряженных частиц в магнитном поле. Задачи

1.

Задача 1
Задача 7
Задача 2
Задача 8
Задача 3
Задача 9
Задача 4
Задача 10
Задача 5
Задача 11
Задача 6
Задача 12
Теоретическое введение

2.

Сила Ампера. Движение заряженных
частиц в магнитном поле
Магнитная индукция В связана с напряженностью Н магнитного поля соотношением
В = 0Н
Где - относительная магнитная проницаемость среды,
0 - 4 ·10-7 Гн/м=12,57·10-7 Гн/м - магнитная постоянная.
Для ферромагнитных тел = f (Н), следовательно, и B=f(H). При решении задач, где требуется знать
B=f(H), необходимо пользоваться соответствующим графиком.
Объемная плотность энергии магнитного поля
w0
HB
2
Магнитный поток (поток магнитной индукции) сквозь контур
Ф = BS cos
Где S - площадь поперечного сечения контура,
- угол между нормалью к плоскости контура и направлением магнитного поля. Магнитный поток
сквозь тороид:
Ф
0 IN S
L
где N - общее число витков тороида,
L - его длина,
S - площадь поперечного сечения,
- относительная магнитная проницаемость материала сердечника,
0 - магнитная постоянная.

3.

Если тороид имеет воздушный зазор, то
Ф
IN
L1
L2
S 0 1
S 0 2
где L1 - длина железного сердечника,
1 - его магнитная проницаемость,
L2 - длина воздушного зазора,
2 - магнитная проницаемость воздуха.
На элемент dl проводника с током, находящемся в магнитном поле, действует сила Ампера:
dF = BI sin dl
где - угол между направлениями тока и магнитного поля.
На замкнутый контур с током на магнитную стрелку в магнитном поле действует пара сил с
вращающим моментом:
M = pI sin
где
р - магнитный момент контура с током (или магнитной стрелки),
- угол между направлением магнитного поля и нормалью к плоскости контура (или осью стрелки).
Магнитный момент контура с током (по модулю)
p = IS
где S - площадь контура.
Поэтому
M = BIS sin
Два параллельных бесконечно длинных прямолинейных проводника с токами I1 и I2 взаимодействуют между
собой с силой:
L - длина участка проводников,
I1I 2 L
F 0
, d - расстояние между ними.
2 d
Работа по перемещению проводника с током в магнитном поле
dA = IdФ,
где dФ - магнитный поток, пересеченный проводником при его движении.

4.

Сила, действующая на заряженную частицу, движущуюся со скоростью в магнитном поле,
определяется формулой Лоренца
F = qB sin
где
q - заряд частицы,
- угол между направлениями скорости частицы и магнитного поля.
При протекании тока I вдоль проводящей пластины, помещенной перпендикулярно к магнитному полю,
возникает поперечная разность потенциалов
IB
IB
U k
a
nea
1
k
ne
где а - толщина пластины,
В - индукция магнитного поля.
постоянная Холла, обратная концентрации п носителей тока и их заряду е. Зная
постоянную Холла k и удельную проводимость
материала
1
neu,
можно найти подвижность носителей заряда и.
Явление электромагнитной индукции заключается в появлении в контуре э.д.с. индукции при
всяком изменении магнитного потока Ф сквозь поверхность, охватываемую контуром. Э.Д.С. индукции
определяется уравнением:
dФ
E
dt
.
Изменение магнитного потока может достигаться изменением тока в самом контуре (явление самоиндук
При этом Э.Д.С. самоиндукции определяется формулой:
E L
dI
,
dt
где L - индуктивность контура.
Индуктивность соленоида:
L = 0n2IS,
где l - длина соленоида,
S - площадь его поперечного сечения,
п - число витков на единицу его длины.

5.

Вследствие явления самоиндукции при выключении э.д.с. ток в цепи спадает по закону
R
I I 0 exp
L
t ,
а при включении э.д.с. ток нарастает по закону
R
I I 0 1 exp t ,
L
где R - сопротивление цепи.
Магнитная энергия контура с током:
LI 2
W
.
2
Изменение магнитного потока может достигаться также изменением тока в соседнем контуре
(явление взаимной индукции). При этом индуцируемая э.д.с.
E L12
dI
,
dt
где L12 - взаимная индуктивность контуров.
Взаимная индуктивность контуров, пронизываемых общим магнитным потоком
L = 0n1n2IS,
где n1 и п2 - числа витков на единицу длины этих соленоидов.
Количество электричества, прошедшего через поперечное сечение проводника при возникновении в нем
индукционного тока
dq
1
dФ.
R

6.

Задача 1
Между полюсами электромагнита создается однородное магнитное поле с
индукцией В=0,1 Тл. По проводу длиной l=70 см, помещенному
перпендикулярно к направлению магнитного поля, течет ток I=70 А. Найти
силу F, действующую на провод.

7.

Задача 1
Дано:
В=0,1 Тл
l = 0,7 м
I = 70 А
=90
F -?
Решение:
Сила Ампера, действующая на проводник с током в
магнитном поле
F = BIl sin
В данном случае =90°, sin90°=1. С
учетом этого формула приобретает
вид
F = BIl
F=4,9 (Н)
Ответ:
В
I
F
сила, действующая на провод, помещенный между полюсами
электромагнита перпендикулярно к направлению магнитного поля, равна
F=4,9 Н.

8.

Задача 2
Из проволоки длиной l =20 см сделаны квадратный и круговой контуры.
Найти вращающие моменты сил M1 и М2, действующие на каждый контур,
помещенный в однородное магнитное поле с индукцией В=0,1 Тл. По
контурам течет ток I =2 А. Плоскость каждого контура составляет угол 45° с
направлением поля.

9.

Задача 2
Дано:
В=0,1 Тл
l = 0,2 м
I=2А
=45
M1,М2 - ?
В
Решение:
Вращающий момент сил, действующих на контур,
помещенный в однородное магнитное поле
n
M = BIS sin
l2
S
16
Во втором случае длина круга
l = 2 R
1
l2
l2
2
, тогда
Отсюда R
S R 2
. (3)
2
4
4
Подставим (3) и (2) в (1), получаем
BIl 2
BIl2
М1
sin ,
М2
sin ,
16
4
где - угол между направлением
магнитного поля и нормалью к
плоскости контура.
В
I
В
I
n
n
Ответ: вращающие моменты сил M1 и М2, действующие на контуры в
однородном магнитном поле M1=3,53·10-4 Н·м, М2 =4,5·10-2 Н·м.
В
n

10.

Задача 3
Катушка гальванометра, состоящая из N=400 витков тонкой проволоки,
намотанной на прямоугольный каркас длиной l =3 см и шириной b=2 см,
подвешена на нити в магнитном поле с индукцией В=0,1 Тл. По катушке
течет ток I =0,1 мкА. Найти вращающий момент М, действующий на
катушку гальванометра, если плоскость катушки:
а) параллельна направлению магнитного поля,
б) составляет угол =60° с направлением магнитного поля.

11.

Задача 3
Дано:
N=400
В=0,1 Тл
l = 0,3 м
b= 2 см
I = 0,1 мкА
а) =0
б) = 60
M-?
Решение:
M = BIS sin
(1)
Для нахождения в двух случаях, рассмотрим случай
a) =90°-0°=90°,
т.к. нормаль перпендикулярна к плоскости,
которая параллельна направлению магнитного поля.
б) =90°-60°=30°,
т.к. нормаль перпендикулярна к плоскости, которая
составляет угол =60° с направлением магнитного
поля.
М = MN
где М - вращающий момент сил, действующий на каждый виток
М = SBIN sin
Учитывая тот момент, что виток имеет форму прямоугольника, получаем
М = blBIN sin
Ответ:
вращающий момент, действующий на катушку гальванометра в
случае, когда плоскость катушки: а) параллельна направлению
магнитного поля M1 = 2,4·10-9 (Н·м); б) составляет угол =60° с
направлением магнитного поля M2 = 1,2·10-9 (Н·м).

12.

Задача 4
В однородном магнитном поле с индукцией В=0,5 Тл движется равномерно
проводник длиной l=10 см. По проводнику течет ток I=2 А. Скорость
движения проводника = 0,2 м/с и направлена перпендикулярно к
направлению магнитного поля. Найти работу по перемещению проводника за
время t=10 с и мощность Р, затраченную на его перемещение.

13.

Задача 4
Дано:
В=0,5 Тл
l = 0,1 м
= 0,2 м/с
I=2А
A, P - ?
Решение:
- угол между нормалью к плоскости контура и направлением
магнитного поля
cos =1
А = I Ф
A FA S FA S cos BlI S BSI
Ф = BS cos Ф = BS
S' = t
S=l S' = l t
Ф = l tB
(3)
Подставим (3) в (1), получаем
А = I Bl t (4)
Ответ:
B
- угол между направлением действия силы и
перемещением т.е. =0, отсюда cos =l.
FA
l
(1)
I
S
S
(2)
P
A
t
(5)
Подставляем (4) в (5), получаем:
P=BIl
работа по перемещению проводника за время t равна А=0,2 Дж, мощность,
затрачиваемая при этом перемещение равна Р=0,02 Вт.

14.

Задача 5
Электрон, ускоренный разностью потенциалов U=l кВ влетает в однородное
магнитное поле, направление которого перпендикулярно к направлению его
движения. Индукция магнитного поля В=1,19 мТл. Найти радиус R
окружности, по которой движется электрон, период обращения Т и момент
импульса М электрона.

15.

Задача 5
Дано:
Решение:
U=l000В
В=1,19·10-3 Тл
т0 = 9,1·10-31 кг
е
Кл
1,76 1011
т0
кг
F
Л
Частица приобретает кинетическую энергию
m 02
W
2
Согласно закону сохранения и превращения энергии
R
e
В
m 02
2Ue
eU
0
R, T, M - ?
(1)
2
m
Сила Лоренца сообщает заряду перпендикулярное к скорости ускорение
wП
F
e
Это ускорение изменяет лишь направление скорости, величина
B
же скорости остается неизменной. Следовательно, и
m m
m
R
e B
ускорение будет постоянным по величине. При этих условиях
заряженная частица движется равномерно по окружности,
радиус которой определяется соотношением
2
wП
(2)
Подставив (1)в (2), получаем:
Т
2 R
2
R
m
eB
R
2Ue
2Um 1
m
e B
2Um 1 m
m
2Ue 2Um 1
2Um
2
M
m
.
M
=
m
R
е B 2Ue eB
m
e B
B
радиус окружности, по которой движется частица равен R=9 см,
Ответ:
период обращения электрона по этой окружности равен Т=30 нс,
момент
2
24 кг м
М
15
,
10
импульса электрона
с

16.

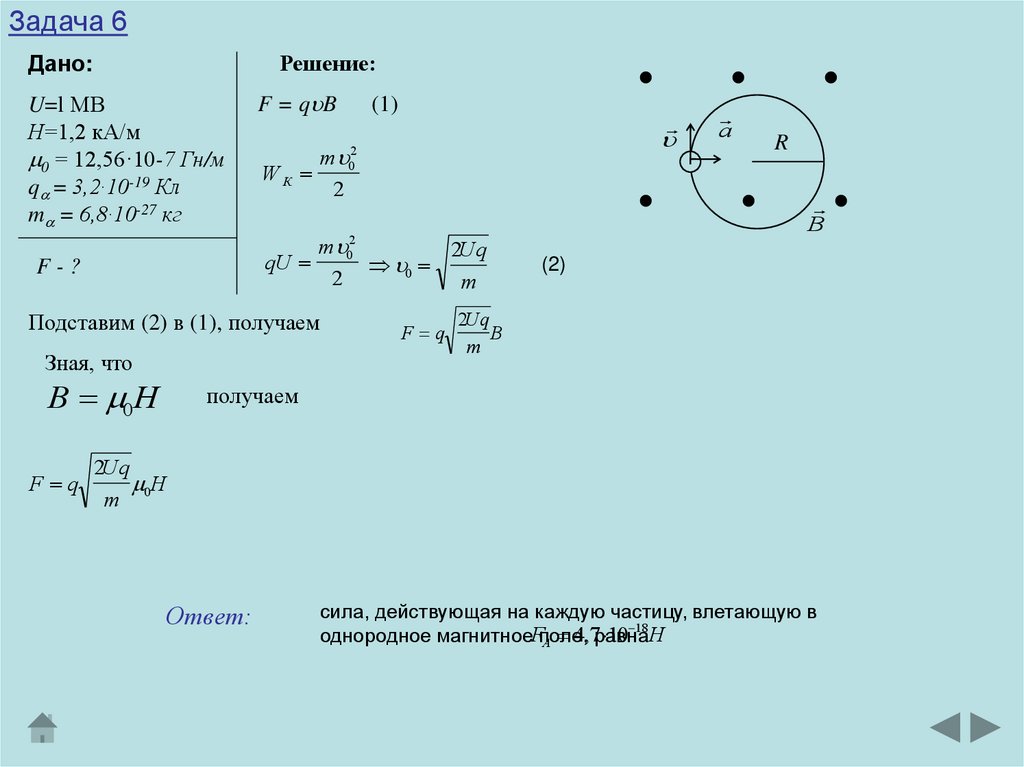
Задача 6
Поток альфа частиц, ускоренных разностью потенциалов U=l MB, влетает в
однородное магнитное поле напряженностью Н=1,2 кА/м. Скорость каждой
частицы направлена перпендикулярно к направлению магнитного поля. Найти
силу F, действующую на каждую частицу.

17.

Задача 6
Дано:
Решение:
U=l МВ
Н=1,2 кА/м
0 = 12,56·10-7 Гн/м
q = 3,2·10-19 Кл
m = 6,8·10-27 кг
F = q B
m 02
WК
2
m 02
2Uq
qU
0
2
m
F-?
Подставим (2) в (1), получаем
Зная, что
B 0H
F q
(1)
F q
а
R
В
(2)
2Uq
B
m
получаем
2Uq
Н
m 0
Ответ:
сила, действующая на каждую частицу, влетающую в
10 18 H
однородное магнитноеFполе,
равна
A 4,7

18.

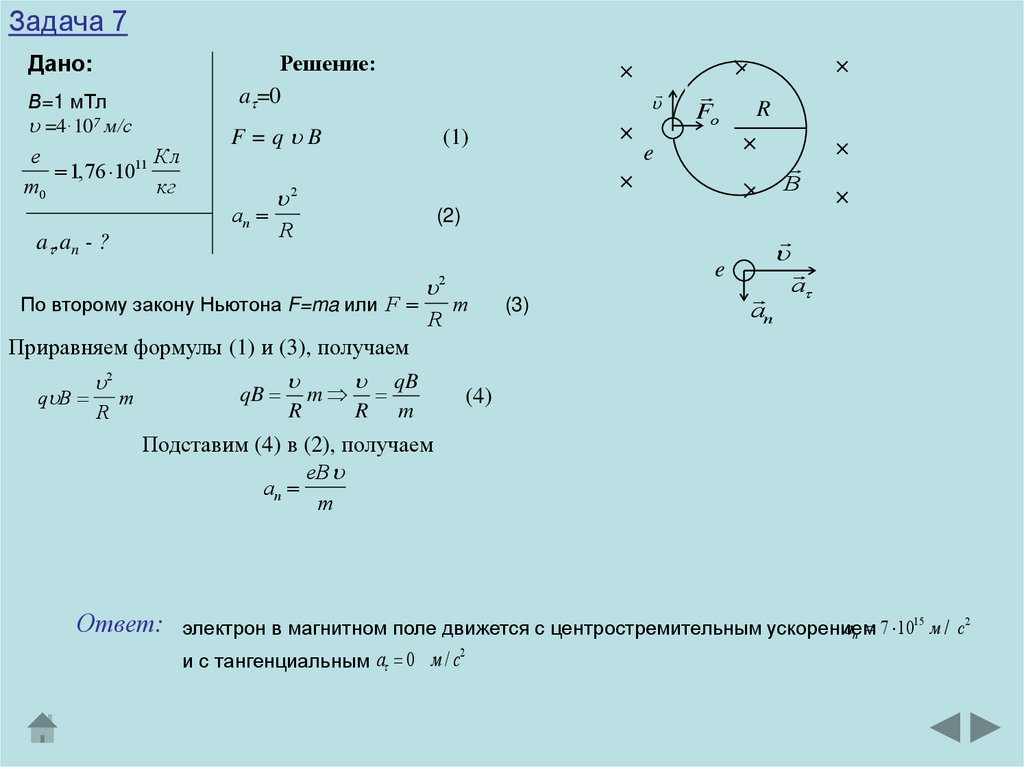
Задача 7
Электрон влетает в однородное магнитное поле, направление которого
перпендикулярно к направлению его движения. Скорость электрона =4·107
м/с. Индукция магнитного поля В=1 мТл. Найти тангенциальное и
нормальное ускорения электрона в магнитном поле.

19.

Задача 7
Дано:
Решение:
a =0
В=1 мТл
=4·107 м/с
е
Кл
1,76 1011
т0
кг
a ,an - ?
F=q B
an
(1)
2
qB
m
R
e
В
2
R
m
R
e
m
Приравняем формулы (1) и (3), получаем
qB
2
R
R
(2)
R
По второму закону Ньютона F=ma или F
q B
Fо
m
(3)
ап
а
(4)
Подставим (4) в (2), получаем
eB
an
m
Ответ:
an 7 1015 м / с2
электрон в магнитном поле движется с центростремительным ускорением
2
и с тангенциальным a 0 м / с

20.

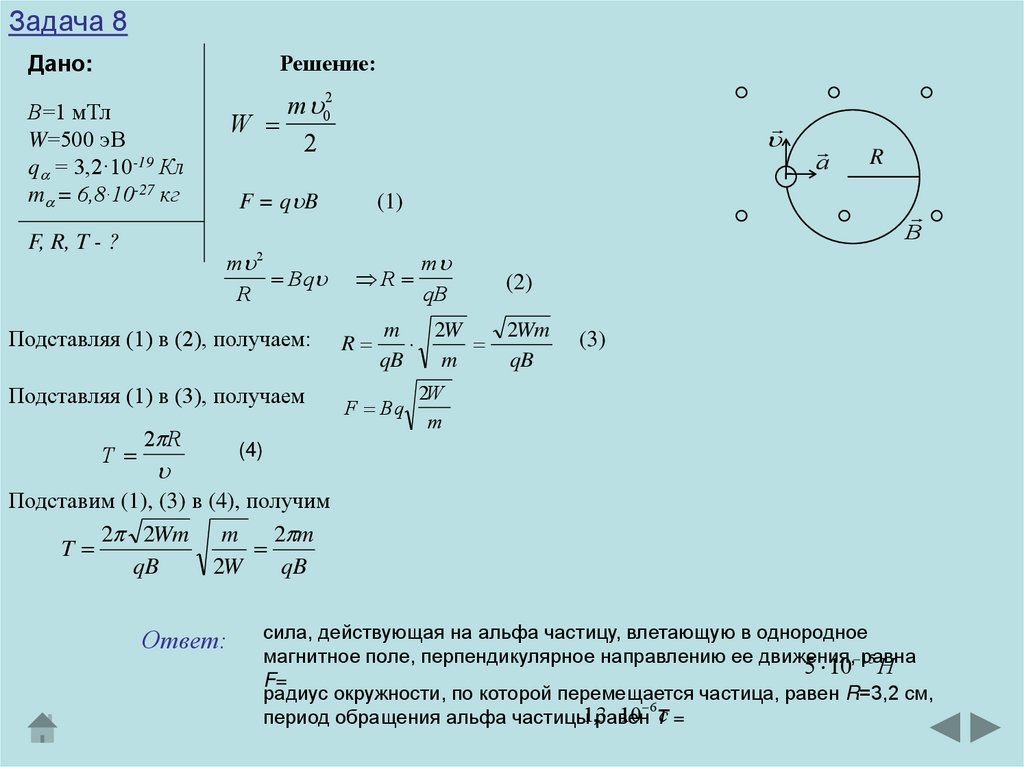
Задача 8
Альфа-частица, кинетическая энергия которой W=500 эВ, влетает в
однородное магнитное поле, перпендикулярное к направлению ее движения.
Индукция магнитного поля В=0,1 Тл. Найти силу F, действующую на альфа
частицу, радиус R окружности, по которой она движется и период обращения
Т альфа-частицы.

21.

Задача 8
Дано:
Решение:
m 02
W
2
В=1 мТл
W=500 эВ
q = 3,2·10-19 Кл
m = 6,8·10-27 кг
F, R, T - ?
F = q B
(1)
m 2
Bq
R
R
Подставляя (1) в (2), получаем:
Подставляя (1) в (3), получаем
T
2 R
R
R
В
m
qB
m
2W
qB
m
F Bq
а
(2)
2Wm
qB
(3)
2W
m
(4)
Подставим (1), (3) в (4), получим
2 2Wm m
2 m
T
qB
2W
qB
Ответ:
сила, действующая на альфа частицу, влетающую в однородное
магнитное поле, перпендикулярное направлению ее движения, 15
5 10 равна
H
F=
радиус окружности, по которой перемещается частица, равен R=3,2 см,
,равен
10 6Тc =
период обращения альфа частицы13

22.

Задача 9
Найти отношение q/m для заряженной частицы, если она, влетая в
однородное магнитное поле с напряженностью Н=200 кА/м со скоростью
106 м / с движется по дуге окружности радиусом R=8,3 см.
Направление движения частицы перпендикулярно к направлению
магнитного поля. Сравнить значение со значением q/m для электрона,
протона и альфа частицы.

23.

Задача 9
Дано:
Решение:
Н=200 кА/м
106 м / с
R=8,3 см
= 90°
0 = 12,56·10-7 Гн/м
R
an
F
q/m - ?
qB
Т.к. =const, то
F = q B.
(1)
m
B 0H
q
m BR
2
R
2
R
m
(2)
Приравняв выражения (1) и (2), получаем
2
q B m
R
(4)
Ответ:
(3)
q
m 0 HR
отношение q
m
q
m
Кл
кг
для альфа частицы составляет 4,8 107

24.

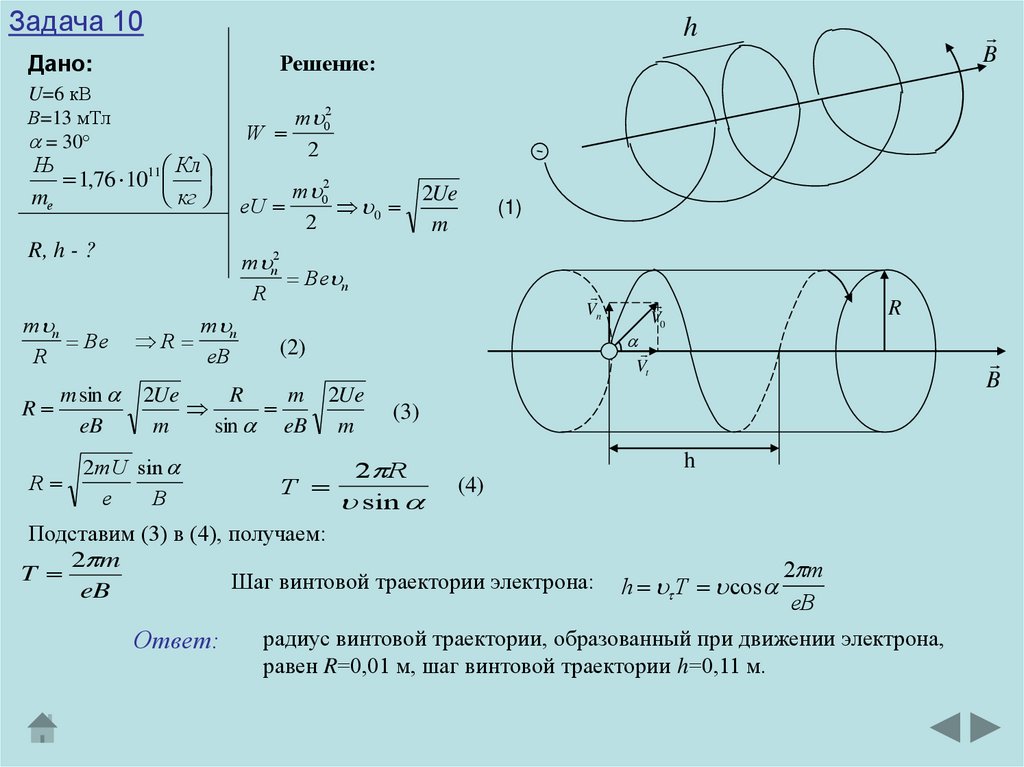
Задача 10
Электрон, ускоренный разностью потенциалов U=6 кВ, влетает в однородное
магнитное поле под углом 30 градусов к направлению поля и движется по
винтовой траектории. Индукция магнитного поля В=13 мТл. Найти радиус R
и шаг h винтовой траектории.

25.

Задача 10
Дано:
Њ
Кл
1,76 1011
mе
кг
R, h - ?
R
m sin
eB
B
Решение:
U=6 кВ
В=13 мТл
= 30°
m n
Be
R
h
m 02
W
2
m 02
2Ue
eU
0
2
m
m n2
Be n
R
m n
R
eB
Vn
(2)
2Ue
R
m 2Ue
m
sin eB m
2mU sin
R
e
B
(1)
R
Vt
B
(3)
2 R
(4)
T
sin
Подставим (3) в (4), получаем:
2 m
T
Шаг винтовой траектории электрона:
eB
Ответ:
V0
h
h T cos
2 m
eB
радиус винтовой траектории, образованный при движении электрона,
равен R=0,01 м, шаг винтовой траектории h=0,11 м.

26.

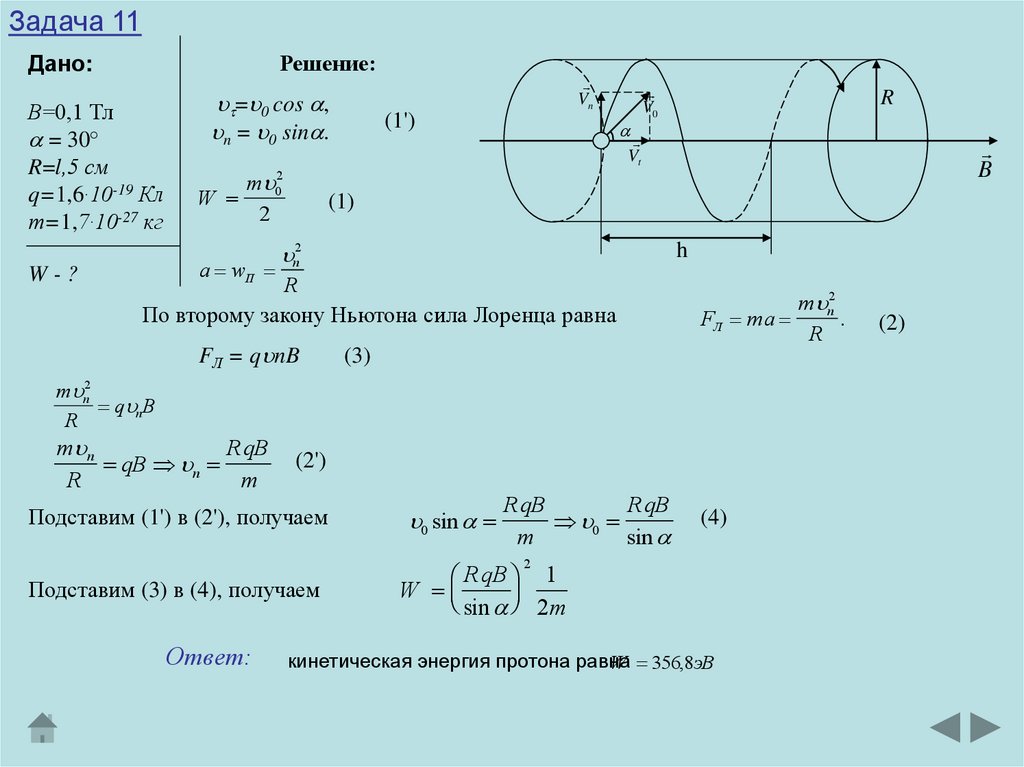
Задача 11
Протон влетает в однородное магнитное поле под углом 30 градусов к
направлению поля и движется по винтовой линии радиусом R=l,5 см.
Индукция магнитного поля В=0,1 Тл. Найти кинетическую энергию W
протона.

27.

Задача 11
Дано:
Решение:
В=0,1 Тл
= 30°
R=l,5 см
q=1,6·10-19 Кл
т=1,7·10-27 кг
= 0 cos ,
n = 0 sin .
m 02
W
2
а wП
W-?
Vn
(1')
V0
R
Vt
B
(1)
n2
h
R
По второму закону Ньютона сила Лоренца равна
FЛ = q nB
m n2
FЛ ma
.
R
(3)
m n2
q n B
R
m n
RqB
qB n
R
m
(2')
Подставим (1') в (2'), получаем
0 sin
RqB
RqB
0
m
sin
(4)
2
Подставим (3) в (4), получаем
Ответ:
R qB 1
W
sin 2m
кинетическая энергия протона равна
W 356,8эВ
(2)

28.

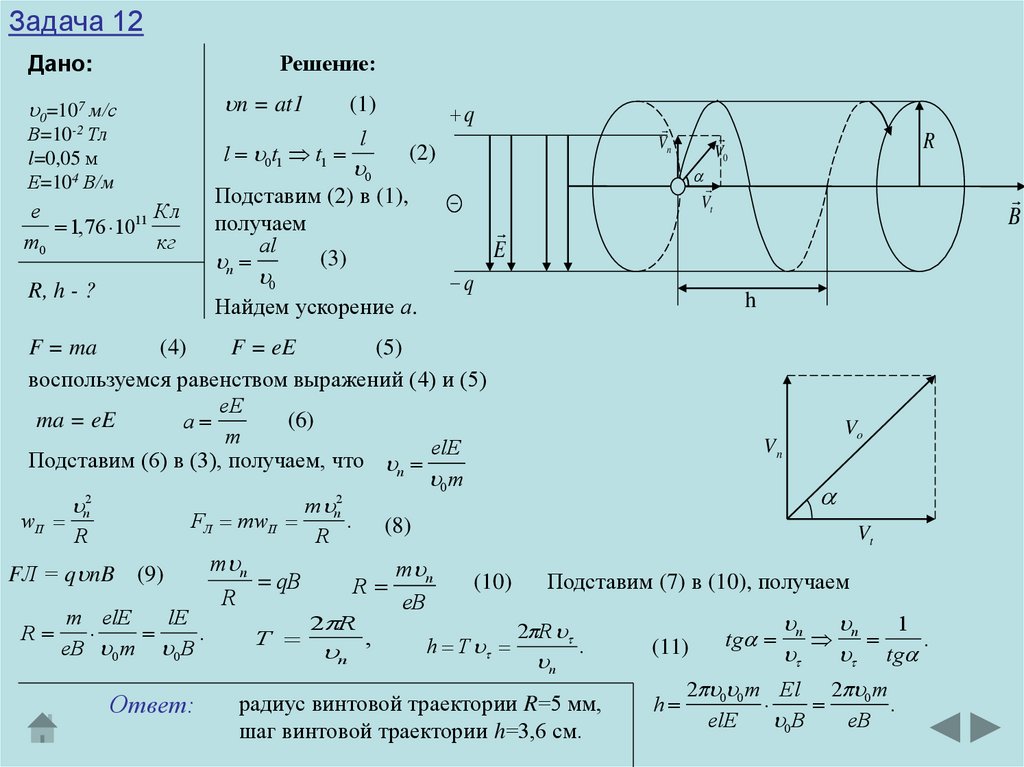
Задача 12
Электрон влетает в плоский горизонтальный конденсатор параллельно
пластинам со скоростью 0=107 м/с. Длина конденсатора l=0,05 м.
Напряженность электрического поля конденсатора Е=10 кВ/м. При вылете из
конденсатора электрон попадает в магнитное поле, перпендикулярное к
электрическому полю. Индукция магнитного поля В=10 мТл. Найти радиус R
и шаг h винтовой траектории электрона в магнитном поле.

29.

Задача 12
Дано:
Решение:
n = at1
0=107 м/с
В=10-2 Тл
l=0,05 м
Е=104 В/м
е
Кл
1,76 1011
т0
кг
R, h - ?
(1)
q
l
(2)
l 0t1 t1
0
Подставим (2) в (1),
получаем
al
E
(3)
n
0
q
Найдем ускорение а.
Vn
R
(9)
m elE
lE
.
eB 0 m 0 B
Ответ:
m n
qB
R
T
R
2 R
п
,
m n
eB
(10)
h T
R
Vt
B
h
F = ma
(4)
F = eE
(5)
воспользуемся равенством выражений (4) и (5)
eE
ma = eE
(6)
а
m
elE
Подставим (6) в (3), получаем, что n
0 m
2
2
m n
wП n
FЛ mwП
.
(8)
R
R
FЛ = q nB
V0
Vo
Vn
Vt
Подставим (7) в (10), получаем
2 R
n
.
радиус винтовой траектории R=5 мм,
шаг винтовой траектории h=3,6 см.
(11)
h
tg
n
1
n
.
tg
2 0 0 m El 2 0 m
.
elE
0 B
eB