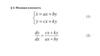Тренинговая работа №4

1. Тренинговая работа №4

Работа учителя математики
Моисеевой Нины Ивановны

2. В12

T 275
100% 45%
T
1
1
T 275
20 9;
T
1
1
(T 275) 20 9T ;
1
:5
1
20 T 275 20 9T ;
1
1
20 T 9T 275 20;
1
1
11 T 275 20;
1
T 500
1
Ответ: 500

3.

16
R
220
R
220
13,75
16
Ответ:13,75

4. B12

Зазор - это то расстояние, которое оставляют между рельсами, для того, чтобы они могли
расширяться при нагревании, возникающего при прохождении поезда по рельсам.
Выразим зазор в метрах: 12 мм = 0,012 = 12 · 10-3 м.
Раскроем скобки: l ( t ) l l t
0
o
0
0
l ( t ) l зазор - длина рельса при удлинении после нагревания на t°.
0
0
25 1,2 10 t 12 10
5
l l t l зазор
0
0
0
3
0
l t зазор
0
0
0
12 10
t
;
25 1,2 10
Ответ: 40
3
0
5
t 40
0

5. В13

Пусть х км/ч - скорость 2 автомобиля,
S
1автомо
биль
2автомо
биль
420
420
v
х+10
х
t
t
1
t
2
тогда (х+10)км/ч-скорость первого автомобиля.
S
S v t t ;
v
420
x 10
t1 < t2
420
x
=> t1 + 1 = t2
x 10 x 4200 0;
2
420
420
1
;
x 10
x
420 x x 10 x 420( x 10);
2
x 70;
1
x 60.
1
420 x x 10 x 420 x 4200;
2
Пос. корень (скорость положительное число)
Ответ: 60

6.

S
v
По
течению
24
Х+3
Против
течения
24
Х-3
t
24
X 3
24
X 3
Х км/час = скорость лодки
в неподвижной воде
S
S = 24км S v t t
v
20мин = 1/3 часа.
24
24
1
=
, Общий знаменатель: 3(Х-3)(Х+3)
X 3
X 3 3
24·3(Х+3) = 24·3(Х-3) + (Х-3)·(Х+3); 9(24 + 24 + 1)= Х2;
24·3Х + 24·9 = 24·3Х - 24·9 + Х2-9;
24·9 + 24·9 + 9=
Х2;
9 · 49 = Х2;
Х = 3·7;
Х = 21
Ответ: 21

7. B13

Пусть Х волков в 1 заповеднике, тогда У волков во 2 заповеднике.
В двух заповедниках 220 особей.
Через год в 1 заповеднике стало Х +0,1Х = 1,1Х волков
_
Х + У = 220
1,1Х + 1,2У = 250
А во 2 заповеднике стало У + 0,2У = 1,2У
В двух заповедниках через год уже 250 особей.
Х + У = 220
Х + 2У = 300
Х + У = 220
У = 80
0,1Х + 0,2У = 30 · 10
Х = 140
Можно решать систему
и методом подстановки.
Ответ: 140

8. В13

Первая труба пропускает на 3 л воды в минуту меньше, чем вторая.
Сколько литров воды в минуту пропускает вторая труба, если резервуар
объемом 648 л она заполняет на 3 минуты быстрее, чем первая труба?
Пусть х литров воды в минуту пропускает вторая труба, тогда
(х – 3) литров воды в минуту пропускает первая труба.
648
время, за которое резервуар объемом 648 л заполняет вторая труба.
x
648
время, за которое резервуар объемом 648 л заполняет первая труба.
x 3
648
648
3
;
x
x 3
648( x 3) 3( x 3 x ) 648 x;
2
648 x 3 648 3 x 9 x 648 x;
2
3 x 9 x 3 648 0;
2
x 3 x 648 0;
2
:3
648 x 3 648 3 x 9 x 648 x;
2
x 27;
x 24( постор .корень)
Ответ: 27

9. В13

Ежемесячный доход семьи складывается из зарплаты отца и зарплаты матери.
Зарплату отца увеличили на 5%, а зарплату матери – на 75%, в результате чего
семейный доход увеличился на 15%. Во сколько раз зарплата матери до повышения
была меньше зарплаты отца?
Общий доход семьи: Доход семьи после увеличения на 15%
X - заработок отца
100%+5%=105%
1,05 Х -заработок отца
У - заработок матери 100%+75%=175% 1,75 У -заработок матери
Х+У
1,05Х + 1,75У
семейный доход увеличился на 15%
1,15(Х + У) = 1,05Х + 1,75У
1,15Х +1,15У = 1,05Х + 1,75У
1,15Х - 1,05Х = 1,75У - 1,15У
0,1Х = 0,6У
Х = 6У
зарплата матери до повышения была меньше зарплаты отца в 6 раз
Ответ: 6

10. В14

y 8tgx 8 x 2 5;
1
y 8
8;
cos x
2
y 0,
8 8 cos x
y
;
cos x
2
2
1 cos x 1
0 cos x 1;
2
8 8 cos x 0
2
8 8 8 8 cos x 0 8
0 8 8 cos x 8
0 y 8
у´ > 0 => функция на всей области
определения возрастает.
Следовательно в точке
x
4
функция имеет наименьшее значение.
y 8tg 8 2 5;
4
4 4
y 8 2 2 5;
4
y 3;
4
Ответ: -3

11.

y = 5cosx – 6x + 4;
y´ = -5sinx – 6;
y´ ˂ 0;
-5sinx – 6 ˂ 0 т.к.;
1 sin x 1 ( 5)
Следовательно для нахождения наименьшего
значение функция
достаточно вычислить значение функции в точке 0
y(0) 5 cos 0 6 0 4
y ( 0) 5 1 4
y ( 0) 9
5 5 sin x 5 6
5 6 5 sin x 6 5 6
Ответ: 9
11 5 sin x 6 1
Если во всех точках открыто промежутка Х выполняется
неравенство f ´≤0, то функция у = f(х) убывает на промежутке Х

12. B14

y 3 x 6 x 9;
2
y 0
3 x 6 x 9 0;
2
x 2x 3 0
2
x 1,
1
x 3.
2
f ( 1) ( 1) 3 ( 1) 9 ( 1) 29 34
3
2
f ( 3) 27 3 9 27 29 2
f (4) 64 48 36 29 9
Ответ:-2

13. В14

Найдите наибольшее значение функции
у ln( x 6) 9 x на отрезке - 5,5; 0 .
9
ОДЗ: х + 6 > 0 => х > -6. Отрезок [-5,5; 0] принадлежит области допустимых значений
Используем свойство логарифмов:
у 9 ln( x 6) 9 x
-6
х
-5,5
0
Производная натурального логарифма определяется так:
( x 6)
1
9;
y 9
9;
x 6
x 6
9 9 x 54
45 9 x
y 0;
y
; y
;
x 6
x 6
y 9
х +6 = 0
9 x 45;
45 9 x 0;
y( 5) ln( 5 6) 9 ( 5);
9
x 5;
y( 5) 0 45 45.
y( 5,5) ln( 5,5 6) 9 ( 5,5);
y( 5,5) 9 ln(0,5) 49,5.
y(0) ln(0 6) 9 0;
y(0) 9 ln 6.
9
9
Ответ: 45