Похожие презентации:
Фазовая плоскость (§4-7)
1.
§ 4. Фазовая плоскостьx ax by
y cx ky
(1)
dy cx ky
dx ax by
(2)
2.
x(t ) x0 ; y(t ) y0Такое решение называется стационарным решением или стационарным
режимом.
x0 ; y0 точка покоя или положение равновесия системы (1).
ax0 by0 0
cx0 dy0 0
(3)
3.
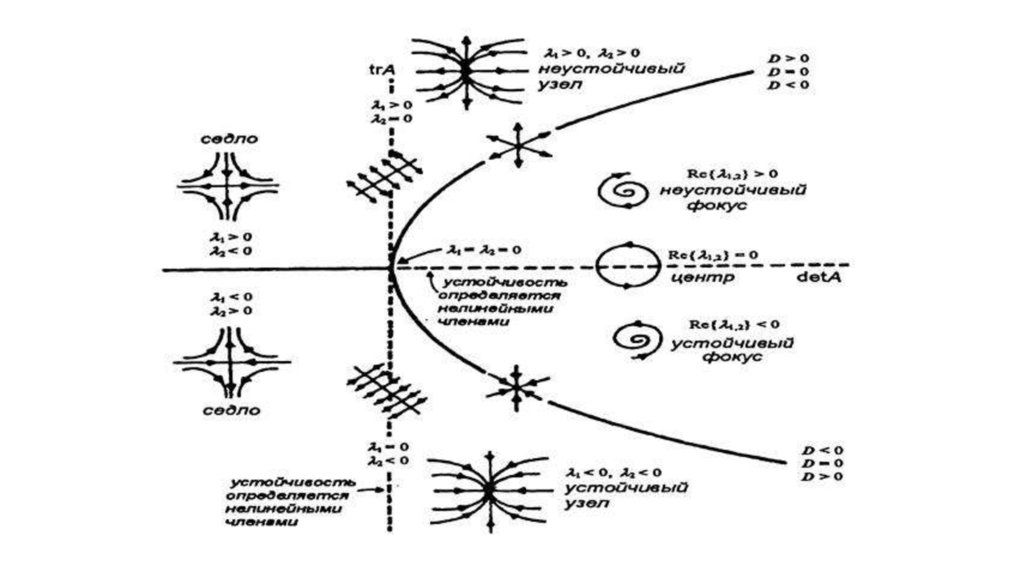
1. Числа 1 и 2 вещественны, различны и имеют один и тот жезнак. Простой узел.
2. Числа 1 и 2 вещественны и имеют разные знаки. Седло.
3. Числа 1
и 2 образуют комплексно-сопряжённую пару с
ненулевой вещественной частью. Фокус.
4. Числа 1и 2 образуют комплексно-сопряжённую пару с нулевой
вещественной частью.
Центр.
5. 1 2 0 . Вырожденный узел или особый узел.
6. Одно или оба числа 1 и 2 равны нулю (для этого снимем
условие det A 0).
4.
6) Далее будем рассматривать вырожденную матрицу AЕсли она имеет вид
a b
то вместо системы (4) для определения
A
ka kb
положений равновесия получим одно уравнение
ax by 0
Это уравнение определяет прямую, проходящую через начало координат.
Каждая точка этой прямой будет положением равновесия; заметим, что
положения равновесия в этом случае не будут являться изолированными.
dy
k ;
Уравнение фазовых траекторий примет вид
dx
оно не имеет особенностей в начале координат.
следовательно, фазовыми траекториями будут параллельные прямые
линии, семейство этих линий определяется уравнением y kx C
5.
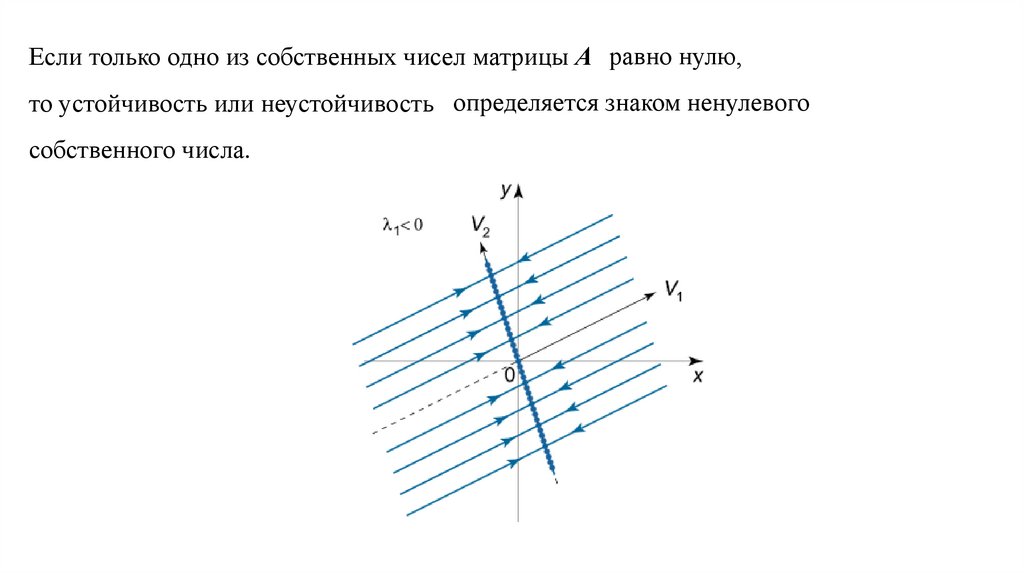
Если только одно из собственных чисел матрицы А равно нулю,то устойчивость или неустойчивость определяется знаком ненулевого
собственного числа.
6.
Если нулю равны оба собственных числа матрицы А то её жорданова форма может иметь вид0 0
J
0 0
x 0
y 0
Уравнение фазовых траекторий
не определяется.
Любая точка фазовой плоскости является
положением равновесия.
Все положения равновесия
x x0 ; y y0
устойчивы, но не являются асимптотически
устойчивыми.
0 1
J
0 0
Уравнение фазовых траекторий:
y 0
Фазовыми траекториями будут прямые, параллельные
оси Ox
Положения равновесия занимают прямую линию
y 0 и неустойчивы.
7.
8.
§ 5. Фазовые траектории нелинейных системx P( x; y )
.(1)
y
Q ( x; y )
dy
Q(x;y)
=
P(x;y)
dx
P(x;y), Q(x;y)
P( x0 ; y0 ) 0
(3)
Q( x0 ; y0 ) 0
(2)
C1(D)
x(t ) x0 ; y(t ) y0
(4)
9.
u x x0 ; v y y0(5)
P
P
u x x 0 P( x; y ) P( x0 ; y0 )
( x x0 )
( y y0 ) l1 ( x x0 ; y y0 )
x
y
P
P
u (t )
v(t ) l1 (u (t ); v(t )).
x
y
Q
Q
v y y 0 Q( x; y ) Q( x0 ; y0 )
( x x0 )
( y y0 ) l2 ( x x0 ; y y0 )
x
y
Q
Q
u (t )
v(t ) l2 (u (t ); v(t )).
x
y
10.
PP
a;
b;
x
y
Q
Q
c;
k.
x
y
u au (t ) bv(t ) l1 (u; v)
v cu (t ) kv(t ) l2 (u; v)
(6)
11.
u au (t ) bv(t )v cu (t ) kv(t )
li (u; v)
u v
2
2
u
2
2 0; i 1;2
v 0
a b
0
det E
c k
(7)
(8)
(9)
12.
§ 6. Линейные системы с периодическими коэффициентамиX A(t ) X
A(t ) A(t )
0
(1)
t ( ; )
Y (t ) A(t )Y (t )
Y (t ) A(t )Y (t ) A(t )Y (t )
13.
Y (t ) Y (t ) DУказанная матрица D называется основной матрицей или
матрицей монодромии.
Введём далее квадратную матрицу S(t), определённую и
непрерывно дифференцируемую на всей вещественной оси и
удовлетворяющую условиям
14.
S (t ) S (t )S (t ) m1
S (t ) m2
det S (t ) m3 0
Такая матрица называется матрицей Ляпунова.
15.
Линейное преобразованиеZ S (t ) X
(2)
называется преобразованием Ляпунова
Z S (t ) X S (t ) X S (t ) S 1 (t ) Z S (t ) A(t ) X S (t )S 1 (t )Z S (t ) A(t )S 1 (t )Z B(t )Z
1
B(t ) S (t ) S (t ) A(t ) S (t )
B(t ) B(t )
16.
Введём матрицу(t ) S (t )Y (t )
(3)
Убедимся, что (t ) - фундаментальная матрица системы
Z B(t ) Z
(4)
1
B(t ) S (t ) S (t ) A(t ) S (t )
17.
S (t )Y S (t )Y S (t )S 1 (t ) S (t ) A(t )Y S (t )S 1 (t ) S (t ) A(t )S 1 (t ) B(t )(t ) S (t )Y (t ) S (t )Y (t ) D (t ) D
Итак, если системы (1) и (4) связаны преобразованием Ляпунова, то их
фундаментальные матрицы связаны соотношением (3) и имеют одну и ту
же основную матрицу.
18.
(1)X A(t ) X
Z B(t ) Z
A(t ) A(t )
B(t ) B(t )
Y (t )
(t )
Y (t ) Y (t ) D
(t ) (t ) D
(4)
Рассмотрим произведение следующих двух матриц
(t )Y (t ) (t ) DD Y (t ) (t )Y (t )
1
1
1
1
19.
1S (t ) (t )Y (t )
(t ) S (t )Y (t )
(3)
Матрица S(t) будет матрицей Ляпунова
Итак, если две линейные системы с периодическими
матрицами одинакового периода
таковы, что
фундаментальные матрицы этих двух систем имеют
одну и ту же основную матрицу, то две указанные
системы
Ляпунова.
связаны
некоторым
преобразованием
20.
Теорема Ляпунова-Флоке.Всякая система (1) с вещественной периодической матрицей A(t)
периода
некоторым вещественным преобразованием Ляпунова
приводится к стационарной системе.
Доказательство.
Пусть
Y (t ) A(t )Y (t )
Y (t ) Y (t ) D
21.
Введём постоянную матрицуA соотношением
( 1)
A LnD
p 1 p
1
1
p 1
e
A
D
D E
p
Рассмотрим линейную стационарную систему
Z A Z
(t ) e
At
(t ) e
(5)
A (t )
e e
At
A
(t ) D
22.
AСобственные числа
матрицы
(характеристические показатели)
j
связаны с собственными числами j матрицы
(мультипликаторами)
соотношением
j
1
Ln j
D
ln i arg 2 ki
1
j
j
i 1.
Из этого соотношения вытекает, что система (1) асимптотически устойчива тогда
и только тогда, когда все её мультипликаторы на комплексной плоскости
расположены внутри окружности единичного радиуса. Система (1) неустойчива
тогда и только тогда, когда хотя бы один её мультипликатор лежит вне указанной
окружности.
23.
§ 7. Построение периодических решений в виде рядовx p1x p2 x f (t )
f (t 2 ) f (t )
Замечание.
2
t ( ; )
t
(1)
24.
a0f (t ) ak cos kt bk sin kt
2 k 1
ak
1
2
f (t ) cos ktdt;
0
bk
1
(2)
2
f (t ) sin ktdt.
0
2
Поставим задачу: выяснить, при каких условиях уравнение (1) будет иметь
периодические решения и сколько таких решений будет. Будем искать такое решение
методом неопределённых коэффициентов, а именно, в виде ряда, аналогичного ряду (2)
25.
A0x(t )
Ak cos kt Bk sin kt
2 k 1
(3)
Подставим ряд (3) в уравнение (1) с учётом разложения (2) и приравняем
слева и справа коэффициенты при одинаковых синусах и косинусах.
k Ak cos kt Bk sin kt p1 k Ak sin kt Bk cos kt
2
k 1
k 1
a
A0
0
ak cos kt bk sin kt .
Ak cos kt Bk sin kt =
+ p2
2 k 1
2 k 1
26.
Тогда для коэффициентовсоотношения
a0
A0 ;
p2
разложения
p2 k 2
pk
1
(3)
получим
следующие
p1k Ak ak
.
2
p2 k Bk bk
(k ) ( p2 k ) p1k
2
2 2
(k ) 0 p2 k ; p1 0 .
2
(4)
27.
28.
a0A0 ;
p2
(k ) 0
x xчастн (t )
p2 0
A0
x(t )
Ak cos kt Bk sin kt
2 k 1
x xчастн (t ) C1e
1t
C2 e
p1 p2 0
2
2 t
29.
Пример 1.x 3x 1 sin t
a0 2; b1 1; p1 0; p2 3;
2
A0 ;
3
3 1 0 A1 0
.
0 3 1 B1 1
2 1
x(t ) sin t
6 2
1
A1 0; B1
2
30.
(k ) 0a0
A0 ;
p2
p2 0
a0 0
x p1x ak cos kt bk sin kt
(5)
k 1
p1 0
2
C2 0
x xчастн (t ) C1 C2e p1t
p1 0
x xчастн (t ) C1 C2t
p1 0)
x xчастн (t ) C1
31.
(k ) 0a0
A0 ;
p2
p2 0
a0 0
a0
x p1x ak cos kt bk sin kt
2 k 1
a0
x p1x 2
a0t
x (t )
2 p1
(0)
32.
2 2(
k
)
(
p
k
) p1k
Перейдём к рассмотрению случая, когда величина
2
2
обращается в ноль при некотором натуральном значении k
( k0 ) 0
k0 N
a
2
x k0 x 0 ak cos kt bk sin kt
2 k 1
(6)
Имеет место резонанс
k k0
0 0 Ak 0 ak 0
.
0 0 Bk 0 bk 0
(7)
33.
a b 02
k0
2
k0
системе (7) удовлетворяют любые два числа.
ak 0 cos k0t bk 0 sin k0t
резонирующие слагаемые отсутствуют
x xчастн (t ) C1 cos k0t C2 sin k0t
Пример 2.
x x cos 2t
(k ) ( p2 k 2 ) 2 p1k
2
a1 b1 0
(1) 0
1
x(t ) cos 2t C1 cos t C2 sin t
3
34.
a b 02
k0
системе (7) не удовлетворяют никакие два числа
2
k0
0 0 Ak 0 ak 0
.
0 0 Bk 0 bk 0
ak 0 cos k0t bk 0 sin k0t
резонирующие слагаемые присутствуют
x k x ak 0 cos k0t bk 0 sin k0t
2
0
t ak 0 cos k0t bk 0 sin k0t
35.
Пример 3.x x cos t
(1) 0
a1 1 0
1
x(t ) t sin t C1 cos t C2 sin t
2
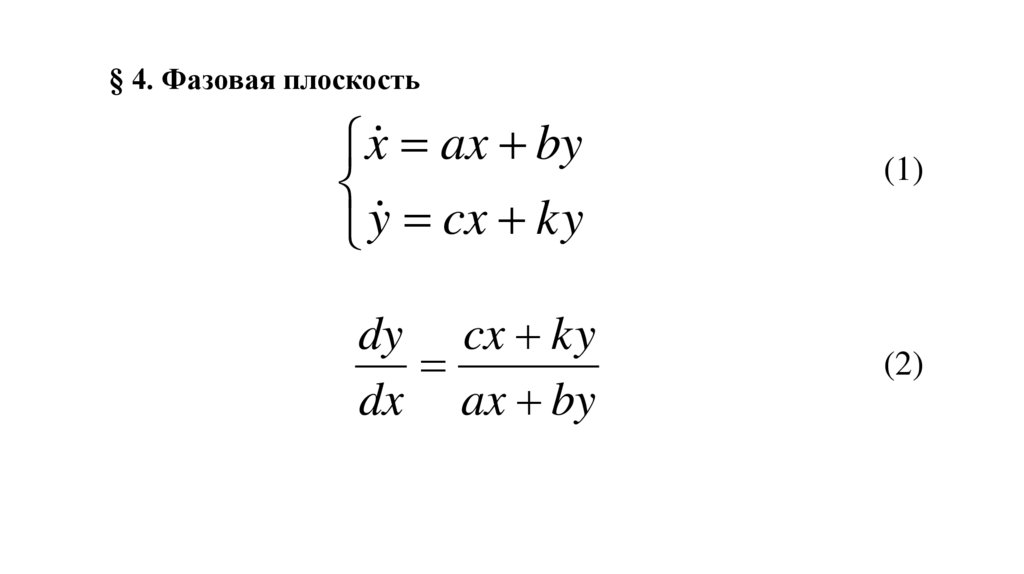





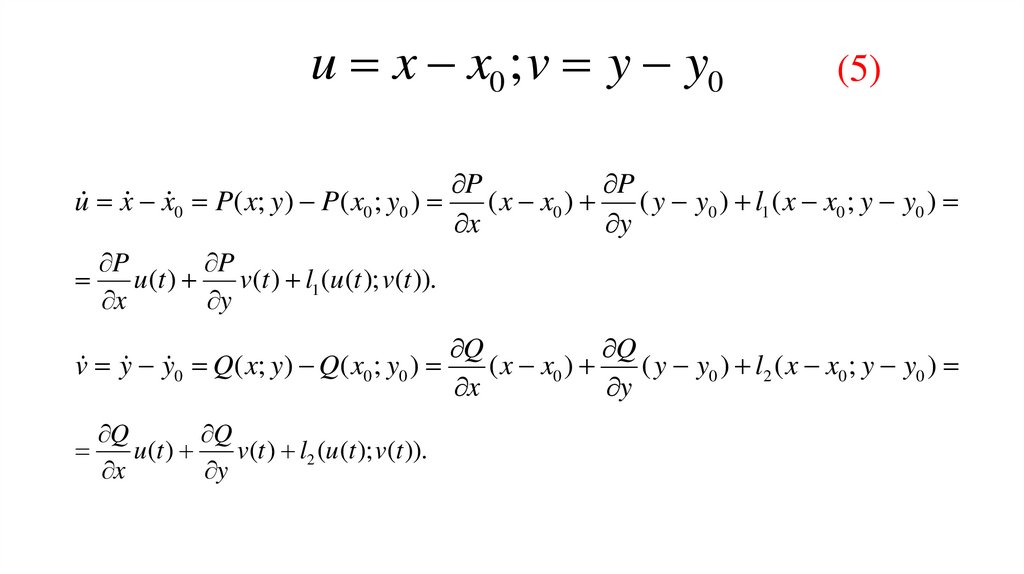
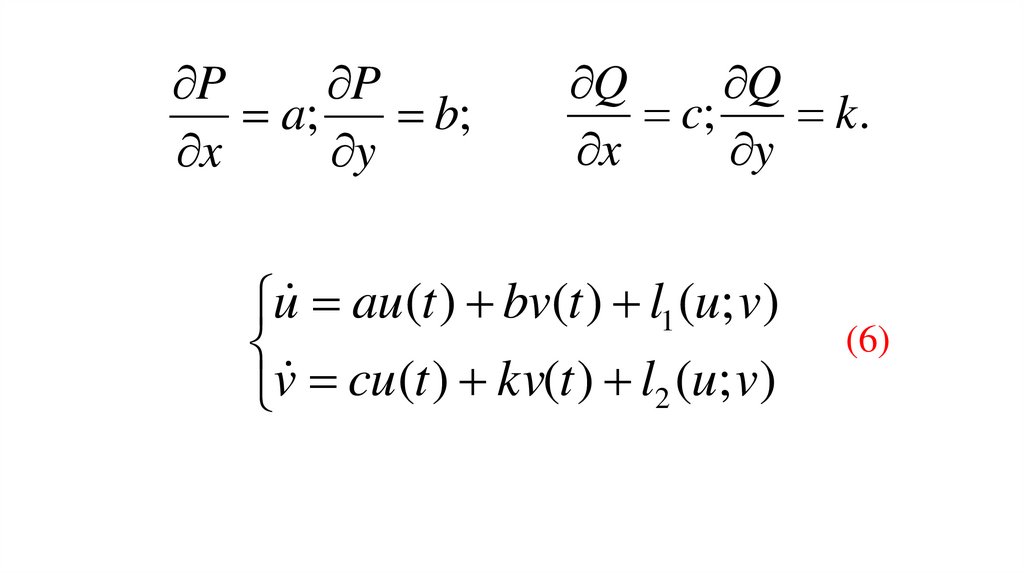
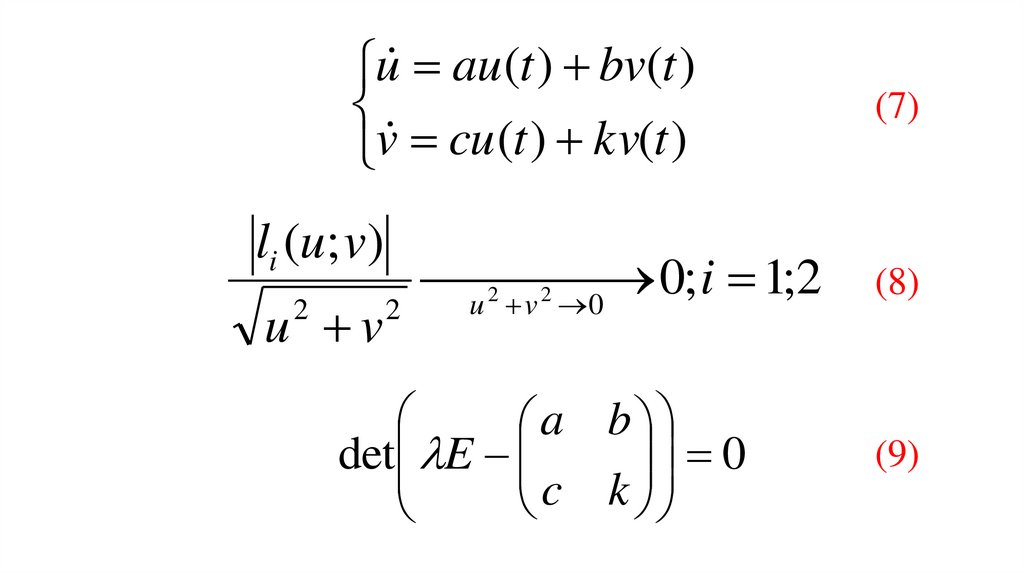






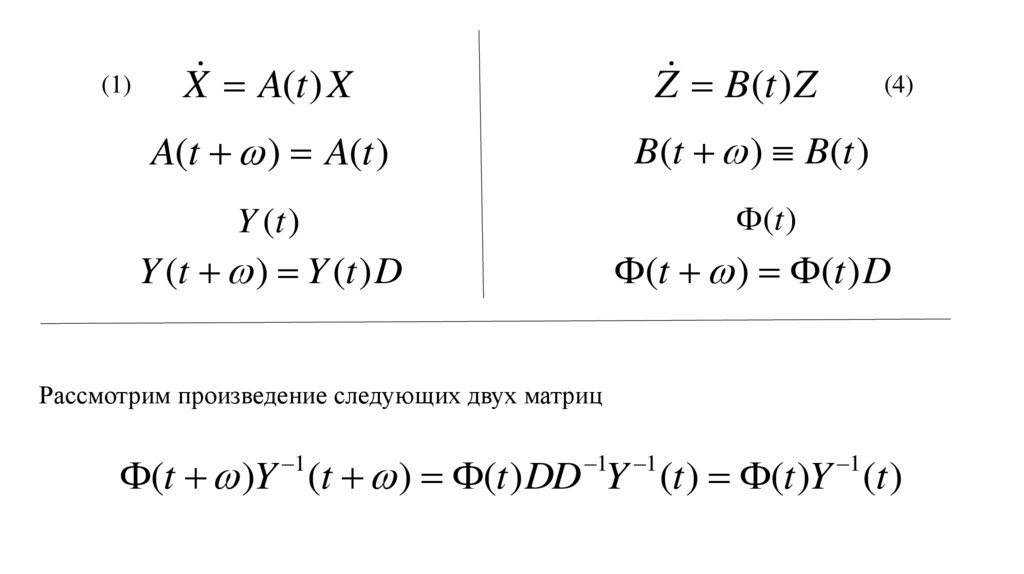







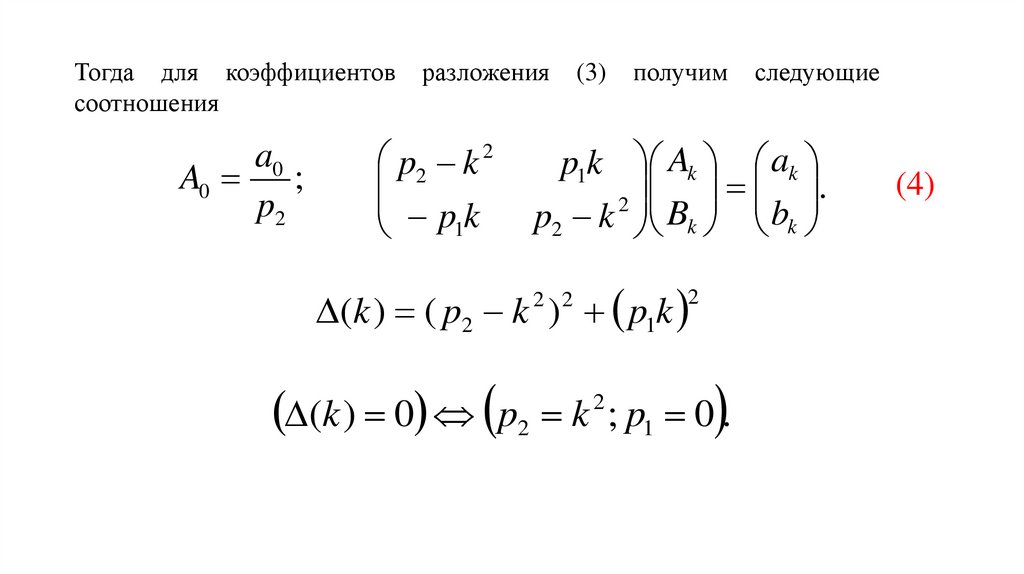

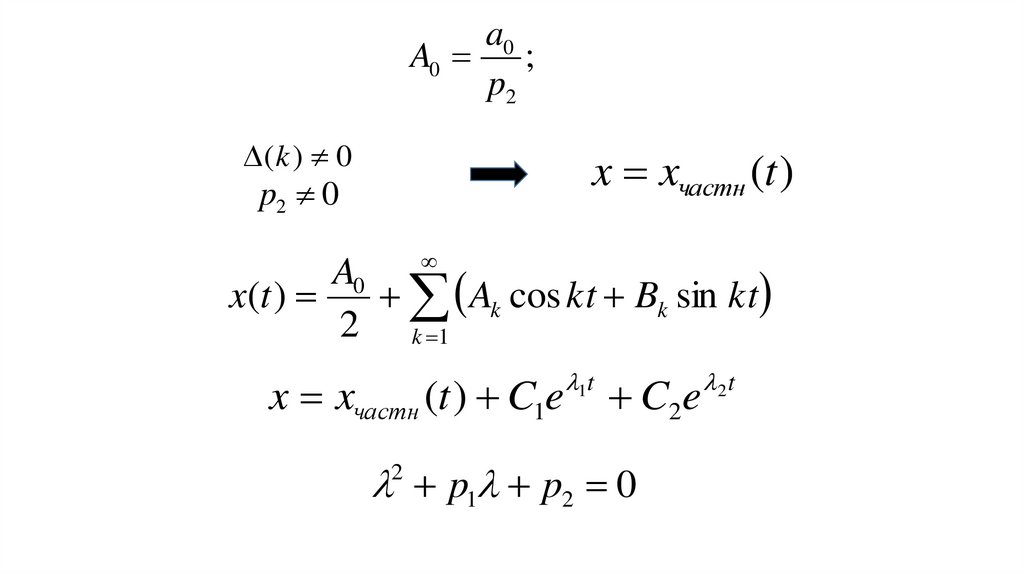
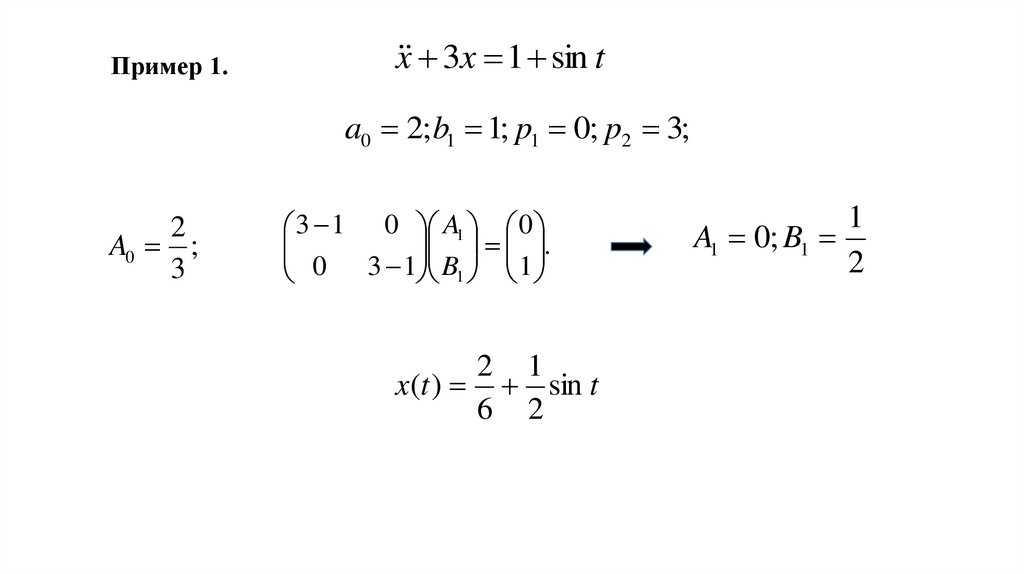
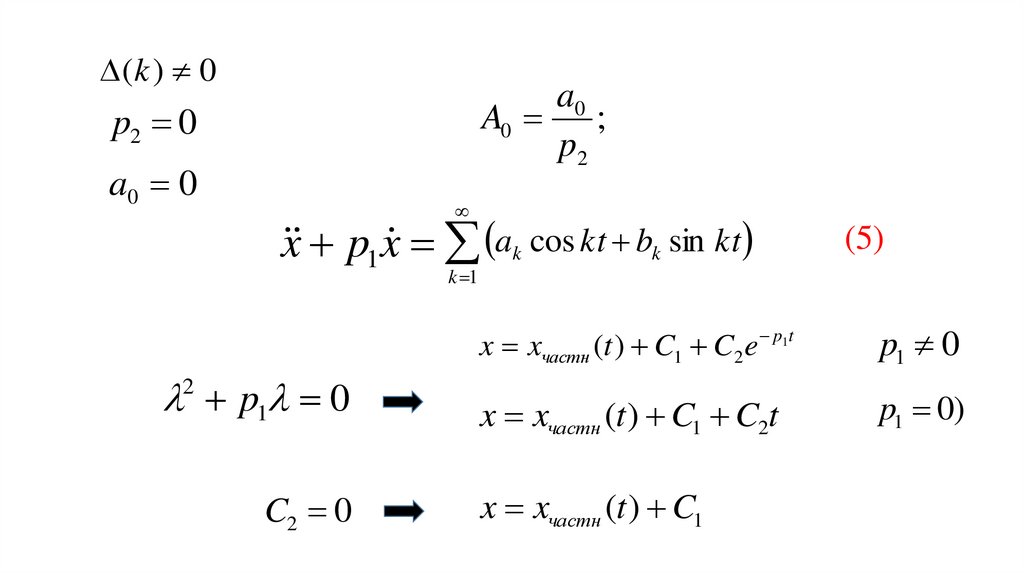
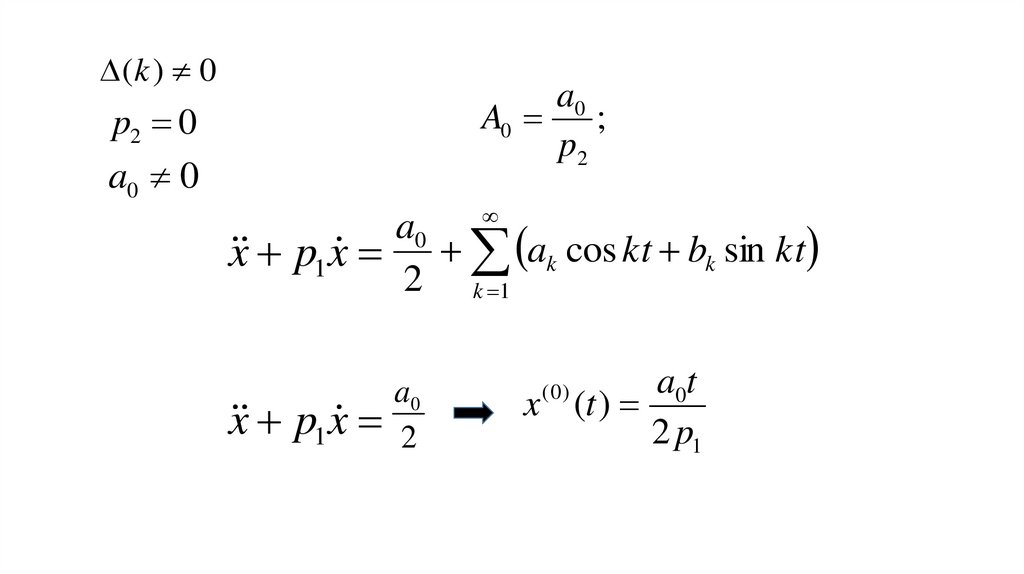



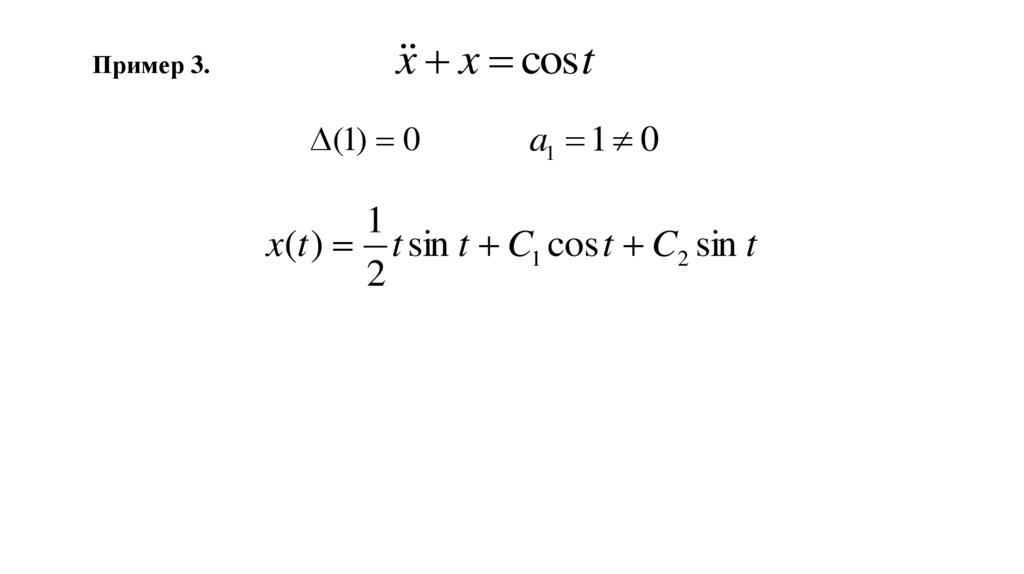
 Математика
Математика








