Похожие презентации:
Взаимное расположение графиков линейных функций
1. Взаимное расположение графиков линейных функций.
Муниципальное автономноеобщеобразовательное учреждение средней
общеобразовательной школы №1.
Взаимное расположение
графиков линейных функций.
.
алгебра, 7 класс
г.Березники
Юдина Л.В.
учитель
математики
2. Цели урока
Цели:• Рассмотреть разные случаи взаимного
расположения графиков линейных
функций.
• Научились распознавать взаимное
расположение графиков линейных
функций в зависимости от
коэффициента k.
3. Экспресс – опрос:
Какую функцию называют
линейной?
Линейной называют функцию вида
y =k x+в, где х- независимая
переменная, к и в- некоторые числа.
Что является графиком линейной
функции?
Графиком линейной функции
является прямая.
Какой формулой задаётся прямая
пропорциональность?
Прямой пропорциональностью
называется функция вида y=k x, где
х- независимая переменная, к- не
равное нулю число.
От чего зависит угол между прямой
и положительным направлением
оси ОХ?
Если k>0,то угол острый; если
k<0,то угол тупой.
Что является графиком уравнения
у =b?
у =b – прямая, параллельная оси
ОХ .
4.
НАЙДИ ОШИБКУ!• Ученик допустил ошибку при построении
графика одной из функций. На каком рисунке
ошибка?
у=2х+3
У
У
2
3
01
1
Х
У
у=0,5х
У=-х-3
-3
0
Х
1
2
Х
-3
01
-3
3
5. Исследование графиков линейных функций.
Заполните таблицы для построения графиков функций.1 вариант
2 вариант
2) у=2х
1) у=2х+4
1) У= - 2х+3
х
0
-2
х
0
2
х
у
4
0
у
0
4
у
3) у=2х-2
4) у=2х-4
0
1
3
1
3) У = - х + 3
х
0
2
х
0
2
у
-2
2
у
-4
0
х
у
0
3
2) У = 0,5х+3
х
-6
у
0
0
3
4) У = х + 3
х
3
0
у
-3
0
0
3
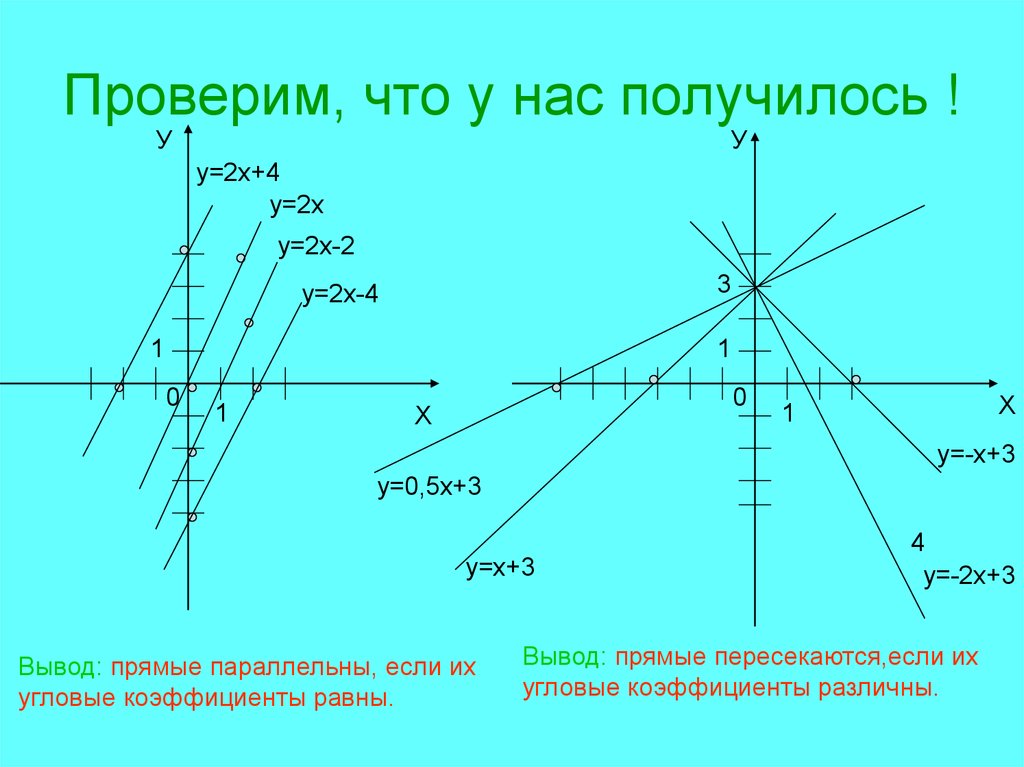
6. Проверим, что у нас получилось !
УУ
у=2х+4
у=2х
у=2х-2
3
у=2х-4
1
1
0
1
0
Х
Х
1
у=-х+3
у=0,5х+3
у=х+3
Вывод: прямые параллельны, если их
угловые коэффициенты равны.
4
у=-2х+3
Вывод: прямые пересекаются,если их
угловые коэффициенты различны.
7.
Ось абсцисс. Раз. Два. Подтянулись.Ось ординат. Подтянулись.
Прямая .y=kx+b.
K – положительное. Наклон вправо. Подтянулись.
K – отрицательно. Наклон влево. Подтянулись.
И еще раз.
Закроем глаза, проделаем круговые движения
глазами влево, вправо, откроем глаза и быстро
поморгаем.
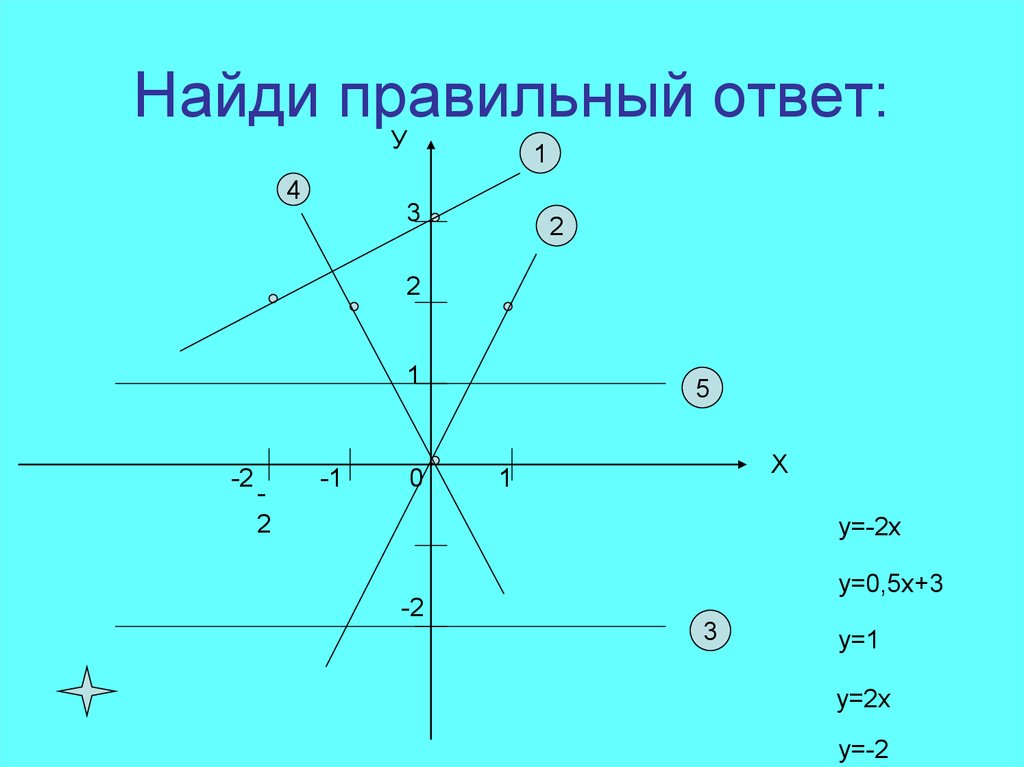
8. Найди правильный ответ:
У4
1
3
2
2
1
-2
2
-1
0
5
Х
1
у=-2х
у=0,5х+3
-2
3
у=1
у=2х
у=-2
9. Правильно!
Это прямые у =0,5х+3 и у = -2хА вот ещё несколько примеров :
10.
У3
у=0,2х+1
У
У=3x-1
5
1
Х
0
1
4
5
у=-1/3 х+3 3
У = - 5х+3
1
0
-3
-1
1
Х
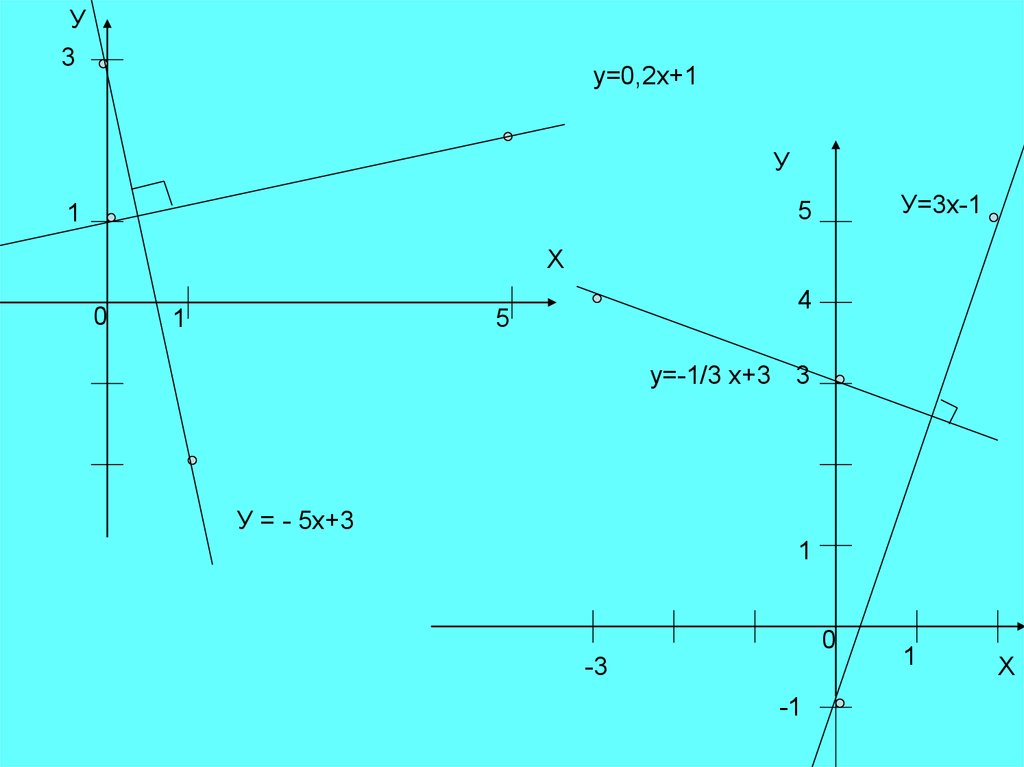
11. ВНИМАТЕЛЬНО ПОСМОТРИТЕ НА УРАВНЕНИЯ ПЕРПЕНДИКУЛЯРНЫХ ПРЯМЫХ И ПОПРОБУЙТЕ ОТВЕТИТЬ НА ВОПРОС:
При каком условии две прямые взаимноперпендикулярны ?
У = 0,5х+3
и
У = - 2х
У = - 5х+3
и
У = 0,2х+1
У =3х – 1
и
У =- 1/3 х+3
12.
Первая подсказка:Обратите внимание на угловые коэффициенты:
0,5 и - 2
- 5 и 0,2
3 и – 1/3
Вторая подсказка:
Умножьте угловые коэффициенты:
0,5 *(-2)= -1
- 5*0,2= -1
3* (-1/3)= -1
13. Так когда же две прямые перпендикулярны ?
Вывод : две прямыеперпендикулярны , если
произведение их угловых
коэффициентов равно – 1.
14. Давайте теперь оформим результаты всех наших исследований и уточним …
• За что же «отвечает» угловойкоэффициент k ?
• Как «влияет» на положение прямой
число в ?
15. Число k:
ЧислоЛинейные
функции :
У = k1 x +в1
У = k 2 x + в2
Условие :
k:
Вывод :
k1=k2
Прямые
параллельны.
k 1= k 2
Прямые
пересекаются.
k 1 * k 2= - 1
Прямые
перпендикуляр
ны.
16. Число в :
Число1
y=
в:
у
x + в1
У = к х +в2
k
У=кх
в2
0
в1
х
17. Самостоятельная работа .
Даны две линейных функции y=k1x+b1иy=
k2x+ b2
Подберите такие координаты k1, k2, числа b1, b2,
чтобы их графики были:
а) были параллельны;
б) пересекались;
в) пересекались под прямым углом
18.
Д/З.У=3х+3 и у=3(х+1)
1. №342, 340(б).
2. №342, 343, 380.
3. №342, 344(а), 382.














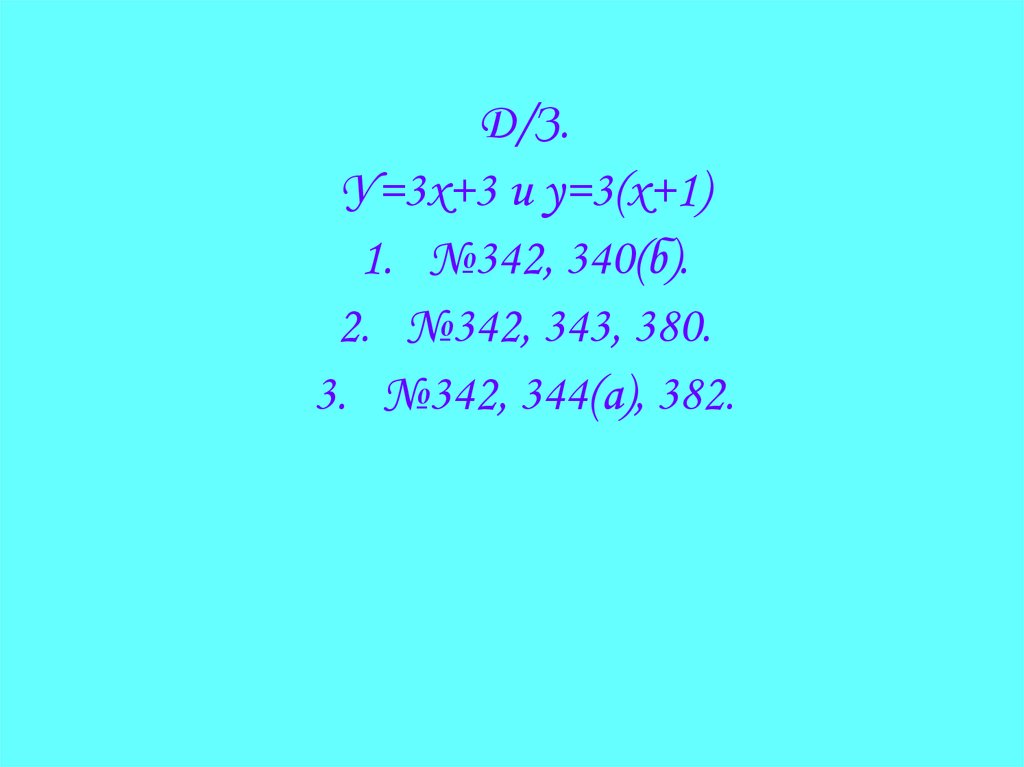
 Математика
Математика








