Похожие презентации:
Обыкновенные дроби. 5 класс
1.
Обобщающий урок поматематике по теме:
5 класс.
2.
•Повторить и закрепить изученные потеме правила.
•Закрепить полученные навыки
действий с обыкновенными дробями.
•Повторить методы решения задач по
данной теме.
•Познакомиться с некоторыми
историческими сведениями об
обыкновенных дробях.
3.
•Отработка правил по теме «Обыкновенныедроби».
•Устная работа.
•Тест по теме «Сложение и вычитание
обыкновенных дробей с одинаковыми
знаменателями».
•Выполнение упражнений по теме сложение
и вычитание обыкновенных дробей.
•Решение уравнений.
•Решение задач по данной теме.
4.
Повторим правила.•Дробь, в которой числитель меньше
знаменателя, называют правильной дробью.
•Дробь, в которой числитель больше
знаменателя, называют неправильной дробью.
•Из двух дробей с одинаковыми
знаменателями меньше та, у которой меньше
числитель, и больше та, у которой больше
числитель.
5.
Поставьте знак > или < в записях:3
13
1)
19 < 19
23
21
2)
>
100 100
87
<1
3)
97
117
4)
>1
82
Верно ли, что:
157
289
меньше
289
157
12 больше 140
140
11
6.
Повторим правила.•При сложении дробей с одинаковыми
знаменателями числители складывают, а
знаменатель оставляют тот же.
•При вычитании дробей с одинаковыми
знаменателями из числителя уменьшаемого
вычитают числитель вычитаемого, а
знаменатель оставляют тот же.
•При сложении ( вычитании ) чисел в
смешанной записи целые части складывают
( вычитают ) отдельно, дробные – отдельно.
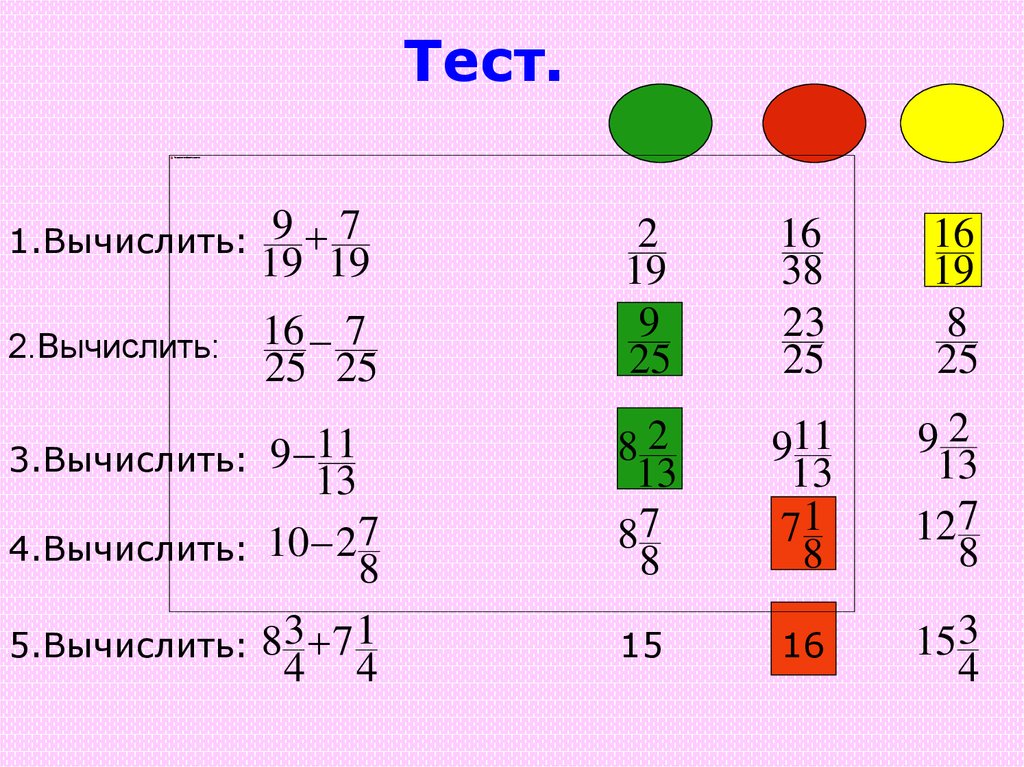
7.
Тест.1.Вычислить:
9 7
19 19
2.Вычислить:
16 7
25 25
3.Вычислить: 9 11
13
4.Вычислить: 10 2 7
8
5.Вычислить: 8 3 7 1
4 4
2
19
9
25
16
38
23
25
16
19
8
25
82
13
87
8
911
13
71
8
92
13
12 7
8
15
16
153
4
8.
Повторим правила.Чтобы из неправильной дроби
выделить целую часть, надо:
1)разделить с остатком числитель на
знаменатель;
2) неполное частное будет целой частью;
3) остаток (если он есть) дает числитель, а
делитель – знаменатель дробной части.
Выделите целую часть из дробей:
5
1 ; 18 2 4
1
7
4
4 7
;
83
8
3
25 25
;
503
3
5
100
100
77
1
;
77
9.
Повторим правила.Чтобы представить смешанное число
в виде неправильной дроби нужно:
1)умножить его целую часть на знаменатель дробной
части;
2) к полученному произведению прибавить числитель
дробной части;
3) записать полученную сумму числителем дроби, а
знаменатель дробной части оставить без
изменения.
Представьте в виде неправильной дроби:
1 49 ; 3 23 ; 3 1003
5 85
6
8
5
; 5
8 8
125 125
16 16
4 4
10.
Выполните вычисления:15
8 8
8
7
2. 12 35 4
9 9
9
4
7
3
3. =
10 10 10
1. 13 2 =
и
0
а
7.
7 1
8 8 1
3
н
5
54
5. 23 4 1
ы
5 5
52
6. 6 9 1 6 8
л
13 13 13
4. 23 2
м
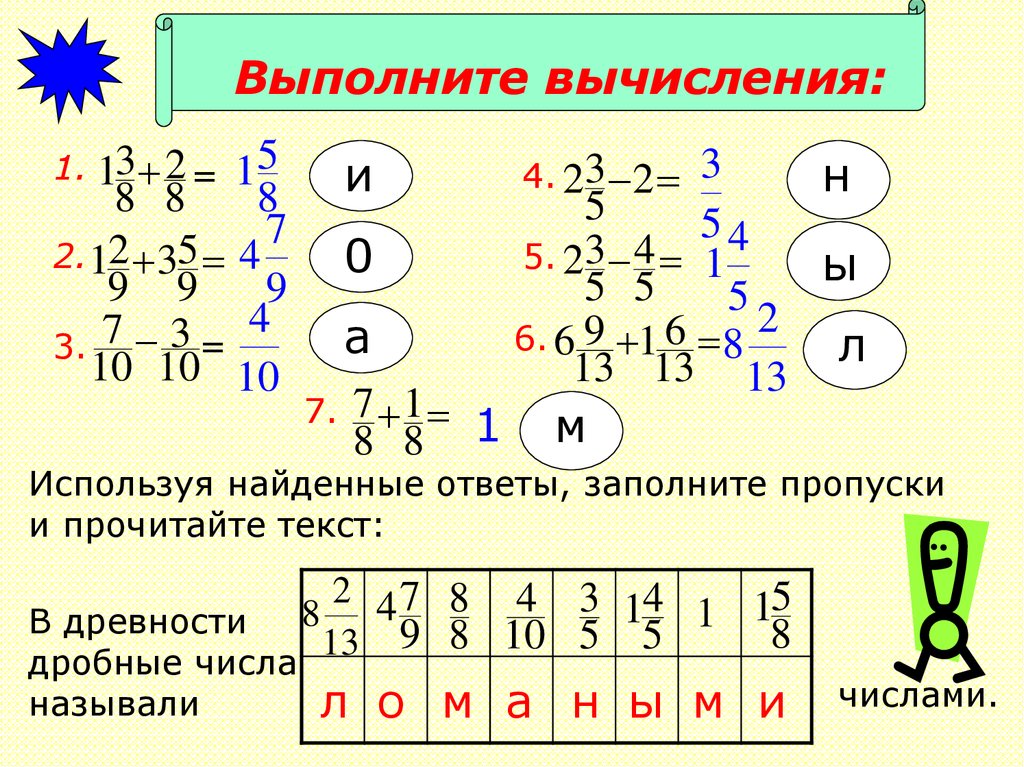
Используя найденные ответы, заполните пропуски
и прочитайте текст:
В древности
дробные числа
называли
2 47 8 4 3 4
1 1 15
8
8
13 9 8 10 5 5
л о м а н ы м и
числами.
11.
В Египте для записи некоторыхдробей использовали особые знаки.
Вычислите:
6 11 : 2 17 : 2 1 : 2 1
17
17
17
2
1 4 1 0 1 1
3 3
4 3
2 5 3 7 3
3 4 3 1
1
7 7 4 7 4
4 4 4 4
4
2 2
1
2
5 4 4 4
3
3
3
3 3
12.
Решите уравнения(самостоятельно)
I вариант
3
8
7 t 5
17
17
3
8
t 7 5
17 17
20
8
t 6 5
17 17
12
t 1
17
12
Ответ: t 1
17
II вариант
8
18
x 8 3
19 19
18
8
x 3 8
19 19
26
x 11
19
7
x 12
19
7
Ответ: x 12
19
13.
1711
Катя 1 часа готовила обед и
часа убирала
20
20
квартиру. Сколько времени потратила Катя на
домашнее хозяйство ? На сколько больше
времени Катя затратила на приготовление
обеда, чем на уборку квартиры ?
17
Обед- 1
часа
20
Всего ?
11
часа
20
На сколько больше времени затрачено
на обед, чем на уборку ?
Уборка квартиры-
14.
17Обед- 1
часа
20
Всего ?
11
часа
20
На сколько больше времени затрачено
на обед, чем на уборку ?
Уборка квартиры-
17 11 28
8
(час.)-всего затратила
1. 1 1 2
20 20 20
20
17 11
6
2. 1 1 (час.)
20 20 20
8
Ответ: 2
часа затратила Катя на обед и уборку.
20
6
На 1
часа затратила больше на обед.
20
15.
Муж и жена брали деньги из одного сундука, иничего не осталось. Муж взял 7 всех денег, а
10
жена 690 рублей. Сколько было всех денег?
7
Муж- всех денег
10
Жена-690 рублей.
Всего-?
1. 1 7 10 7 3
10 10 10 10
- такую
часть денег
взяла жена
2.690:3. 10=2300(руб.)
Ответ: всего было 2300 рублей.
16.
Кролик решил на огороде длиной 10 метров и шириной4 метра посадить капусту и морковь. Морковью он
засеял
площади этого огорода, а остальное капустой.
Какая часть огорода занята капустой? На сколько
квадратных метров площадь, занятая морковью,
больше чем площадь, занятая капустой?
Длина- 10 м
Ширина- 4 м
2 5
Морковь- ?м
S огорода.
2 8
Капуста- ?м остальная
часть огорода
На сколько S, занятая
морковью, больше чем S,
занятая капустой?
17.
Длина- 10 мШирина- 4 м
2 5
Морковь- ?м
S огорода.
2 8
Капуста- ?м остальная
часть огорода
На сколько S, занятая
морковью, больше чем S,
занятая капустой?
1. 4 10=40 (м 2)- площадь поля.
2
2. 40: 8 5=25(м )- площадь, занятая
морковью.
2
3. 40-25=15(м )-площадь, занятая
капустой.
2
4. 25-15=10(м )
Ответ:15 м2 занято капустой.
2
На 10м площадь занятая,
морковью, больше, чем
площадь, занятая капустой.
18.
Какую часть квадратного метрасоставляет:
1 2
0
2
м
а) 1 дм =
100
1
2
2
м
б) 1 см =
10.000
10 2
2
м
в) 10 дм =
100
100
2 1м
2
м
г) 100 см =
10.000
1м
1дм2
10дм2
19.
Повторение:Решите задачу:
В прямоугольном параллелепипеде высота
на 20 см меньше ширины, а длина в 4 раза
больше ширины. Вычислите объем этого
прямоугольного параллелепипеда, если
высота равна 3 дм.
Решение
Высота -3 дм, на 20 см бол.
Ширина - ?
Длина – в 4 раза бол.?
Найти V.
20см=2дм
1)3+2=5(дм) –ширина.
2) 5 · 4=20(дм) –длина.
3
3) 3 · 5 · 20=300(дм )
Ответ: V=300 дм 3
20.
Домашнее заданиеПункт 29 ( вопросы )
№ № 1112, 1114.
Дидактические
материалы стр.95
№223.


















 Математика
Математика








