Похожие презентации:
График функции
1. График функции
Математика – самый короткий путьк самостоятельному мышлению.
В.Каверин
к
ГРАФИК ФУНКЦИИ у
х
y
k
x
Урок – объяснение нового материала
Учитель: Буторова О.В.
2. ПЛАН УРОКА
Слуховая работаМатематический спринт
Изучение нового материала
Решение заданий на построение графика
функции
Самостоятельная работа
Историческая справка
Экран настроения. Подведение итогов урока
3. СЛУХОВАЯ РАБОТА
ГОВОРИ ХОРОШО!Пропорция
График функции
Значение функции
Значение аргумента
Ось абсцисс, ось ординат
Обратная пропорциональность
4. Прочитай и назови ответ
25 % от числа 56 равно…Сумма чисел 4,71 и 12,5 равна…
Произведение 0,34 и 20 равно….
Разность 5 и 2/7 равна…
Частное 17,5 и 5 равно…
10% от числа 2 равно…
5. Соедини правильно
Ось ОХ - этоЗначение у - это
Точка (0; 0) - это
Ось ОУ - это
Значение х - это
у = 2х – 5 - это
начало координат
ось ординат
ось абсцисс
линейная функция
функция
аргумент
6. ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ
Обратной пропорциональностьюназывается функция, которую
можно задавать формулой вида
к
у
х
где у – зависимая переменная
х – независимая переменная,
k – не равное нулю число.
7. ОБРАТИТЕ ВНИМАНИЕ
В формулек
у
х
независимая переменная х
находится в знаменателе дро
Делить на 0 нельзя!
Областью определения функции
является множество всех чисел,
отличных от нуля
8. Укажите какие из функций являются обратной пропорциональностью?
13а) у
х
б) у 2х
в)
х
у
5
1
у х
14
25
у
21х
2х
у
41
2
у
х
х 6
у
5
4
у
11х
8
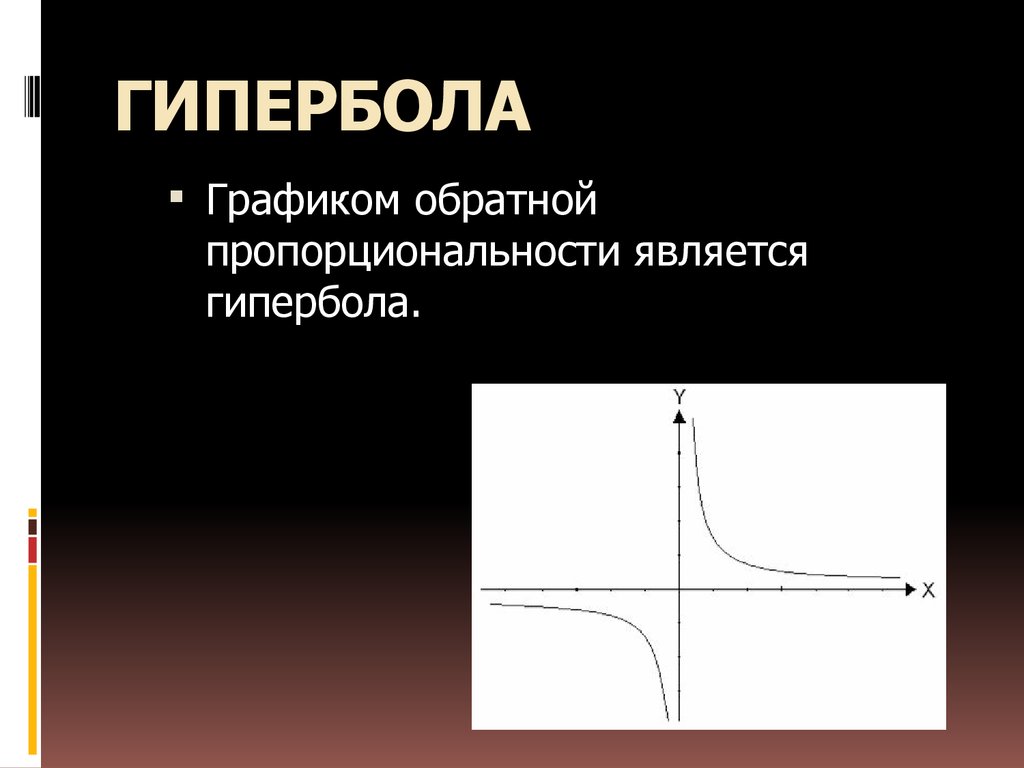
9. ГИПЕРБОЛА
Графиком обратнойпропорциональности является
гипербола.
10. Построить график функции у=12/х
1. обратная пропорциональность2. график – гипербола
3. область определения
4. таблица значений
11. Построить график у=-12/х
12. Самостоятельная работа
В одной и той же системе координатпостройте графики функций
ВАРИАНТ 1
у = 0,5х и
8
у
х
ВАРИАНТ 2
у = -2х – 4 и
6
у
х
Найдите точки пересечения графиков
функций.
13. ПРОВЕРИМ ОТВЕТЫ
ВАРИАНТ 1(-4; -2) И (4; 2)
ВАРИАНТ 2
(-3; 2) И (1; -6)
14. Гипербола (ὑπερβολή – греч.) - бросать далее цели, избыток.
ИСТОРИЧЕСКАЯ СПРАВКАГипербола (ὑπερβολή – греч.) бросать далее цели, избыток.
Открыта математиками
древнегреческой школы примерно в
IV в. до нашей эры
15.
Одним из первых, кто начал изучатьэту кривую был ученик знаменитого
Платона, древнегреческий математик
Менехм в IV в. до н.э., но так и не
сумел её полностью изучить. А вот
полностью исследовал свойства
гиперболы и дал ей название
крупнейший геометр древности
16. ПОДВЕДЕНИЕ ИТОГОВ УРОКА
Какую тему мы проходили?Что является графиком обратной
пропорциональности?
Что является графиком прямой
пропорциональности?
Кто такой Аполоний Пергский?









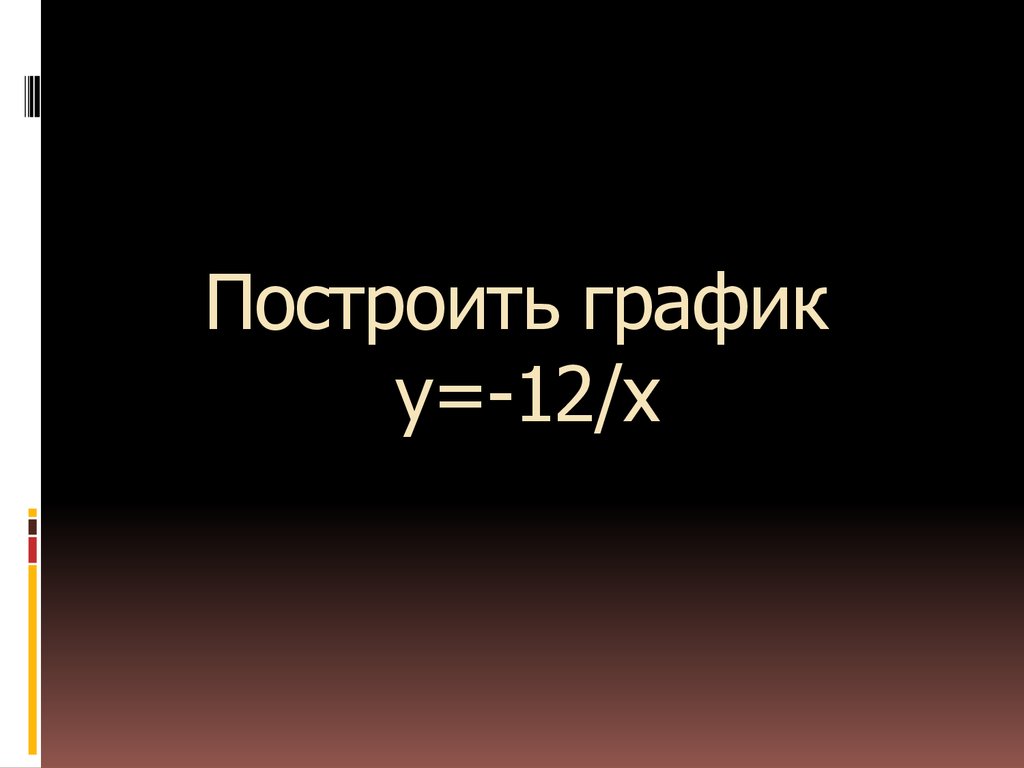






 Математика
Математика








