Взаимное расположение графиков линейной функции

1.

2.

Математический диктант
1.Определите значение коэффициентов k и b для каждой из функций
у = 2 – 4х
k = -4 ; b = 2
у = 2х
k=2;b=0
у = -3
k = 0 ; b = -3
2. Принадлежит ли точка А графику функции у = 3х – 5, если
А(2;1)
да
3. Решите уравнение:
5х + 2 = 3х
5х + 3 = 7 + 5х
-1
нет корней

3.

у
у = -2х - 2
у=х+7
А
4
1
-3
х ≈ -3 ; у ≈ 4
-1
0
Графики у = -2х -2 и у = х + 7
пересекаются в А (-3; 4)
х

4.

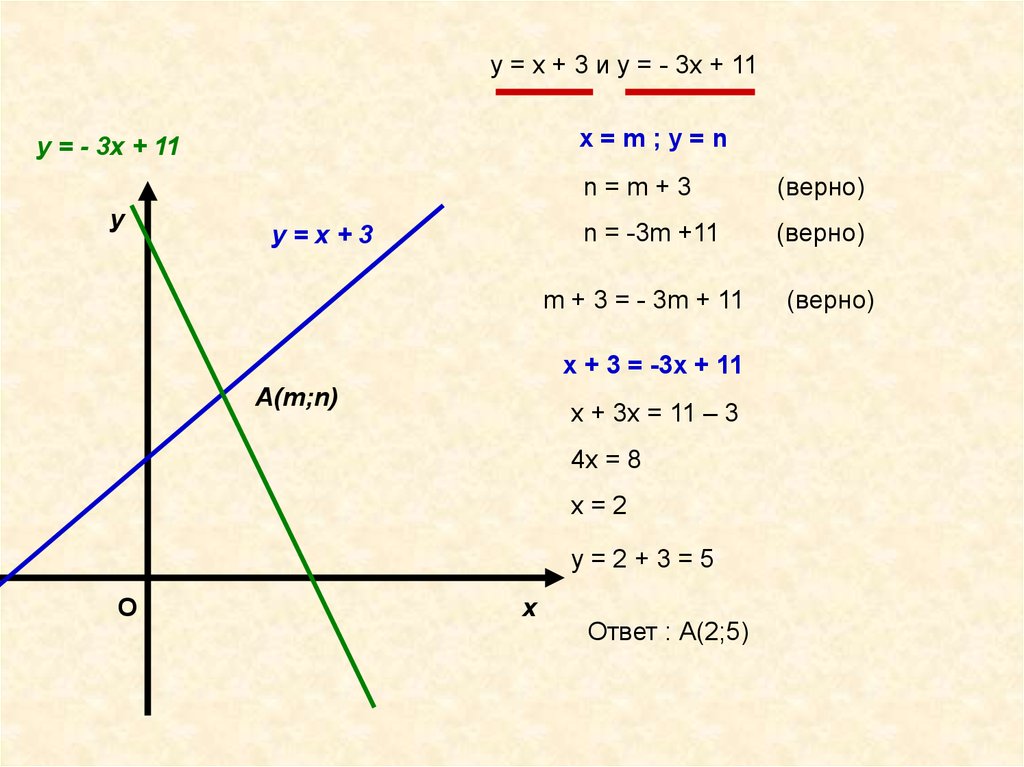
у = х + 3 и у = - 3х + 11
х=m;у=n
у = - 3х + 11
y
у=х+3
n=m+3
(верно)
n = -3m +11
(верно)
m + 3 = - 3m + 11
х + 3 = -3х + 11
А(m;n)
х + 3х = 11 – 3
4х = 8
х=2
у=2+3=5
О
x
Ответ : А(2;5)
(верно)

5.

у = k1x + b1 и
алгоритм
y = k2x + b2
пример
у = х + 3 и у = - 3х + 11
1. Находим абсциссу точки
пересечения графиков.(Составляем
уравнение, приравнивая правые
части) k1x + b1 = k2x + b2 .Решаем
уравнение.x = m
1. х + 3 = -3х +11
х + 3х = 11 – 3
4х = 8
х=2
2. Находим ординату точки
пересечения
у = k1m + b1 или y = k2m + b2
2. у = 2 + 3 = 5
у=5
3. Записываем ответ
(2;5) точка пересечения графиков
функций у = х + 3 и у = -3х + 11

6.

Найдите координаты точки пересечения графиков
функций у = 2х + 3 и у = 2х + 5
1. 2х + 3 = 2х + 5
2х – 2х = 5 - 3
0х = 2
корней нет

7.

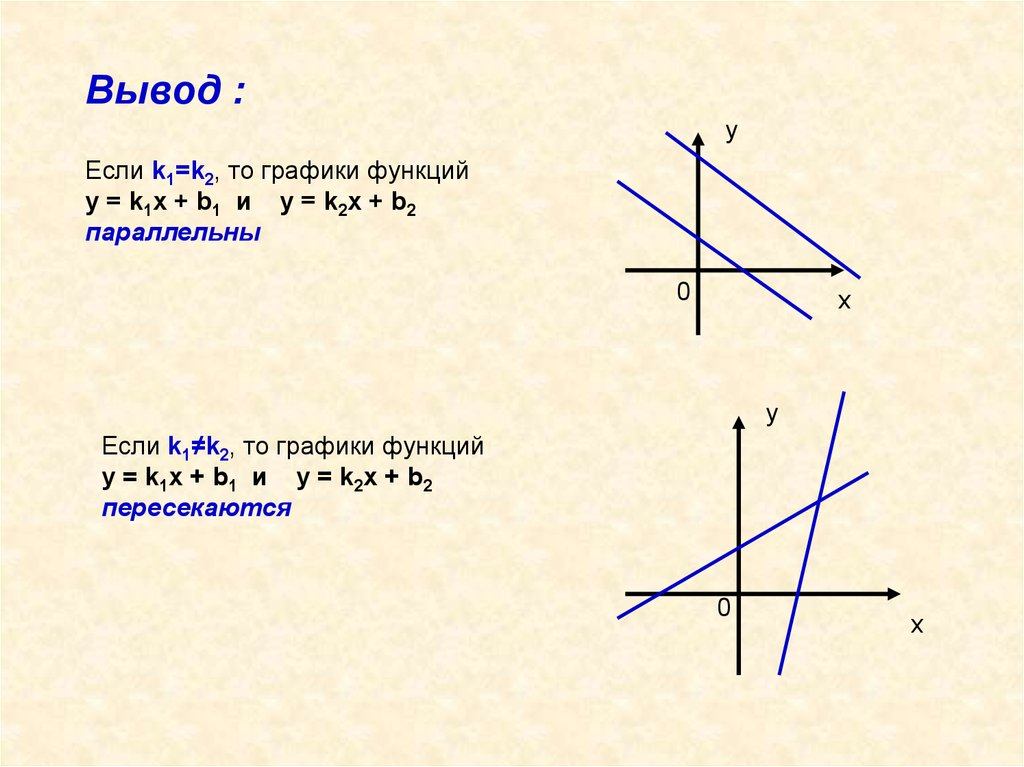
Вывод :
у
Если k1=k2, то графики функций
у = k1x + b1 и y = k2x + b2
параллельны
0
х
у
Если k1≠k2, то графики функций
у = k1x + b1 и y = k2x + b2
пересекаются
0
х

8.

у = 10х – 8 и у = -3х + 5
1) 10х – 8 = -3х + 5
10х+3х = 5 + 8
13х = 13
х=1
2) у = 10·1 – 8
у=2
Ответ : (1;2) точка пересечения графиков функций
у = 10х – 8 и у = -3х + 5