Похожие презентации:
Планиметрия: задачи, связанные с углами. Применение тригонометрии в геометрических задачах
1.
Применение тригонометрии в геометрическихзадачах
Планиметрия: задачи, связанные с углами
2.
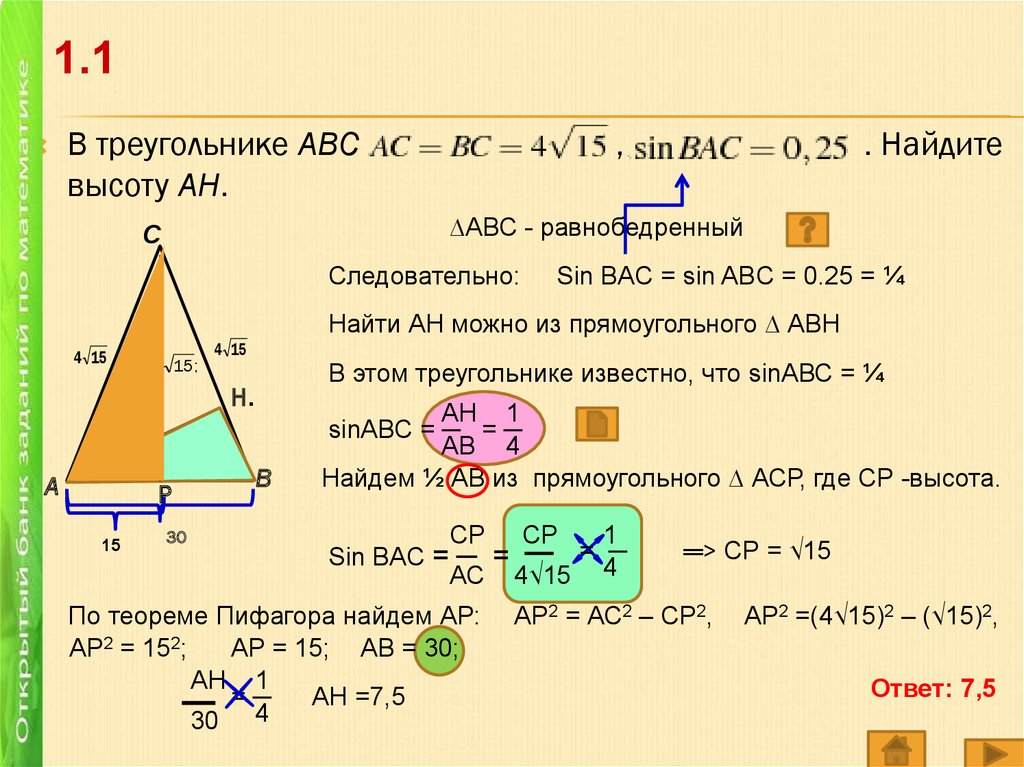
1.1В треугольнике ABC
высоту AH.
,
. Найдите
∆АВС - равнобедренный
С
Следовательно:
Sin BAC = sin ABC = 0.25 = ¼
Найти АН можно из прямоугольного ∆ АВН
4 15
15 ;
4 15
В этом треугольнике известно, что sinАВС = ¼
H.
A
B
Р
15
30
АН 1
sinАВС = ─ = ─
АВ 4
Найдем ½ АВ из прямоугольного ∆ АСР, где СР -высота.
СР
1
=
─
Sin BAC = ─ = ─
4
АС 4√15
По теореме Пифагора найдем АР:
АР2 = 152;
АР = 15; АВ = 30;
АН 1
=─
АН =7,5
4
30
─
СР
═> СР = √15
АР2 = АС2 – СР2,
АР2 =(4√15)2 – (√15)2,
Ответ: 7,5
3.
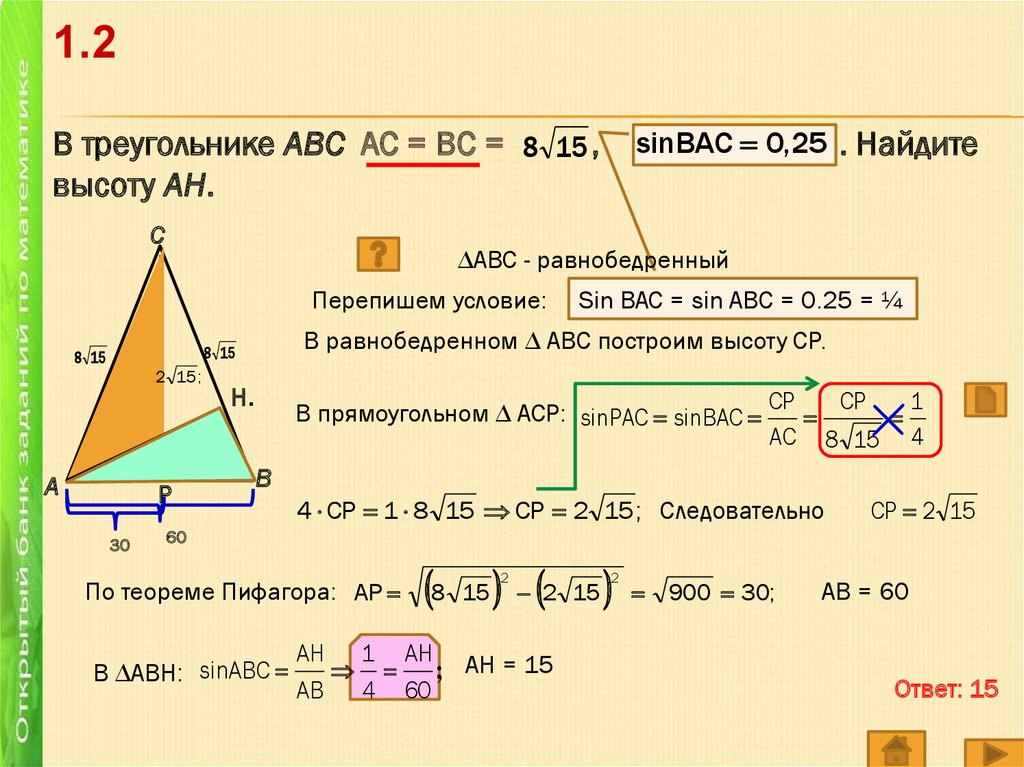
1.2sinBAC 0,25 . Найдите
В треугольнике ABC АС = ВС = 8 15 ,
высоту AH.
C
∆АВС - равнобедренный
Перепишем условие:
В равнобедренном ∆ АВС построим высоту СР.
8 15
8 15
2 15 ;
A
Р
30
Sin BAC = sin ABC = 0.25 = ¼
H.
В прямоугольном ∆ АСР: sinPAC sinBAC CP CP 1
AC 8 15 4
B
4 СР 1 8 15 СР 2 15 ; Следовательно
СР 2 15
60
По теореме Пифагора: АР
В ∆АВН: sinABC
8
15
2
2
AH 1 AH АН = 15
;
AB 4 60
15
2
900 30;
АВ = 60
Ответ: 15
4.
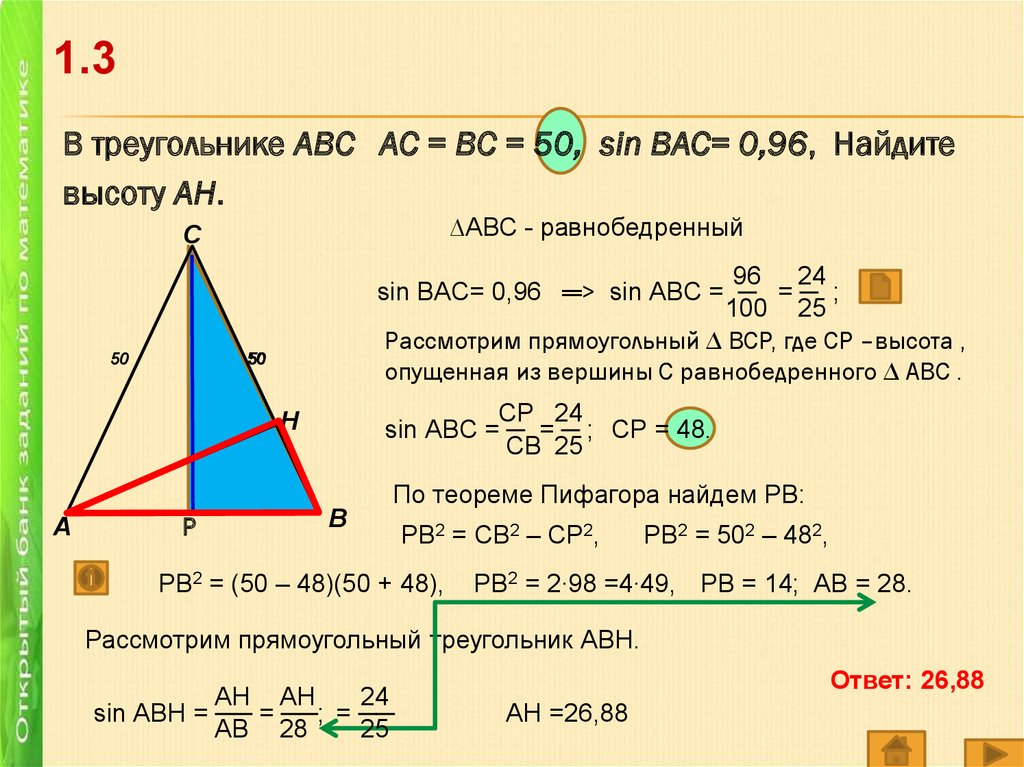
1.3В треугольнике ABC АС = ВС = 50, sin BAC= 0,96, Найдите
высоту AH.
∆АВС - равнобедренный
C
50
96 24
sin BAC= 0,96 ═> sin АBC = ─ = ─ ;
100 25
Рассмотрим прямоугольный ∆ ВСР, где СР –высота ,
опущенная из вершины С равнобедренного ∆ АВС .
50
СР 24
sin АBC = ─ = ─ ; СР = 48.
СВ 25
Н
По теореме Пифагора найдем РВ:
A
Р
B
РВ2 = СВ2 – СР2,
РВ2 = (50 – 48)(50 + 48),
РВ2 = 502 – 482,
РВ2 = 2∙98 =4∙49, РВ = 14; АВ = 28.
Рассмотрим прямоугольный треугольник АВН.
АН АН
24
sin АBН = ── = ──; = ──
АВ 28
25
Ответ: 26,88
АН =26,88
5.
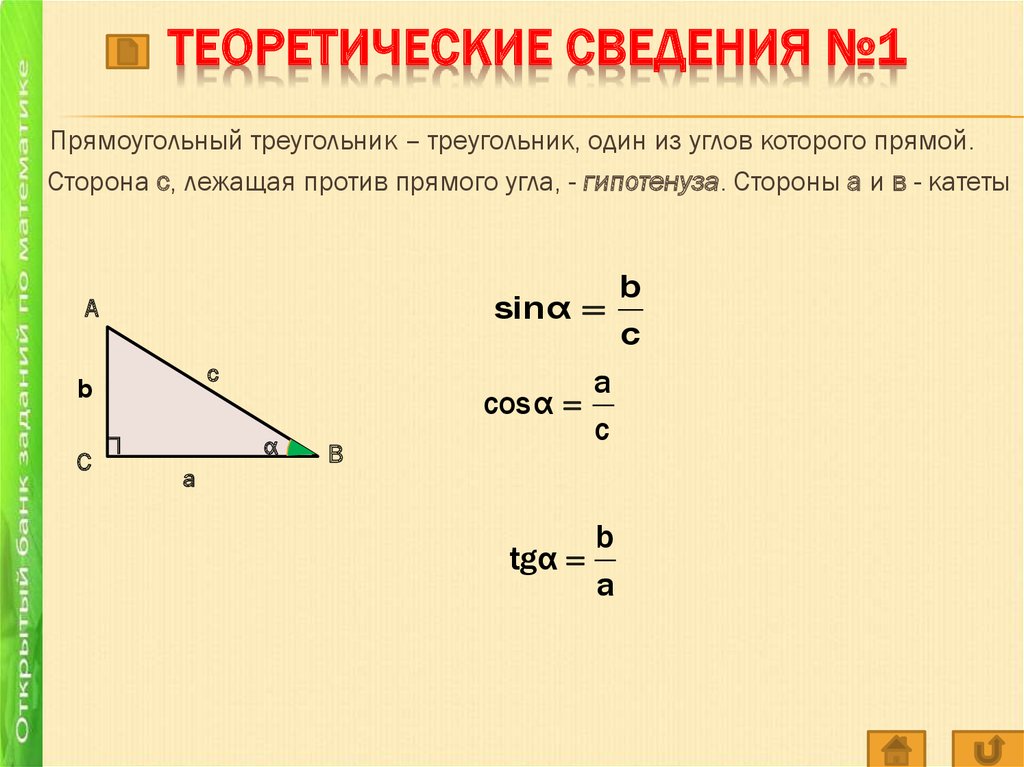
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №1Прямоугольный треугольник – треугольник, один из углов которого прямой.
Сторона с, лежащая против прямого угла, - гипотенуза. Стороны а и в - катеты
А
с
b
C
┐
α
а
В
b
sinα
c
а
соsα
с
b
tgα
a
6.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №21. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике высота, проведенная к основанию,
является и медианой, и биссектрисой.
СР – высота, медиана, биссектриса.
С
Медиана треугольника, проведенная из данной вершины, - отрезок
прямой, соединяющий эту вершину с серединой противолежащей
стороны треугольника
Высота СР разделила ∆ АВС на два равных
прямоугольных треугольника
А
Р
В
7.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ №3Основное тригонометрическое тождество
1.
sin 2 cos 2 1
cos 2 1 sin 2
cos 2 1 sin 2
2.
1
1 tg
cos 2
1
1 ctg 2
sin 2
2
Формулы сокращенного умножения:
а 2 в 2 (а в )(а в )
8.
СКОРО ЕГЭ!Еще есть время подготовиться!




 Математика
Математика








