Похожие презентации:
Модуль (абсолютная величина)
1. Модуль(абсолютная величина)
Выполнили: учитель МОУ СОШ №2Собенина Л.А.
2. Цели:
Образовательная: Повторить понятие модуля, свойствамодуля и решение простейших уравнений и
неравенств, содержащих модуль.
Развивающая: Развить внимание, память, логическое
мышление, пространственное воображение,
математически правильную речь.
Воспитательная: Воспитание аккуратности,
трудолюбия, ответственности за правильно
выполненную работу.
3. Определение модуля
a, еслиа 0,a
a, еслиа 0, а R
Определение
Аналогично для функции имеем:
f ( x), еслиf ( x) 0,
f ( x)
f ( x), еслиf ( x) 0.
Графически (геометрически) модуль числа а есть расстояние на
координатной прямой от точки а до начала отсчета.
a
d
4. Свойства:
1.a 0
2.
a a
a b a b
6.
a b a b
7.
3.
4.
5.
a a a2
2
2
ab a b
a a
,b 0
b b
Внимание
a a
2
f ( x) f ( x)
2
5. Уравнения, содержащие знак модуля
1.f ( x) b
f ( x) b, b 0
f ( x) b.
f ( x) b, b 0 решенийнет
f ( x) 0 f ( x) 0
g ( x) 0
2. f ( x) g ( x)
f ( x) g ( x)
f ( x) g ( x)
3.
f ( x) g ( x)
f ( x) g ( x)
f 2 ( x) g 2 ( x)
f ( x) g ( x)
6. Уравнения, содержащие знак модуля
4. В остальных случаях основным методом решения таких уравненийявляется метод интервалов:
1) Определяем ОДЗ уравнения.
2) Находим нули функции подмодульных выражений и разбиваем ими
ОДЗ уравнения на интервалы.
3) Решаем уравнение на любом из этих интервалов, предварительно
раскрыв модуль.
4) Решением уравнения является объединение всех найденных
решений.
7. Решить уравнения (устно)
1) x 7;6)2 3 x 1;
2) x 2;
7) x 3 x 3;
3) x 5 0;
4) x 1 3;
5) 9 x 4;
8)
4x
0;
3
9) 5 x x 5;
1
10) x x .
x
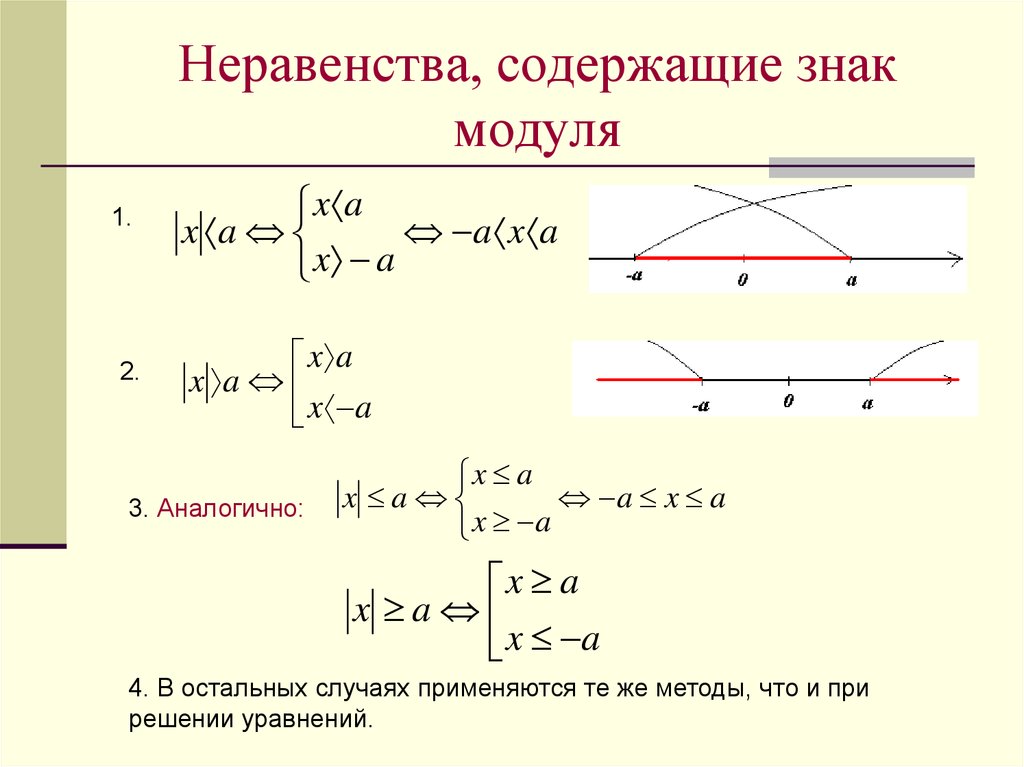
8. Неравенства, содержащие знак модуля
1.2.
x a
x a
a x a
x a
x a
x a
x a
3. Аналогично:
x a
x a
a x a
x a
x a
x a
x a
4. В остальных случаях применяются те же методы, что и при
решении уравнений.
9. Решите неравенства (устно)
1) x 1;6) x 1 1;
2) x 0;
7) 2 x 1 1;
3) x 0;
8) 2 x 1 3;
4) x 0;
9) x x 1 0;
5) x x;
10) x x 1 0.
10. Проверочная работа
1. Решите уравнение:2. Решите неравенство:
а ) х 2 3 х х 3 0;
а ) 1 2 х 0;
б ) 3х 5 5 2 х ;
б ) х 2 2 х 3 4;
в ) х 1 х 3 2;
в ) х 2 2 х х;
г ) х 1 х 1 2 0;
2
3
д)
х 3;
х 3 1
г ) х 1 х;
д) х 3 х 1 3;
е) х 1 3 х 2 х 4.
Внимание. При решении уравнений, в которых под знаком модуля
находится выражение, также содержащее модуль, следует сначала
освободиться от внутреннего модуля, а затем в полученных
уравнениях раскрыть оставшиеся модули.
х 4 х 2х 4









 Математика
Математика








