Похожие презентации:
Оптимизация химикотехнологичеких процессов. Безусловная оптимизация методом классического математического анализа
1.
1ОПТИМИЗАЦИЯ
ХИМИКОТЕХНОЛОГИЧЕКИХ
ПРОЦЕССОВ
Модуль 1. Лекция.
Безусловная оптимизация методом классического
математического анализа
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
2.
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИХТП
2
Оптимизация ХТП – это достижение наилучших результатов
функционирования ХТП (Химико-Технологического
Процесса)в смысле заданного критерия оптимальности
(целевой функции) при заданных условиях.
Корректное решение задачи оптимизации ХТП возможна
при выполнении следующих условий:
• выбран или сформулирован критерий оптимальности, представляющий
собой количественную оценку качества функционирования ХТП
• используемый при решении задачи оптимизации функционирующий
критерий оптимальности является единственным и количественным
• имеются в распоряжении ресурсы оптимизации – оптимизирующие или
управляющие параметры процесса (ХТП)
• функционирующий критерий оптимальности является чувствительным к
изменению оптимизирующих параметров ХТП
• разработана и реализована на компьютере адекватная модель процесса
• выбран и реализован на компьютере алгоритм оптимизации ХТП
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
3.
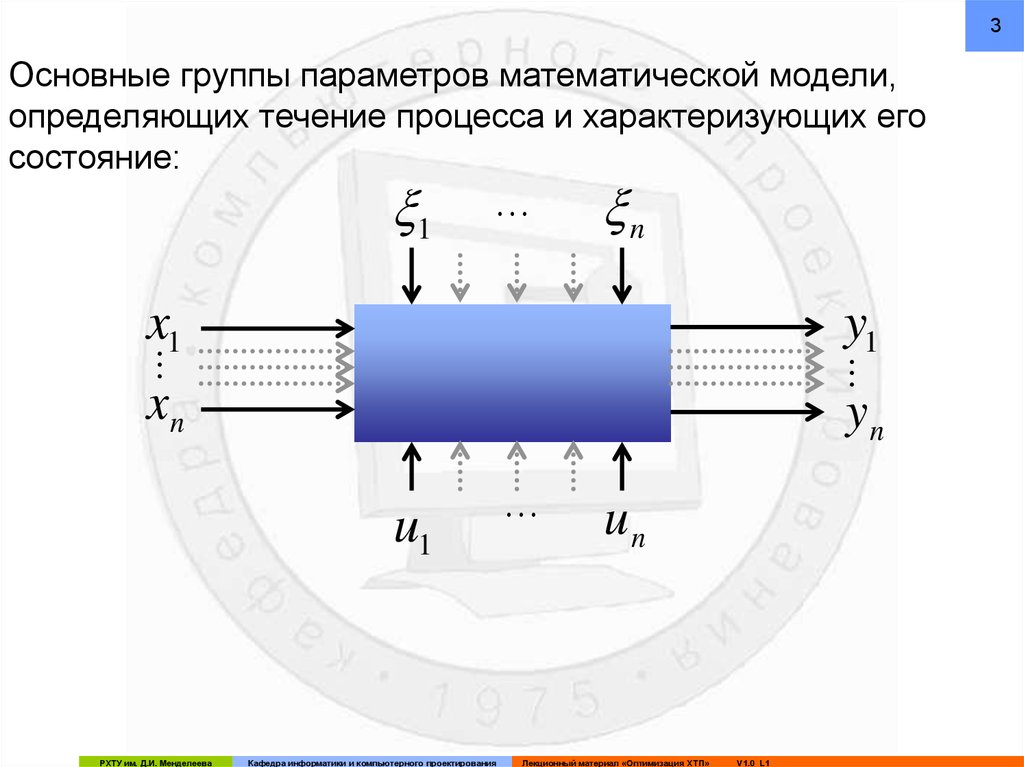
3Основные группы параметров математической модели,
определяющих течение процесса и характеризующих его
состояние:
1
n
x1
y1
xn
yn
u1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
un
Лекционный материал «Оптимизация ХТП»
V1.0 L1
4.
xu
y
- Входные параметры (влияющие на состояние
процесса, но на которые нельзя воздействовать)
- Управляющие(оптимизирующие) параметры –
ресурсы оптимизации (влияющие на состояние
процесса, на них можно воздействовать)
- Возмущающие параметры (не учитываются в
случае детерминированных процессов)
- Выходные параметры (характеризуют состояние
процесса).
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
5.
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИХТП
Математическая модель детерминированного процесса,
которая может быть реализована на компьютере
с применением alg ММ:
y (x, u )
Критерий оптимальности детерминированного процесса:
R R( x , y , u )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
5
6.
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП6
Решение задачи оптимизации – определение наименьшего (в
частном случае, min )или наибольшего (в частном случае,
max) величины R с применением alg ОПТ.
Поскольку выходные параметры y зависят от параметров
u , критерий оптимальности R при решении
x и
задачи оптимизации считается функцией только входных и
управляющих параметров процесса:
R R( x , u )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
7.
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТПТаким образом, задача оптимизации может быть решена с
применением компьютера только тогда, когда известен вид
зависимостей:
yi i ( x , u ) i 1, 2, ..., n
или адекватная математическая модель, позволяющая при
различных входных и управляющих параметрах процесса
определять его выходные параметры.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
7
8.
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП8
x
Однако так как на входные параметры
нельзя воздействовать,
они не могут быть оптимизирующими или управляющими параметрами.
Задача оптимизации решается с целью определения оптимальных
значений оптимизирующих или управляющих параметров u опт ,
при которых критерий оптимальности (целевая функция) R
принимает наибольшее (в частном случае – максимальное) или
наименьшее (в частном случае – минимальное) значение.
Корректное решение задачи оптимизации возможно только в диапазоне
входных x , управляющих
и выходных
параметров, в которых обеспечивается адекватность модели процесса.
u
y
В этом случае задача формулируется как задача на поиск экстремума
функции многих переменных
R R(u )
в области допустимых значений оптимизирующих (управляющих)
параметров
.
u
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
9.
9ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП
Если в дальнейшем принять, что u x , то
формулировка задачи оптимизации имеет вид и, в общем
случае, является задачей на экстремум функции многих
переменных (экстремальной задачей):
extr
R
(x
)
доп
x x
Таким образом, для решения задачи оптимизации требуется
определить такие значения оптимизирующих или
опт
управляющих параметров x
из области их допустимых
доп
значений x , при которых R принимает максимальное или
минимальное значение.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
10.
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП10
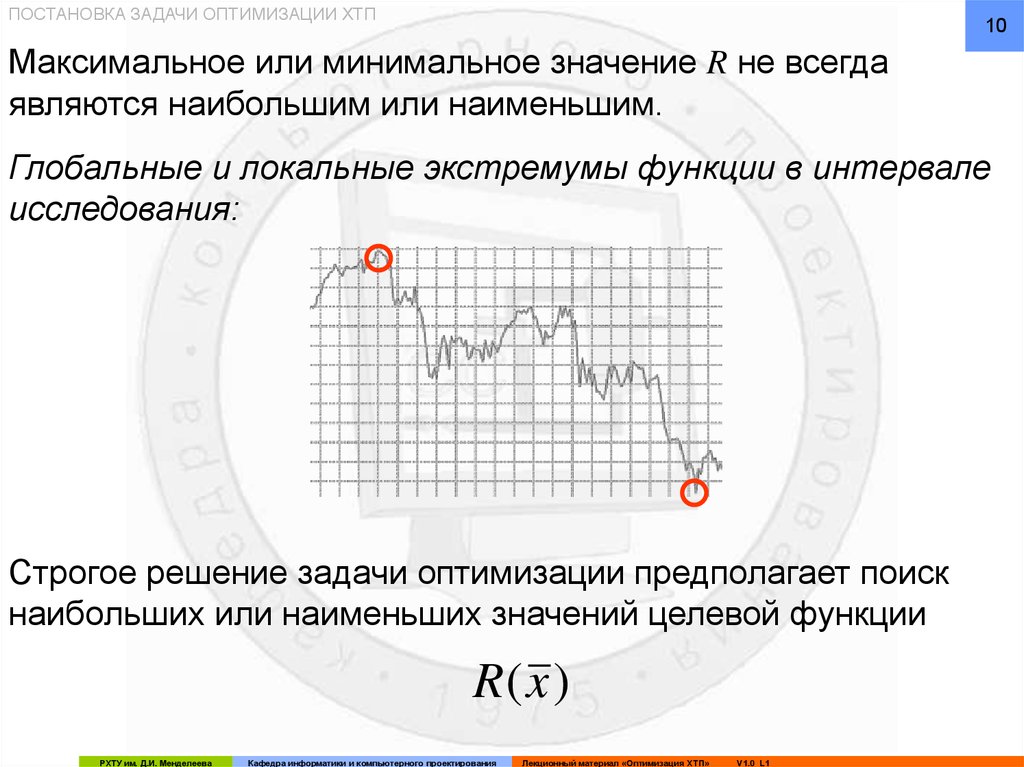
Максимальное или минимальное значение R не всегда
являются наибольшим или наименьшим.
Глобальные и локальные экстремумы функции в интервале
исследования:
Строгое решение задачи оптимизации предполагает поиск
наибольших или наименьших значений целевой функции
R (x )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
11.
ИССЛЕДОВАНИЕ ЭКСТРЕМУМАФУНКЦИЙ МЕТОДОМ КЛАССИЧЕСКОГО
МАТЕМАТИЧЕСКОГО АНАЛИЗА
11
Методы исследования функций классического анализа могут
применяться в случае, если известен вид зависимости
R (x )
При этом возможно аналитическое определение производных
оптимизируемой функции R, используемых для
формирования необходимых и достаточных условий
существования экстремума.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
12.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙПЕРЕМЕННОЙ
12
Необходимое условие существования экстремума
Непрерывная функция R(x) может иметь экстремумы при
таких значениях x, что:
R (x )
dR
a)
0
dx x xopt
max
min
( xopt x1 ) или ( xopt x2 )
x1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x2
V1.0 L1
x
13.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙdR
б)
dx
R (x )
max
13
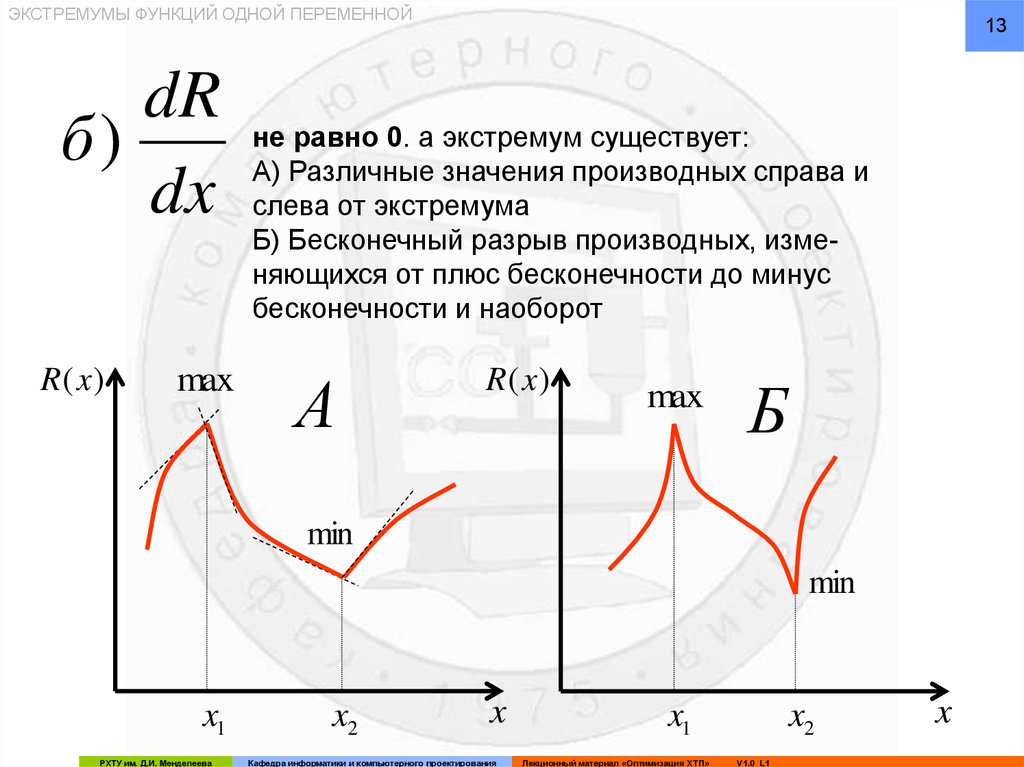
не равно 0. а экстремум существует:
А) Различные значения производных справа и
слева от экстремума
Б) Бесконечный разрыв производных, изменяющихся от плюс бесконечности до минус
бесконечности и наоборот
А
R (x )
max
Б
min
min
x1
РХТУ им. Д.И. Менделеева
x2
x
Кафедра информатики и компьютерного проектирования
x1
Лекционный материал «Оптимизация ХТП»
x2
V1.0 L1
x
14.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ14
R (x )
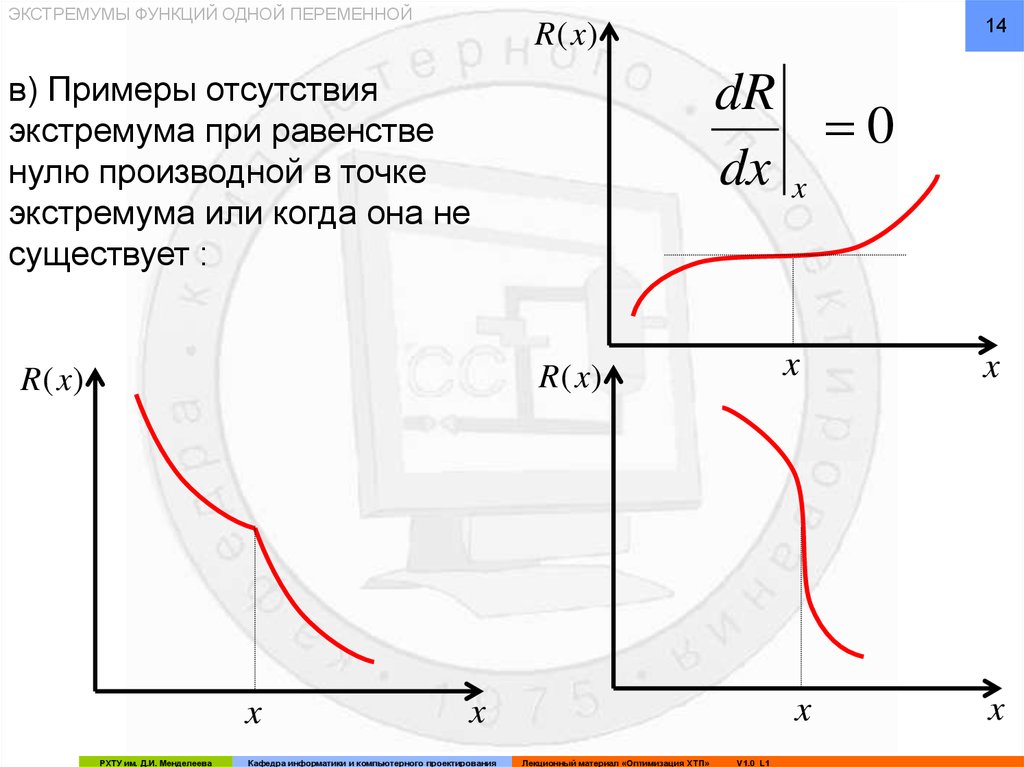
в) Примеры отсутствия
экстремума при равенстве
нулю производной в точке
экстремума или когда она не
существует :
dR
0
dx x
x
R (x )
R (x )
x
РХТУ им. Д.И. Менделеева
x
x
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
x
x
15.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ15
Для подтверждения наличия экстремумов в определенных
точках необходимо проводить дополнительные исследования:
1. Сравнение значений функции справа и слева от
предполагаемого экстремума
2. Сравнение знаков производных функции справа и слева от
предполагаемого экстремума
3. Исследование знаков производных высших порядков
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
16.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ16
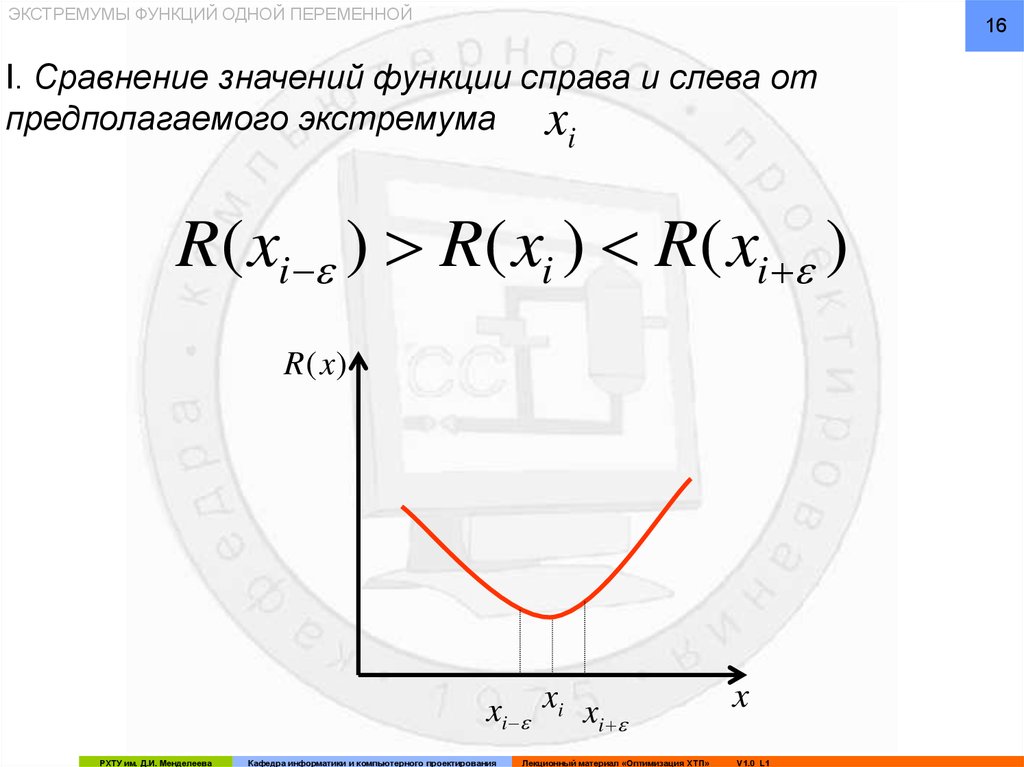
I. Сравнение значений функции справа и слева от
предполагаемого экстремума x
i
R( xi ) R( xi ) R( xi )
R (x )
xi xi xi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x
V1.0 L1
17.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ17
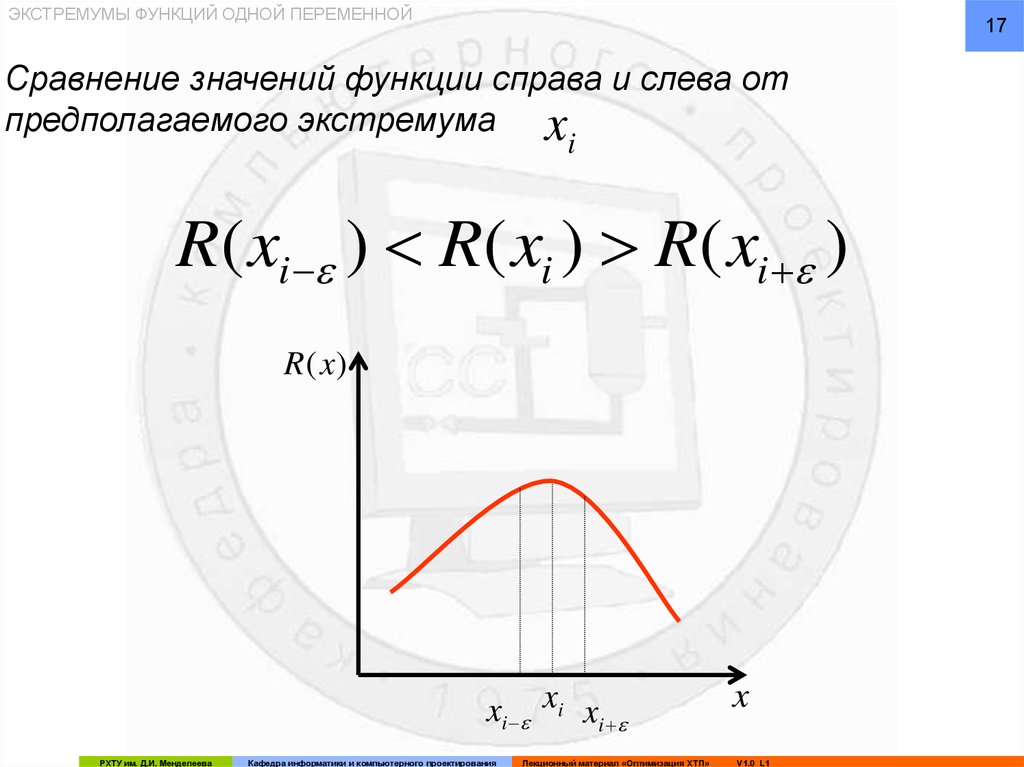
Сравнение значений функции справа и слева от
предполагаемого экстремума x
i
R( xi ) R( xi ) R( xi )
R (x )
xi xi xi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x
V1.0 L1
18.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ18
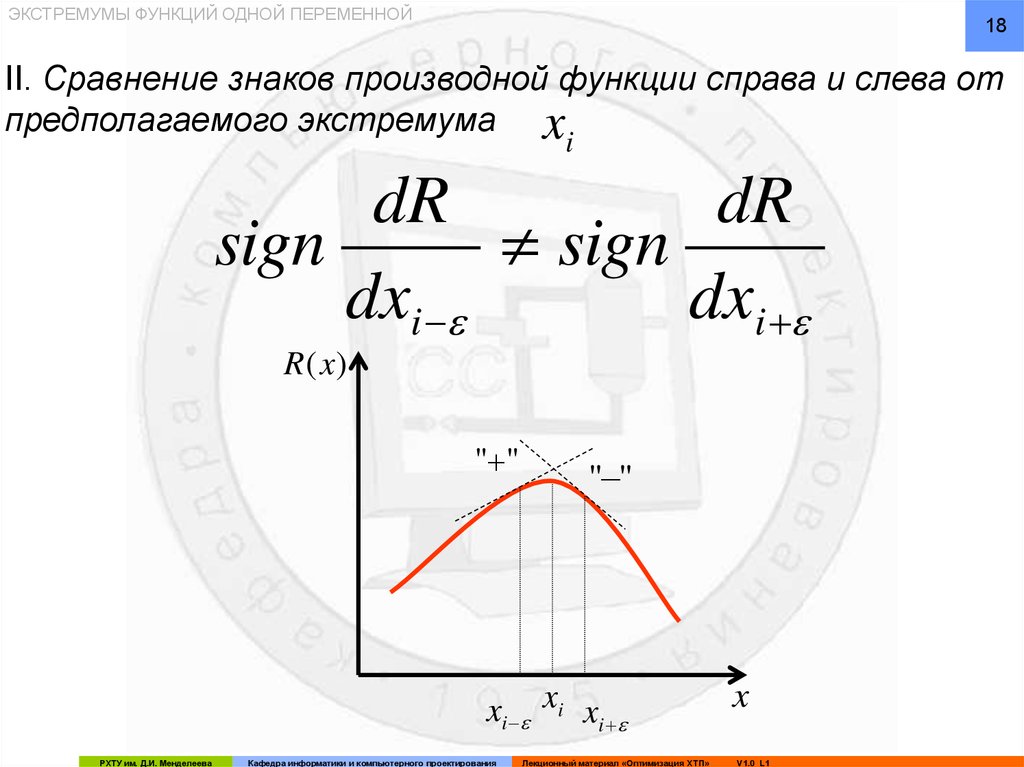
II. Сравнение знаков производной функции справа и слева от
предполагаемого экстремума x
i
dR
dR
sign
sign
dxi
dxi
R (x )
" "
" "
xi xi xi
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x
V1.0 L1
19.
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ19
III. Исследование знаков производных функции высших
порядков в точке предполагаемого экстремума x
opt
dR
0
dx xopt
2
d R
2
dx
0 max
xopt
R (x )
xopt
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x
V1.0 L1
20.
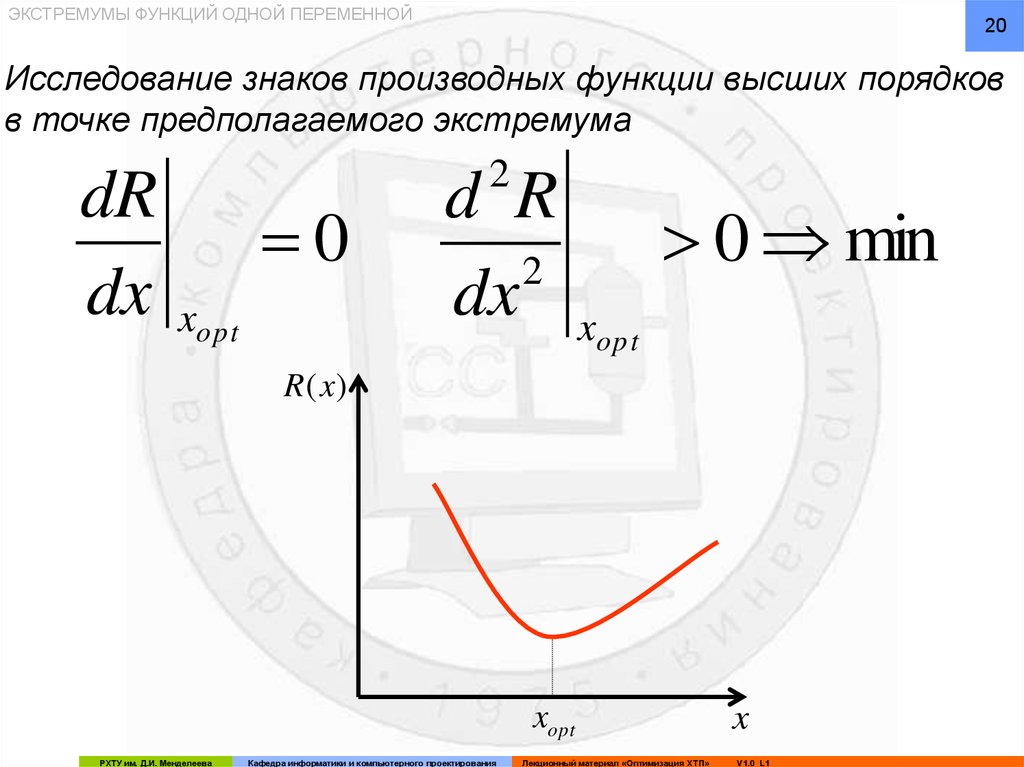
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ20
Исследование знаков производных функции высших порядков
в точке предполагаемого экстремума
dR
0
dx xopt
2
d R
0
min
2
dx x
opt
R (x )
xopt
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x
V1.0 L1
21.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХПЕРЕМЕННЫХ
21
xopt
Функция многих переменных R (x ) имеет в точке x
максимум (минимум), если существует такая окрестность этой
точки, взятая на области определения функции, что для всех
точек этой окрестности справедливо следующее неравенство:
( 0)
R( x ) R( x )
( 0)
или
R( x ) R( x )
( 0)
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
22.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ22
Необходимым условием существования экстремума
(0)
функции многих переменных в точке x является равенство
нулю частных производных первого порядка по всем
переменным:
R
0
x
i x x (0)
i 1, 2, ..., n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
23.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ23
Равнозначным условием является условие равенства нулю
полного дифференциала дифференцируемой функции R (x )
(0)
в точке экстремума x
Поскольку
dR( x ) x x ( 0 )
R
xn
dR( x ) x x ( 0 ) 0
R
x1
R
dx1
x2
x x (0)
R
dxn
x
(0)
i
1
i
x x
РХТУ им. Д.И. Менделеева
n
Кафедра информатики и компьютерного проектирования
dx2
x x (0)
n
dxi 0 dxi 0
x x (0)
Лекционный материал «Оптимизация ХТП»
i 1
V1.0 L1
24.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ24
Достаточные условия существования экстремума функции
многих переменных
Разложив функцию R (x ) в окрестности точки
Тейлора по степеням xi :
x
(0)
в ряд
R ( x1( 0 ) x1 , x 2( 0 ) x 2 , , x n( 0 ) x n ) R ( x ( 0 ) )
R
1 n n 2R
xi
2
i 1 x i
i 1 j 1 x i x j
(0)
x x
n
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
x i x j
x x (0)
Лекционный материал «Оптимизация ХТП»
V1.0 L1
25.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ25
с учётом необходимого условия существования экстремума:
R( x ) x x ( 0 ) R( x
( 0)
x ) R( x )
( 0)
dR( x ) x x ( 0 ) R( x ) x x ( 0 )
R
i 1 xi
n
dR( x ) x x ( 0 )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
xi 0
x x (0)
Лекционный материал «Оптимизация ХТП»
V1.0 L1
26.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ26
Если выражение
R
i 1 j 1 xi x j
n
n
2
xi x j
x x
(0)
сохраняет один и тот же знак для любых приращений
xi
то экстремум функции
РХТУ им. Д.И. Менделеева
x j
R (x ) в точке x ( 0 )
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
существует.
V1.0 L1
27.
27Приращение целевой функции в окрестности
экстремума определяется
R( x ( 0) ) R( x1( 0 ) x1 , x2( 0 ) x2 , , xn( 0) xn ) R( x ( 0 ) )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
28.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХОбозначив:
R
xi x j
28
2
aij
x x
(0)
xi zi
x j z j
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
29.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ29
получаем выражение вида:
R
R
i 1 j 1 xi x j
n
n
n
2
xi x j
x x
(0)
n
aij zi z j z
(2)
i 1 j 1
где
z
( 2)
- квадратичная форма.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
30.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ30
Условие положительной определённости квадратичной
формы (достаточных условий существования минимума):
при любых значениях
zi
и
z
а в точке
zi 0
и
( 2)
0
zj 0
z
РХТУ им. Д.И. Менделеева
zj 0
( 2)
Кафедра информатики и компьютерного проектирования
0
Лекционный материал «Оптимизация ХТП»
V1.0 L1
31.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ31
Квадратичная форма будет положительно определённой,
если все определители, составленные из элементов a ij
положительны (условия Сильвестра):
a11 0;
a11
a12
a21 a22
0;
a12
a21
a22 a2 n
an1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
a1n
a11
an 2 ann
Лекционный материал «Оптимизация ХТП»
V1.0 L1
0
32.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИИ
МНОГИХ ПЕРЕМЕННЫХ
32
Все определители Сильвестра положительны
(положительно определенная квадратичная форма):
R(
x
опт
)= min
Определители Сильвестра нечетного порядка
отрицательны, а четного порядка - положительны
(отрицательно определенная квадратичная форма):
R(
x
опт
)=
max
Иная последовательность чередования знаков
определителей Сильвестра:седловая точка=экстремума нет
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
33.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХДоказательство вышеприведенных
утверждений для 2-х переменных:
С учетом того, что:
1 R
a11 2
2 x1 x ( 0 )
2
1 R
a22 2
2 x2 x ( 0 )
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
33
34.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ34
и:
1 R
a12 a21
2 x1 x2 x ( 0 )
2
Квадратичная форма второго порядка записывается:
z
( 2)
a11 z 2 a12 z1 z2 a22 z
РХТУ им. Д.И. Менделеева
2
1
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
2
2
35.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ35
Преобразование последнего выражения приводит к
соотношению:
2
z
( 2)
a12 z 2
a 2
a22
z 2
a11 z1
a11
a11
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
2
12
V1.0 L1
36.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ36
Отсюда следует:
Квадратичная форма будет положительно определенной,
если:
a11 0
и:
2
12
a
a22
0
a11
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
37.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ37
Или в соответствии с условиями Сильвестра:
a11 0
и:
a11
a12
a21 a22
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
0
Лекционный материал «Оптимизация ХТП»
V1.0 L1
38.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ38
Квадратичная форма будет отрицательно определенной,
если:
a11 0
и:
2
12
a
a22
0; (*)
a11
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
39.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ39
Знак неравенства в последнем случае будет отрицателен,
когда числитель выражения после его приведения к общему
знаменателю будет положителен, так как a11 является
отрицательным числом
.
Из этого следует, что в соответствии с условиями Сильвестра
(учитывая, что a12 a21 ), квадратичная форма будет
отрицательно определенной в случае следующей системы
чередования знаков определителей:
a11 0;
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
a11
a12
a21 a22
Лекционный материал «Оптимизация ХТП»
V1.0 L1
0
40.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ40
Таким образом, достаточные условия экстремума функции
(0)
двух переменных в точке экстремума x
могут быть
сформулированы:
А)
R
2
x1
2
R
2
x1
2
R
2
x
(0)
2
x
2
РХТУ им. Д.И. Менделеева
x (0)
2R
x1 x2
Кафедра информатики и компьютерного проектирования
x (0)
x (0)
Лекционный материал «Оптимизация ХТП»
2
0
min
0
V1.0 L1
41.
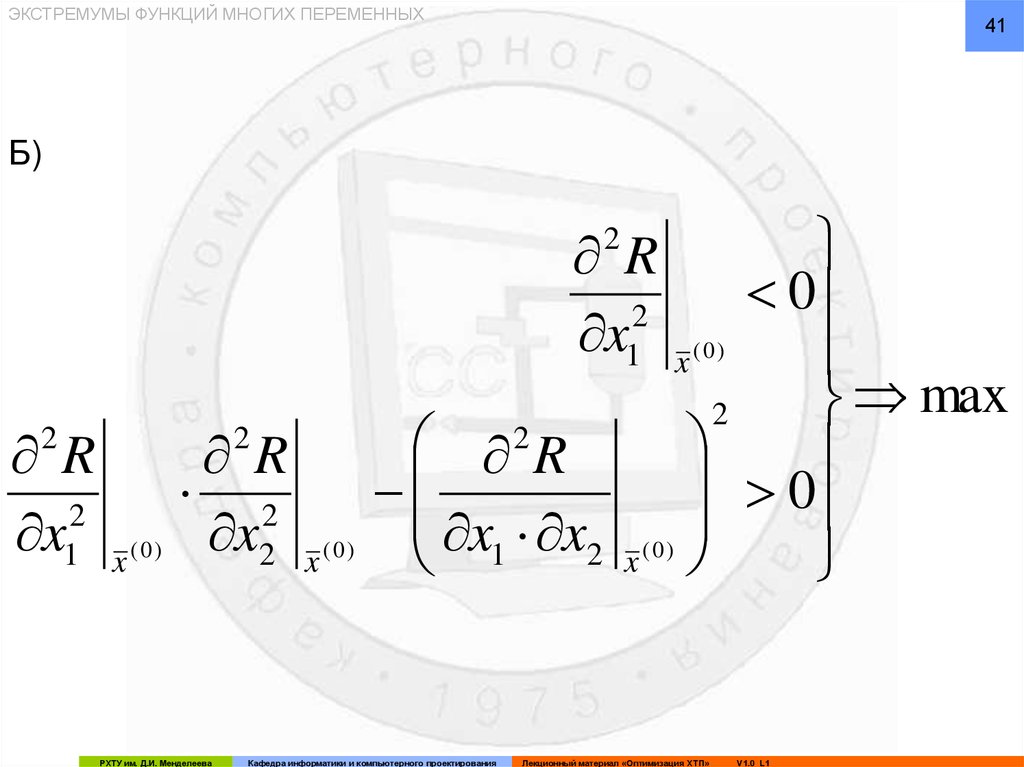
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ41
Б)
R
2
x1
2
R
2
x1
2
R
2
x
(0)
2
x
2
РХТУ им. Д.И. Менделеева
x (0)
2R
x1 x2
Кафедра информатики и компьютерного проектирования
x (0)
(0)
x
Лекционный материал «Оптимизация ХТП»
2
0
max
0
V1.0 L1
42.
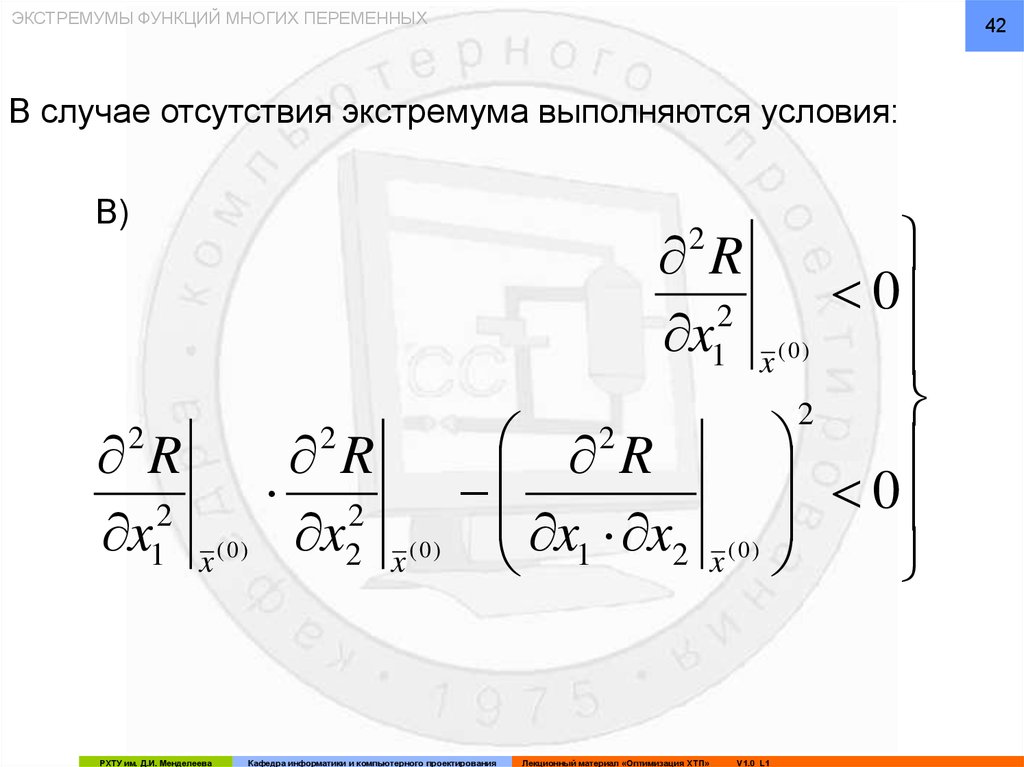
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ42
В случае отсутствия экстремума выполняются условия:
В)
R
2
x1
2
R
2
x1
2
R
2
x
(0)
2
x
РХТУ им. Д.И. Менделеева
2
x (0)
2R
x1 x2
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
x (0)
(0)
x
V1.0 L1
2
0
0
43.
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ43
Следует отметить, что аналитическая проверка достаточных
условий экстремума функции многих переменных не всегда
возможна.
В таких случаях прибегают к вычислительным
экспериментам на компьютере, либо вывод о существовании
экстремума может вытекать из физического смысла
решаемой задачи.
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
44.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
44
Рассмотрим химическую реакцию с целевым продуктом P,
проходящую по схеме:
aA bB
k1
pP qQ
k2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
45.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ45
Скорость реакции по целевому продукту выражается по
закону действующих масс:
W k x x k x x
a b
1 A B
p q
2 P Q
Необходимо определить температуру T проведения реакции,
при которой:
W Wmax
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
46.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ46
Необходимое условие экстремума:
dW
0
dT
dk1
p q dk 2
x x
xP xQ
0
dT
dT
a b
A B
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
47.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ47
k j A j exp( E j RT )
dk j
dT
[ A j exp(
dk j
dT
РХТУ им. Д.И. Менделеева
kj
Кафедра информатики и компьютерного проектирования
Ej
RT
)]
Ej
RT
Ej
RT
2
Лекционный материал «Оптимизация ХТП»
V1.0 L1
2
48.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙa b
A B 1
x x k (T
опт
48
E1
E2
p q
опт
)
x
x
k
(
T
)
0
P
Q
2
2
2
RT
RT
опт
p q
P Q
a b
A B
E1k1 (T ) x x
опт
E2 k 2 (T ) x x
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
49.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ49
В состоянии равновесия скорость реакции W равна 0:
W 0
x x k (Tравновесн. ) x x k (Tравновесн. ) 0
a b
A B 1
РХТУ им. Д.И. Менделеева
p q
P Q 2
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
50.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ50
k1 (Tравновесн. )
k2 (Tравновесн. )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
p q
P Q
a b
A B
x x
Лекционный материал «Оптимизация ХТП»
x x
V1.0 L1
51.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ51
Получаем связь равновесной и оптимальной температур
проведения реакции:
опт
E1k1 (T ) k1 (Tрав новесн. )
опт
E2 k 2 (T ) k 2 (Tрав новесн. )
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
52.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ52
E1 A1 exp( E1 RT ) A1 exp( E1 RT рав нов есн. )
опт
E2 A2 exp( E2 RT ) A2 exp( E2 RT рав нов есн. )
опт
откуда:
E2 E1 E1
E
E
2
1
exp
exp
опт
RT
E
RT
рав
новесн
.
2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
53.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ53
После логарифмирования получаем:
E2 E1
E2 E1
E1
ln
опт
RT равновесн. RT
E2
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1
54.
ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ54
Откуда следует:
T
опт
Tрав нов есн.
RT рав нов есн.
E2
1
ln
E2 E1
E1
РХТУ им. Д.И. Менделеева
Кафедра информатики и компьютерного проектирования
Лекционный материал «Оптимизация ХТП»
V1.0 L1




































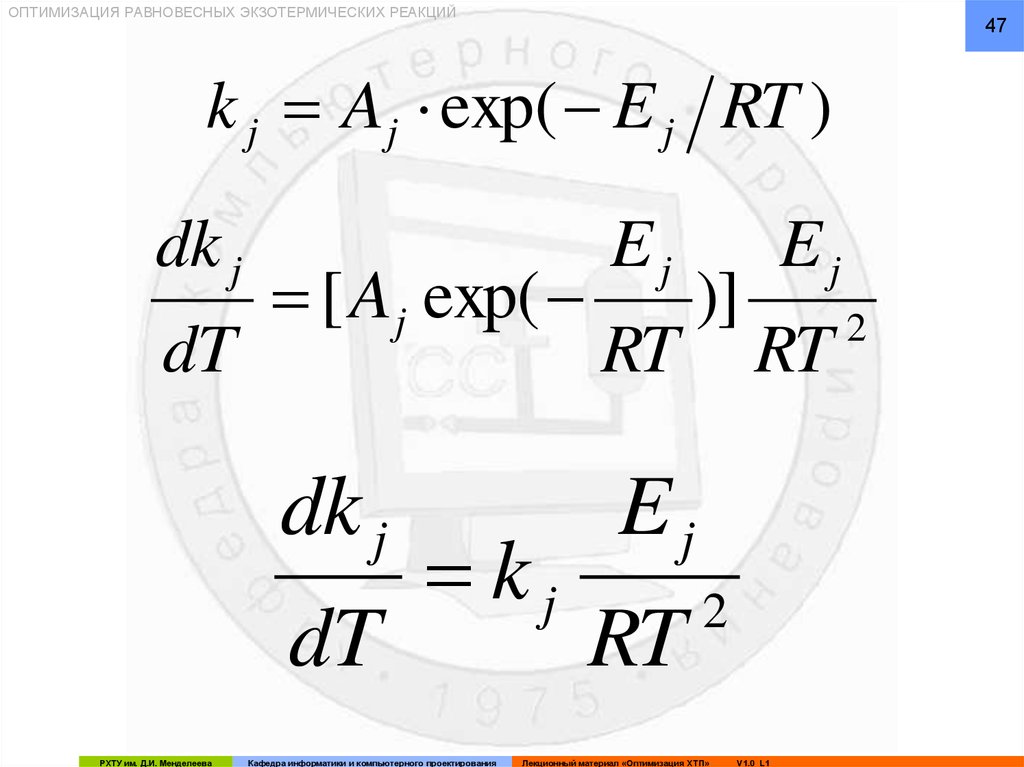







 Математика
Математика