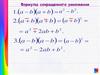Похожие презентации:
Формулы сокращенного умножения
1. Формулы сокращенного умножения.
Учитель математики МАОУ лицей №3города Кропоткин Краснодарского края
Зозуля Елена Алексеевна
2. Кто ввел понятие о формулах сокращенного умножения?
Формулы сокращённого умножения многочленов —часто встречающиеся случаи умножения
многочленов. Многие из них являются частным
случаем Бинома Ньютона.
Изучаются в средней школе в курсе алгебры.Бино́м
Нью́то́на — формула для разложения на отдельные
слагаемые целой неотрицательной степени суммы
двух переменных
Долгое время считалось, что для натуральных
показателей степени эту формулу, как и
треугольник, позволяющий находить
коэффициенты, изобрёл Блез Паскаль, описавший
её в XVII веке.
3.
Однако историки науки обнаружили, что формулабыла известна ещё китайскому математику Яну
Хуэю, жившему в XIII веке, а также исламским
математикам ат-Туси (XIII век) и ал-Каши (XV век).
Исаак Ньютон около 1676 года обобщил формулу
для произвольного показателя степени (дробного,
отрицательного и др.). Из биномиального
разложения Ньютон, а позднее и Эйлер,
выводили всю теорию бесконечных рядов.
4.
Очень часто приведение многочлена кстандартному виду можно осуществить
путём применения формул сокращённого
умножения . Все они доказываются
непосредственным раскрытием скобок и
приведением подобных слагаемых.
Формулы сокращённого умножения нужно
знать наизусть!!!
5. Формулы сокращенного умножения для квадратов:
(a b) a 2ab b2
(a b) a 2ab b
2
2
2
2
2
a b (a b)( a b)
2
2
(a b c) a b c 2ab 2ac 2bc
2
2
2
2
6. Формулы сокращенного умножения для кубов:
(a b) 3 a 3 3a 2b 3ab 2 b 3(a b) a 3a b 3ab b
3
3
2
2
3
a b (a b)( a ab b )
3
3
2
2
a 3 b 3 (a b)( a 2 ab b 2 )
(a b c) a b c 3a b 3a c
3
3
3
3
2
2
3ab 3ac 3b c 3bc 6abc
2
2
2
2
7. Формулы сокращенного умножения для четвертой степени:
(a b) a 4a b 6a b 4ab b4
4
3
2 2
3
(a b) a 4a b 6a b 4ab b
4
4
3
2 2
3
4
4
a b (a b)(a b)(a b )
4
4
2
2
a b (a 2ab b )(a 2ab b )
4
4
2
2
2
2
a a b b (a ab b )(a ab b )
4
2 2
4
2
2
2
2
8. Формулы сокращенного умножения для n-ой степени:
a b (a b)(an
n
n 1
a
n 2
b a
n 3 2
b ..
. a 2b n 3 ab n 2 ab n 1 )
a b (a b)(a
n
n
2 n 3
. a b
a b
2n
2n
n 1
a
ab
n 2
n 2
b a
ab
n 3 2
n 1
b ..
)
(a b )( a b )
n
n
n
n
9. Задачи
1.Представить в видемногочлена
(x 5)
2
2
10.
Применяем формулуквадрата разности и
получаем:
(x ) 2x
2 2
2
5 ( 5 ) x 2 5x 5
2
4
2
11.
2. Представить ввиде многочлена :
( 3 x)( x 3)( x 3 )
2
12.
Очевидно, что можно решить задачу открывпервые две скобки, далее последующие
две. Но, если присмотреться, можно
заметить более простой путь к решению
задачи. А именно - занеся минус в первые
скобки и открыв крайние мы получим
квадрат разности, который легко
преобразуется в многочлен:
( 3 x)( x 2 3)( x 3 ) ( x 3 )( x 3 )( x 2 3) ( x 2 3)( x 2 3)
( x 3) x 6 x 9
2
2
4
2
13.
3.Подставить вместомноготочия одночлены
так, чтобы
выполнялось
равенство:
(15x ...) ... ... 50 y
2
14.
Согласно формуле сокращенного умноженияквадрата разницы найдем второй член в
равенстве слева. Его квадрат равен 50y, а,
значит, недостающий одночлен равен
50 y 2 25 y 5 2 y
Левая часть равенства определена, теперь
нам не составит труда заполнить остальные
многоточия. (15 х) 2 225 х 2 - первый одночлен
правой части
найден. Найдем и
второй:
2 15х 5 2 у 150х 2 у
15.
(15х 5 2 у )2
225х 150 х 2 у 50 у
2
16.
4. Преобразуйте вмногочлен
выражение:
( х 6)( х 6 х 36) 2( х 3)( х 3)
2
17.
( х 6)( х 6 х 36) 2( х 3)( х 3) ( х 216) 2( х 9)2
3
2
х 216 2 х 18 х 2 х 234
3
2
3
2
18. Список литературы:
1.Википедия2.”Только факты” под
редакцией Ридерс Дайджест.
3. www.Grandars.ru


















 Математика
Математика