Основные понятия тригонометрии: радианная мера угла, вращательное движение, синус, косинус, тангенс, котангенс угла

1. Тема урока:

”Основные понятия тригонометрии:
радианная мера угла, вращательное
движение, синус, косинус, тангенс,
котангенс угла”

2. Цели урока:

рассмотреть понятия радианной меры угла,
вращательного движения, синуса, косинуса,
тангенса, котангенса угла, основные
тригонометрические тождества, формулы
приведения
формировать умения применять
тригонометрические тождества, формулы
приведения

3.

Что такое тригонометрия?
Тригономе́трия (от др.греч. τρίγωνον «треугольник»
и μετρέω «измеряю») — раздел математики, в
котором изучаются тригонометрические
функции и их использование в геометрии.
Данный термин впервые появился в 1595 г. как
название книги немецкого
математика Бартоломеуса Питискуса, а сама
наука ещё в глубокой древности
использовалась для расчётов в астрономии,
архитектуре и геодезии для вычисления одних
элементов треугольника по данным о других
его элементах.

4.

Рассмотрим окружность радиуса R
и отметим на ней дугу РМ длины R и
угол РОМ.
Центральный угол, опирающийся на дугу, длина которой
равна радиусу окружности, называется углом в один радиан.
Градусная мера угла в 1 радиан равна:
Так как π = 3,14, то 1 рад ≈57,3°.
Если угол содержит а радиан, то его градусная мера равна:

5.

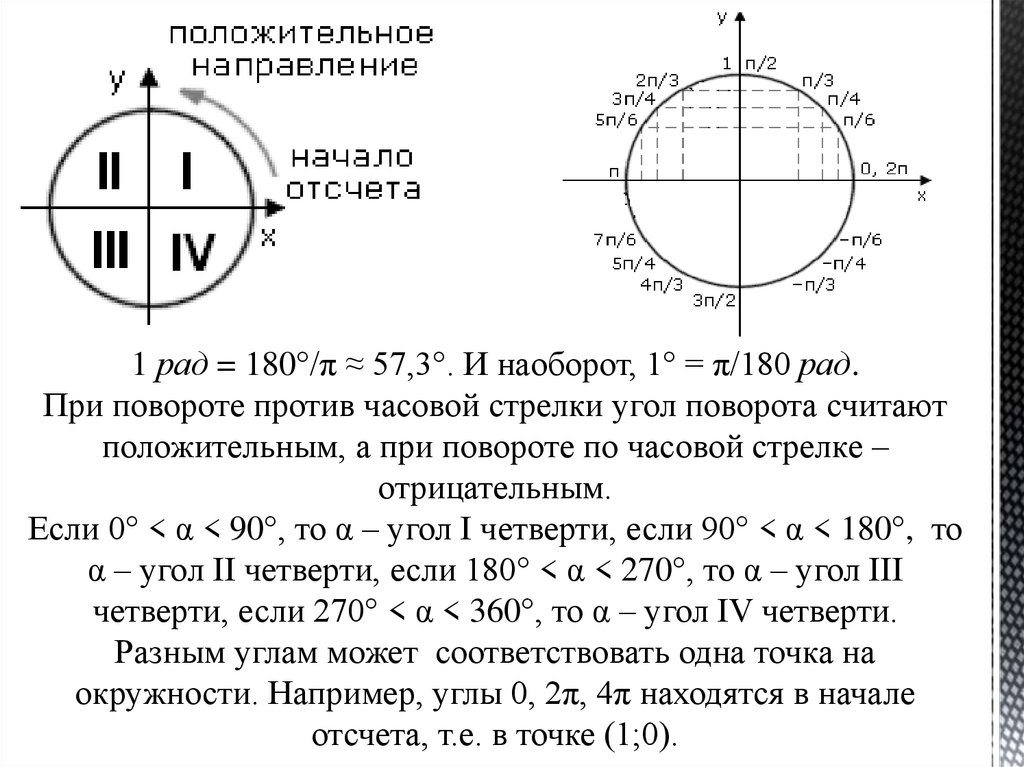
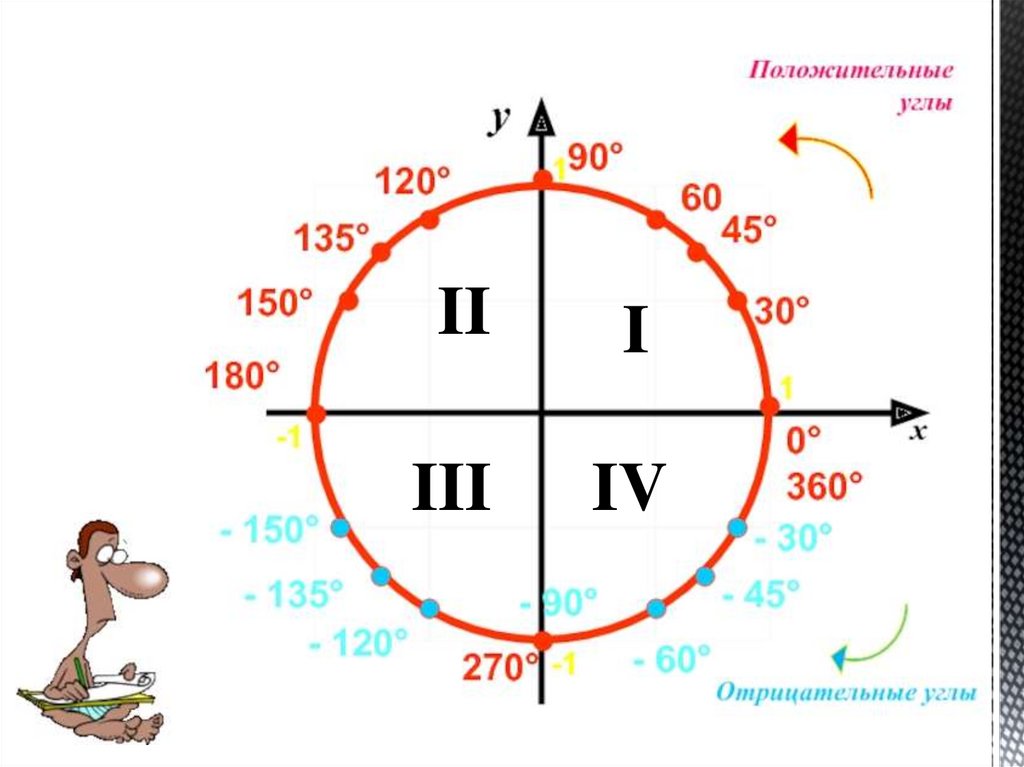
1 рад = 180°/π ≈ 57,3°. И наоборот, 1° = π/180 рад.
При повороте против часовой стрелки угол поворота считают
положительным, а при повороте по часовой стрелке –
отрицательным.
Если 0° < α < 90°, то α – угол I четверти, если 90° < α < 180°, то
α – угол II четверти, если 180° < α < 270°, то α – угол III
четверти, если 270° < α < 360°, то α – угол IV четверти.
Разным углам может соответствовать одна точка на
окружности. Например, углы 0, 2π, 4π находятся в начале
отсчета, т.е. в точке (1;0).

6.

II
I
III
IV

7.

Синусом угла α называется отношение ординаты
точки A к длине отрезка OA. Обозначают
sin α = OC/OA. Так как длина отрезка OA = 1, то
sin α = ОC=у.
Косинусом угла α называется отношение
абсциссы точки A к длине отрезка OA.
Обозначают cos α = OB/OA. Так как длина отрезка
OA = 1, то cos α = OB=х
Тангенсом угла α называется отношение ординаты точки A к абсциссе
точки A. Обозначают tg α = OC/OB. Так как OC = sin α, OB = cos α, то
tg α = sin α/cos α.
Котангенсом угла α называется отношение абсциссы точки A к
ординате точки A. Обозначают ctg α = OB/OC. Так как OC = sin α,
OB = cos α, то ctg α = cos α/sin α.
Котангенс равен обратному значению тангенса: ctg α = 1/tg α.
Из определения следует: если cos α = 0, то тангенс этого угла (α) не
существует. Аналогично для котангенса: если sin α = 0, то котангенс этого
угла (α) не существует.

8.

Значение тригонометрических функций для
некоторых углов

9.

Функция cos является
четной функцией.
Функции: sin, tg, ctg –
нечётные функции.
cos (-x) = cos x;
sin (-x) = - sin x; cos (-300) = cos 300;
0) = - sin 450;
sin
(-45
tg (-x) = - tg x;
0) = - tg 600;
tg
(-60
ctg (-x) = - ctg x.
ctg (-750) = - ctg 750.

10.

11.

Задача 1. Найдите градусную меру угла равного π радиан,
π/2 радиан, 3π/4 рад.
Решение: по формуле:
180
рад
0
π радиан = 1800; π/2 радиан = 900, 3π/4 рад = 1350.
Найдём радианную меру угла в 10. Так как угол 1800 равен π
радиан, то: 0
1
180
рад
Если угол содержит α градусов, то его радианная мера
составляет:
0
180
рад

12.

Задача 2. Найдите радианную меру угла равного 450, 150
Решение:
0
180
45
0
15
0
180
180
45 рад
15 рад
4
12
рад
рад

13.

Площадь кругового сектора радиуса R, образованного
углом в π рад, равна:
R2
S
, где 0
2
Длина дуги, радиуса R, стягиваемая центральным углом α,
вычисляется по формуле:

14.

.
Задача 3. Найти радианную меру угла, выраженного в
градусах: 1) 40°; 2) 120°; 3) 150°
Задача 4. Найти градусную меру угла, выраженного в
радианах: 3
; ;2;3;0,36
6 9 4
;

15.

Задача 5. Вычислить радиус окружности, если дуга
длиной 0,36 м стягивает центральный угол в 0,9 рад.
Задача 6. Найти радианную меру угла, стягиваемого дугой
окружности длиной 3 см, если радиус окружности равен 1,5
см.

16.

Задача 7. Дуга кругового сектора стягивает угол в 3π/4
рад. Найти площадь сектора, если радиус круга равен 1 см.
Задача 10. Определите в какой четверти заключается угол α,
если: а) α = 1200; б) α = 4350; в) α = - 2800
Задача 14. Найдите значение выражения: