Простейшие векторные операции и их реализация на языке MATLAB

1.

Простейшие векторные операции
и их реализация на языке
MATLAB
E-mail: [email protected]
сот: 8-910-443-75-52
Подготовил: Смирнов П.А.

2.

Векторные операции
Вектор в трёхмерном пространстве
Координаты точки начала
Координаты точки конца
Координаты вектора
M1(Х1,Y1,Z1)
M2(Х2,Y2,Z2)
V(Х2-X1,Y2-Y1, Z2-Z1)=V(X,Y,Z)
V
Вектор
Сумма векторов
VΣ ( X12 X11 ) ( X 22 X 21 ),(Y12 Y11 ) (Y22 Y21 ),(Z12 Z11 ) (Z22 Z21 )
VΣ ( X1 X 2 ),(Y1 Y2 ),(Z1 Z2 )
VΣ V1 + V2
V
V1
V2
Разность векторов
V1 2 ( X12 X11 ) ( X 22 X 21 ),(Y12 Y11 ) (Y22 Y21 ),(Z12 Z11 ) (Z22 Z21 )
V1 2 ( X1 X 2 ),(Y1 Y2 ),(Z1 Z2 )
V1 2 V1 V2
V1
V1 2
V2

3.

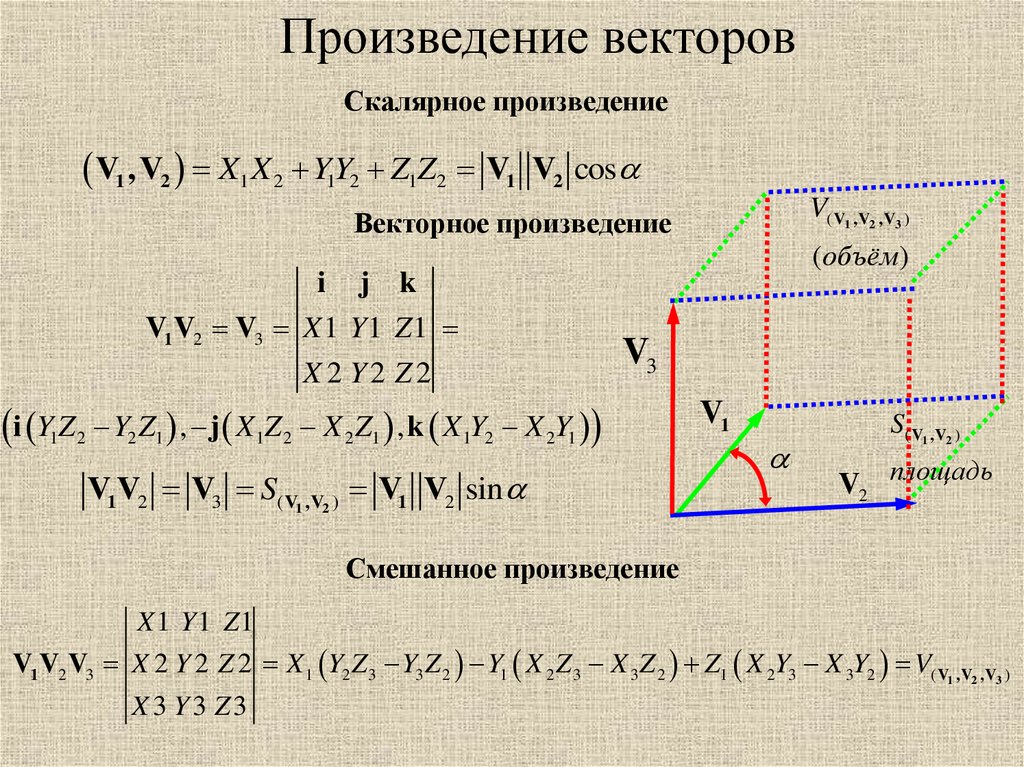
Произведение векторов
Скалярное произведение
V1 , V2 X1 X 2 YY
1 2 Z1Z 2 V1
V2 cos
V( V1 ,V2 ,V3 )
Векторное произведение
(объём)
i
j k
V1V2 V3 X 1 Y 1 Z1
X 2 Y2 Z2
i Y Z
1
2
V3
Y2 Z1 , j X 1Z 2 X 2 Z1 , k X 1Y2 X 2Y1
V1V2 V3 S( V1 ,V2 ) V1 V2 sin
V1
S( V1 ,V2 )
V2 площадь
Смешанное произведение
X 1 Y 1 Z1
V1 V2 V3 X 2 Y 2 Z 2 X 1 Y2 Z 3 Y3 Z 2 Y1 X 2 Z 3 X 3 Z 2 Z1 X 2Y3 X 3Y2 V( V1 ,V2 ,V3 )
X 3 Y3 Z3

4.

Что даёт узнать блок с помощью векторных операций?
V
2
1
Площадь любой из граней S
(1, 2,3,4)
12
Объём блока
Длину любого
из рёбер
Любую из характеристик
любого из углов
, V23 V34 , V41
1
Vблока ((V51 , V12 , V23 )
3
(V51 , V34 , V41 ))
Любую из нормалей к
поверхностям блока

5.

Вектор как объект
Свойства вектора
Возможные методы вектора
Координаты точки начала
Суммирование
Координаты точки конца
Координаты вектора
Модуль (длина) вектора
Скалярное произведение
Векторное произведение
Определение косинуса
между векторами
Определение синуса между
векторами
sin
V1V2
V1 V2
V1 , V2
;cos
V1V2
tg
;
V1 , V2
V1 V2
V1 , V2
ctg
V1V2
e
e
i
V1V2
V1 , V2
cos i sin
i
V1 V2
i
V1 V2
V1V2
V1 , V2
cos i sin
i
V1 V2
V1 V2