Работа с матрицами и решение систем линейных алгебраических уравнений

1.

Обязательный базовый раздел:
С 23 сентября по 6 октября – 2 недели
15 минут на прохождение (с любого IP, не
обязательно Политехского)
2 попытки
70%-ный порог прохождения теста
Тест №2:
С 23 сентября по 6 октября – 2 недели
90 минут на прохождение (с IP Политеха, под
руководством преподавателя!!!)
1 попытка

2.

3.

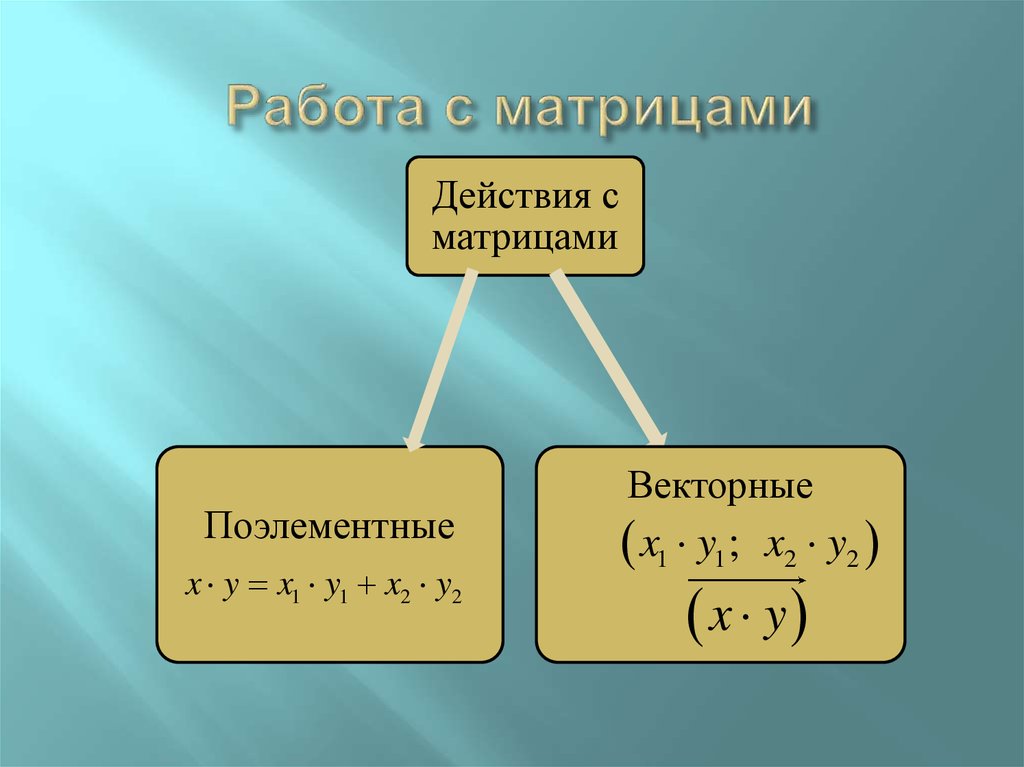
Действия с
матрицами
Поэлементные
x y x1 y1 x2 y2
Векторные
x1 y1;
x2 y2
x y

4.

5.

Строка
Элемент
Столбец

6.

Индексация
элементов начинается
с 0!!!
Индексы:
Строка (1), столбец (0)
ORIGIN:=1

7.

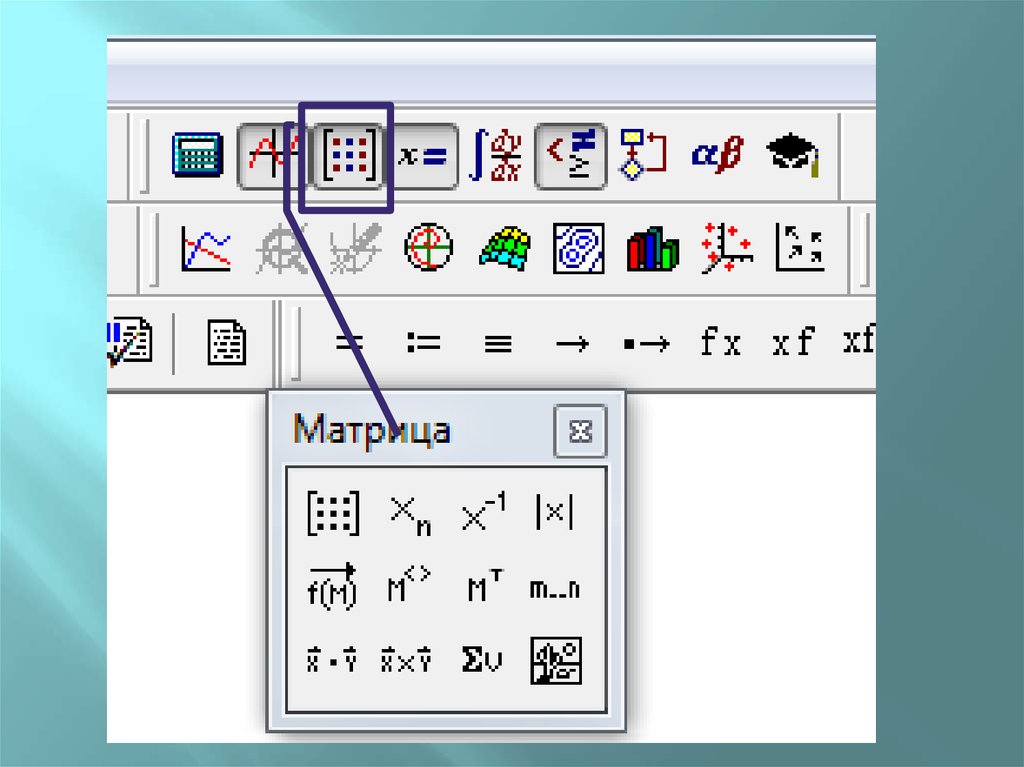
1 – вставка матрицы
заданного размера
2 – индекс, обращение
к элементу матрицы
3 – обратная матрица
4 – определитель
5 – столбец матрицы
6 – транспонированная
матрица
7 – диапазон изменения
переменной
8 – сума компонентов
вектора

8.

det M
определитель
tr M
след
rang M
rg ( M )
Ранг
M
Число обусловленности
M
Норма
тип

9.

10.

11.

12.

m
max ij
i
l max ij
j
i
e
j
2
ij
j

13.

14.

15.

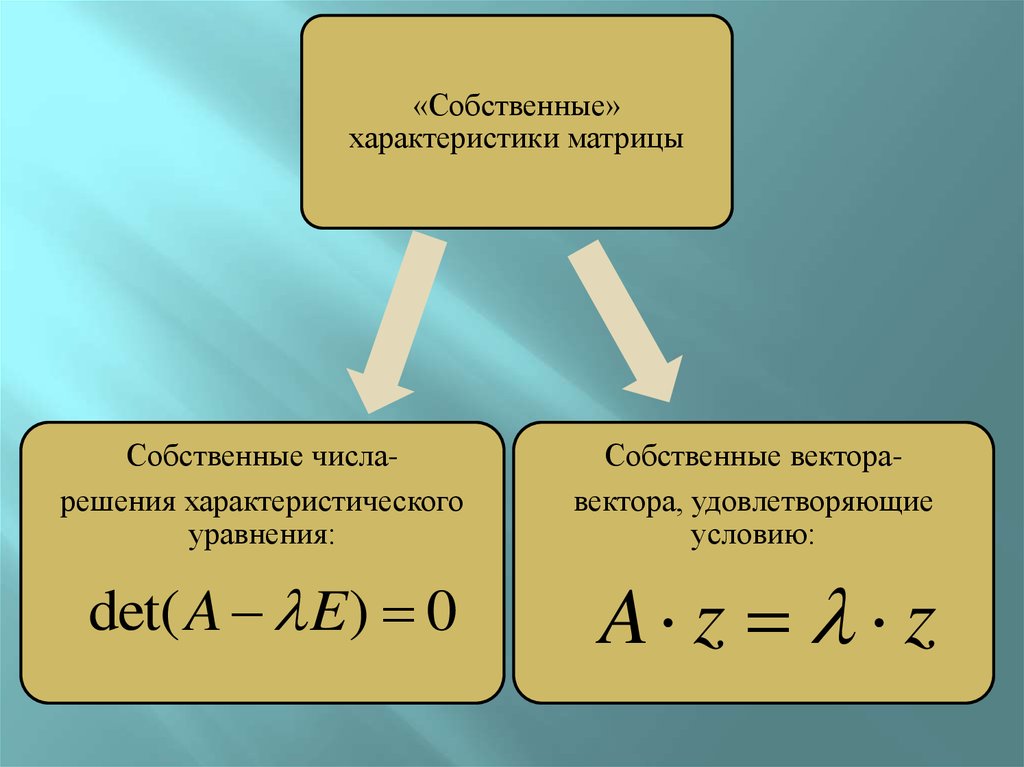
«Собственные»
характеристики матрицы
Собственные числарешения характеристического
уравнения:
Собственные векторавектора, удовлетворяющие
условию:
det( A E) 0
A z z

16.

det( A E) 0

17.

Вычисление
«собственных» характеристик
матрицы
Собственные числаeigenvals (A)
Собственные вектораeigenvecs (A) найдет
все собственные
вектора матрицы А.

18.

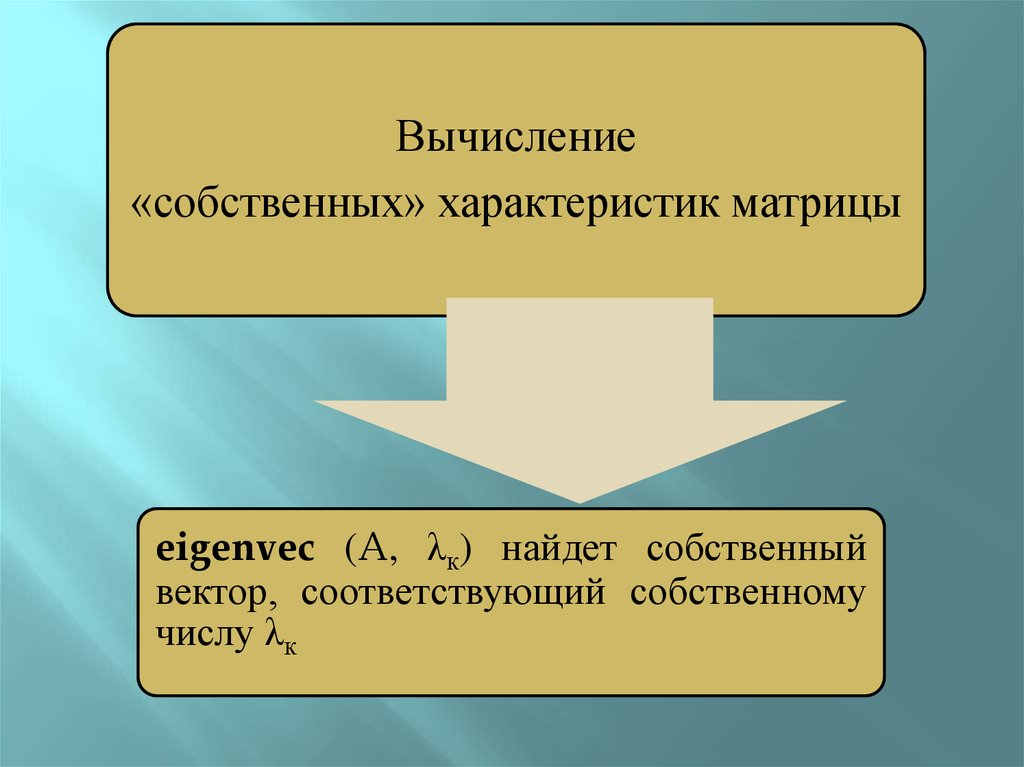
Вычисление
«собственных» характеристик матрицы
eigenvec (A, λк) найдет собственный
вектор, соответствующий собственному
числу λк

19.

A k z k z

20.

21.

22.

23.

24.

25.

26.

27.

28.

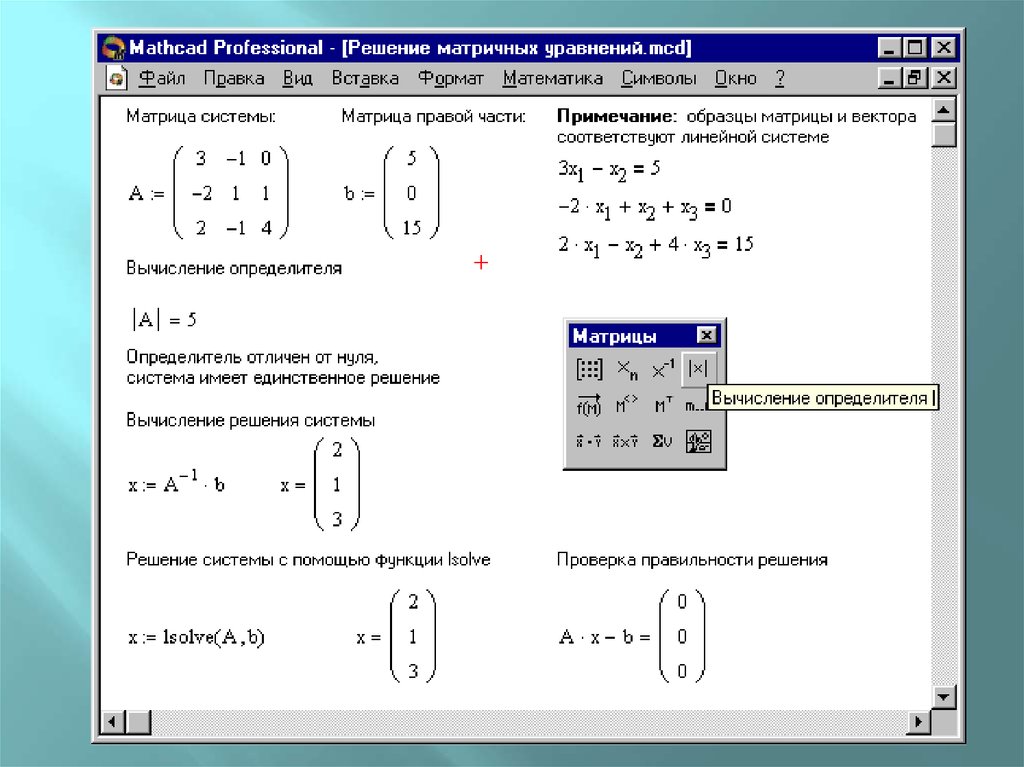
a11 x1 a12 x2 a13 x3 ... a1n xn b1
a x a x a x ... a x b
21 1 22 2
23 3
2n n
2
...
an1 x1 an 2 x2 an 3 x3 ... ann xn bn
a11
a
12
A
...
an1
a12
a22
...
an 2
... a1n
... a2 n
... ...
... ann
b1
b
2
b
...
bn

29.

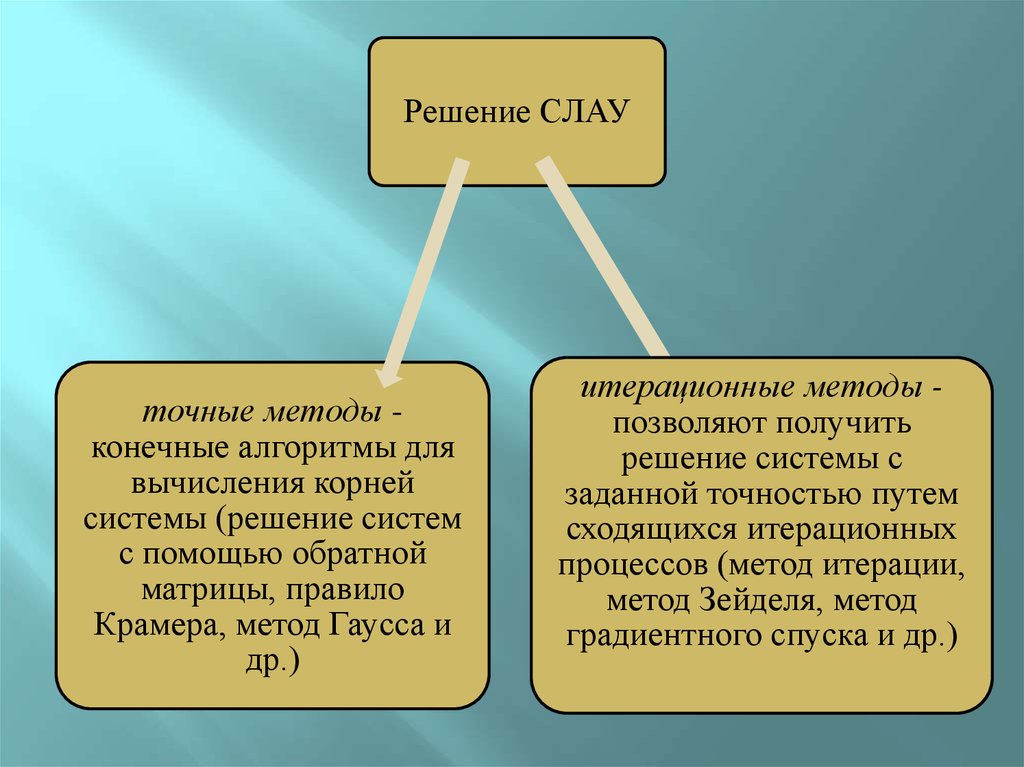
Решение СЛАУ
точные методы конечные алгоритмы для
вычисления корней
системы (решение систем
с помощью обратной
матрицы, правило
Крамера, метод Гаусса и
др.)
итерационные методы позволяют получить
решение системы с
заданной точностью путем
сходящихся итерационных
процессов (метод итерации,
метод Зейделя, метод
градиентного спуска и др.)

30.

Решение СЛАУ
Вследствие неизбежных
округлений результаты
даже точных методов
являются приближенными
Эффективное применение
итерационных методов
существенно зависит от
удачного выбора начального
приближения и быстроты
сходимости процесса

31.

32.

33.

x1 12 x2 13 x3 ... 1n xn 1
x2 23 x3 ... 2 n xn 2
...
xn n
xn n
xi i
n
j i 1
ij
x j i n 1, n 2,...1