Похожие презентации:
Структура изображения
1. Структура изображения
Будак Владимир Павлович,НИУ «МЭИ»
кафедра светотехники
: +7 (495) 763-5239
BudakVP@mpei.ru
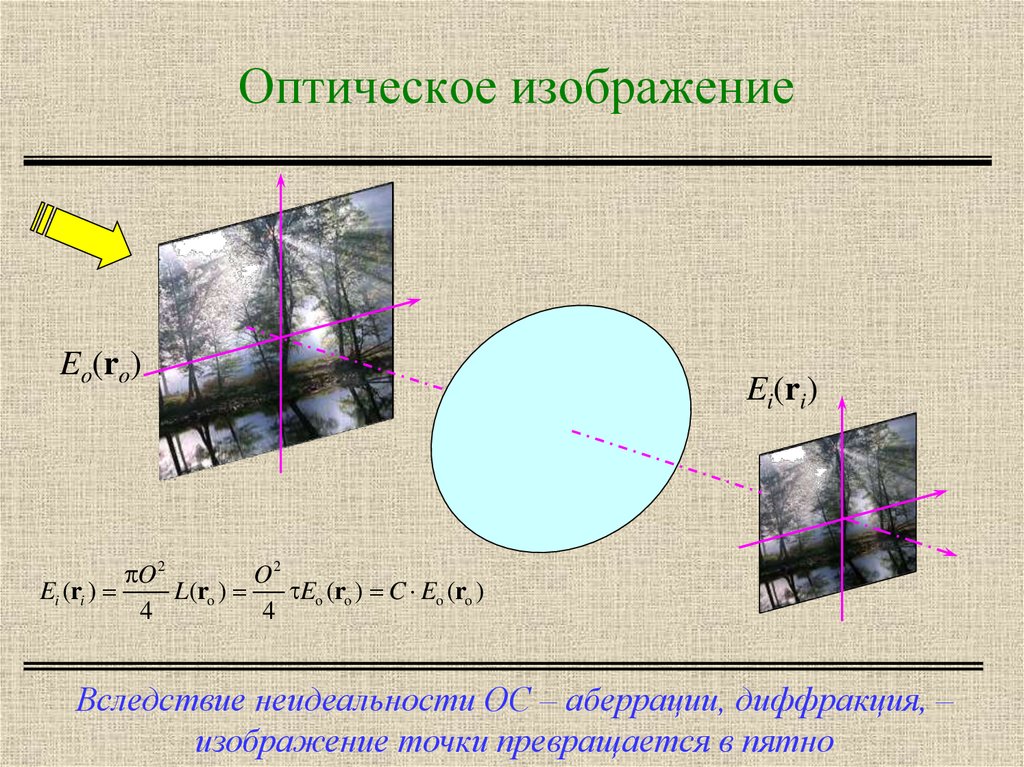
2. Оптическое изображение
Eo(ro)Ei(ri)
O 2
O2
Ei (ri )
L(ro )
Eo (ro ) C Eo (ro )
4
4
Вследствие неидеальности ОС – аберрации, диффракция, –
изображение точки превращается в пятно
3. Свертка – convolution
h(ro→ri) – функция рассеяния точки (ФРТ, Point SpreadFunction, PSF) – распределение облученности в
изображении от светящейся точки объекта
Ei (ri ) Eo (ro )h(ri ro)d 2 ro
• ФРТ не зависит от абсолютного положения точки в
плоскости объекта – системы инвариантные к сдвигу
• Интеграл суперпозиции переходит в интеграл свертки
Ei (ri ) Eo (ro )h(ri ro)d 2 ro Eo (r ) * h(r)
Распределение облученности в плоскости изображения связано с
распределением облученности плоскости анализа через свертку
4. Фурье-оптика (Fourier)
• Duffieux P.М. L’Intégrale de Fourier et ses Applications à L’Optique.– Besançon, 1946
• Schade О.H. Electro- optical characteristics of television systems //
RCA Rev., 9, 5 (Part I), 245 (Part II), 490 (Part III), 653 (Part IV)
(1948)
• Марешаль А., Франсон М. Структура оптического изображения.
– М.: Мир, 1964
• О'Нейл Э. Введение в статистическую оптику. – М.: Мир, 1966
• Гудмен Дж. Введение в фурье-оптику. – М.: Мир, 1970
• Папулис А. Теория систем и преобразований в оптике. М.: Мир,
1971
С позиций светового (лучевого) поля также возможен вывод
уравнения свертки, но сложнее и выполнен позднее
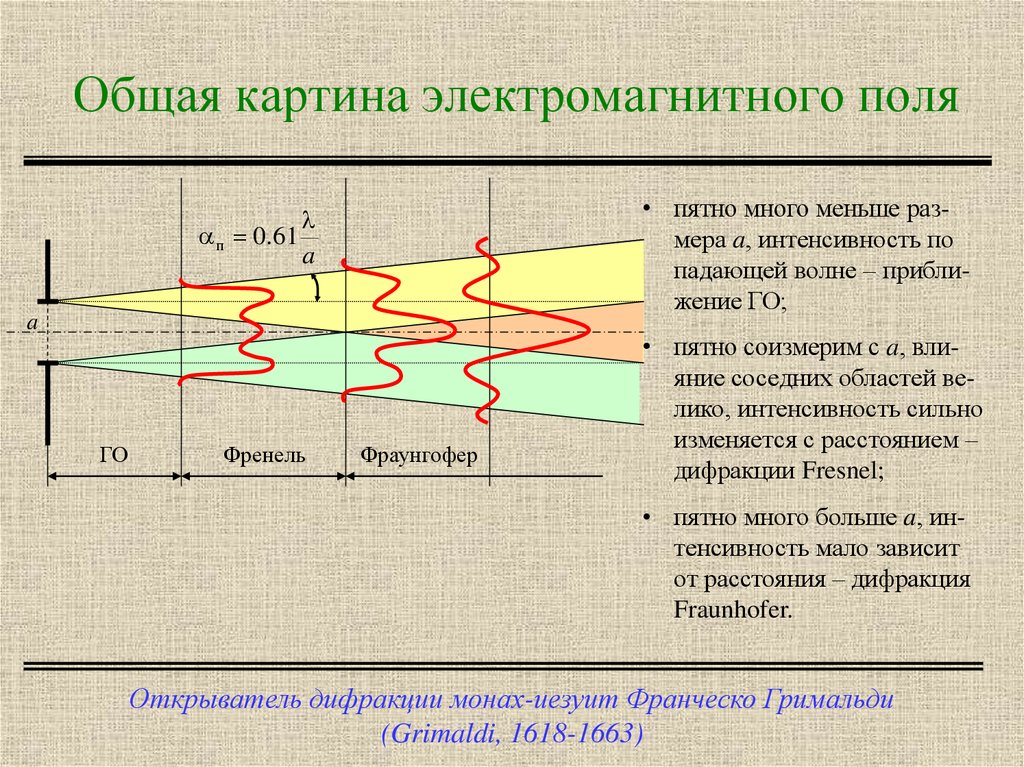
5. Общая картина электромагнитного поля
• пятно много меньше размера a, интенсивность попадающей волне – приближение ГО;
п 0.61
a
a
ГО
Френель
Фраунгофер
• пятно соизмерим с a, влияние соседних областей велико, интенсивность сильно
изменяется с расстоянием –
дифракции Fresnel;
• пятно много больше a, интенсивность мало зависит
от расстояния – дифракция
Fraunhofer.
Открыватель дифракции монах-иезуит Франческо Гримальди
(Grimaldi, 1618-1663)
6. Поле в плоскости анализа ОС
U0(z)Fresnel
Ul(ρ) → U´l(ρ)
Fresnel
Uo(ρ) =τ (ρ)U0
so
si
Ui(ρ)
Для анализа ОС дифракцию Fresnel можно считать точным
решением скалярного волнового уравнения
7. Оптическая передаточная функция
Для систем инвариантных к сдвигу можно предложить иное разбиениевходного сигнала на элементарные, что приведет к иной формулировки
принципа суперпозиции
Ei (k ) Ei (r )eikr d 2 r , Eo (k ) Eo (r)eikr d 2r , H (k ) h(r)eikr d 2r
Ei (ri ) Eo (ro )h(ri ro)d 2 ro
ikri 2
ikri
2
2
2
E
(
r
)
h
(
r
r
)
d
r
e
d
r
E
(
r
)
h
(
r
r
)
e
d
r
d
ro
o
o
i
o
o
i
o
o
i
o
i
E (r ) h(r r )e
o
ri ro :
o
i
o
ikri ikro ikro
d 2 ri d 2 ro Eo (ro ) eikro h(ri ro)eik (ri ro ) d 2 ri d 2 ro
ikro
ikro
ik 2
2
2
ik 2
E
(
r
)e
h
(
)
e
d
d
r
E
(
r
)e
d
r
h
(
)
e
d Eo (k ) H (k )
o
o
o
o
o
o
Ei (k ) Eo (k ) H (k )
Преобразование Fourier переводи свертку в произведение
Optical Transmittance Function
8. Пространственные гармоники
eikx e ikxsin kx
2i
cos kx
eikr e ikr
sin(kx ky ) sin kr
2i
e e
2
ikx
ikx
eiky e iky
sin ky
2i
eikr e ikr
cos(kx ky ) cos kr
2
Пространственные гармоники
– специальные элементарные сигналы
9. Пространственный спектр изображения
MИсходное N=256
M=8
ilk 0r
E
(
r
)
c
e
i
l
M=1
M=2
l 0
M=16
M=32
M=4
M=64
Пространственный спектр – разложение изображения на
сумму элементов: пространственных гармоник
10. Преобразование спектра линейной системой
1.8I
1.6
I max I min
I I
, I max min
2
2
1.4
K
1.2
1
0.8
I I max I min
I
I max I min
I o ( x) I o I o sin(kx), I i ( x) I i I i sin(kx)
0.6
0.4
Ki
0.2
0
0
1
2
3
4
5
H (k ) I o H (k )
H (k )
I i
K o , T (k )
Ii
H (0) I o
H (0)
H (0)
6
• |H(k)| - модуляционная передаточная функция (МПФ)
• argH(k) – фазовая передаточная функция (ФПФ)
Нормированная МПФ характеризует передачу контраста в
изображении
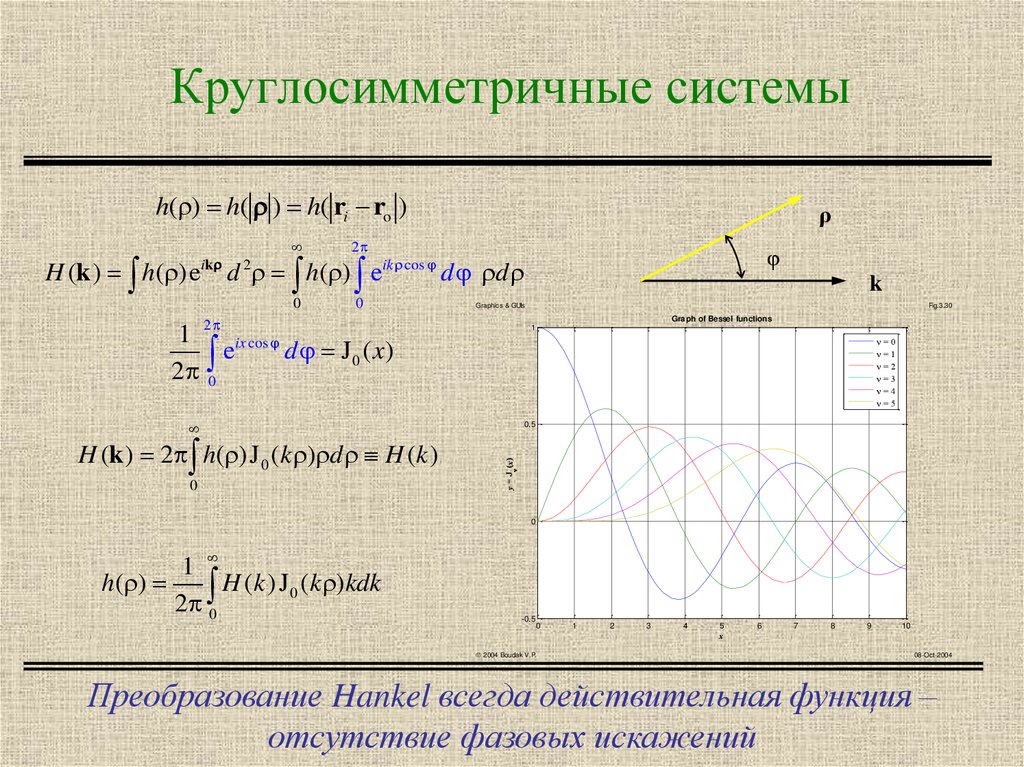
11. Круглосимметричные системы
h( ) h( ) h( ri ro )H (k ) h( )e
ik
2
0
0
ρ
φ
d h( ) eik cos d d
2
k
Graphics & GUIs
2
Fig.3.30
Graph of Bessel functions
1
eix cos d J 0 ( x)
2 0
1
=0
=1
=2
=3
=4
=5
0
H (k ) 2 h( ) J 0 ( k ) d H (k )
y = J (x )
0.5
0
1
h( )
H (k ) J 0 (k )kdk
2 0
-0.5
0
2004 Boudak V.P.
1
2
3
4
5
x
6
7
8
9
10
08-Oct-2004
Преобразование Hankel всегда действительная функция –
отсутствие фазовых искажений
12. Система
Пусть имеется набор элементов f F и g G, G, F – линейные пространства:g1,g2 G и f1,f2 F
g1 g2 G, g1 G, f1 f 2 F, f1 F
где - комплексное число.
Система – правило сопоставление элементов из
одного пространства элементам другого
g G f F : f Tg
1.
2.
3.
4.
g G
T
f F
F G – преобразование;
если ( g G)( f F) и при этом f – единственное и наоборот, то
отображение называется взаимно-однозначным;
если g=g(t), f=f(t), то система называется одномерным, если g=g(x,y) g(r)
и f=f(x,y) f(r), то система двумерная, а ее сигналы принято называть
полями;
сигналы могут быть как скалярами, так и векторами (матрицами).
Система осуществляет отображение пространства входных
сигналов в пространство выходных
13. Линейная система
если множество выходных сигналов первой системы является подмножествомвходных сигналов второй системы, то
f 2 T2 g2 T2 f1 T2T1g1 Tg1
g2 G2
g1 G1
T1
f2 F2
T2
f1 F1
то есть любую составную систему всегда можно заменить одной системой
Описание систем значительно упрощается, если система линейная. Система
называется линейной, если
N
N
gi G i : L i gi i L( gi )
i 1
i 1
Является математической формулировкой принципа
суперпозиции










 Физика
Физика








