Похожие презентации:
Осевая симметрия
1. Осевая симметрия.
Работу выполнила ученица 11 «В»класса
Жамбалова Арина
Педагог: Подгорбунская Н.А.
2. Осевая симметрия
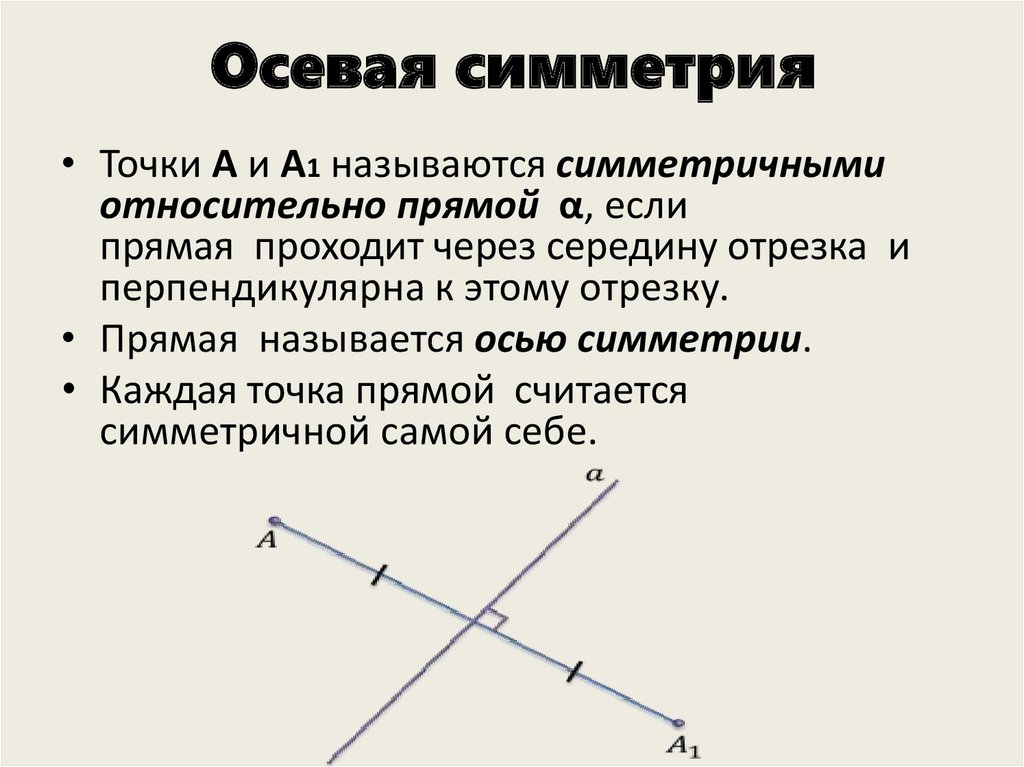
• Точки A и A1 называются симметричнымиотносительно прямой α, если
прямая проходит через середину отрезка и
перпендикулярна к этому отрезку.
• Прямая называется осью симметрии.
• Каждая точка прямой считается
симметричной самой себе.
3.
1) Оxyz — прямоугольная система координатZ
Оz — ось симметрии
2) М(x; y; z) и M1(x1; y1; z1),
симметричны относительно оси Оz
M1(x1; y1; z1)
М(x; y; z)
Формулы будут верны и в случае,
если точка М ⊂ Оz
O
Y
X
Осевая симметрия является движением
4.
Возникает вопрос, а если ось симметриисовпадает не с осью Оz, а, например, Оx
или Оy? Тогда связь между
координатами симметричных точек М и
М1 будет такая:
5. Задачи
1) Задача: найти координаты точек, в которые переходятточки A (0;1;2),B (3;-1;4), C (1;0;-2) при осевой симметрии
относительно координатных осей.
Решение: сначала найдём координаты точек в которые переходит
точки A, B, C при осевой симметрии относительно оси Ох.
Если точка M симметрична точке M1 относительно оси Ox то
x =x, y1=-y, z1=-z .
справедливы формулы: 1
A1 (0;-1;-2), B1 (3;1;-4), C1 (1;0;2).
Если точка M симметрична точке M1 относительно оси Oy то
справедливы формулы:
x1=-x, y1=y, z1=-z
A1 (0;1;-2), B1 (-3;1;-4), C1 (-1;0;2)
Если точка M симметрична точке M1 относительно оси Oz то
справедливы формулы:
x1=-x, y1=-y, z1=z
A1 (0;-1;2), B1 (-3;1;4), C1 (-1;0;-2)
6.
2) Задача:m
Доказать: при осевой симметрии прямая,
образующая с осью симметрии угол φ,
отображается на прямую, так же образующую с
осью симметрии угол φ
F
E
l
N
Решение:
φφ
A
при осевой симметрии прямая, образующая с осью
симметрии угол φ, отображается на прямую, так же
образующую с осью симметрии угол φ
a






 Математика
Математика








