Вычислительная физика. Лекция 4

1.

Лекция 4
Вычислительная физика

2.

План лекции
Численное интегрирование. Определенные
интегралы.
Метод
трапеций
Метод Симпсона
Численное интегрирование обыкновенных
дифференциальных уравнений. Задача Коши.
Схема
14.11.2019
Эйлера
Устойчивость схемы Эйлера
Обобщение на случай дифференциального
уравнения n-го порядка
Алгоритм Верле
Схемы
Рунге-Кутта
2-го
и 4-го порядков
Программирование
и информатика: Лекция
4
2

3.

Численное интегрированное
(определенные интегралы)
b
f ( x)dx
на [a, b],
f(x) - известная функция
a
Первообразная I Ф(x)
14.11.2019
Программирование и информатика: Лекция 4
b
a
10

4.

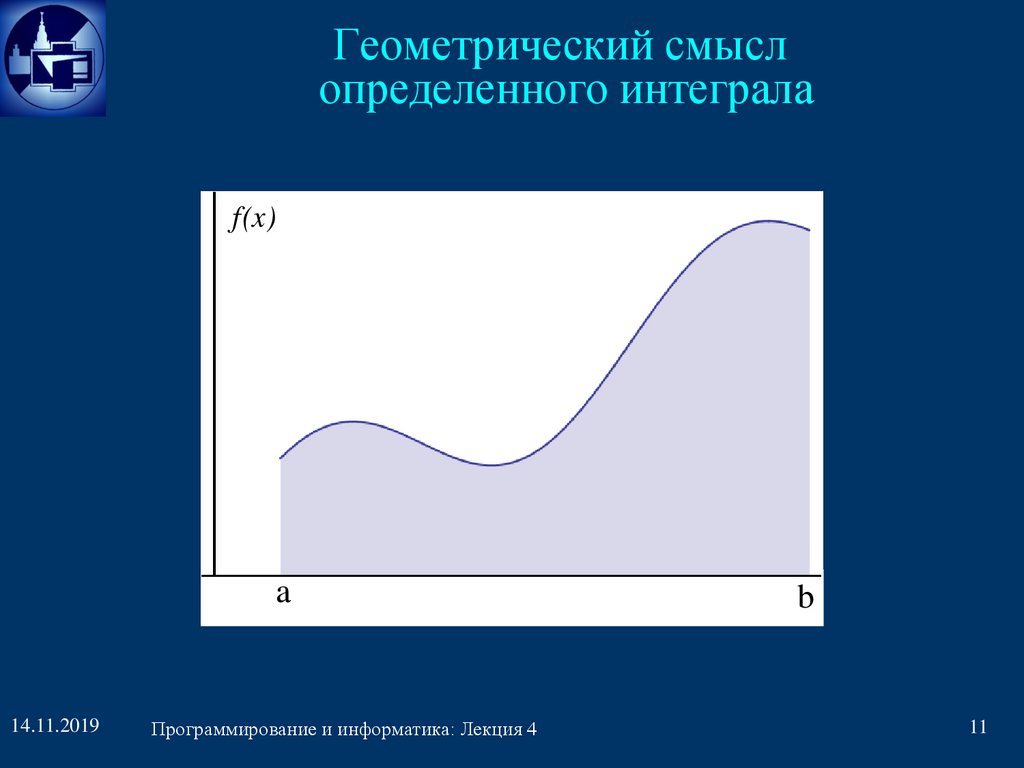
Геометрический смысл
определенного интеграла
f(x)
a
14.11.2019
Программирование и информатика: Лекция 4
b
11

5.

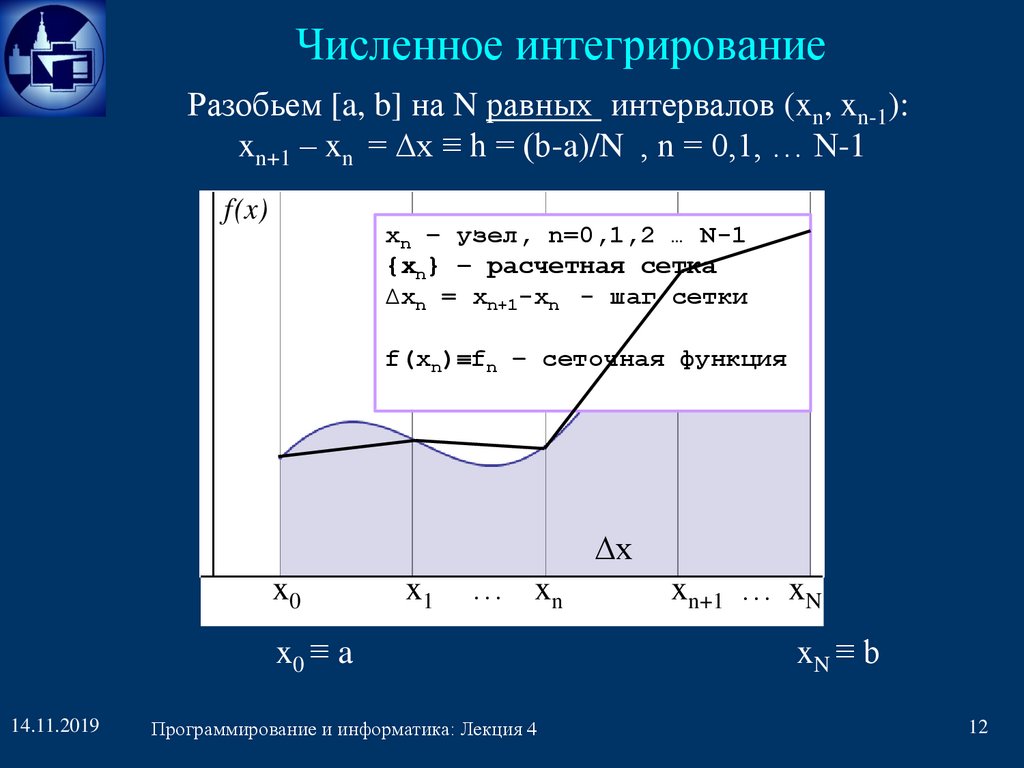
Численное интегрирование
Разобьем [a, b] на N равных интервалов (xn, xn-1):
xn+1 – xn = ∆x ≡ h = (b-a)/N , n = 0,1, … N-1
f(x)
xn – узел, n=0,1,2 … N-1
{xn} – расчетная сетка
∆xn = xn+1-xn - шаг сетки
f(xn) fn – сеточная функция
∆x
x0
x1
… xn
x0 ≡ a
14.11.2019
Программирование и информатика: Лекция 4
xn+1 … xN
xN ≡ b
12

6.

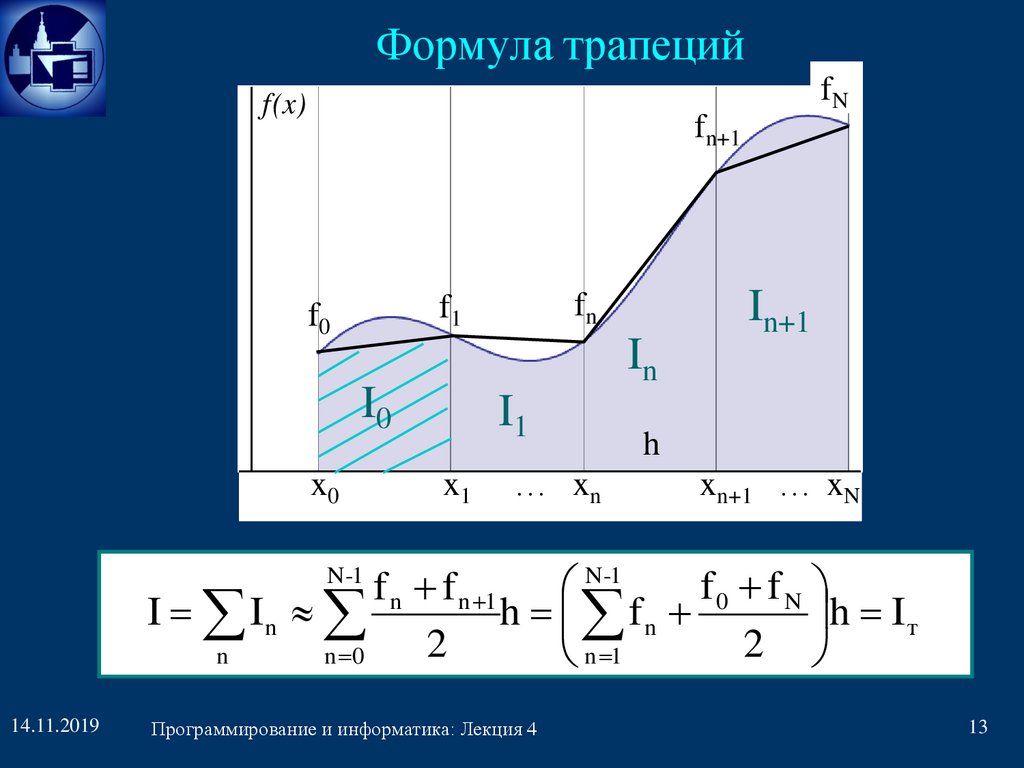
Формула трапеций
fN
f(x)
fn+1
fn
f1
f0
In
I0
x0
I1
x1
… xn
In+1
h
xn+1 … xN
f0 f N
f n f n 1
N-1
I In
h fn
h I т
2
2
n
n 0
n 1
N -1
14.11.2019
Программирование и информатика: Лекция 4
13

7.

Погрешность формулы трапеций
f0 f N
N-1
Iт fn
h
2
n 1
h2
I - I т (b a) max f ( x)
[a, b]
12
Погрешность ↓ как h2, если существует конечная f″(x)
Выбор шага интегрирования
Практический способ
14.11.2019
Программирование и информатика: Лекция 4
(2N)
I (N)
I
<
Т
Т
14

8.

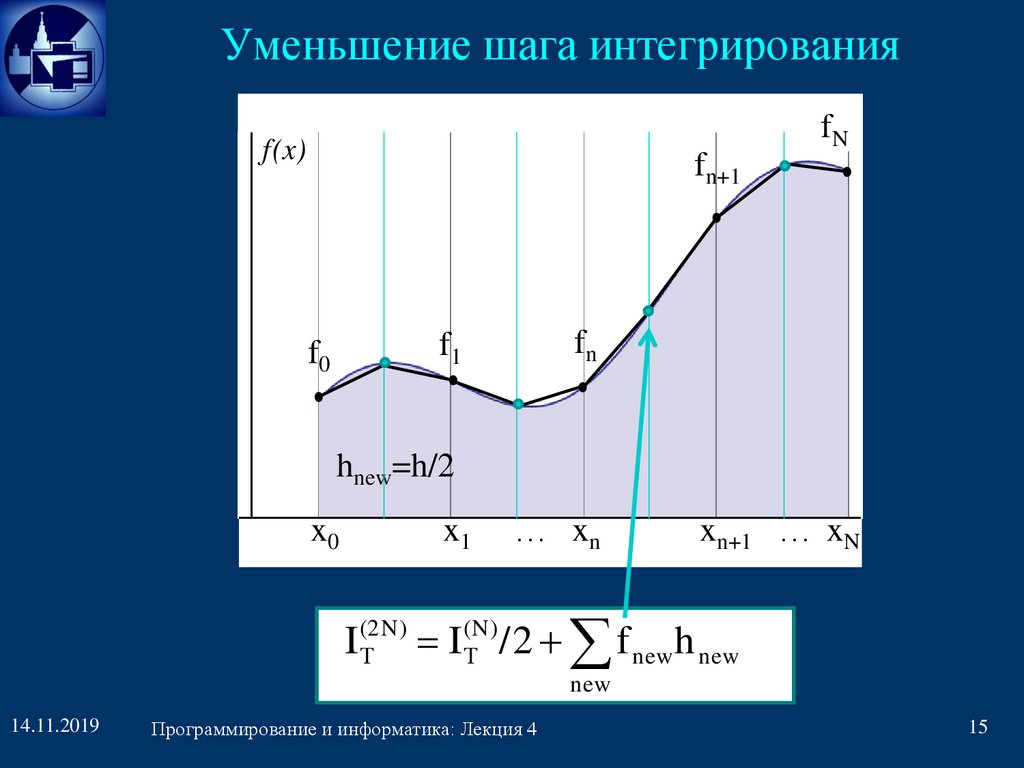
Уменьшение шага интегрирования
fN
f(x)
fn+1
fn
f1
f0
hnew=h/2
x0
x1
… xn
xn+1 … xN
(N)
I (2N)
I
Т
Т / 2 f new h new
new
14.11.2019
Программирование и информатика: Лекция 4
15

9.

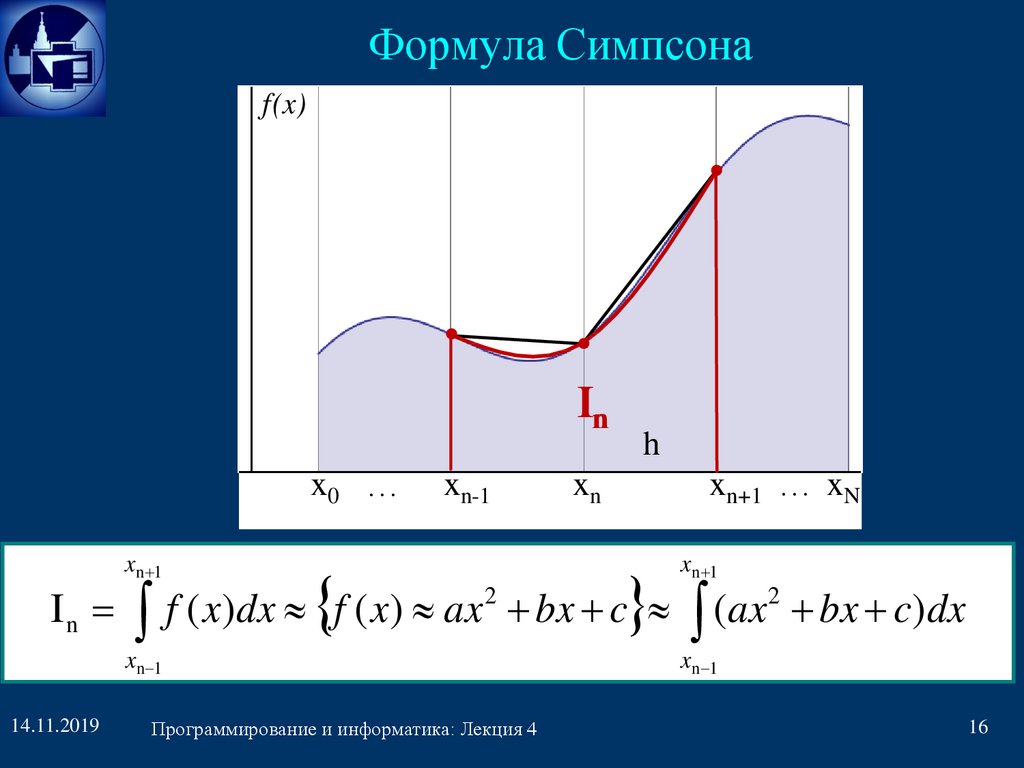
Формула Симпсона
f(x)
In
x0 …
In
xn 1
xn-1
xn+1 … xN
xn
Программирование и информатика: Лекция 4
xn 1
(ax
f ( x)dx f ( x) ax 2 bx c
xn 1
14.11.2019
h
2
bx c)dx
xn 1
16

10.

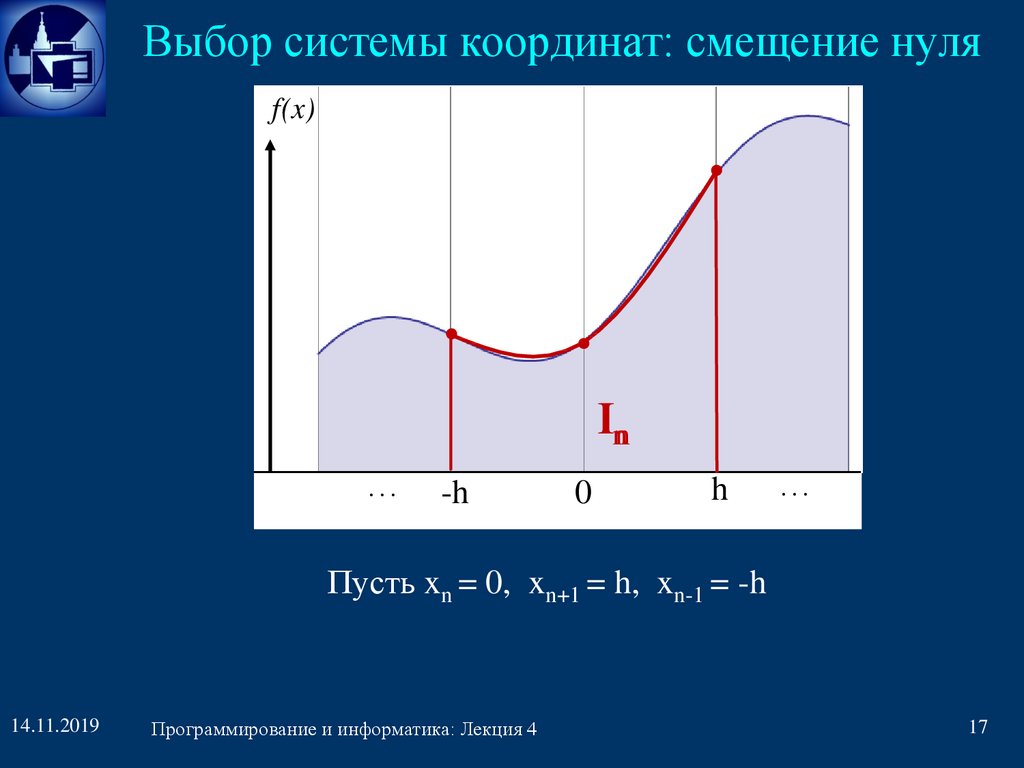
Выбор системы координат: смещение нуля
f(x)
In
…
-h
0
h
…
Пусть xn = 0, xn+1 = h, xn-1 = -h
14.11.2019
Программирование и информатика: Лекция 4
17

11.

Формула Симпсона
xn 1
ax
I n (ax bx c)dx
3
xn 1
3 h
2
-h
h
c x -h
2 3
ah 2ch
3
f ( x) ax bx c
2
f n -1 f ( h) ah2 bh c
c fn
f n f (0) c
f n 1 f n -1 2 f n
a
2h 2
f n 1 f ( h) ah2 bh c
14.11.2019
Программирование и информатика: Лекция 4
18

12.

Формула Симпсона
2 3
I n ah 2ch
3
c fn
f n 1 f n -1 2 f n
a
2h 2
f n 1
f n 1 f n 1 4
f n 1 4
f n h h
fn
3
3
3
3
3
14.11.2019
Программирование и информатика: Лекция 4
19

13.

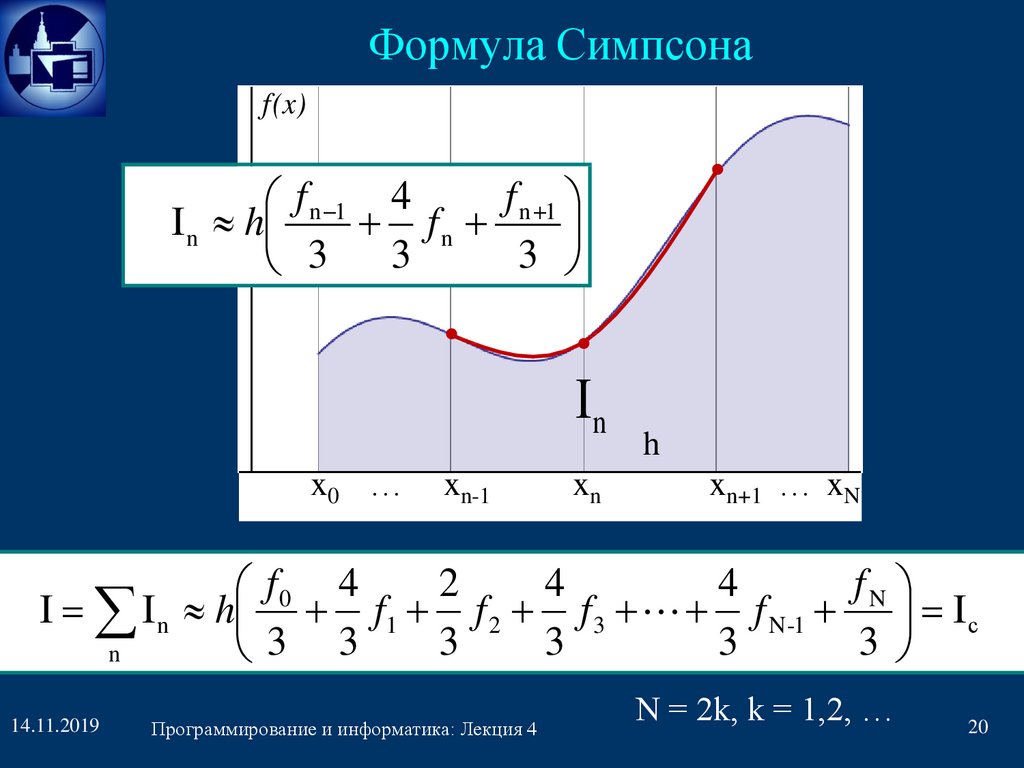
Формула Симпсона
f(x)
f n 1
f n 1 4
I n h
fn
3
3
3
In
x0 …
xn-1
xn
h
xn+1 … xN
fN
2
4
4
f0 4
I I n h f1 f 2 f 3 f N-1 I с
3
3
3
3
3 3
n
14.11.2019
Программирование и информатика: Лекция 4
N = 2k, k = 1,2, …
20

14.

Погрешность формулы Симпсона
fN
2
4
4
f0 4
I с h f1 f 2 f 3 f N-1
3
3
3
3
3 3
h4
(4)
I - Iс
(b a) max f ( x)
[a, b]
180
Погрешность ↓ как h4, если существует конечная f(4)(x)
14.11.2019
Программирование и информатика: Лекция 4
21

15.

Численное интегрирование обыкновенных
дифференциальных уравнений.
Задача Коши.
Уравнение первого порядка
du
f(u,t)
dt
u(t0 ) u 0
t0 t1 … tn tn+1 …
u – неизвестная функция
t – независимая переменная
Хотим знать решение на
отрезке [t0, tN]
tN t
tn – узел, n = 0,1,2 … N
{tn} – расчетная сетка
∆tn = tn+1-tn - шаг сетки
u(tn) un – сеточная функция
14.11.2019
Программирование и информатика: Лекция 4
22

16.

Схема Эйлера
du
f(u,t)
dt
u(t0 ) u 0
u n 1
t n 1
un
tn
du f(u,t)dt
un+1 - un = fn ∆t
14.11.2019
du f(u,t)dt
t0 t1 … tn tn+1 …
tN t
Аппроксимируем f на
[tn,tn+1] значением f(un, tn)
fn = const
un+1 = un + fn ∆t n = 0,1, …, N-1
Программирование и информатика: Лекция 4
23

17.

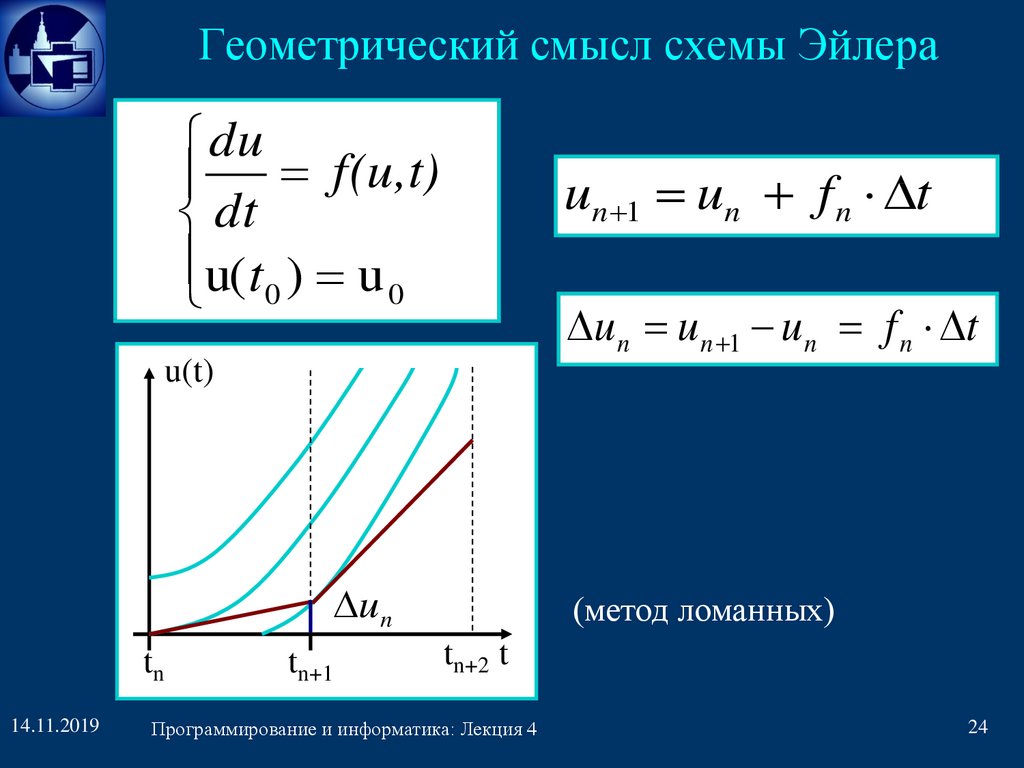
Геометрический смысл схемы Эйлера
du
f(u,t)
dt
u(t0 ) u 0
un 1 un f n t
u n u n 1 u n f n t
u(t)
u n
tn
14.11.2019
tn+1
(метод ломанных)
tn+2 t
Программирование и информатика: Лекция 4
24

18.

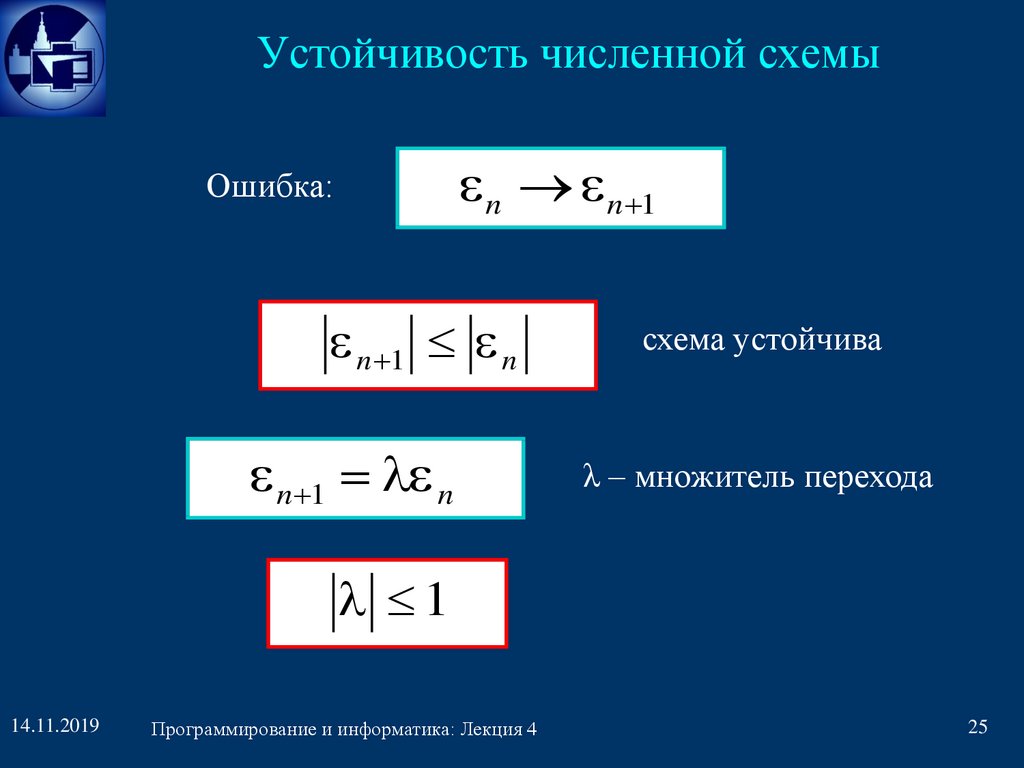
Устойчивость численной схемы
n n 1
Ошибка:
n 1 n
n 1 n
схема устойчива
λ – множитель перехода
1
14.11.2019
Программирование и информатика: Лекция 4
25

19.

Устойчивость схемы Эйлера
du
f(u,t)
dt
un 1 un f n t
u n 1 n 1 u n n f n (u n n ) t
Пусть на n-ом шаге ошибка εn, наdf
n+1 – εn+1,
f (u n
n )Эйлера
f (вuвиде:
n)
Запишем
схему
du
n O ( )
2
n
un
df
2
u n n f n (u n ) t
n t O ( n ) t
du
14.11.2019
Программирование и информатика: Лекция 4
26

20.

Множитель перехода для схемы Эйлера
n 1
n 1
n 1
df
2
n
n t O ( n ) t
du
df
n 1
t
du
df
n , 1
t
du
1 схема устойчива
14.11.2019
Программирование и информатика: Лекция 4
27

21.

Решение с нарастанием
df
0
du
u(t)
Схема неустойчива
для любого Δt !
t
df
1
t
du
14.11.2019
Программирование и информатика: Лекция 4
1
28

22.

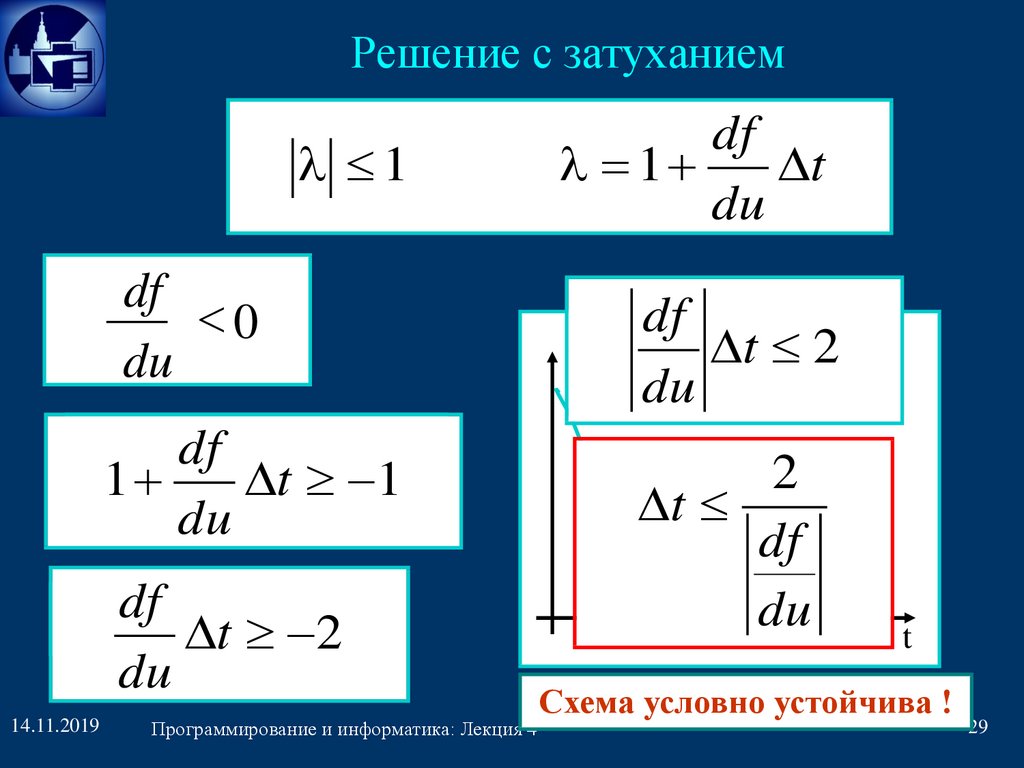
Решение с затуханием
1
df
<0
du
dfdf
11 t t 11
du
du
df1, t 21
du
14.11.2019
Программирование и информатика: Лекция 4
df
1
t
du
u(t)
df
t 2
du
2
t
df
du
t
Схема условно устойчива !
29

23.

Система уравнений
du1
f1(u1 , u2 ,t)
dt
du2 f (u , u ,t)
2 1
2
dt
u1 (t0 ) u10
u2 (t0 ) u20
Схема Эйлера
u1n 1 u1n f1 (u1n , u2 n , t n ) t u1n f1n t
u2 n 1 u2 n f 2 (u1n , u2 n , t n ) t u2 n f 2 n t
14.11.2019
Программирование и информатика: Лекция 4
30

24.

Векторный формализм
u u1 , u2
Пусть
f f1 , f 2
Задача Коши
du
f(u ,t)
dt
u (t0 ) u0
Численное решение по схеме Эйлера
un 1 un f n t
14.11.2019
Программирование и информатика: Лекция 4
31

25.

Обобщение на случай дифференциального
уравнения n-го порядка
Пусть n = 2
u f(u , u ,t) u (t0 ) u0 , u (t0 ) v 0
Замена
u v
dv
f(u, v,t)
dt
du v
dt
14.11.2019
тогда
u v
v(t 0 ) v 0
u (t 0 ) u 0
Программирование и информатика: Лекция 4
32

26.

Пример. Численное решение задачи
механики
Найти v(t), x(t)
x
Физическая модель: постоянная
сила тяжести, вязкое трение
v0
F kv
Закон Стокса
dx
v
2-ой закон Ньютона
dt
mx mg kx
d
v
k
v
x g 1
dt
mg
14.11.2019
Программирование и информатика: Лекция 4
33

27.

Скорость
m x mg kx
Предельная скорость
vt vt
0 mg kv t
mg
vt
k
dv
v
g 1
dt
vt
v(t 0) v 0
14.11.2019
Программирование и информатика: Лекция 4
a( v)
Задача Коши
34

28.

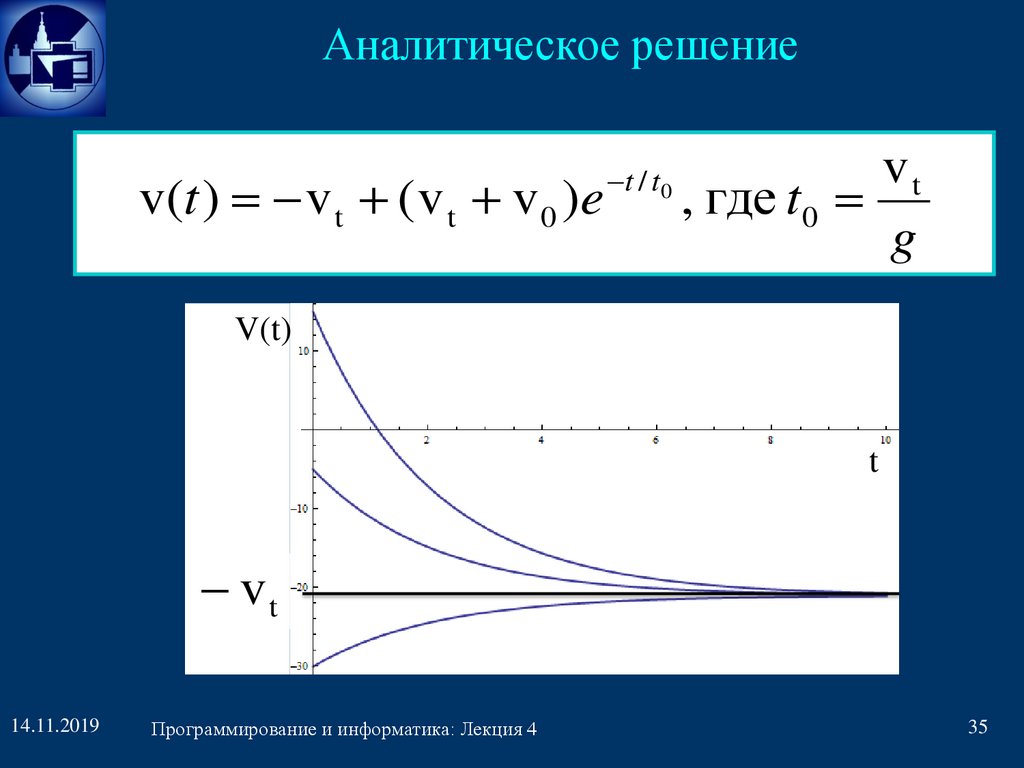
Аналитическое решение
v(t ) v t ( v t v 0 )e
t / t 0
vt
, где t0
g
V(t)
t
vt
14.11.2019
Программирование и информатика: Лекция 4
35

29.

Результаты из спорта
31м/c
25 м/c
20 м/c
25 м/c
16 м/c
9 м/c
14.11.2019
Программирование и информатика: Лекция 4
36

30.

Численное решение. Схема Эйлера
v n 1 v n an ( v n ,t n ) t
x n 1 x n v n t
v
x a g 1
vt
vn
an g 1
vt
14.11.2019
Устойчивость схемы
2v t
2
t
2t0
da
g
dv
Программирование и информатика: Лекция 4
37

31.

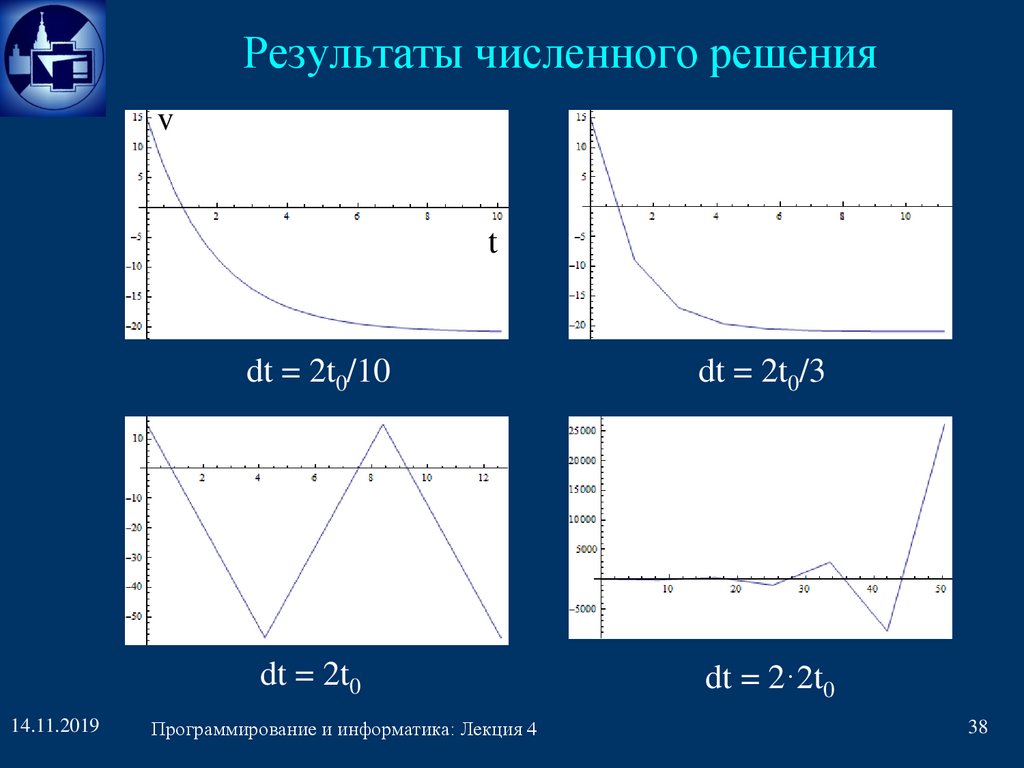
Результаты численного решения
v
t
14.11.2019
dt = 2t0/10
dt = 2t0/3
dt = 2t0
dt = 2·2t0
Программирование и информатика: Лекция 4
38

32.

Алгоритм Верле
Схема Эйлера
Самостартующий
алгоритм Верле
x n 1 x n v n t
x n 1
an
2
x n v n t
t
2
v n 1 v n a1n
1 t t ? ?
v n 1 v n (an an 1 ) t
2
14.11.2019
Программирование и информатика: Лекция 4
39

33.

Падение шарика в вязкой среде
v n 1
1
vn
(an an 1 ) t
2
vn
an g 1
vt
an 1
g v n
1
v n 1 v n
2
vt
14.11.2019
Программирование и информатика: Лекция 4
v n 1
g 1
vt
v n 1
1
t
v
t
40

34.

Явное выражение для алгоритма
v n 1
14.11.2019
vn
v n g 1
2v t
g
1
t
2v t
Программирование и информатика: Лекция 4
t
41

35.

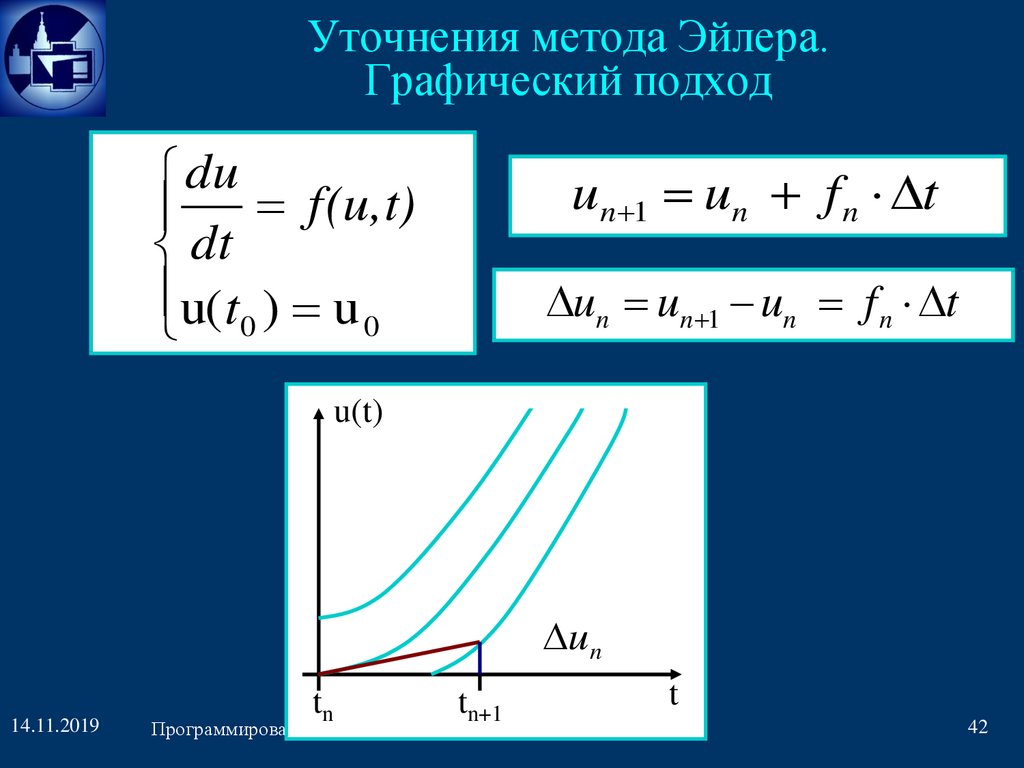
Уточнения метода Эйлера.
Графический подход
du
f(u,t)
dt
u(t0 ) u 0
un 1 un f n t
un un 1 un f n t
u(t)
u n
14.11.2019
tn
tn+1
Программирование и информатика: Лекция 4
t
42

36.

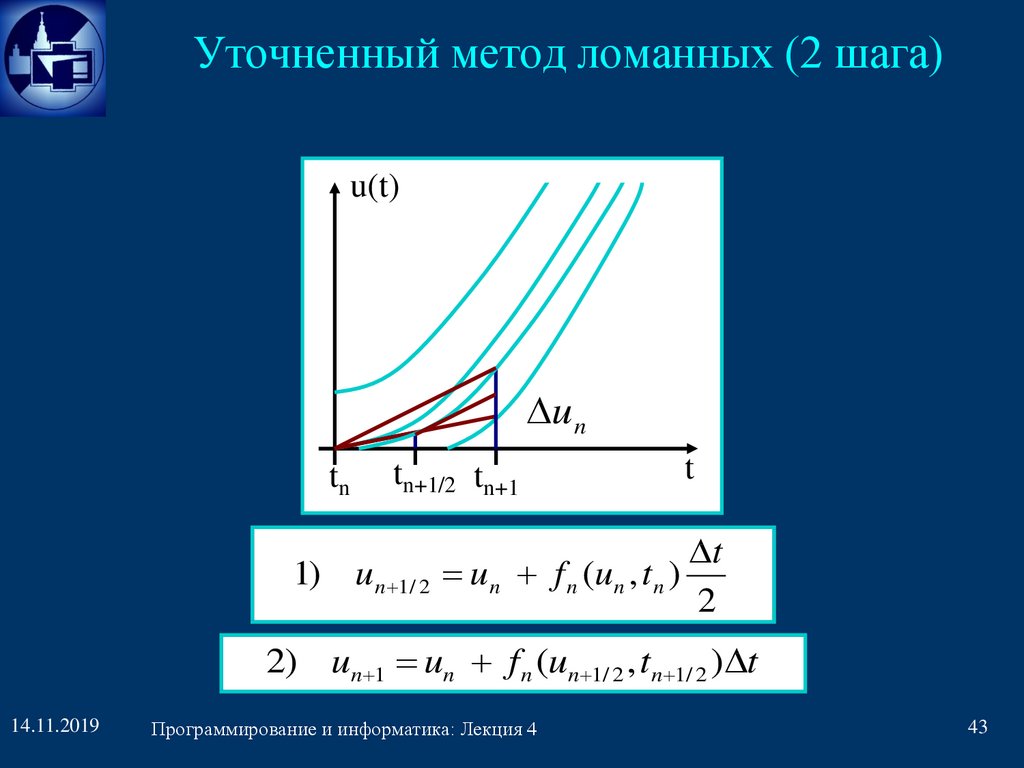
Уточненный метод ломанных (2 шага)
u(t)
u n
tn
tn+1/2 tn+1
1) un 1/ 2
t
t
u n f n (u n , t n )
2
2) un 1 un f n (un 1/ 2 , tn 1/ 2 ) t
14.11.2019
Программирование и информатика: Лекция 4
43

37.

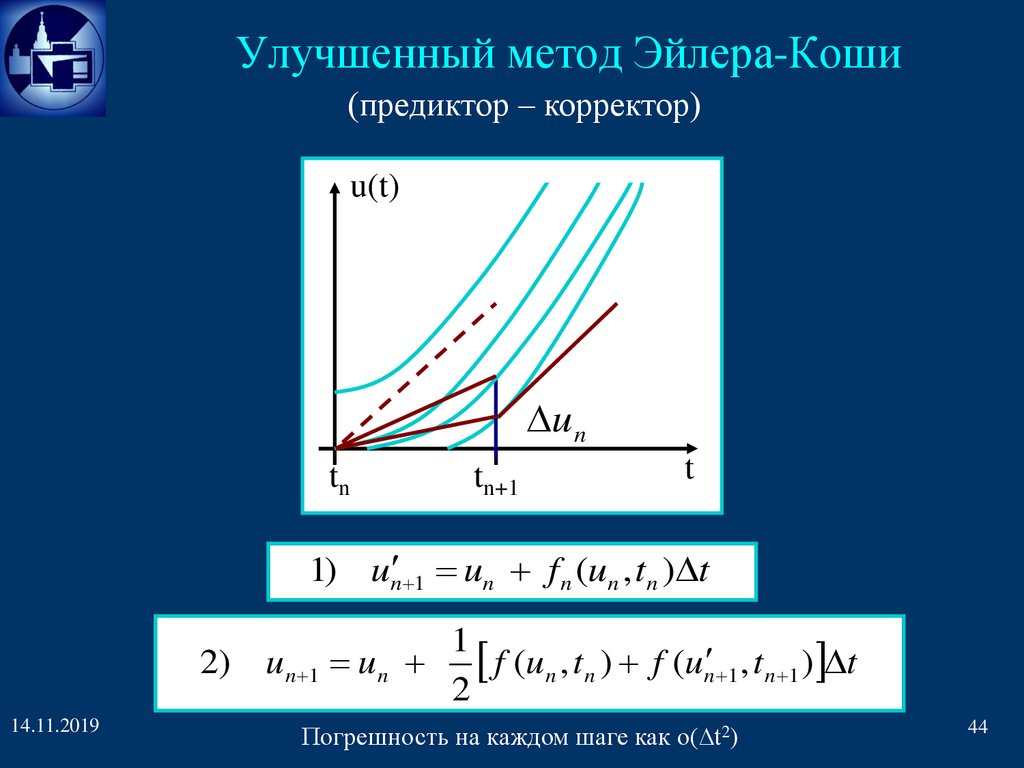
Улучшенный метод Эйлера-Коши
(предиктор – корректор)
u(t)
u n
tn
tn+1
t
1) un 1 un f n (un , tn ) t
2) u n 1
14.11.2019
1
u n f (u n , t n ) f (u n 1 , t n 1 ) t
2
Программирование
и информатика:на
Лекция
4
Погрешность
каждом
шаге как o(∆t2)
44

38.

Вывод формул численного интегрирования
du
f(u,t)
dt
du
d 2u t 2
u (t t ) u (t )
t 2
o( t 2 )
dt
dt 2
df t 2
2
u (t t ) u (t ) f (u, t ) t
o( t )
dt 2
df
f (u (t t ), t t ) f (u (t ), t )
O ( t )
dt
t
un 1
14.11.2019
t
un f n t f (un 1 , t n 1 ) f n o( t 2 )
2
Программирование и информатика: Лекция 4
45

39.

Вывод формул численного интегрирования
t
un 1 un f n t f (un 1 , t n 1 ) f n o( t 2 )
2
u n 1 u n f n t o( t )
u n 1
t
u n f (u n 1 , t n 1 ) f n
2
Улучшенная схема Эйлера-Коши!
14.11.2019
Программирование и информатика: Лекция 4
46

40.

Метод Рунге-Кутта 4-го порядка
du
f(u,t),
dt
u( t0 ) u 0
1
u n 1 u n (k1 2k 2 2k3 k 4 )
6
k1 f (u n , t n ) t
k1
t
k 2 f u n , t n t
2
2
k2
t
k3 f u n , t n t
2
2
k 4 f u n k3 , t n t t
14.11.2019
Программирование и информатика: Лекция 4
47

41.

Литература по лекционному
материалу
1. Н.Н. Калиткин. Численные методы. – BHV, 2011, 592 с.
14.11.2019
Программирование и информатика: Лекция 4
48