Modelling and Simulation IS 331. Lec (3)

1. IS 331

Faculty of Information Technology
Fall 2020
Modelling and Simulation
IS 331
Lec (3)
By Dr. Alaa Zaghloul

2. Simulation Examples

• Monte Carlo simulation
– Estimating π
– Craps (dice game)
• Time-stepped simulation
– Mortgage scenarios
• Trace-driven simulation
– Single-server queue (ssq1.c)
• Discrete-event simulation
– Witchcraft hair salon
2

3. Simulation Examples

• Monte Carlo simulation
–Estimating π
–Craps (dice game)
3

4. Example 3

Use the one-digit Random Number (6, 3, 5, 0, 8) to generate
random observations for :
a) Throwing an unbiased coin,
b) Throwing a die,
c) The color of a traffic found by a randomly arriving car
when it is green 40% of the time, yellow 10% of the time,
and red 50% of the time.

5. Example 3: Solution

(6, 3, 5, 0, 8)
a)To simulate a coin using one digit R.N.(0-9),
let 0 - 4 Represent a Head and
5 – 9 Represent a Tail;
so the solution will be:
R. Observations
(6, 3, 5, 0, 8)
(T, H, T, H, T)

6.

Example 3: Solution (6, 3, 5, 0, 8)
b) To simulate a die using number 0 – 9.
Let: 1 – 6 represents the faces of the die; then
0, 7, 8 and 9 are rejected.
So the solution will be
R. Observations
(6, 3, 5, 0, 8)
(6, 3, 5, reject, reject)

7.

Example 3: Solution (6, 3, 5, 0, 8)
c) Divide 0 – 9 into 3 classes according to the
given probability:
Green 40% 0, 1, 2, 3
Yellow 10%
4
Red
50% 5, 6, 7, 8, 9
R. Observations
So (6, 3, 5, 0, 8)
(Red, Green, Red ,Green, Red)

8. Example 4: A news boy

A news boy buys paper for 15 P.T.
each and sells them for 25 P.T. each. Unsold
papers have no value in analyzing past sells, it
is found that three demand distribution exist,
depending on news events in the papers. A
good interesting news day yield to many
potential customer, typical and poor days yield
to less interest. Historically 20% of days have
been “good”, 50% “typical”, 30% “Poor”, The
demand distributions are summarized :
Simulate 10 days period and determine main
daily profit, max profit, min profit if he decides
to buy 80 papers each day. Use the following
R.N :09 65 69 66 57 64 84 24 92 22
49 50 61 01 45 48 48 45 52 35
Demand
Types of new days
Good
Typical
Poor
40
0.05
50
0.20
0.03
60
0.41
0.07
70
0.26
0.28
80
0.08
0.30
0.02
90
0.25
0.15
100
0.07
0.28
110
0.24
120
0.12
130
0.09
140
0.06
150
0.04

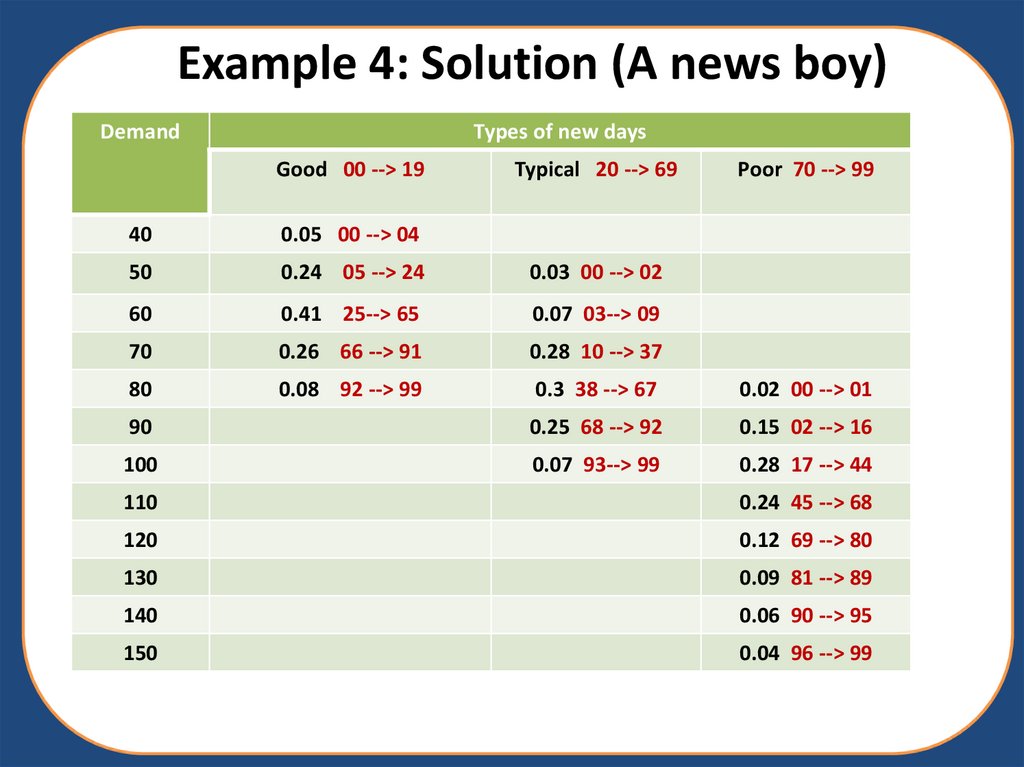
9. Example 4: Solution (A news boy)

Demand
Types of new days
Good 00 --> 19
Typical 20 --> 69
Poor 70 --> 99
40
0.05 00 --> 04
50
0.24 05 --> 24
0.03 00 --> 02
60
0.41 25--> 65
0.07 03--> 09
70
0.26 66 --> 91
0.28 10 --> 37
80
0.08 92 --> 99
0.3 38 --> 67
0.02 00 --> 01
90
0.25 68 --> 92
0.15 02 --> 16
100
0.07 93--> 99
0.28 17 --> 44
110
0.24 45 --> 68
120
0.12 69 --> 80
130
0.09 81 --> 89
140
0.06 90 --> 95
150
0.04 96 --> 99

10.

Example 4: Solution (A news boy)
Use the following R.N :09 65 69 66 57 64 84 24 92 22
49 50 61 01 45 48 48 45 52 35
1st Day:
RN 09 --> Good
RN 65 --> demand = 60
Profit = 60*25 – 80*15 = 300 P.T
2nd Day:
RN 69 --> Typical
RN 66 --> demand = 80
Profit = 80*25 – 80*15 = 800 P.T
3rd Day:
RN 57 --> Typical
RN 64 --> demand = 80
Profit = 80*25 – 80*15 = 800 P.T
4th Day:
RN 84 --> poor
RN 24 --> demand = 100
Profit = 80*25 – 80*15 = 800 P.T
; we calculate with demand 80 NOT
100 as the newsboy buy only 80 news paper each day.
08/01/2020

11.

Use the following R.N :09 65 69 66 57 64 84 24 92 22
49 50 61 01 45 48 48 45 52 35
5th Day:
RN 92 --> poor
RN 22 --> demand = 100
Profit = 80*25 – 80*15 =
6th Day:
RN 49 --> Typical
RN 50 --> demand = 80
Profit = 80*25 – 80*15 =
7th Day:
RN 61 --> Typical
RN 01 --> demand = 50
Profit = 50*25 – 80*15 =
8th Day:
RN 45 --> Typical
RN 48 --> demand = 80
Profit = 80*25 – 80*15 =
800 P.T
800 P.T
50 P.T
9th Day:
RN 48 --> Typical
RN 45 --> demand = 80
Profit = 80*25 – 80*15 = 800 P.T
10th Day:
RN 52 --> Typical
RN 35 --> demand = 70
Profit = 70*25 – 80*15 = 550 P.T
MIN profit: in 7th day which is 50 P.T
MAX profit: is 800 P.T
Main daily profit:
300+800+800+800+800+800+50+800+
800+550/10=650 PT
800 P.T
08/01/2020

12.

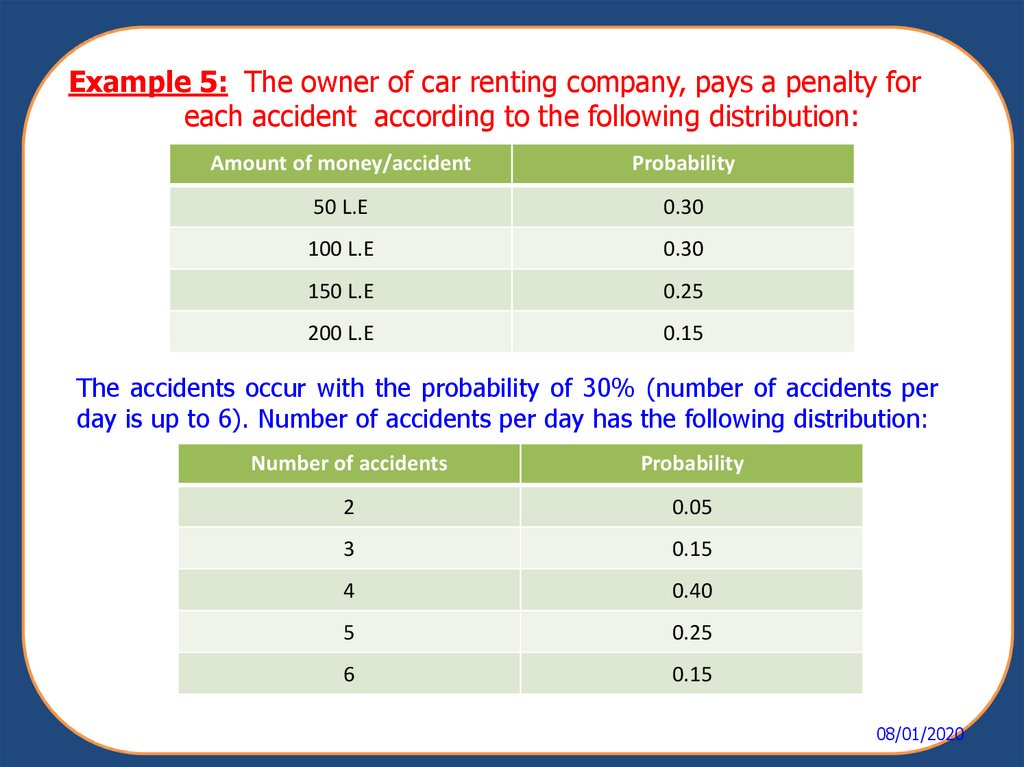
Example 5: The owner of car renting company, pays a penalty for
each accident according to the following distribution:
Amount of money/accident
Probability
50 L.E
0.30
100 L.E
0.30
150 L.E
0.25
200 L.E
0.15
The accidents occur with the probability of 30% (number of accidents per
day is up to 6). Number of accidents per day has the following distribution:
Number of accidents
Probability
2
0.05
3
0.15
4
0.40
5
0.25
6
0.15
08/01/2020

13.

Example 5: The owner of car renting company
Simulate 12 days. Based on your simulation what is the minimum
money the owner must have to cover the penalties occurred per
day.
Use the following R.N:
92 44 99 15 97 21 47 80 28 87 13 33 42 84 27 64
59 33 84 00 10 50 51 09 31 12 94 96 97 77

14.

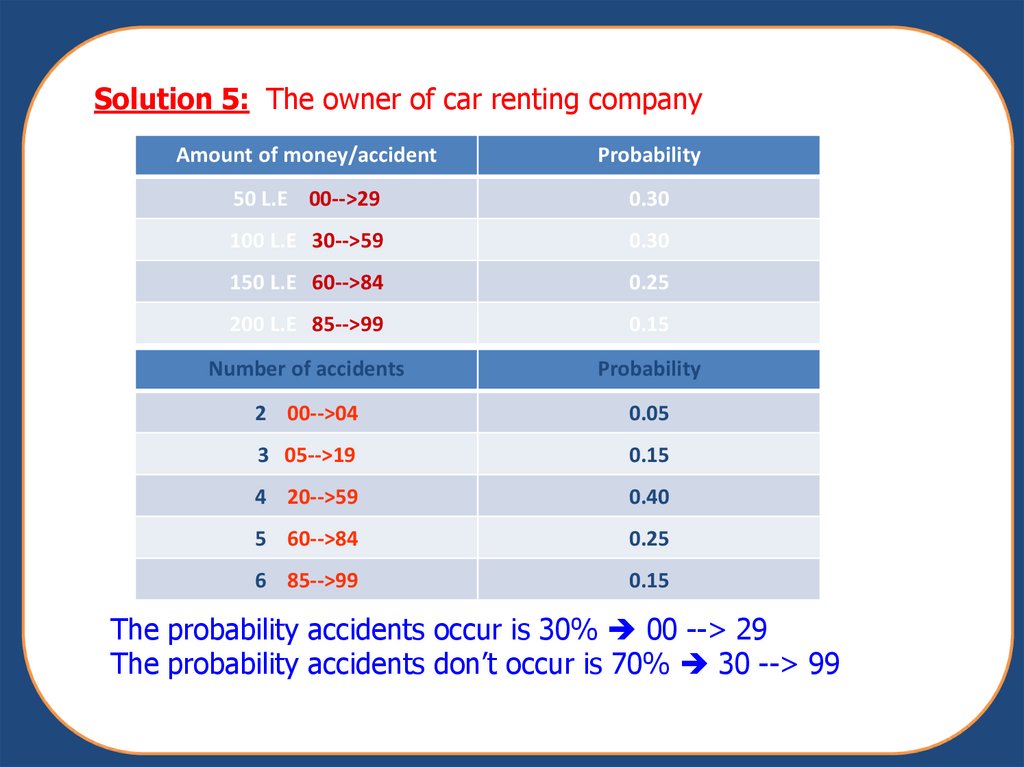
Solution 5: The owner of car renting company
Amount of money/accident
Probability
50 L.E 00-->29
0.30
100 L.E 30-->59
0.30
150 L.E 60-->84
0.25
200 L.E 85-->99
0.15
Number of accidents
Probability
2 00-->04
0.05
3 05-->19
0.15
4 20-->59
0.40
5 60-->84
0.25
6 85-->99
0.15
The probability accidents occur is 30% 00 --> 29
The probability accidents don’t occur is 70% 30 --> 99

15.

Solution 5: The owner of car renting company
Use the following R.N:
92 44 99 15 97 21 47 80 28
87 13 33 42 84 27 64
59 33 84 00 10 50 51 09 31
12 94 96 97 77
1st Day:
RN: 92 --> NO ACCIDENT
2ND Day:
RN: 44 --> NO ACCIDENT
3RD Day:
RN: 99 --> NO ACCIDENT
4TH Day:
RN: 15 --> ACCIDENT
RN: 97 --> Number of accidents = 6 accidents.
1th Accident:
RN: 21 --> Amount of money paid= 50 L.E
2ND Accident:
RN: 47 --> Amount of money paid= 100 L.E
3rd Accident:
RN: 80 --> Amount of money paid= 150 L.E
4th Accident:
RN: 28 --> Amount of money paid = 50 L.E
5th Accident:
RN: 87 --> Amount of money paid = 200 L.E
6th Accident:
RN: 13 --> Amount of money paid= 50 L.E
Then the total paid in this day = 50 + 100 + 150 + 50 + 200 + 50 = 600 L.E

16.

Solution 5: The owner of car renting company
Use the following R.N:
92 44 99 15 97 21 47 80 28
87 13 33 42 84 27 64
59 33 84 00 10 50 51 09 31
12 94 96 97 77
5th Day:
RN: 33 --> NO ACCIDENT
6TH Day:
RN: 42 --> NO ACCIDENT
7th Day:
RN: 84 --> NO ACCIDENT
8th Day:
RN: 27 --> ACCIDENT.
RN: 64 --> Number of accidents = 5 accidents.
1st Accident:
RN: 59 --> Amount of money paid = 100 L.E
2nd Accident:
RN: 33 --> Amount of money paid = 100 L.E
3rd Accident:
RN: 84 --> Amount of money paid = 150 L.E
4th Accident:
RN: 00 --> Amount of money paid = 50 L.E
5th Accident:
RN: 10 --> Amount of money paid = 50 L.E
Then the total paid in this day = 100 + 100 + 150 + 50 + 50 = 450 L.E

17.

Solution 5: The owner of car renting company
Use the following R.N:
92 44 99 15 97 21 47 80 28
87 13 33 42 84 27 64
59 33 84 00 10 50 51 09 31
12 94 96 97 77
9TH Day:
RN: 50 --> NO ACCIDENT.
10TH Day:
RN: 51 --> NO ACCIDENT.
11TH Day:
RN: 09 --> ACCIDENT.
RN: 31 --> Number of accidents = 4 accidents
1st Accident:
RN: 12 --> Amount of money paid= 50 L.E
2nd Accident:
RN: 94 --> Amount of money paid= 200 L.E
3rd Accident:
RN: 96 --> Amount of money paid= 200 L.E
4th Accident:
RN: 97 --> Amount of money paid= 200 L.E
Then the total paid in this day = 50 + 200 + 200 + 200 = 650 L.E
12th Day:
RN: 77 --> NO ACCIDENT
Based on the above simulation :- The minimum money the owner must have to cover
the penalties occurred per day (The maximum paid money in all days) = 650 L.E

18.

END