Прямые. Преобразование чертежа прямой. Две прямые

1. Прямые. Преобразование чертежа прямой. Две прямые.

Лекция № 2

2. План лекции

Взаимное положение точки и
прямой
2 Следы прямой
1
Способ перемены плоскостей
проекций
4 Преобразование чертежа
прямой
1 Взаимное положение двух
5
прямых
1 Проекции плоских углов
6
3

3.

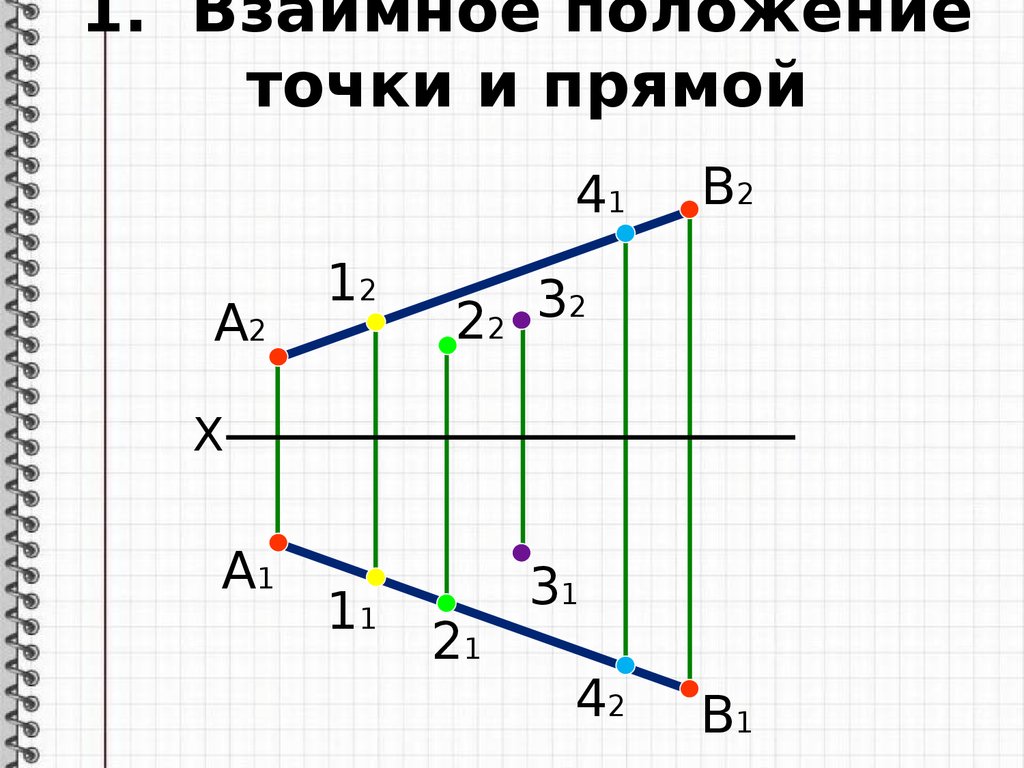
1. Взаимное положение
точки и прямой
41
А2
12
3
2
22
11
31
В2
X
А1
21
42
В1

4.

1.
Взаимное положение
точки и прямой
Если точка принадлежит прямой,
то проекции точки принадлежат
одноименным проекциям прямой
т.1 (AB) 11 (А1В1) 12 (А2В2)
т.2 (AB) 21 (А1В1) 22 (А2В2)
т.3 (AB) 31 (А1В1) 32 (А2В2)
т.4 (AB) 41 (А1В1) 42 (А2В2)

5.

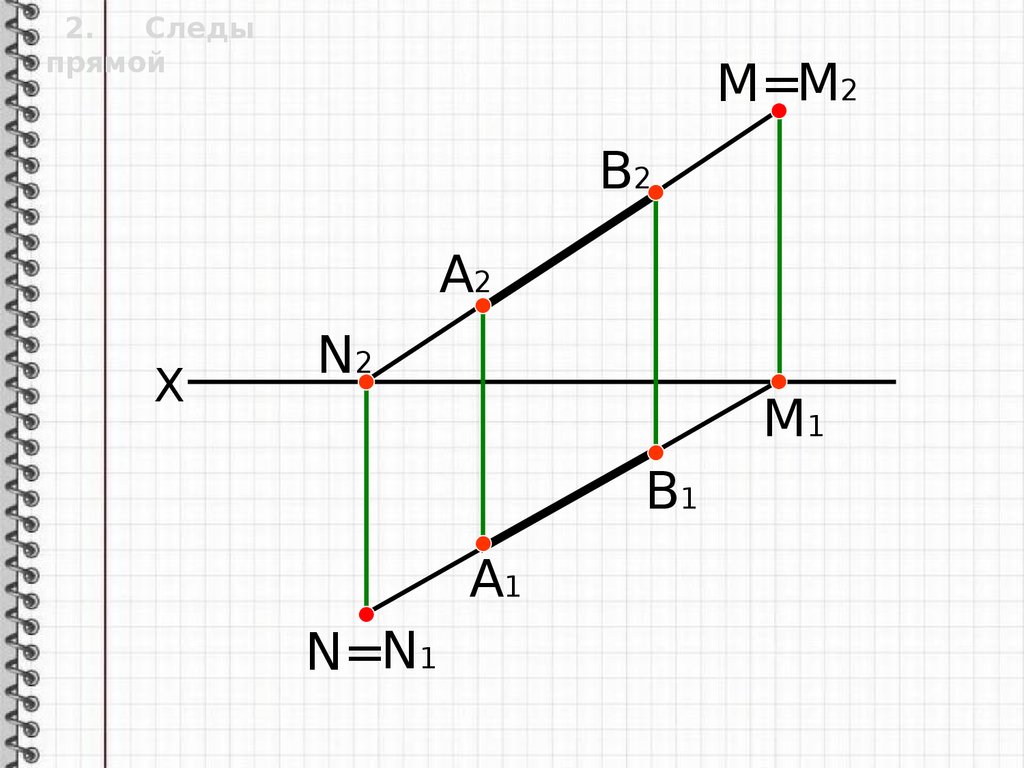
2.
прямой
Определение:
Следы
След прямой -
точка пересечения прямой
с плоскостью проекций.

6.

2.
Следы
прямой
П2
M=M2
В2
В
А2
X
N2
А
M1
А1
В1
N=N1
П1

7.

2.
Следы
прямой
M=M2
B2
А2
X
N2
M1
В1
А1
N=N1

8.

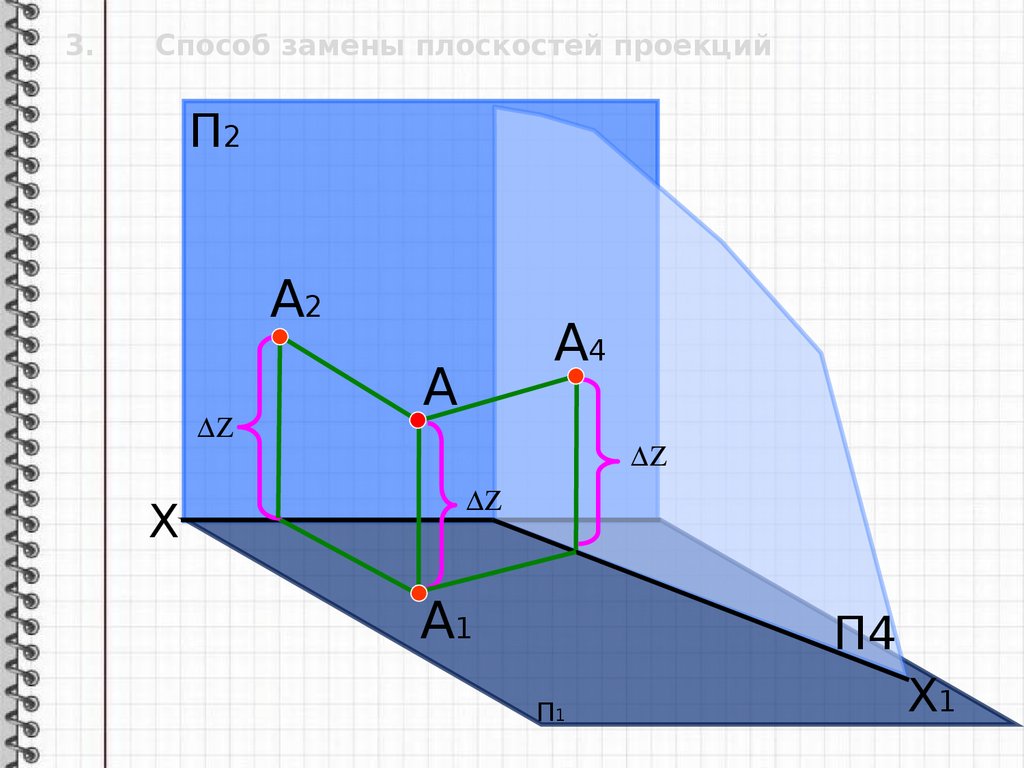
3. Способ замены
плоскостей проекций
Способ замены плоскостей
проекций заключается в
последовательной замене
одной из плоскостей проекций
на другую.
Геометрическая фигура своего
положения не меняет.

9.

3.
Способ замены плоскостей проекций
При этом должны быть
выдержаны следующие
условия:
1. Новая плоскость должна
быть перпендикулярна не
заменяемой плоскости проекций;
2. На новую плоскость
проекций геометрическая
фигура проецируется
ортогонально.

10.

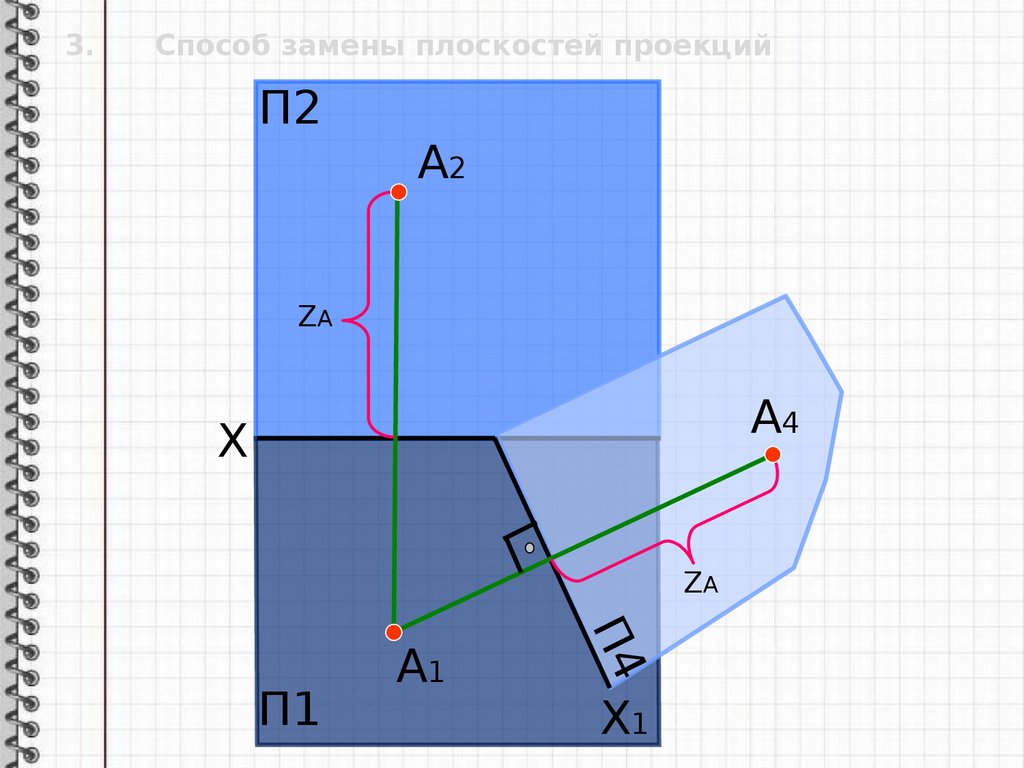
3.
Способ замены плоскостей проекций
П2
А2
X
А4
А
А1
П4
П1
Х1

11.

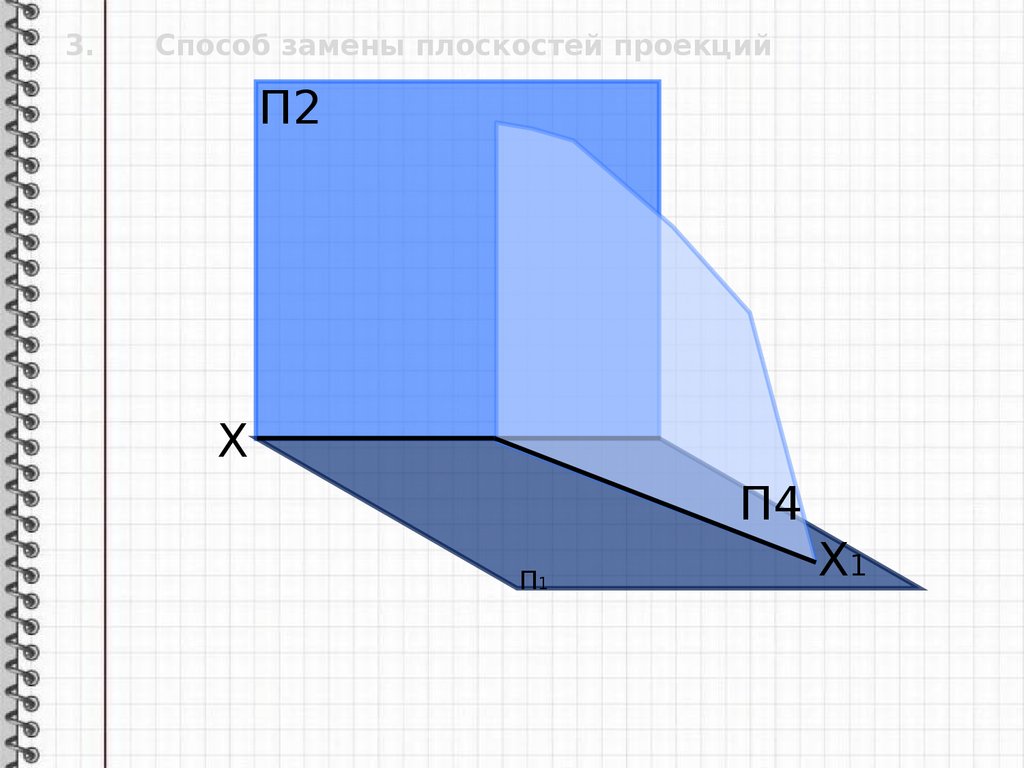
3.
Способ замены плоскостей проекций
П2
X
П4
П1
Х1

12.

3.
Способ замены плоскостей проекций
П2
X
П4
П1
Х1

13.

3.
Способ замены плоскостей проекций
П2
X
П4
П1
Х1

14.

3.
Способ замены плоскостей проекций
П2
А2
ZА
А4
X
ZА
П4
П1
А1
Х1

15.

3.
Способ замены плоскостей проекций
А2
ZА
А4
XП2
П1
ZА
П4
А1
Х1

16.

4.
Преобразование
чертежа прямой
Прямая общего положения
может быть преобразована
в:
1. прямую уровня;
2. проецирующую
прямую.

17.

4.
Преобразование чертежа прямой
Преобразование прямой общего положения в прямую уровня
П2
П1
П1
П4
В2
А2
П4 П1
ZВ
П4//(AB)
ZА
П
XП1
2
В1
А1
П1
Х1 П4
X1//(А1В1)
ZВ
ZА
А4
Н.В.
В4

18.

Преобразование чертежа прямой
Преобразование прямой уровня в проецирующую прямую
П2
П1
П1
П4
В2
А2
ZА= ZВ
П2
XП1
Н.
В.
В1
П4
А1
П4 П1
П4 AB
X1 А1В1
Х1 П1
4.
ZА= ZВ
А4=В4

19.

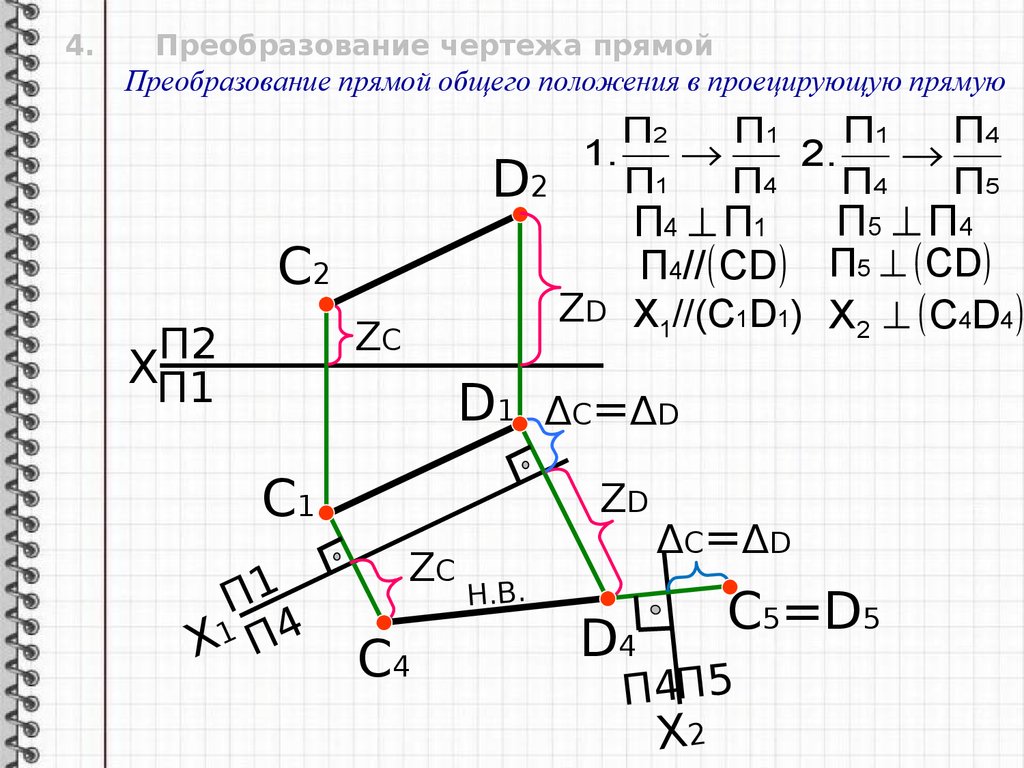
4.
Преобразование чертежа прямой
Преобразование прямой общего положения в проецирующую прямую
D2
С2
ZD
ZC
П2
XП1
D1
C1
П1
Х1 П4
П2
П1
П1
П4
1.
2.
П1
П4
П4
П5
П4 П1
П4// СD
П5 СD
X1//(C1D1) X 2 С4D4
ΔC= ΔD
ZD
ZC
C4
Н.В.
П5 П4
ΔC= ΔD
C5=D5
D4
П4П5
Х2

20.

5. Взаимное положение
двух прямых
Прямые в пространстве
могут быть:
• пересекающимися;
• скрещивающимися;
• параллельными
(в частности
совпадать).

21.

5.
Взаимное положение двух прямых
Пересекающиеся прямые
К2
X
К1
Если прямые в
пространстве
пересекаются,
то проекции
точки
пересечения
лежат на одной
линии связи.

22.

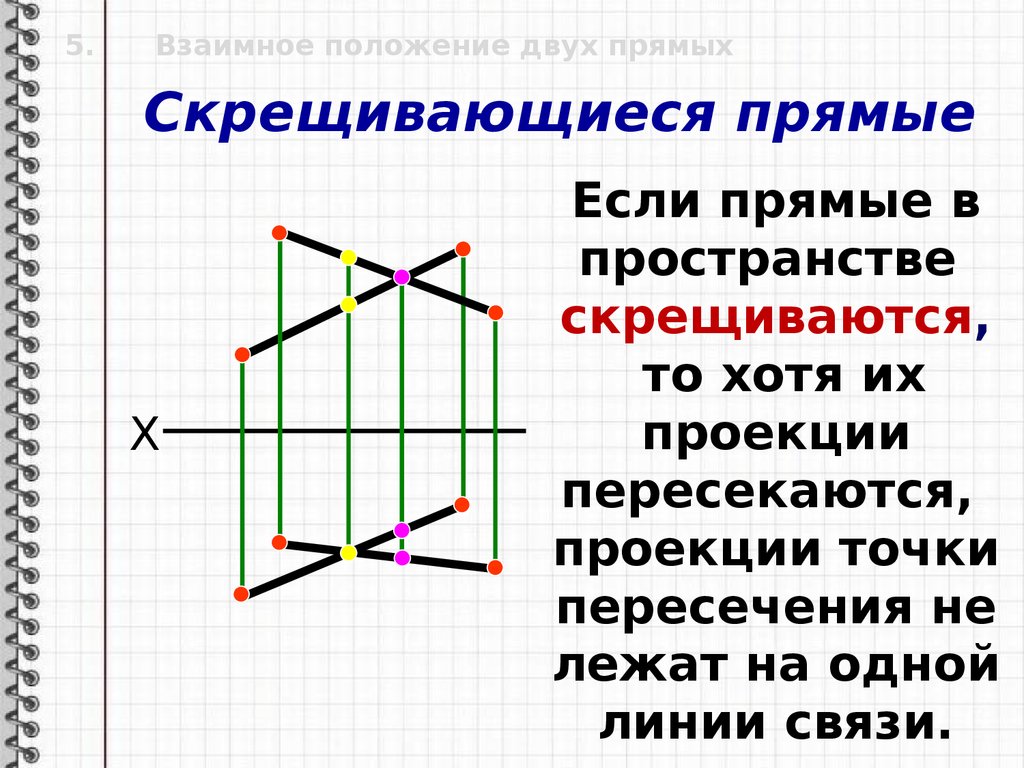
5.
Взаимное положение двух прямых
Скрещивающиеся прямые
X
Если прямые в
пространстве
скрещиваются,
то хотя их
проекции
пересекаются,
проекции точки
пересечения не
лежат на одной
линии связи.

23.

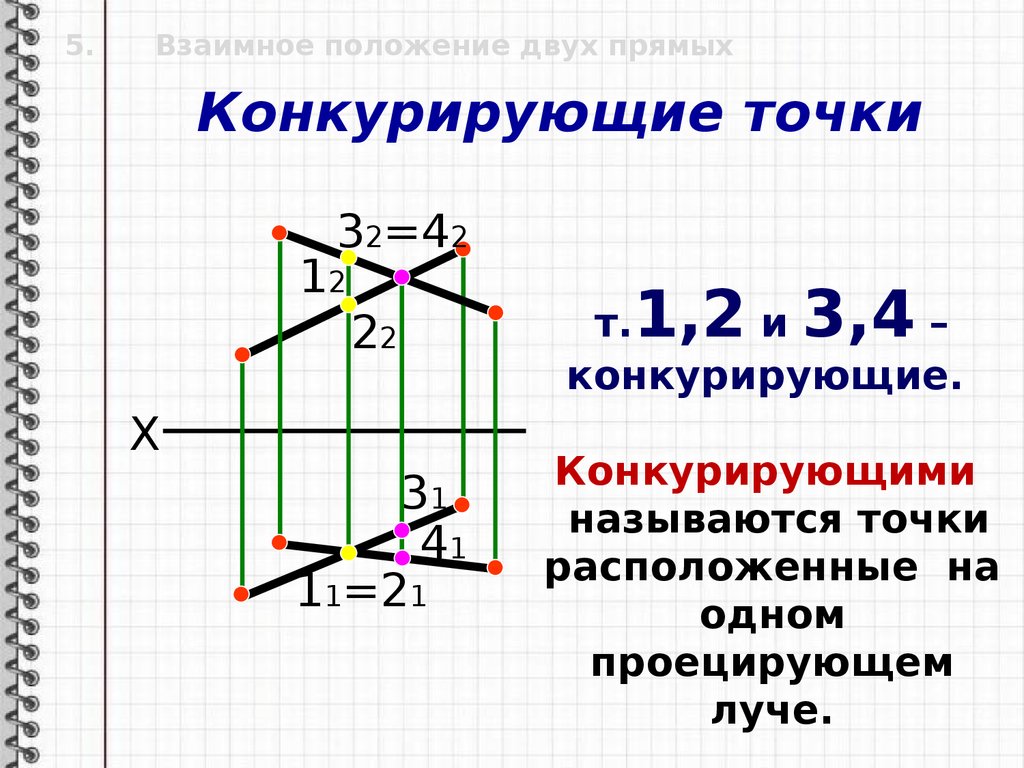
5.
Взаимное положение двух прямых
Конкурирующие точки
32=42
12
1,2 3,4
22
т.
и
–
конкурирующие.
31
41
11=21
Конкурирующими
называются точки
расположенные на
одном
проецирующем
луче.
X

24.

5.
Взаимное положение двух прямых
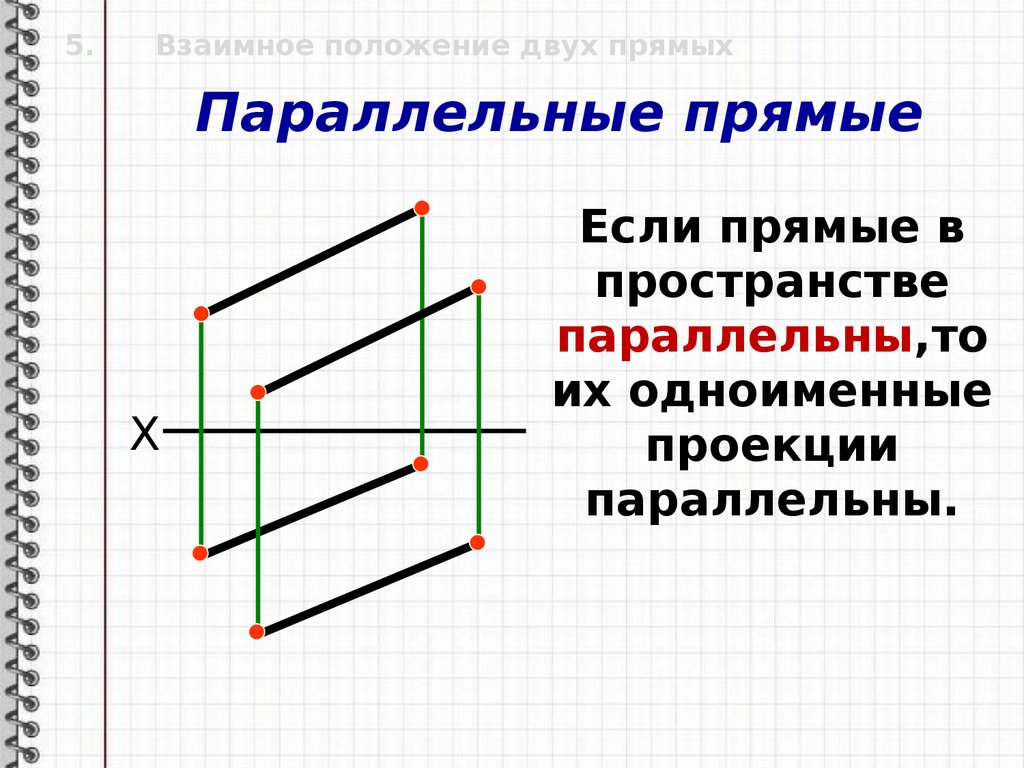
Параллельные прямые
X
Если прямые в
пространстве
параллельны,то
их одноименные
проекции
параллельны.

25.

5.
Взаимное положение двух прямых
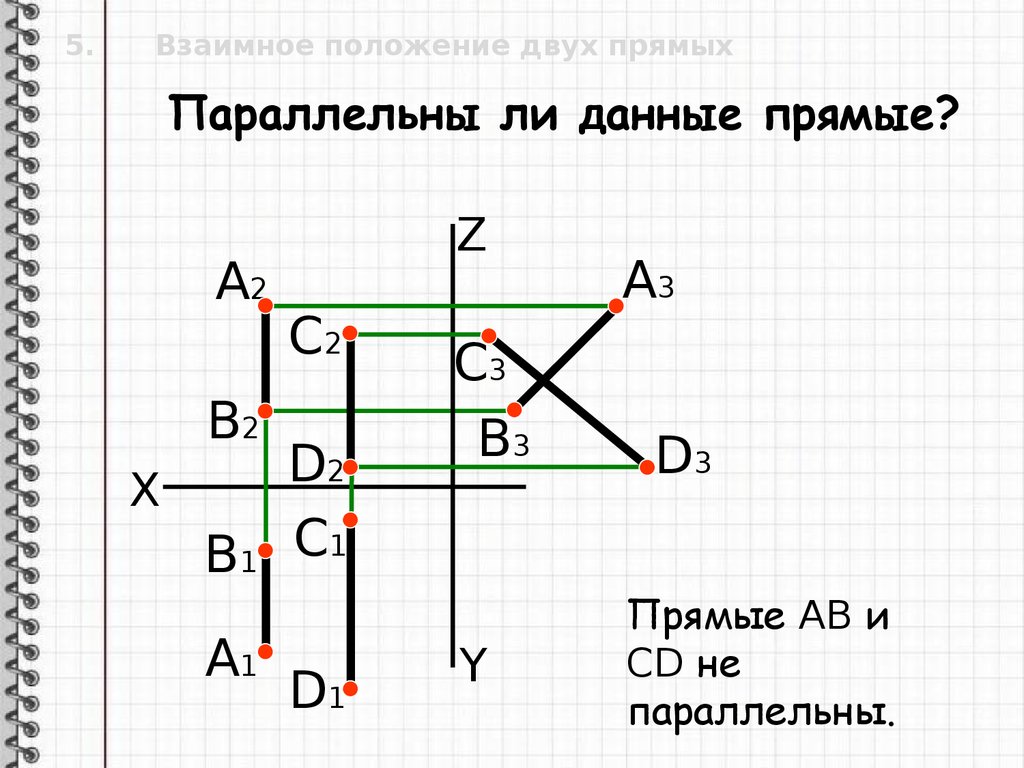
Параллельны ли данные прямые?
A2
Z
C2
B2
D
2
X
B1 C1
A1
D1
C3
B3
Y
A3
D3
Прямые AB и
CD не
параллельны.

26.

6.
Проекции
плоских углов
В зависимости от положения сторон
плоского угла по отношению к
плоскости проекций он может
проецироваться в угол от 0º до 180º.
Если стороны угла
параллельны плоскости,
то на эту плоскость угол
проецируется в
натуральную величину.

27.

6.
Проекции плоских углов.
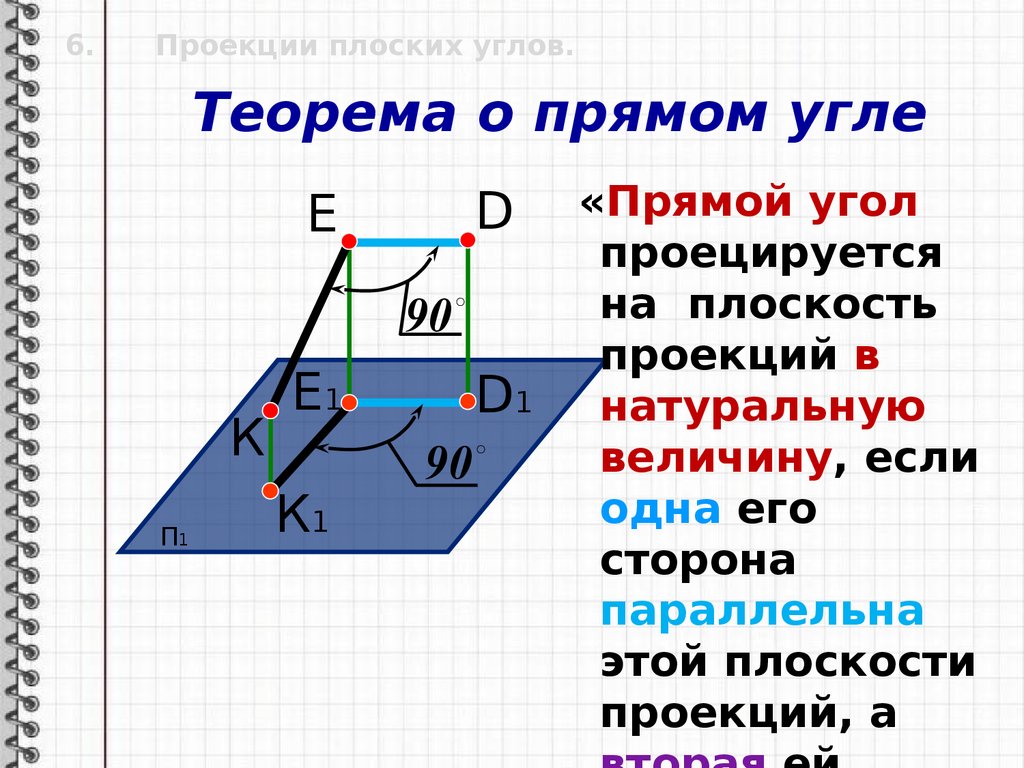
Теорема о прямом угле
D
Е
90
К
П1
Е1
К1
D1
90
«Прямой угол
проецируется
на плоскость
проекций в
натуральную
величину, если
одна его
сторона
параллельна
этой плоскости
проекций, а

28.

6.
Проекции плоских углов.
Теорема о прямом
угле
Дано (ED EK), (ED//П 1), (EK П 1)
:
К
1
Е
1
D
1
90
, т.е. (Е1D1) (Е1К1)
Доказат
ь:
ЕQ
D
90
К
П1
Е1
К1
D1
90
Доказательств
1. Qо:
: EK EЕ1 Q
2. ED EK , ED EЕ1
ED Q
3. Е1D1 // ED , ED Q
Е1D1 Q
4. Е1D1 E1К1
К1Е1D1 90

29.

Авторы:
доценты кафедры «Начертательная
геометрия, инженерная и компьютерная
графика» Омского Государственного
технического университета:
Бондарев Олег Александрович, к.т.н.,
Кайгородцева Наталья Викторовна,
к.пед.н.