Похожие презентации:
Long-period oscillations of sunspots and small-scale magnetic structures
1. Long-period oscillations of sunspots and small-scale magnetic structures
V.V. Smirnova2. Introduction
Solar oscillatory phenomenon has been observed in different solar structures (sunspots,pores (photosphere), coronal loops, faculae) by ground-based and cosmic instruments
(for example, see: Kobrin et al. 1976, Ofman 2000, Loukitcheva et al. 2005, Dorotovic
et al. 2008, Foullon et al. 2004, 2009, Yuan et al. 2011). A significant number of reports
have been devoted to short-period oscillations (3-5 minutes) of sunspots. These
oscillations are interpreted as the propagation of acoustic, slow or fast MHD waves
(Nakariakov 2007, Bogdan 2000, Bogdan et al. 2003, Parchevsky & Kosovichev 2009,
Felipe et al. 2010, Zhugzhda 2008).
Long quasi-periodic oscillations (30 minutes - several hours) of sunspots have been
studied considerably less than the 3-5 minutes oscillations (Efremov et al., 2015). The
mechanism responsible for the generation of such long periods in sunspots is under
discussion.
Long quasi-periodic oscillations with periods of 20-40, 60-100 minutes, were also
detected above sunspots at radio waves (microwave range, Gelfreikh et al. 2006,
Chorley et al. 2010, 2011; Abramov-Maximov et al. 2013, 2018, 2019).
The question is: what is the nature of long-period components in the oscillatory
spectrum of sunspots (and radio source above sunspots)?
3. Introduction
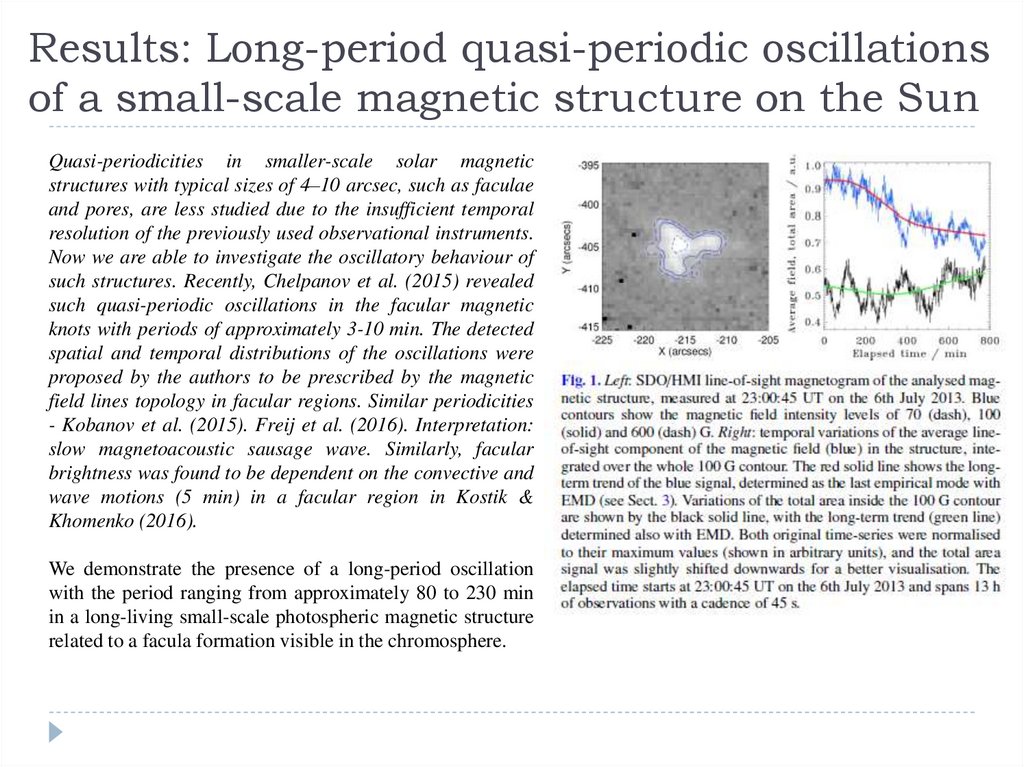
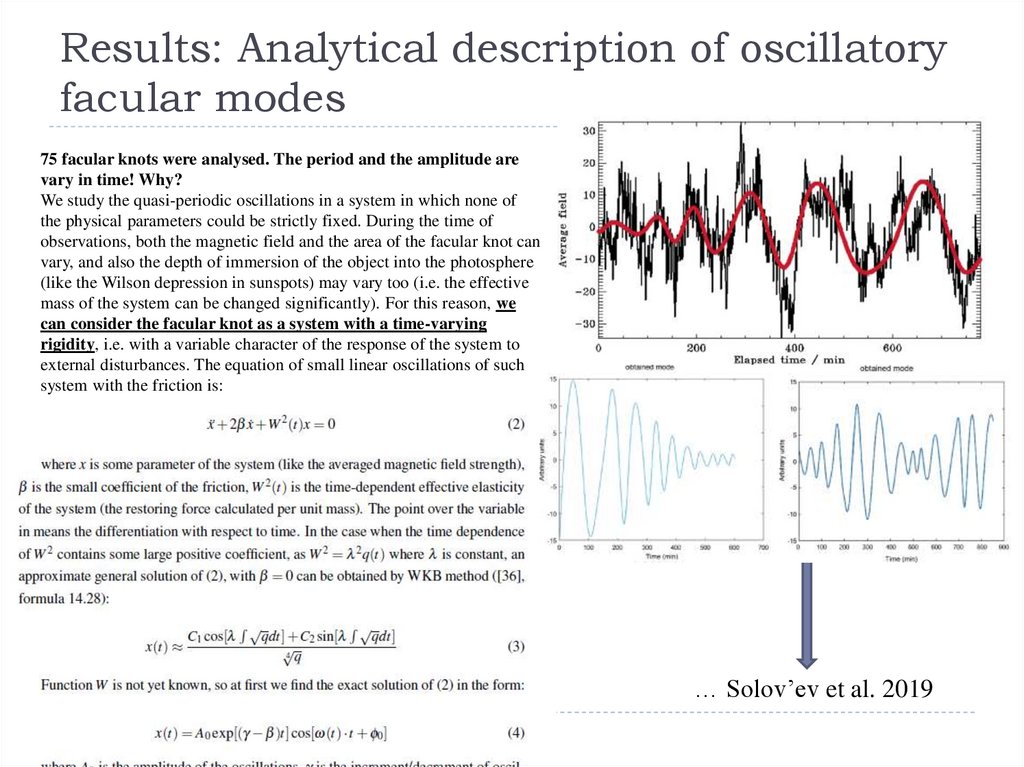
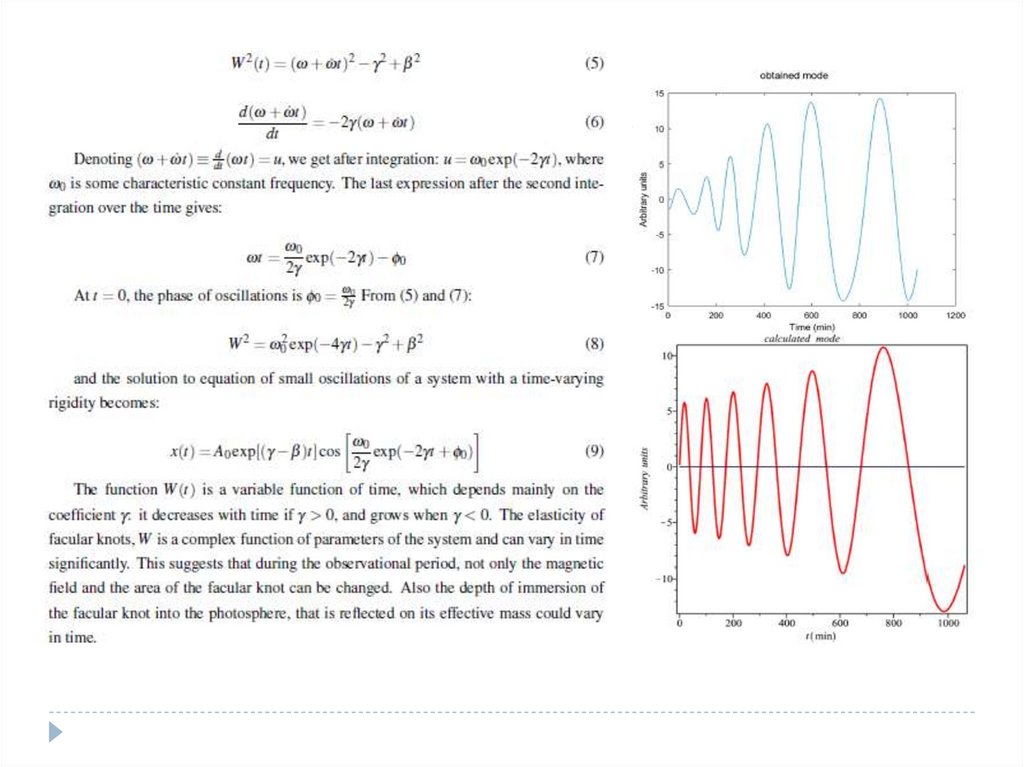
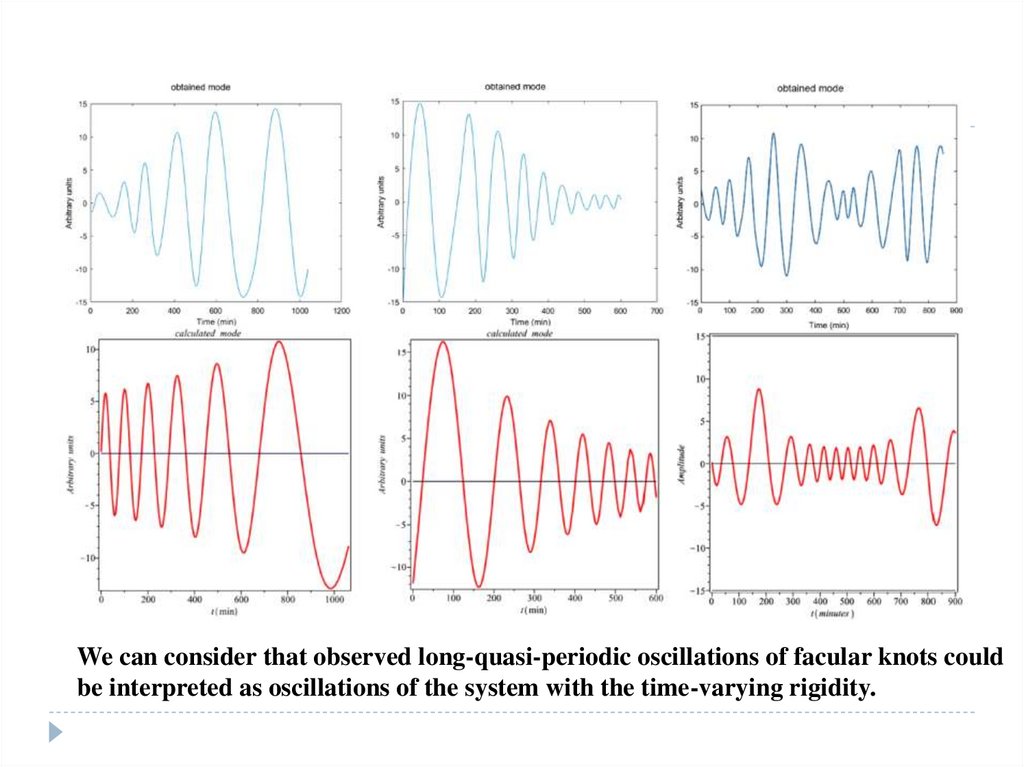
More interesting – long quasi-periodic oscillations of small-scale solar magneticstructures (facular knots). Recently proposed by Kolotkov et al. 2017 and Riehokainen
et al. 2019. Periods: 80-250 minutes. No analytical interpretation.
This study represents the results of: 1. the investigation of long quasi-periodic
oscillations of sunspots using observational data obtained at radio waves (ground-based
observations at 37 GHz) and data obtained from the observations of the line-of-sight
component of the magnetic field (Solar Dynamics Observatory (SDO) spacecraft); 2.
the investigation of long quasi-periodic oscillations of facular knots by using magnetic
field data, UV lines, continuum (SDO).
4. Goals
Based on the previous results, we decided to study long quasiperiodic oscillations of sunspots by using:radio observations obtained by Metsähovi radio telescope (14
meters antenna, 37 GHz, 2.4 arcmin, Finland) simultaneously
with the line-of-sight component of the magnetic field
(SDO/HMI);
study of long quasi-periodic oscillations of small-scale
magnetic structures by using:
line-of-sight component of the magnetic field (SDO/HMI);
UV and continuum intensity (SDO/AIA);
To provide the physical interpretation of the observed long
period oscillations of sunspots and small-scale magnetic
structures.
5. Instruments
We used data, obtained from the ground-based radio-telescope Metsähovi (14 metersantenna, 37 GHz; beam: 2.4 arc min., Metsähovi radio-observatory, Finland).
Solar Dynamics Observatory (SDO) data: line-of-sight component of the magnetic
field, and continuum data, provided by Helioseismic and Magnetic Imager (HMI)
(http://sdo.gsfc.nasa.gov/). It gives one-arc-second resolution full-disc images of
Doppler velocity and line-of-sight component of the magnetic field every 45
seconds (Scherrer et al. 2012); UV maps from the Atmospheric Imaging Assembly
instrument (AIA).
6. Results: Modulation of 37 GHz radio emission above sunspots
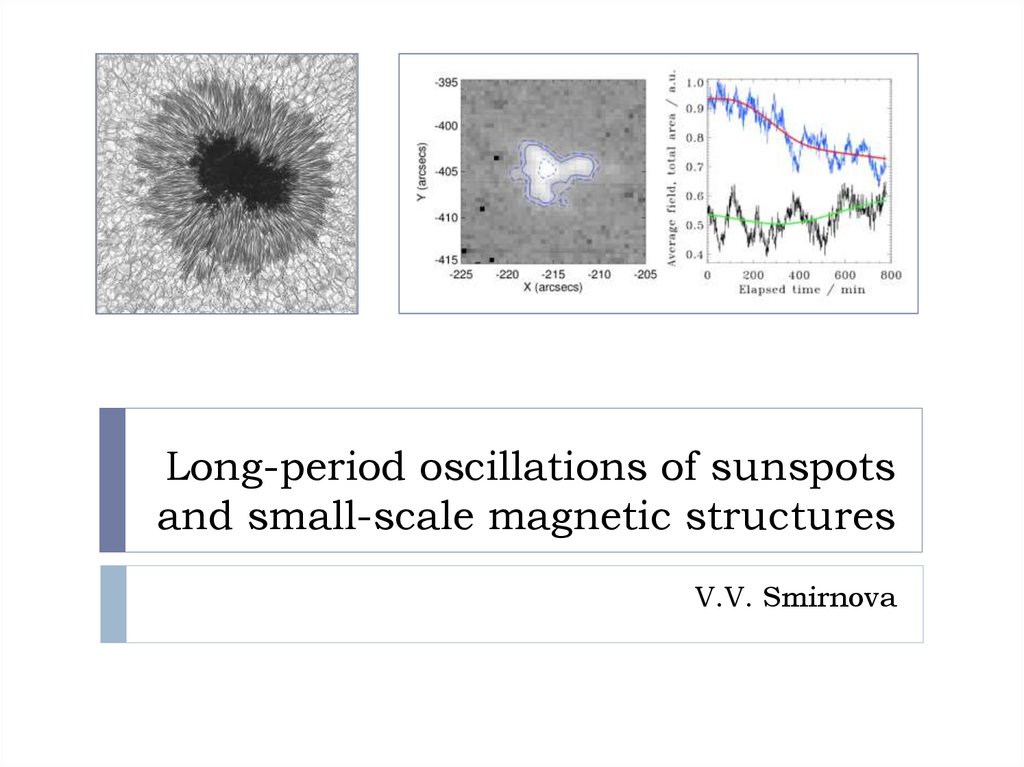
Using the wavelet analysis we found that periods of these long QPOs of 200–400 minutes (Smirnova et al. 2013, 2015). Also, we found time delays between
the studied time series: time variations of radio intensity were lagged in relation
to the time variations of the magnetic field in the sunspot. The values of the time
delays were estimated by the calculation of maximum correlation coefficient
between the corresponding time series for every active regions. Long-period
oscillations of sunspots were interpreted in accordance with “shallow” sunspot
model (Solov’ev and Kirichek 2008, 2009, 2014). In this model, the sunspot
oscillates along the vertical direction as a holistic stable magnetic structure near
the position of its equilibrium. One general physical process: RS oscillations
depends on the sunspot variations?
But the question is: how sunspot oscillations propagate to the chromosphere?
7.
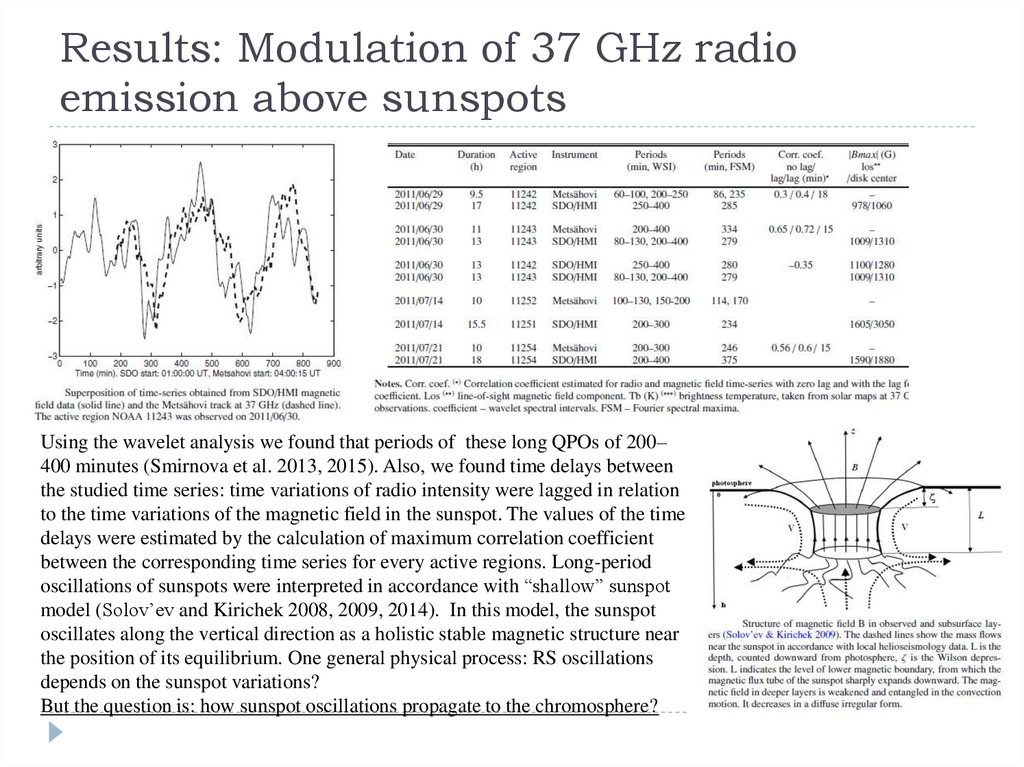
Usually, time delay effects observed in coronal loops with the length of about 50–300 Mm is interpreted as the time propagation ofAlfven waves (Roberts 2000; Nakariakov and Stepanov 2007). However, we should take into account that radio sources at 37 GHz
are located in chromosphere or transition region where plasma temperature is 10000 K in accordance with the model of the solar
atmosphere proposed by Avrett and Loeser (2008). For this reason, the typical length of the loops in our case should be shorter than
the lengths of coronal loops. Additionally, Alfven waves are incompressible and could not change the plasma density in the thermal
radio source to produce the observed variations of radio intensity. Thus, we should consider the time delay effect in our case as the
propagation of acoustic or slow magnetoacoustic waves. These waves could provide a relatively rapid relaxation of plasma of radio
source in accordance with slowly changing conditions at the lower boundary (photosphere). Considering that the slow magnetoacoustic waves propagate along the magnetic field with the same speed as the acoustic wave, we will use in further estimations is the
sound speed as the typical velocity of the propagation of disturbances from the sunspot to the radio source. Time-delays – two
methods: 1. linear Pearson correlation between the magnetic field and the radio intensity variations to get the cross correlation
coefficients as a function of time (Tcorr). 2: we can calculate the same time delay directly from the measurements of the distance
between the center of the radio source and the point at which the magnetic loop of radio source is originated. The brightness
distribution of the radio source has a sufficiently sharp maximum, therefore, the position of the radio maximum of the observed
source could be define sufficiently well.
8.
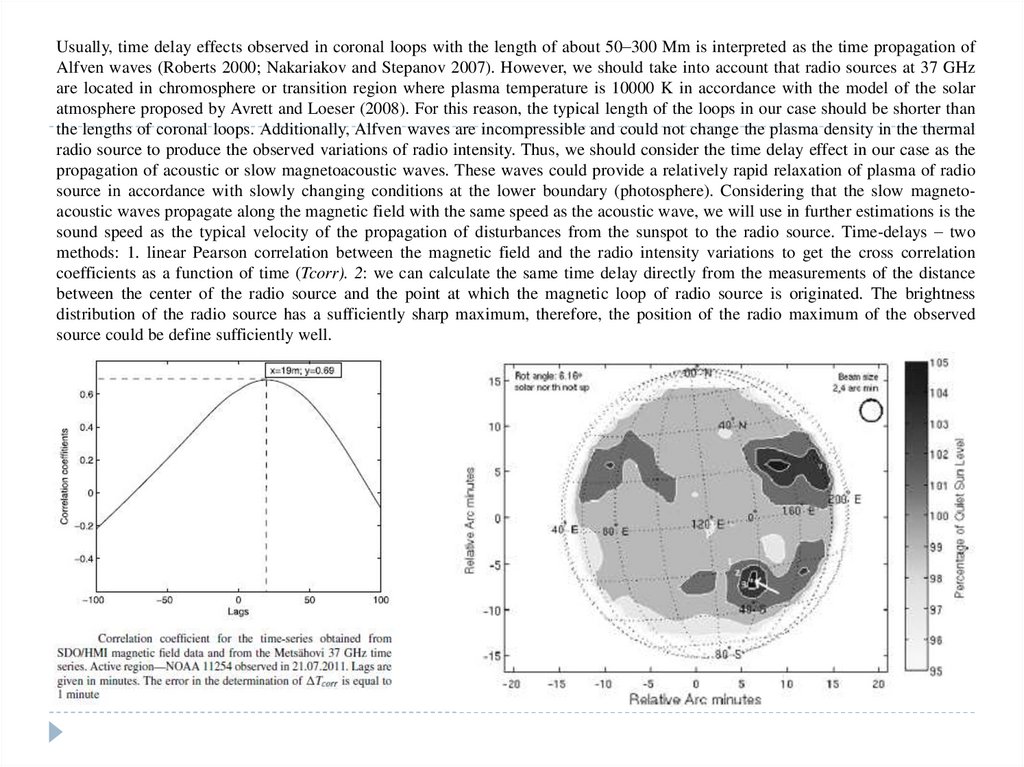
We assume the free-flux model that describes the formation of interspot radio sources. In this geometry, the half length of the magneticloop can be estimated as:
L =√l2 +h2,
where h is the height of the radio source at 37 GHz (8 mm) above the photosphere, l that is the distance between the projection of the
radio source maximum on the photosphere and the closest point of the sunspot penumbra. In accordance with the model of solar
atmosphere (Avrett and Loeser 2008) h ≈ 2000 km. In case of NOAA 11254, L = 16500 km. Now, we can derive the time delays as a time
propagation of the acoustic disturbances from the sunspot to the radio source:
where cs =













 Физика
Физика








