Понятие квадратного корня из неотрицательного числа

1. Тема урока: «Понятие квадратного корня из неотрицательного числа»

Цель урока:
дать понятие о корне из числа
научить находить а b по
определению

2. Понятие квадратного корня из неотрицательного числа

Задачи урока:
Ввести понятие квадратного корня их неотрицательного числа а и определение
арифметического квадратного корня из числа а.
Закрепить эти понятия в ходе выполнения упражнений.
Рассмотреть правила вычисления квадратного корня из неотрицательного числа.
Формировать умение вычислять квадратный корень из чисел и выражений.
Развивать логическое мышление учащихся.
Вырабатывать навыки устного вычисления.

3. Понятие квадратного корня из неотрицательного числа

1.
2.
3.
4.
5.
6.
План урока:
Организационный момент
Актуализация опорных знаний учащихся
Объяснение нового материала
Закрепление нового материала
Итог урока
Домашнее задание

4. Актуализация опорных знаний

№1. Вычислить:
а а а
( 3) 2
х х а а
0,7
( х а) ( х а)
( 2)
2
2
( 2)
3
20
3
2

5. Актуализация опорных знаний

№2. Найти значение х 2 при
1
х = 3; х = 4; х = - 5; х = 0; х = 2 ; х = - 4 .
№3. Решить уравнение:
х2 4
х
2
у
2
1
9
49
у
2
64
х
2
25
х
2
0

6.

Понятие квадратного корня из
неотрицательного числа
S KB 49 см
2
Какова сторона квадрата ?
Воспользуемся формулой
2
S a
2
49 a
а 7
a
Ответ:
a
a 7 см
S 7 49
2

7.

Понятие квадратного корня из
неотрицательного числа
Определение Арифметическим квадратным корнем
из числа а называется неотрицательное число,
квадрат которого равен а.
Это число обозначают
а
, число а - подкоренное выражение
Пример : так как 02 =0, то 0=0
22 =4, то 4=2
12 =1, то 1=1

8. Понятие квадратного корня из неотрицательного числа

а b является верным, если
1)
b 0 2)
b2 a
Равенство
При а<0 выражение а не имеет смысла, так как
квадрат любого числа или положителен, или равен
нулю.
Например, не имеет смысла выражение
25

9. Понятие квадратного корня из неотрицательного числа

Операцию нахождения квадратного корня из
неотрицательного
числа
называют
извлечением квадратного корня.
Эта операция является обратной по
отношению к возведению в квадрат.
5 25
2
и
25 5

10. Понятие квадратного корня из неотрицательного числа

О знаке радикала
В записи а знак
называют
знаком радикала (от латинского
«Radix» - корень)

11. Понятие квадратного корня из неотрицательного числа

Устно:
Вычислить:
ЗАДАНИЕ
№ 298
№ 299
№ 300
№ 301
√
√
√
√

12. Понятие квадратного корня из неотрицательного числа

Вычислить:
№ 305 (а, б, в, г) √
Работа по таблице квадратов.
Устно:
№ 306
√

13. Понятие квадратного корня из неотрицательного числа

Из определения арифметического
квадратного корня следует, что при любом а,
при котором выражение а имеет смысл,
верно равенство
а
Задание:
Вычислить № 309
2
√
а

14. Понятие квадратного корня из неотрицательного числа

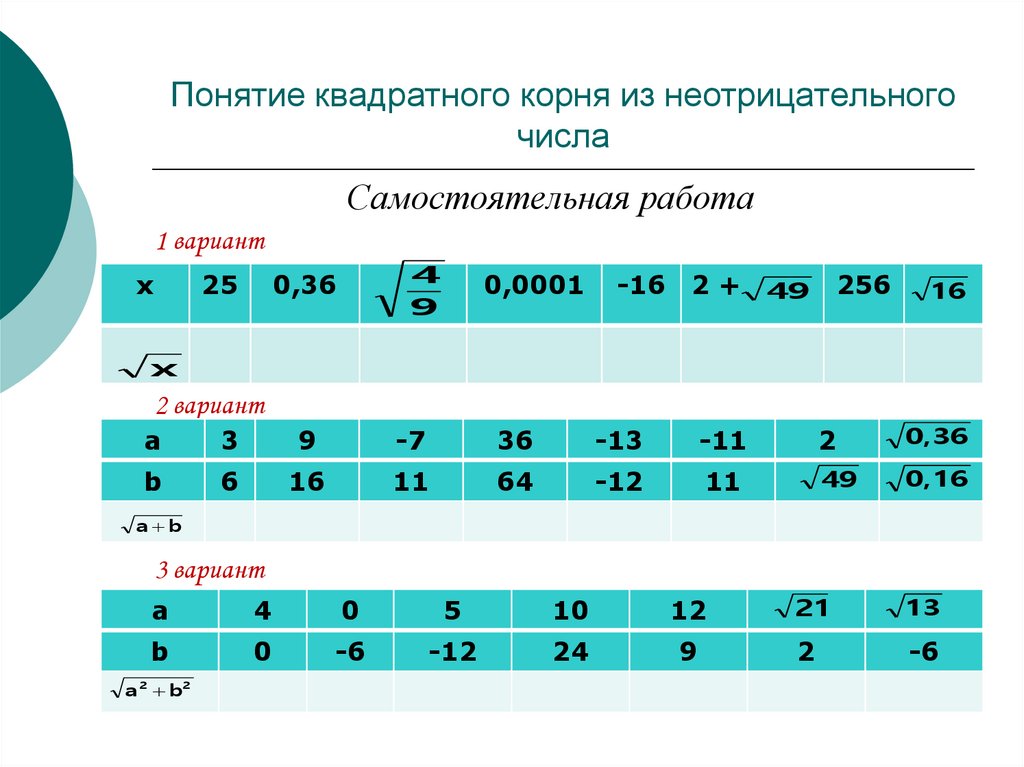
Самостоятельная работа
1 вариант
х
25
4
9
0,36
0,0001
-16 2 + 49
256
16
х
2 вариант
а
3
9
-7
36
-13
-11
2
0,36
b
6
16
11
64
-12
11
49
0,16
а b
3 вариант
а
4
0
5
10
12
21
13
b
0
-6
-12
24
9
2
-6
а 2 b2

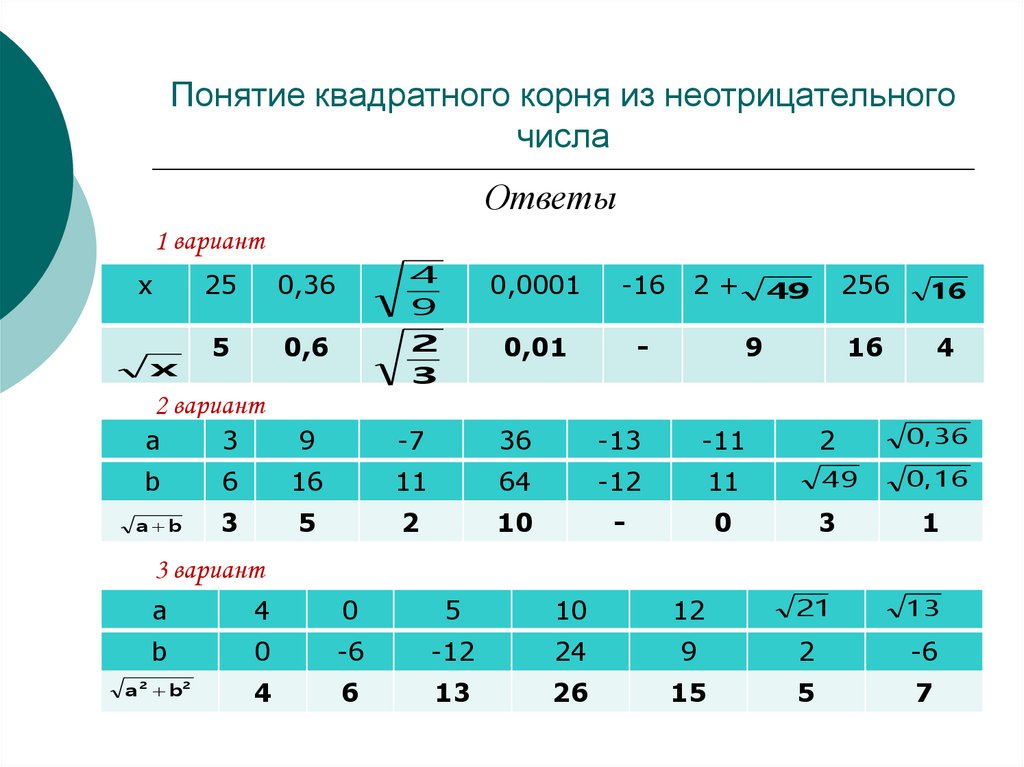
15. Понятие квадратного корня из неотрицательного числа

Ответы
1 вариант
х
х
25
0,36
4
9
0,0001
-16
5
0,6
2
3
0,01
-
2+
49
9
256
16
16
4
2 вариант
а
3
9
-7
36
-13
-11
2
0,36
b
6
16
11
64
-12
11
49
0,16
3
5
2
10
-
0
а b
3
1
21
13
3 вариант
а
4
0
5
10
12
b
0
-6
-12
24
9
2
-6
а 2 b2
4
6
13
26
15
5
7

16.

Понятие квадратного корня из неотрицательного
числа
Итог урока
Сформулируйте определение арифметического
квадратного корня.
При каких значениях а выражение
смысл?
а
имеет
Имеет ли уравнение х 2 а корни при а>0,
a<0, a = 0, и если имеет, то сколько?

17. Понятие квадратного корня из неотрицательного числа

Домашнее задание
Учебник (теория) §12 читать, учить определения.
Учебник (задачник) №№ 312
313
314