Система координат

1.

Автор:
Лебедева Ж.В.

2.

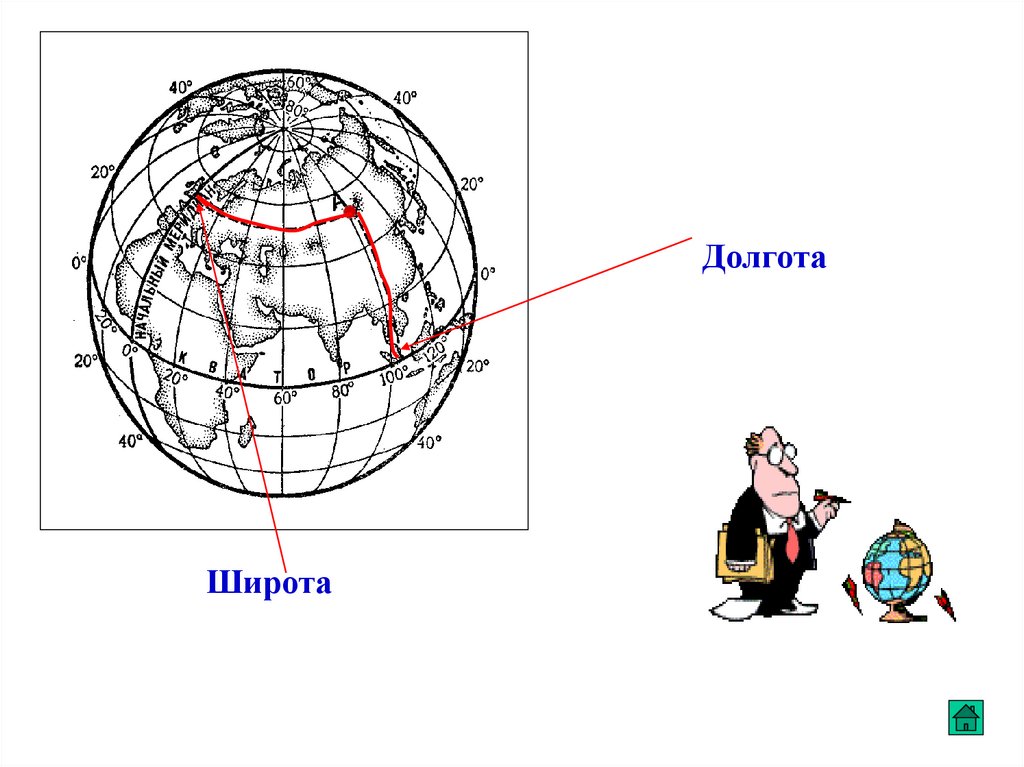
Известно, что:
для определения положения точки на
земной поверхности надо знать ее
географические координаты
• место в зрительном зале
тоже определяется по двум
координатам
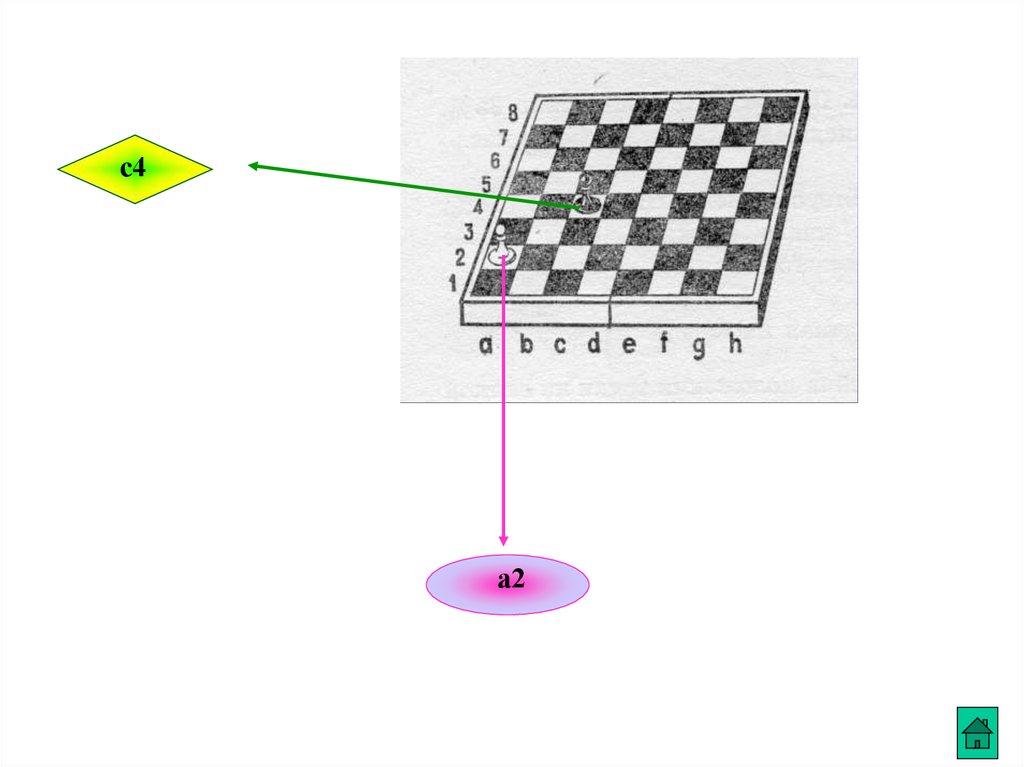
• положение фигуры на
шахматной доске тоже
определяется с помощью
двух координат

3.

Долгота
Широта

4.

1 ряд, 5 место
5 ряд, 8 место
3 ряд, 8 место

5.

с4
а2

6.

у
1
О 1
Начало координат
Оси координат
х

7.

Прямоугольная система координат – гениальное
творение французского математика, философа,
физика и физиолога Рене Декарта (1596 - 1650).
В своей «Геометрии» (1637) Декарт разработал
метод координат, сделавший возможным
изучение свойств геометрических фигур с
помощью алгебры.
Ученый отводил математике особое место, т.к.
считал ее принципы установления истины
образцом для других наук.
В 1649 году Декарт поле долгих колебаний
переезжает в Швецию. Это решение оказалось
для его здоровья роковым.Через полгода он умер
от пневмонии.
Учение Декарта преследовались церковниками.
В 1663 году,уже после смерти ученого, его
сочинения были внесены в «Индекс
запрещенных книг».

8.

Научимся:
1. Находить на координатной плоскости
координаты данной точки
2. Определять положение точки по ее
координатам

9.

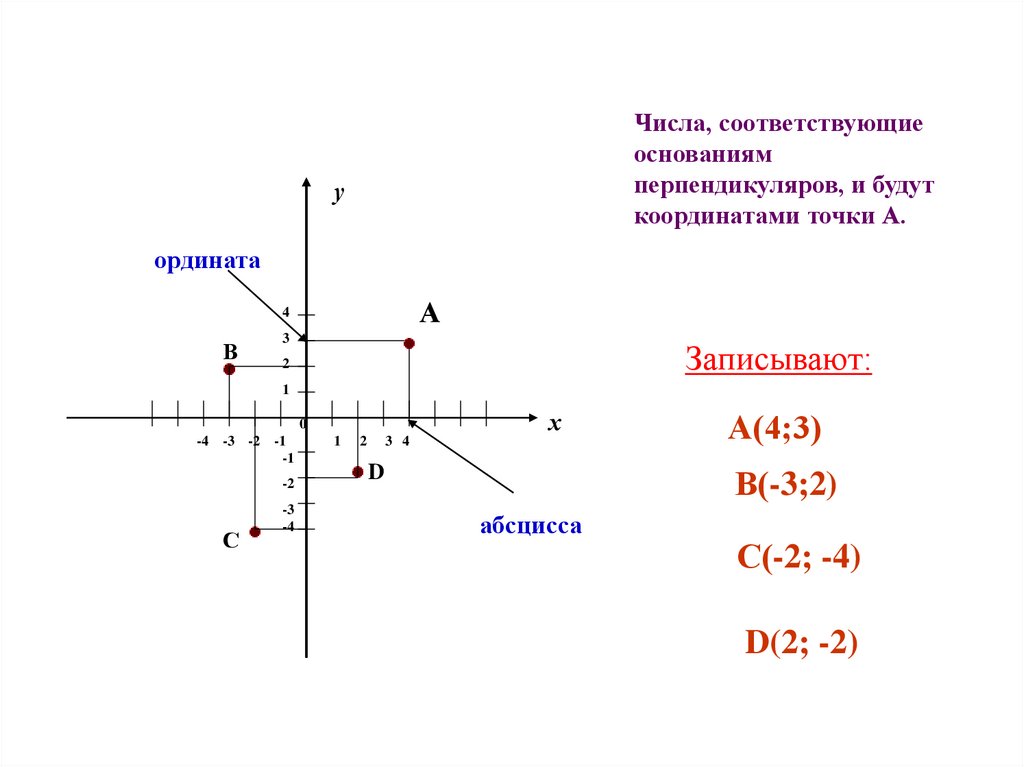
Числа, соответствующие
основаниям
перпендикуляров, и будут
координатами точки А.
у
ордината
А
4
В
3
Записывают:
2
1
0
-4 -3 -2 -1
-1
-2
С
-3
-4
1
2
3 4
х
D
А(4;3)
В(-3;2)
абсцисса
С(-2; -4)
D(2; -2)

10.

Ось ОХ – ось абсцисс
Ось ОУ – ось ординат
у
Точки В и К лежат на оси
абсцисс, их ординаты равны 0:
В(5;0), К(-3;0)
F
4
3
К
2
В
1
0
-4 -3 -2 -1
-1
1
-2
-3
-4
2
3 4
5
х
Точки F и А лежат на оси
ординат, их абсциссы равны 0:
F(0;4), А(0; -4).
А
Начало координат – точка О имеет
координаты, равные нулю: О(0;0).

11.

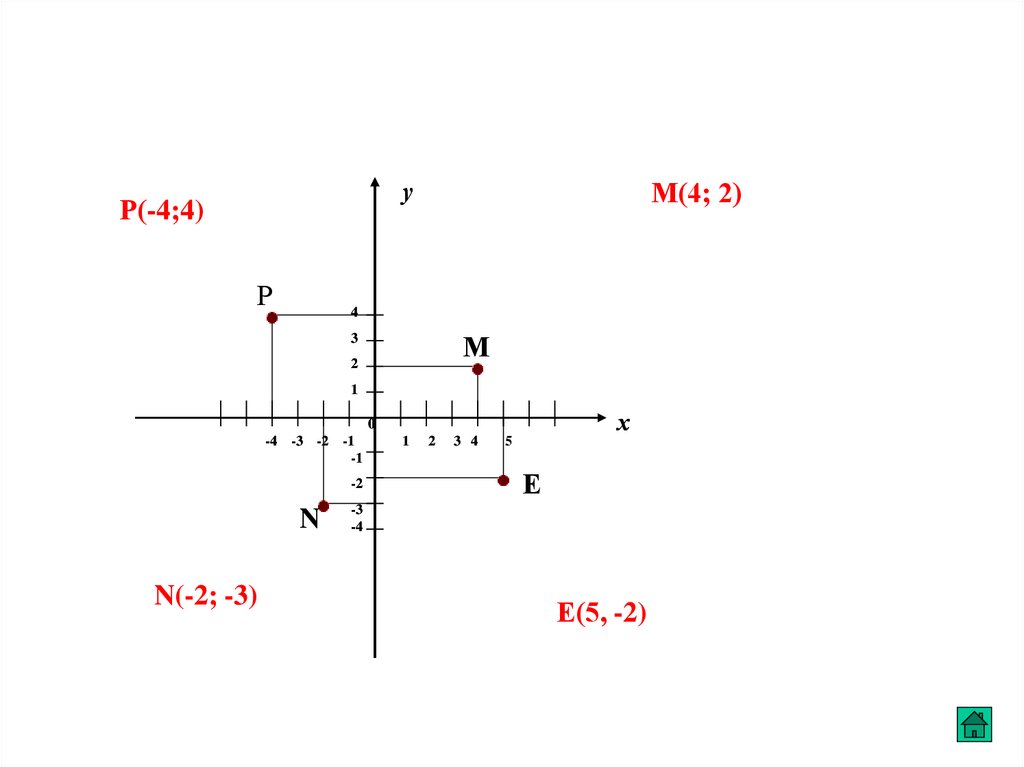
у
Р(-4;4)
Р
М(4; 2)
4
М
3
2
1
х
0
-4 -3 -2 -1
-1
-2
N
N(-2; -3)
1
2
3 4
5
Е
-3
-4
Е(5, -2)

12.

у
12
11
10
9
8
7
6
5
4
3
2
1
0
-8 -7 -6 -5 -4 -3 -2 -1
-1
-2
-3
-4
-5
-6
СТРАУС
-7
-8
1
2
3 4
5 6
7 8
9
10
(0; 0)
(-1; 1)
(-3;1)
(-2; 3)
(-3; 3)
(-4; 6)
(0; 8)
(2;5)
(2;11)
(6; 10)
(3; 9)
(4; 5)
(3; 0)
(2; 0)
(1; -8)
(3;
-7)
(0; -8)
х (0; 0)