Похожие презентации:
Начертательная геометрия. Лекция 3
1. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Лекция 3. Плоскость
Пьянкова Жанна Анатольевна,доцент каф. «ПиЭА», канд. пед. наук
1
2. Ортогональные проекции плоскости
• Плоскость и способы задания ее начертеже
• Положение плоскости относительно
плоскостей проекций
• Прямая и точка в плоскости
• Главные линии плоскости
• Прямая и точка в плоскости
• Относительное положение двух
плоскостей
2
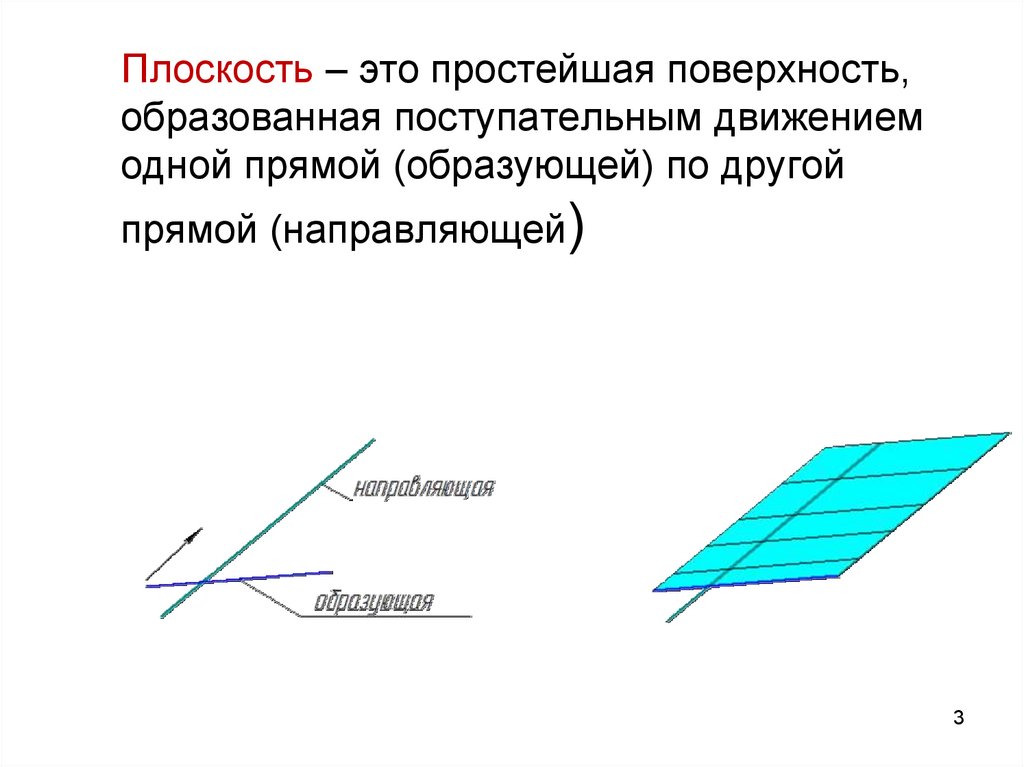
3. Плоскость – это простейшая поверхность, образованная поступательным движением одной прямой (образующей) по другой прямой
(направляющей)3
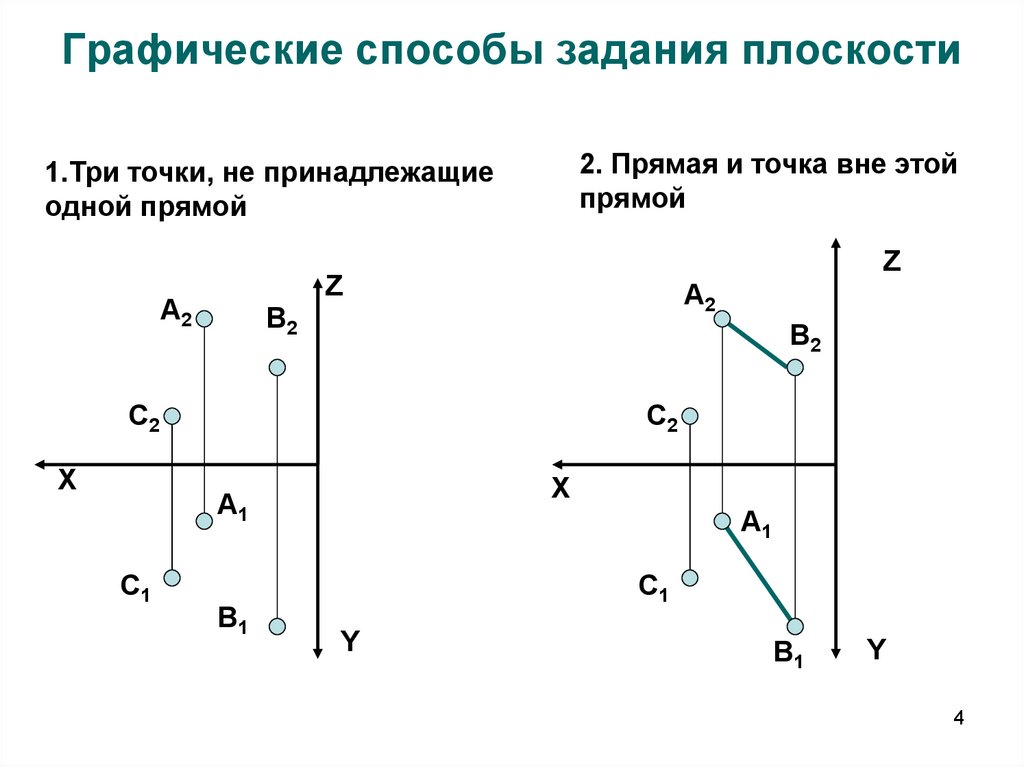
4. Графические способы задания плоскости
2. Прямая и точка вне этойпрямой
1.Три точки, не принадлежащие
одной прямой
Z
Z
А2
А2
В2
В2
C2
X
C2
X
А1
C1
В1
А1
C1
Y
В1
Y
4
5.
3. Параллельные прямые4. Пересекающиеся прямые
Z
a2
а2
b2
b2
X
Z
К2
X
b1
а1
a1
К1
Y
b1
Y
5
6.
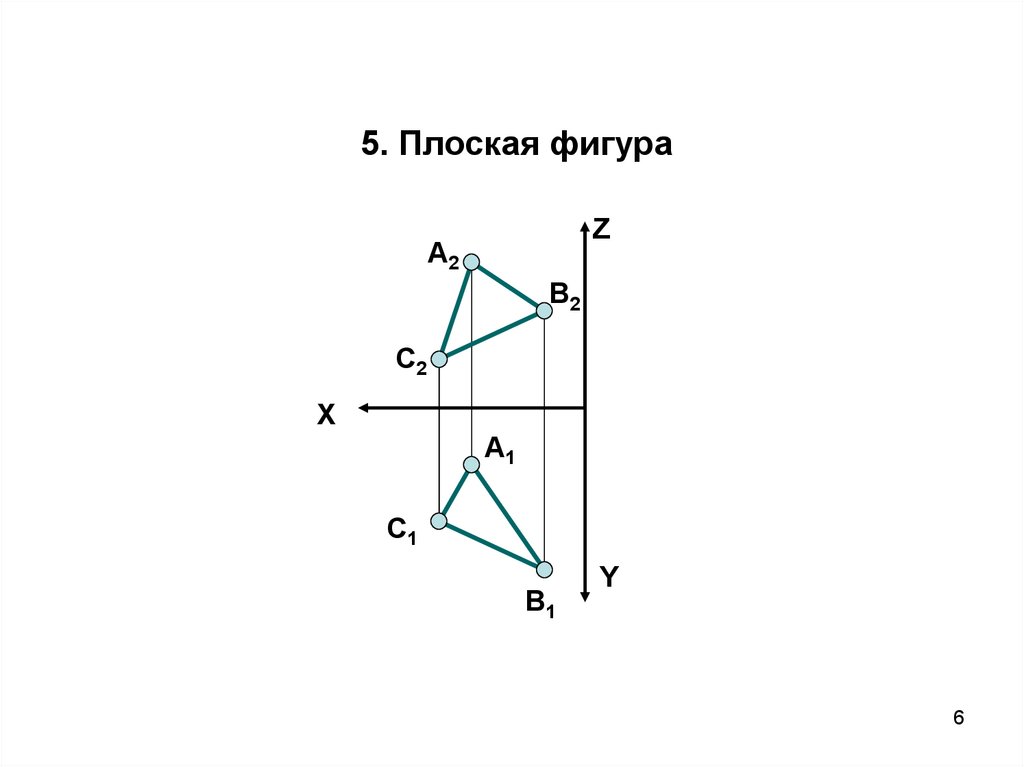
5. Плоская фигураZ
А2
В2
C2
X
А1
C1
В1
Y
6
7.
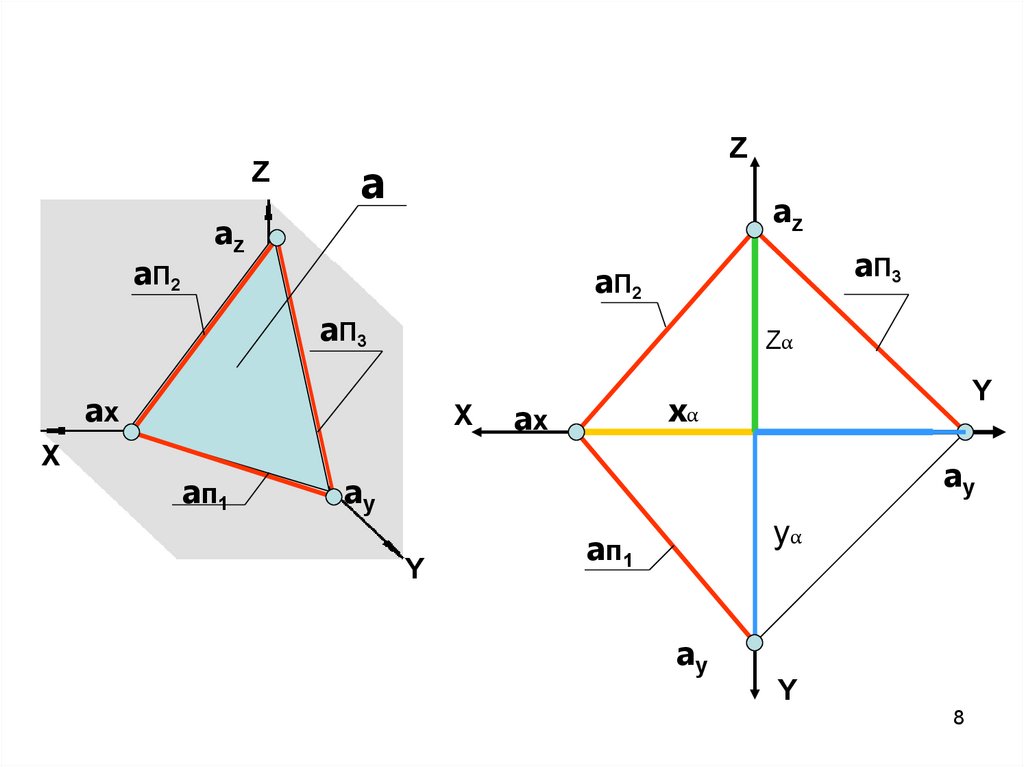
6. Следы плоскости – линии пересечения даннойплоскости с плоскостями проекций
Z
a П2
az
a-плоскость;
a
aп1 - горизонтальный след
плоскости a;
aп2 - фронтальный след
плоскости a;
a П3
ax
X
a п1
aп3 - профильный след
плоскости a;
ay
ax, ay, az - точки схода следов.
Y
7
8.
Za П2
Z
a
az
az
a П3
a П2
a П3
Zα
ax
X
X
a п1
Y
xα
ax
ay
ay
Y
yα
a п1
ay
Y
8
9. Особенности способа задания плоскости следами
• Этот способ является частным случаем заданияплоскости двумя пересекающимися прямыми
• Каждый след совпадает со своей одноименной
проекцией, другая проекция следа принадлежит оси
проекций (вторую проекцию следа принято не обозначать)
• Угол между следами плоскости на эпюре не равен углу
между ее следами в пространстве
• По расположению следов плоскости на эпюре легко
представить расположение самой плоскости в
пространстве
9
10. Положение плоскости относительно плоскостей проекций:
• Параллельно – плоскости уровня;• Перпендикулярно – проецирующие
плоскости
• Под любым углом, отличным от
прямого – плоскости общего положения
10
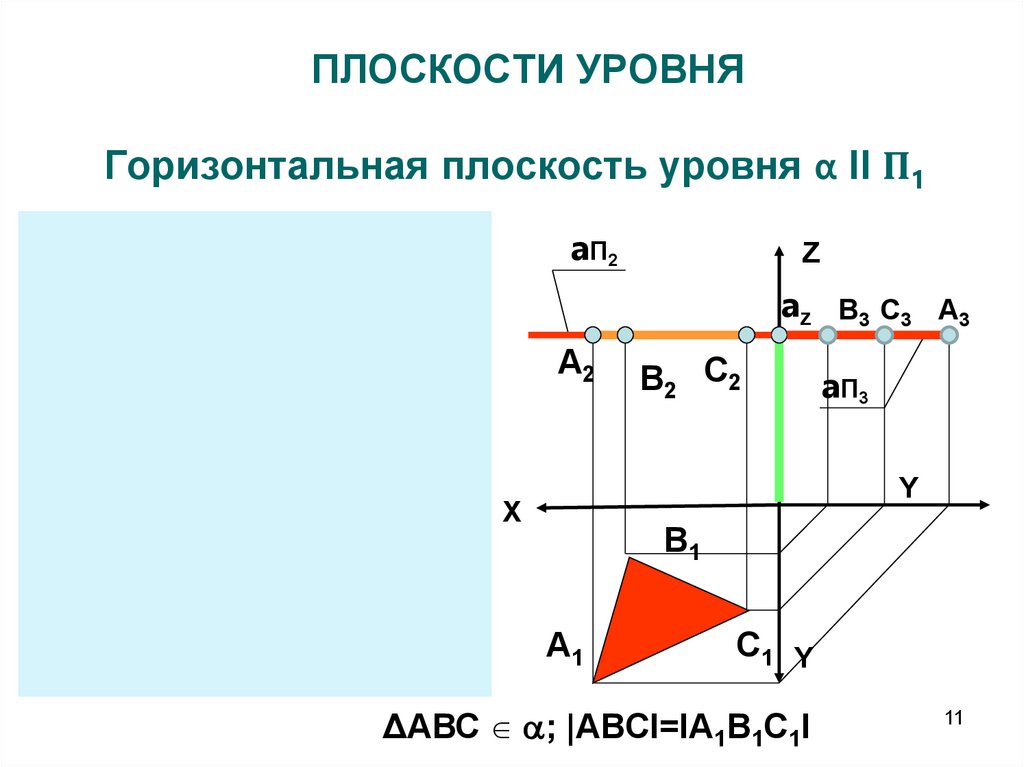
11. ПЛОСКОСТИ УРОВНЯ
Горизонтальная плоскость уровня α II П1α П2
α
Z
В2 С α z
2
А2
aП2
az В3 С3 А3
α П3
А2
С1
Y
a П3
В1
В1
А1
В2 С2
Y
X
X
Z
А1
С1 Y
ΔАВС ; |ABCI=IA1B1C1I
11
12.
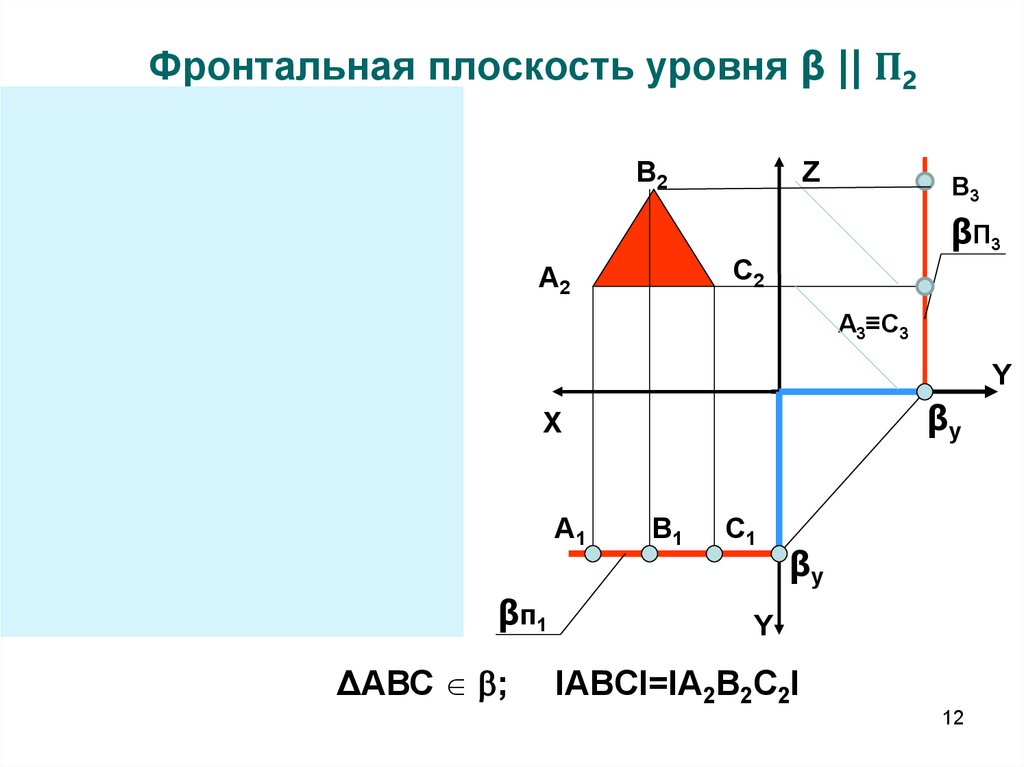
Фронтальная плоскость уровня β || П2Z
β
В2
Z
В3
βП3
С2
А2
βП3
А3≡С3
Y
X
βп1
βy
X
βy
А1
Y
βп1
ΔАВС ;
В1
С1
βy
Y
IABCI=IA2B2C2I
12
13.
Профильная плоскость уровня || П3Z
γ
γ П2
γ П2
X γx
X
Z
γx
Y
γ п1
Y
γ п1
Y
13
14. Особенности чертежа плоскостей уровня
• Фигуры, принадлежащие плоскостям уровня,проецируются в натуральную величину на
параллельную плоскость проекций
• На другие плоскости проекций фигуры,
принадлежащие плоскостям уровня,
проецируются в прямую линию
14
15.
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИГоризонтально проецирующая плоскость
┴П1
ΔАВС
Z
a П2
a П2
a
В2
Z
a П3
А2
X
С2
a П3
ax
ax
ay
X
a п1
ay
А1
Y
y
В1
Y
a п1
С1
ay
15
Y
16.
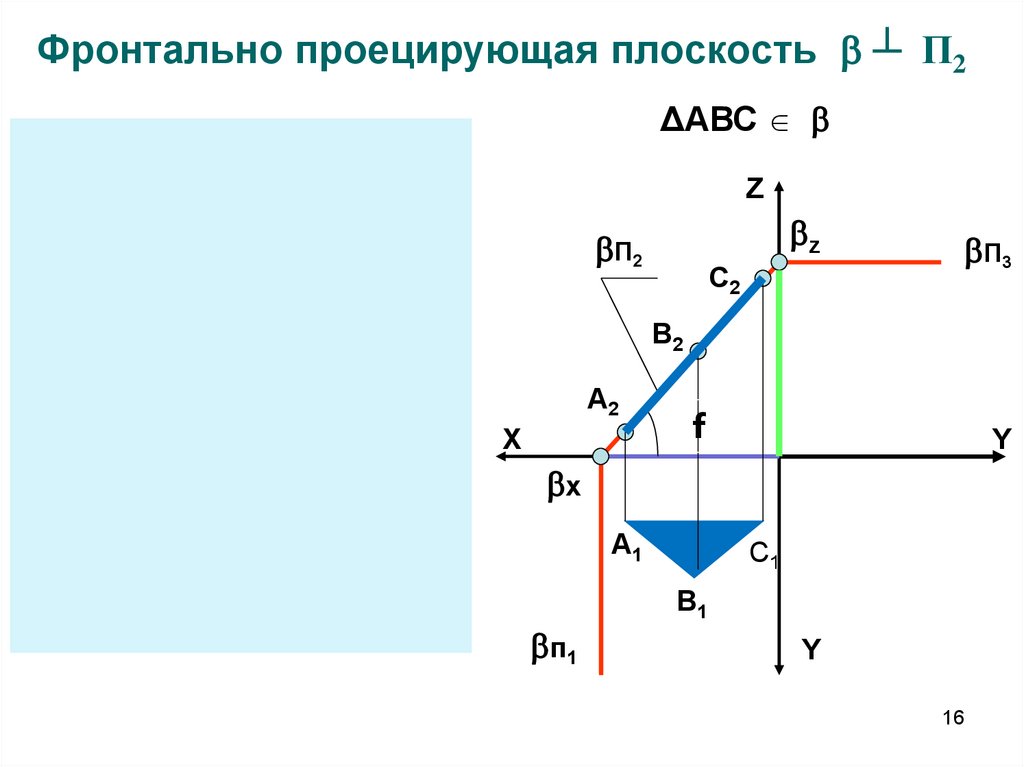
Фронтально проецирующая плоскость ┴ П2ΔАВС
Z
П2
Z
z
П2
z
С2
П3
В2
П3
x
А2
X
f
Y
x
X
П1
А1
С1
В1
Y
п1
Y
16
17.
Профильно проецирующая плоскость ┴ П3ΔАВС
Z
П2
Z
П2
z
В3
φ
X
X
П3
А 3=С 3
ψ
П3
п1
z
Y
y
y
п1
Y
y
Y
17
18.
Особенности чертежа проецирующихплоскостей
• Фигуры, принадлежащие проецирующим
плоскостям, на перпендикулярную плоскость
проекций проецируются в прямую линию
(вырожденная проекция)
• Угол наклона между вырожденной проекцией
и осями координат равен углу между
заданной плоскостью и плоскостью проекций
18
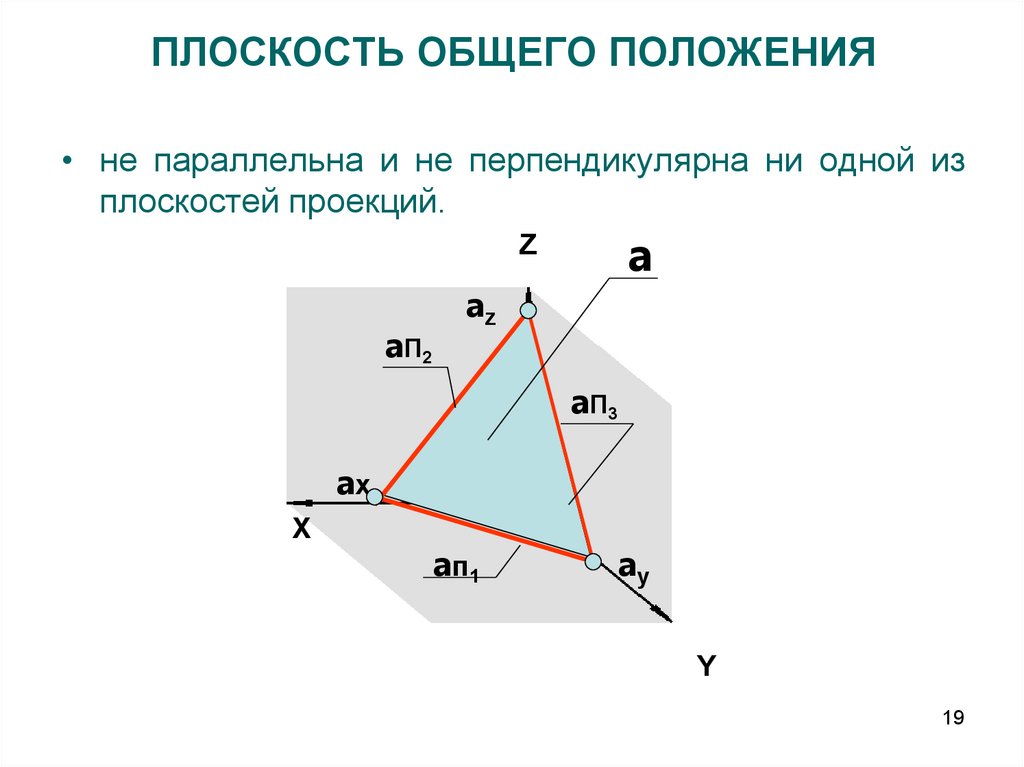
19. ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
• не параллельна и не перпендикулярна ни одной изплоскостей проекций.
a
Z
a П2
az
a П3
ax
X
aп1
ay
Y
19
20.
ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙПЛОСКОСТИ
1. Точка принадлежит плоскости, если она принадлежит
прямой в этой плоскости
2. Прямая принадлежит плоскости, если она имеет с этой
плоскостью две общие точки
3. Если прямая принадлежит плоскости, то её следы
лежат на одноименных следах плоскости
20
21.
Принадлежит ли точка А плоскости α?Z
aп2
точка А плоскости α
А2
X
не принадлежит
ax
А1
a П1
Y
21
22. Главные линии плоскости
• Горизонталь плоскости• Фронталь плоскости
• Линия ската плоскости
22
23.
Горизонталь плоскостиZ
az
a
Горизонталь h параллельна
горизонтальной
плоскости
проекций
и
принадлежит плоскости α
a П2
a П3
ax
X
a п1
ay
Y
23
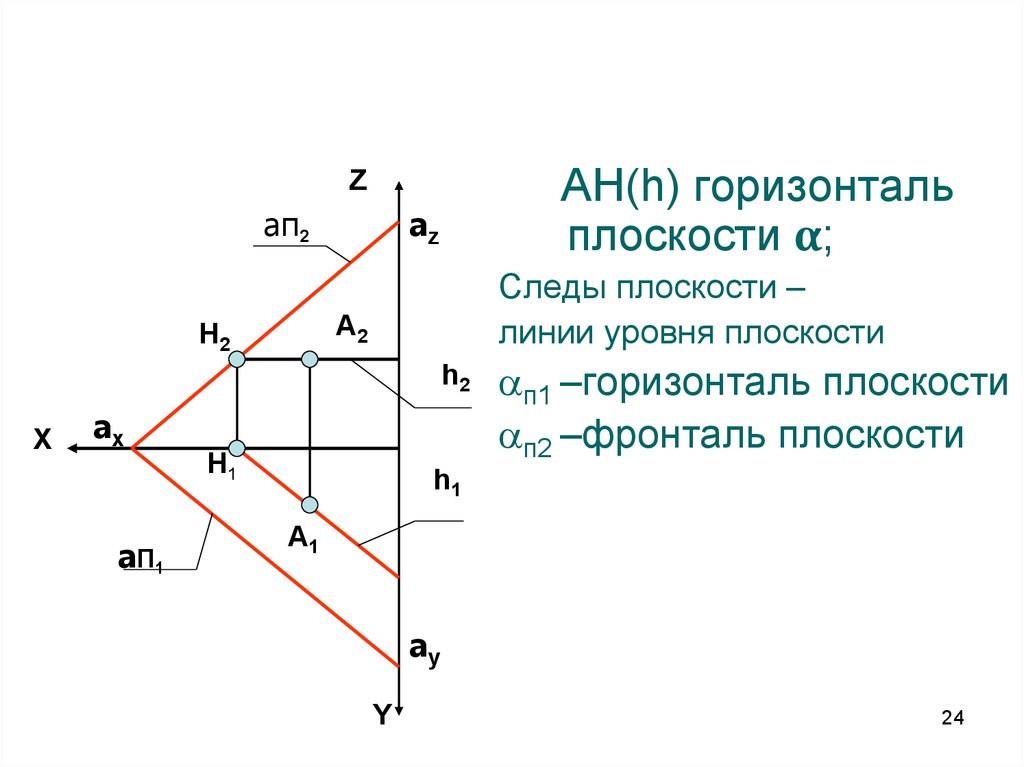
24.
AН(h) горизонтальплоскости α;
Z
aп2
az
Следы плоскости –
линии уровня плоскости
А2
Н2
h2
X
ax
a П1
Н1
п1 –горизонталь плоскости
п2 –фронталь плоскости
h1
А1
ay
Y
24
25.
Горизонталь плоскости треугольникаВ2
AH(h)–
горизонталь
ΔАВС
H2
А2
X
С2
А1
С1
H1
В1
25
26.
Фронталь плоскостиZ
aп2
az
АF (f)- фронталь
плоскости α
А2
f2
ax
F2
X
F1
А1
f1
a П1
ay
Y
26
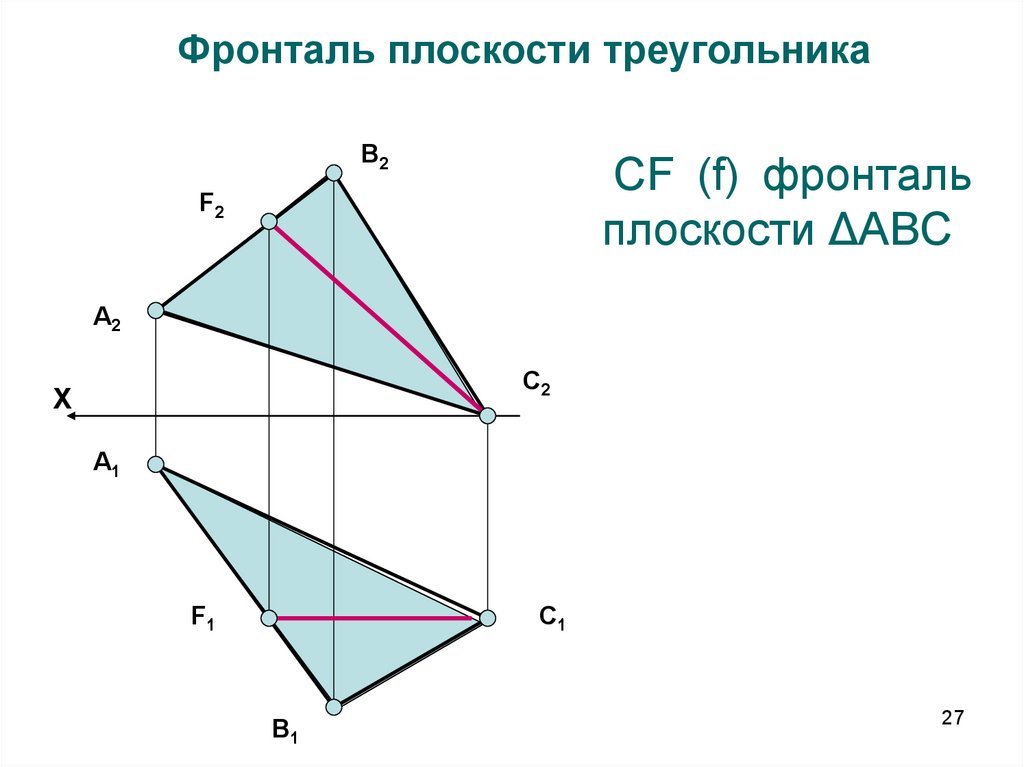
27.
Фронталь плоскости треугольникаВ2
СF (f) фронталь
плоскости ΔАВС
F2
А2
С2
X
А1
С1
F1
В1
27
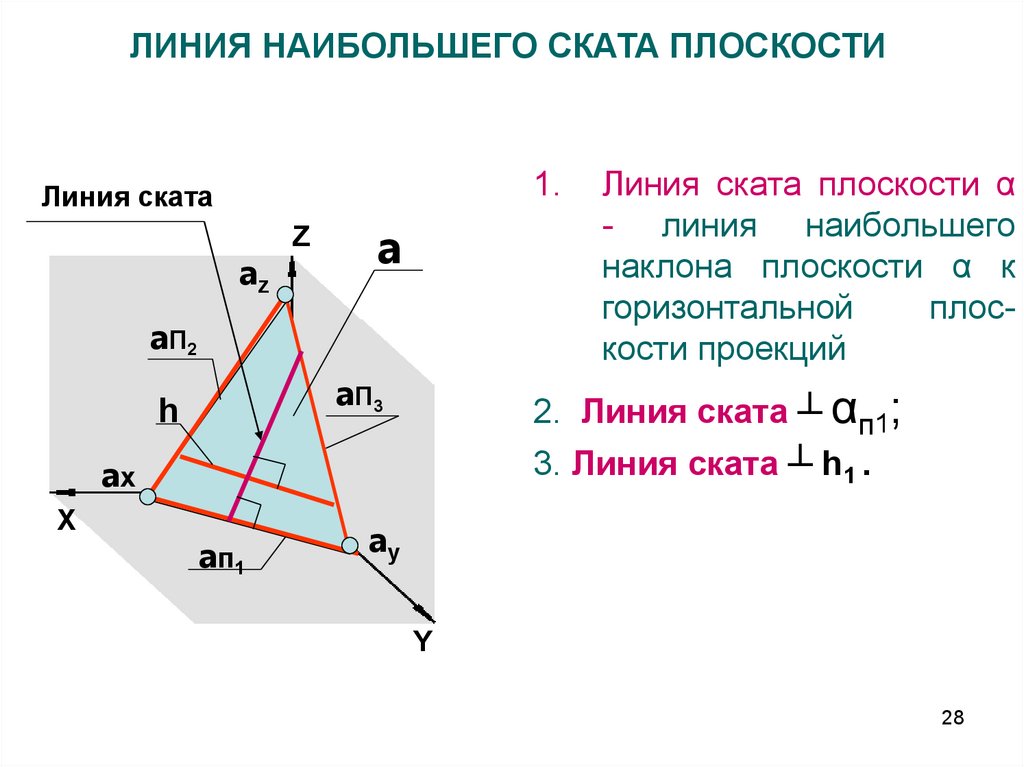
28.
ЛИНИЯ НАИБОЛЬШЕГО СКАТА ПЛОСКОСТИ1.
Линия ската
az
Z
a
a П2
aП3
h
2. Линия ската ┴ αп1;
3. Линия ската ┴ h1 .
ax
X
Линия ската плоскости α
- линия наибольшего
наклона плоскости α к
горизонтальной
плоскости проекций
a п1
ay
Y
28
29.
Линия ската треугольникаВ2
1. В1D1 ┴ А1H1
2. ВD – линия
ската
треугольника
H2
А2
D2
С2
X
А1
D1
С1
С1
H1
В1
29
30. ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ
3031. Взаимное положение прямой и плоскости
Прямая принадлежит плоскостиПрямая параллельна плоскости
Прямая пересекает плоскость
Прямая перпендикулярна плоскости
31
32. Прямая параллельна плоскости,
если она параллельна хотя бы однойпрямой, лежащей в этой плоскости
32
33. Пересечение прямой с плоскостью
Аксиома:Если прямая не принадлежит плоскости
и не параллельна ей, то она эту
плоскость пересекает
33
34.
п2п2
а2
а2
К2
К2
X
X
O
O
К1
a1
К1
п1
a1
• Точка пересечения прямой и плоскости
частного положения определяется на
пересечении следа плоскости и проекции
прямой
п1
34
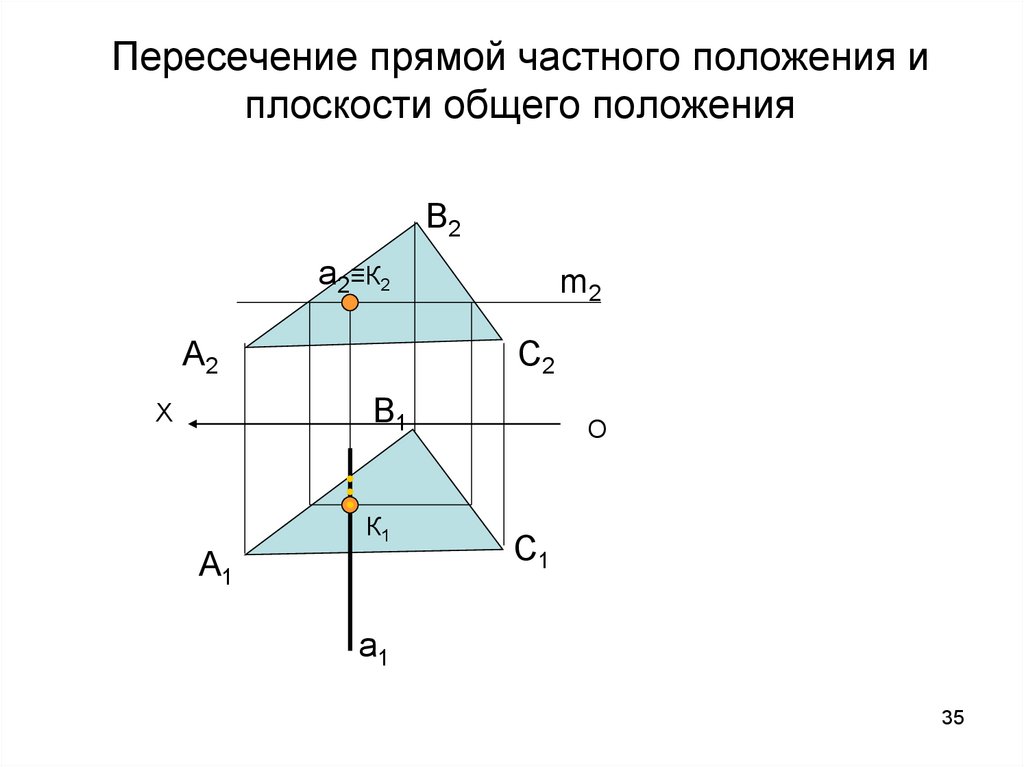
35. Пересечение прямой частного положения и плоскости общего положения
В2a2≡К2
А2
m2
С2
В1
X
А1
К1
О
С1
a1
35
36.
СПОСОБ ВСПОМОГАТЕЛЬНЫХ СЕКУЩИХПЛОСКОСТЕЙ
1. Через
прямую проводят плоскость частного
положения α ┴ П1.
2. Определяют линию пересечения заданной
плоскости и введенной плоскости α.
3. Определяют точку пересечения заданной
прямой и построенной линии пересечения.
Это искомая точка пересечения заданной
плоскости и прямой а.
4. Определяют видимость заданной прямой.
36
37.
B2αп2
a2
К2
12
С2
22
A2
B1
αп1
11
К1
A1
C1
21
a1
Видимость прямой определяют по конкурирующим
точкам
37
38.
На горизонтальной плоскости проекций видима точка С, имеющаябОльшую координату Z,
на фронтальной плоскости проекций видима точка А, имеющая
бОльшую координату Y.
С2
А2 Ξ (В2)
D2
X
В1
(D1) Ξ C1
А1
38
39.
Определение видимости прямойB2
12 Ξ(32)
К2
42
22
A2
31
С2
B1
11 К1
C1
(21) Ξ41
A1
39
40. Перпендикулярность прямой и плоскости
Теорема:Прямая перпендикулярна к плоскости,
если она перпендикулярна двум
пересекающимся прямым этой
плоскости
40
41. Свойство перпендикуляра к плоскости
Если прямая перпендикулярна плоскости, тоее горизонтальная проекция
перпендикулярна горизонтальной проекции
горизонтали плоскости (Г.П.Г.) или ее
горизонтальному следу, а ее фронтальная
проекция перпендикулярна фронтальной
проекции фронтали плоскости (Ф.П.Ф.) или
ее фронтальному следу
41
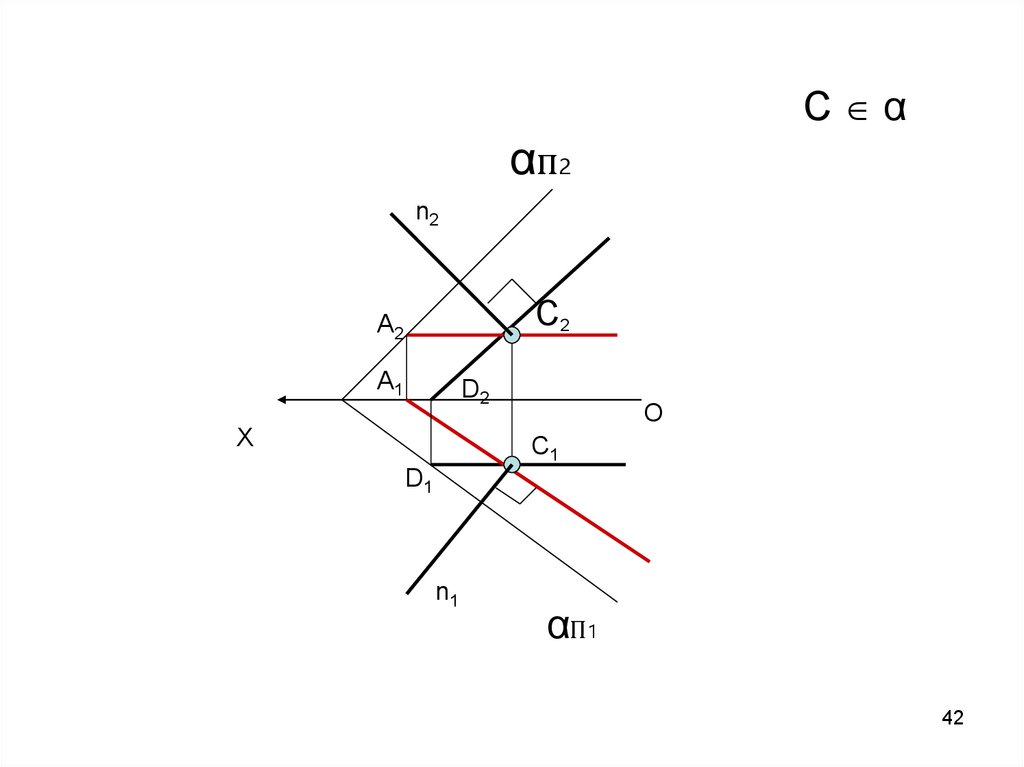
42.
C ααп2
n2
С2
А2
А1
D2
X
O
С1
D1
n1
αП1
42
43. Взаимное положение двух плоскостей
Две плоскости могут быть:Параллельны друг другу;
Пересекаться друг с другом;
Перпендикулярны друг другу
43
44. Условие параллельности двух плоскостей
Теорема:Если две пересекающиеся прямые одной
плоскости параллельны двум
пересекающимся прямым другой
плоскости, то такие плоскости
параллельны друг другу.
Следствие:
Если плоскости параллельны, то их
одноименные следы также параллельны
44
45. Пересечение двух плоскостей
Для построения линии пересечениядвух плоскостей достаточно иметь две
точки, общие к обеим плоскостям или
одну общую точку и направление линии
пересечения
Если плоскости заданы следами, то
общие точки находятся в пересечении
одноименных следов
45
46.
B2αп2
F2
К2
C2
X
αп1
A2
B1
O
F1
К1
C1
A1
• Линия пересечения фронтально-проецирующей
плоскости и плоскости общего положения определяется по точкам пересечения сторон треугольника
ΔАВС и фронтального следа плоскости α
46
47. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
Для построения линии пересеченияплоскостей достаточно поочередно
найти две точки пересечения двух
ребер одной фигуры с другой фигурой.
Соединив эти точки, мы получим линию
пересечения двух плоскостей.
47
48. Задача
Построить линию пересечениятреугольников ΔABC и ΔDEF.
A(100, 20, 20), B(65, 70, 70), C(10, 30,25),
D(90, 10, 55), E(45, 70, 0), F(20, 10, 65)
48
49.
4950.
1. АВС ∩ DE = КDE ┴ П2
2. АВС ∩ EF = L
EF ┴ П2
50
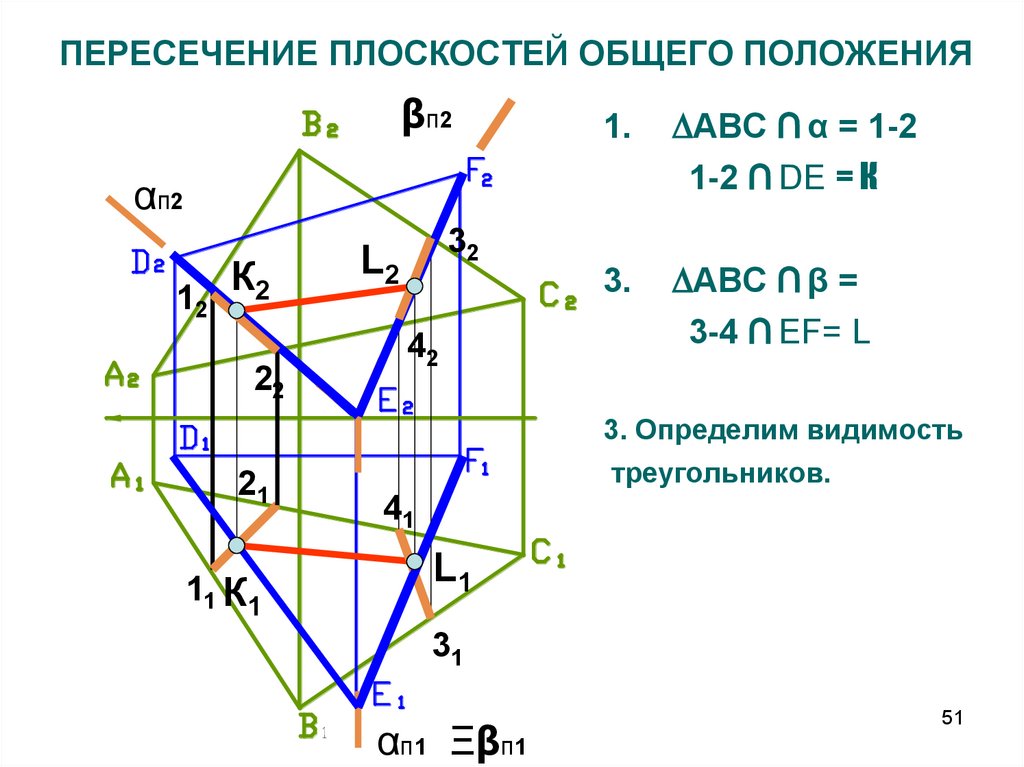
51. ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ ОБЩЕГО ПОЛОЖЕНИЯ
βп21.
АВС ∩ α = 1-2
1-2 ∩ DE = К
3.
АВС ∩ β =
3-4 ∩ EF= L
αп2
К
12 2
22
21
11 К1
32
L2
42
3. Определим видимость
треугольников.
41
L1
31
αп1 Ξβп1
51
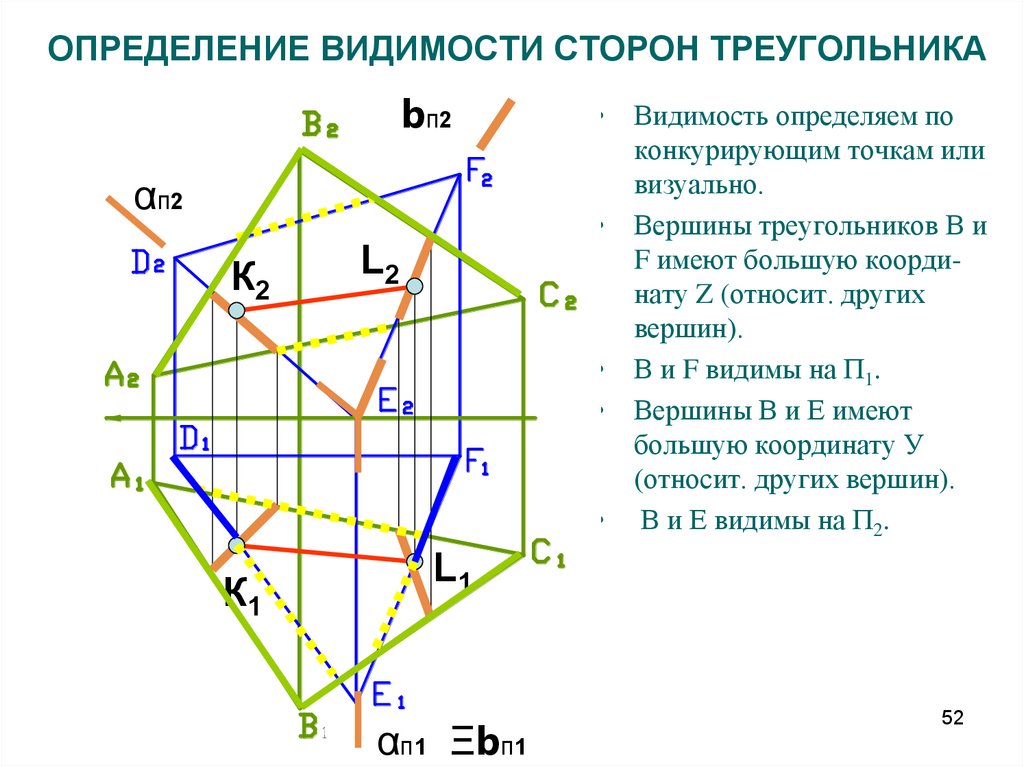
52. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ СТОРОН ТРЕУГОЛЬНИКА
bп2αп2
К2
К1
L2
• Видимость определяем по
конкурирующим точкам или
визуально.
• Вершины треугольников В и
F имеют большую координату Z (относит. других
вершин).
• В и F видимы на П1.
• Вершины В и Е имеют
большую координату У
(относит. других вершин).
• В и Е видимы на П2.
L1
αп1 Ξbп1
52
53.
5354.
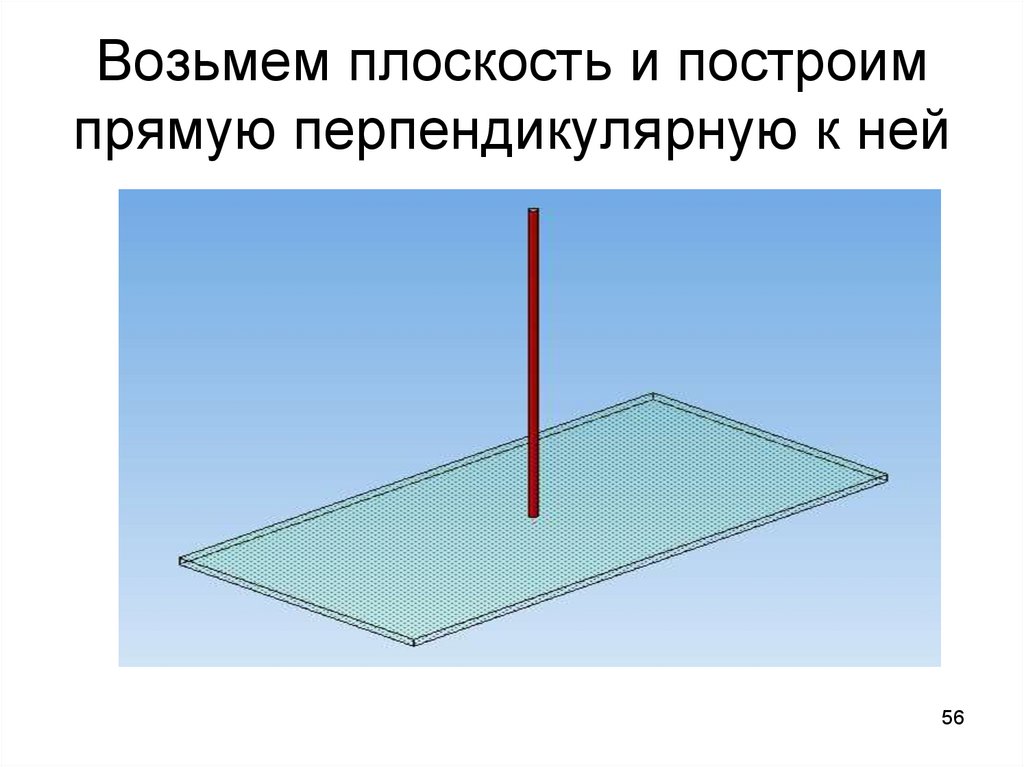
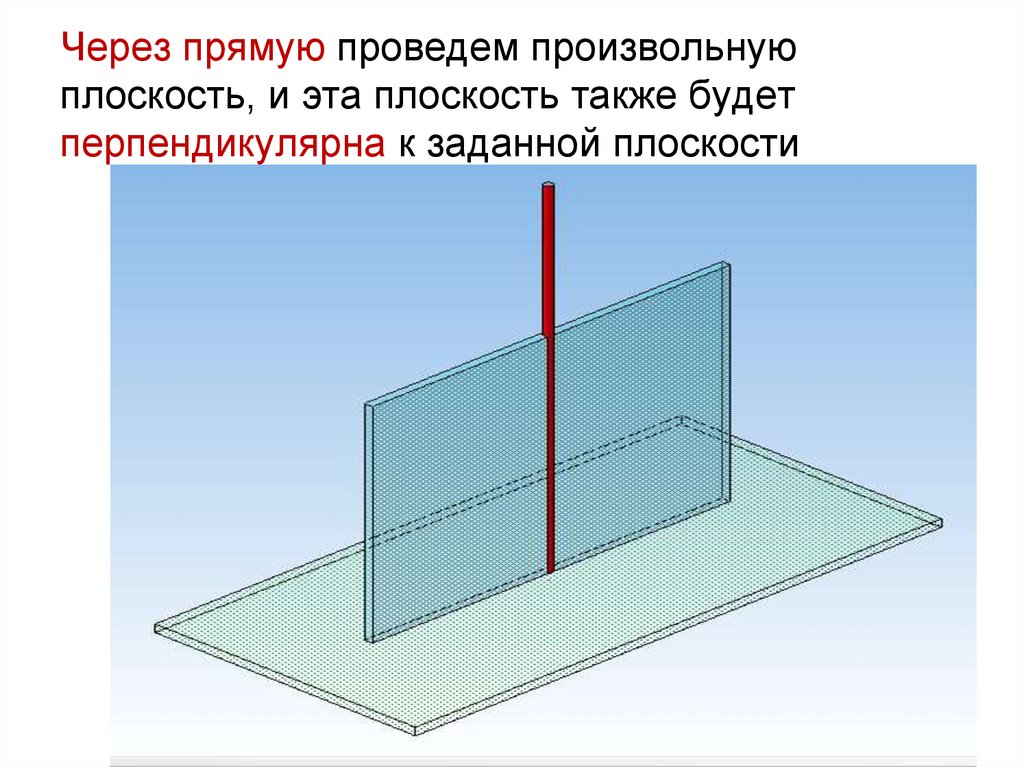
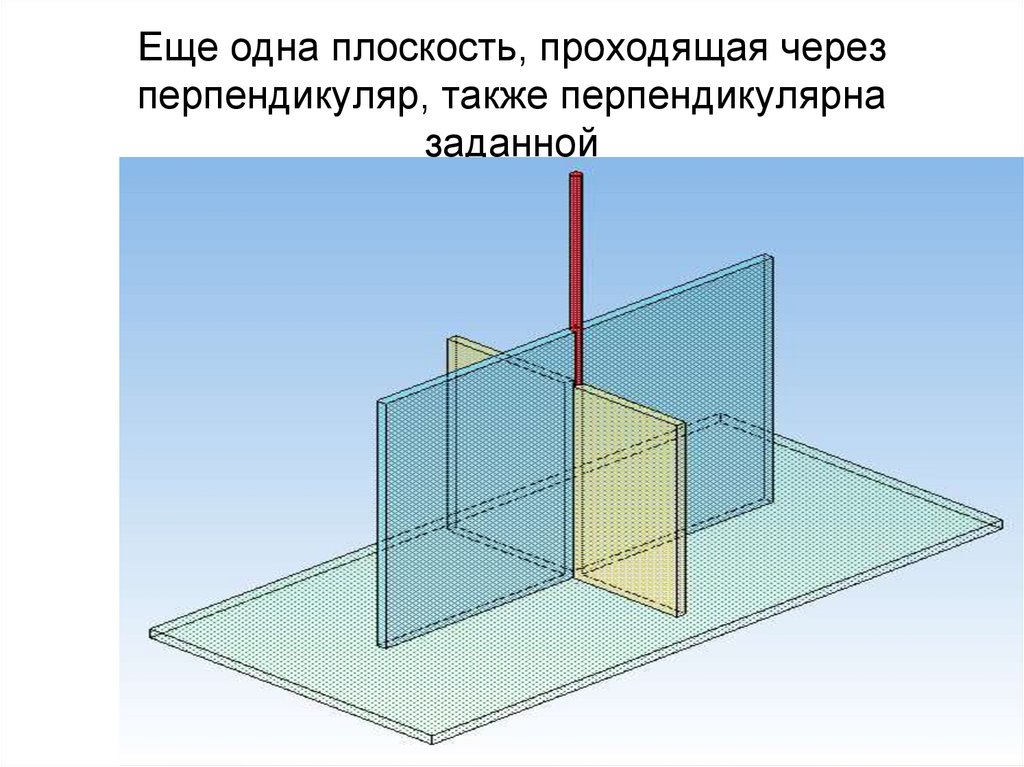
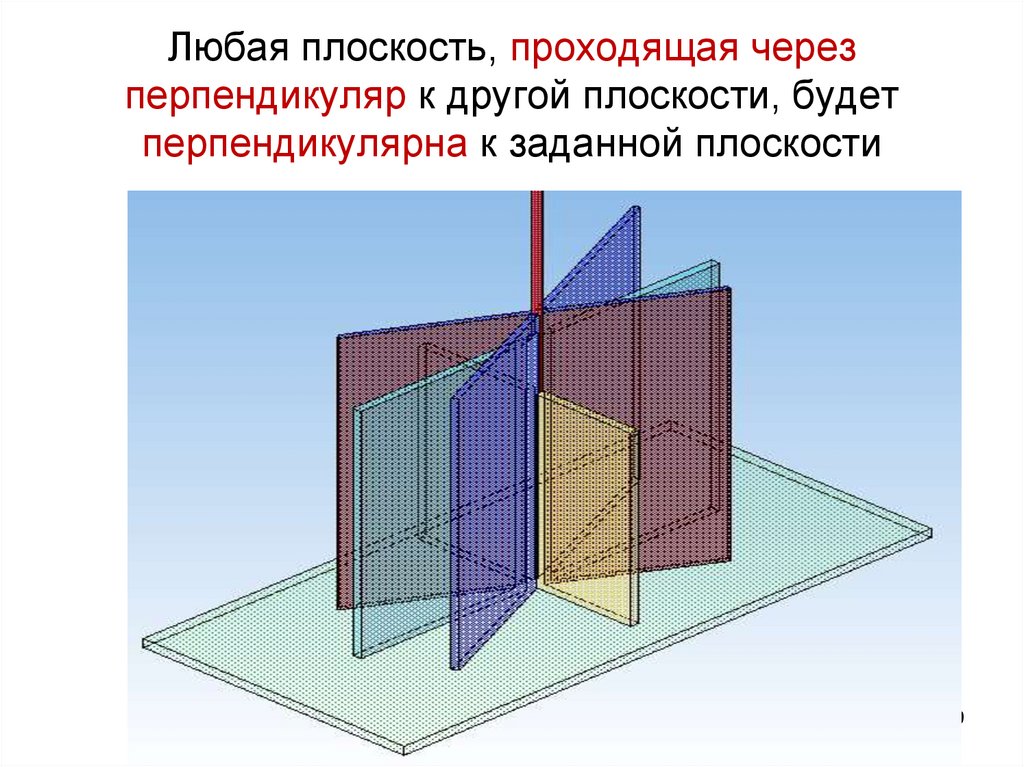
5455. Взаимная перпендикулярность двух плоскостей
Аксиома:Две плоскости взаимно
перпендикулярны, если одна из них
проходит через перпендикуляр к другой
плоскости
55








































 Инженерная графика
Инженерная графика








