Похожие презентации:
Функция y=sinx. Свойства. Преобразование графиков
1.
Функция y=sinxСвойства.
Преобразование
графиков.
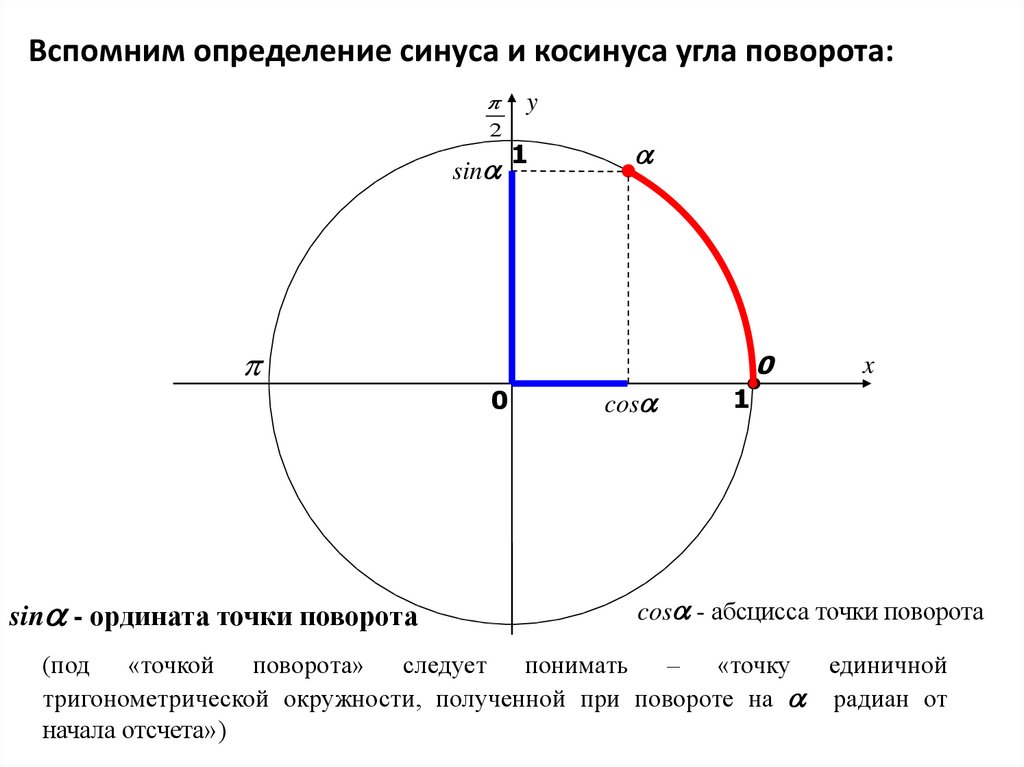
2. Вспомним определение синуса и косинуса угла поворота:
2sin
1
0
0
sin - ордината точки поворота
y
cos
x
1
cos - абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной
тригонометрической окружности, полученной при повороте на радиан от
начала отсчета»)
3.
На оси абсцисс координатной плоскости Оху будем отмечатьточки, соответствующие различным углам поворота, а на
оси ординат – значения синусов этих углов.
6
5
4
2
y
y
3
1
2
1
1
0
0
1 x
x
0
1 2 3 4 5
2
6
Получили график функции y=sinx на промежутке [0; ].
4. Построение графика функции y = sin x
y2
1
0
0
-1
8
4
3 5 3 7
8 2 8 4 8
x
5.
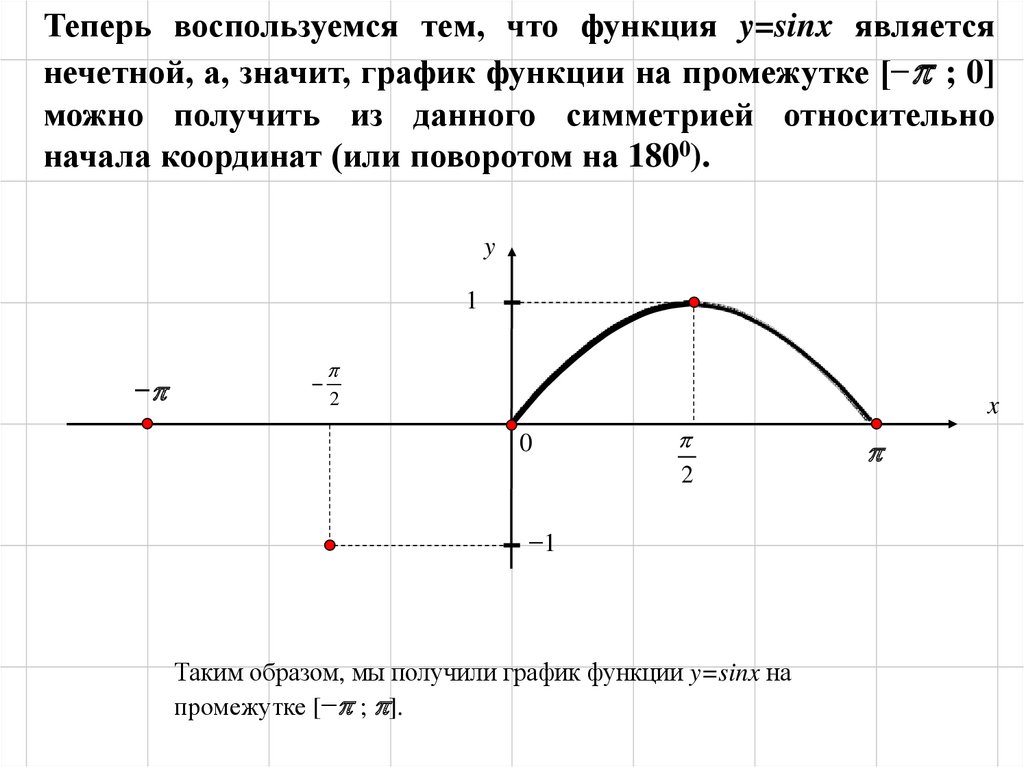
Теперь воспользуемся тем, что функция y=sinx являетсянечетной, а, значит, график функции на промежутке [− ; 0]
можно получить из данного симметрией относительно
начала координат (или поворотом на 1800).
y
1
−
2
x
0
2
−1
Таким образом, мы получили график функции y=sinx на
промежутке [− ; ].
6.
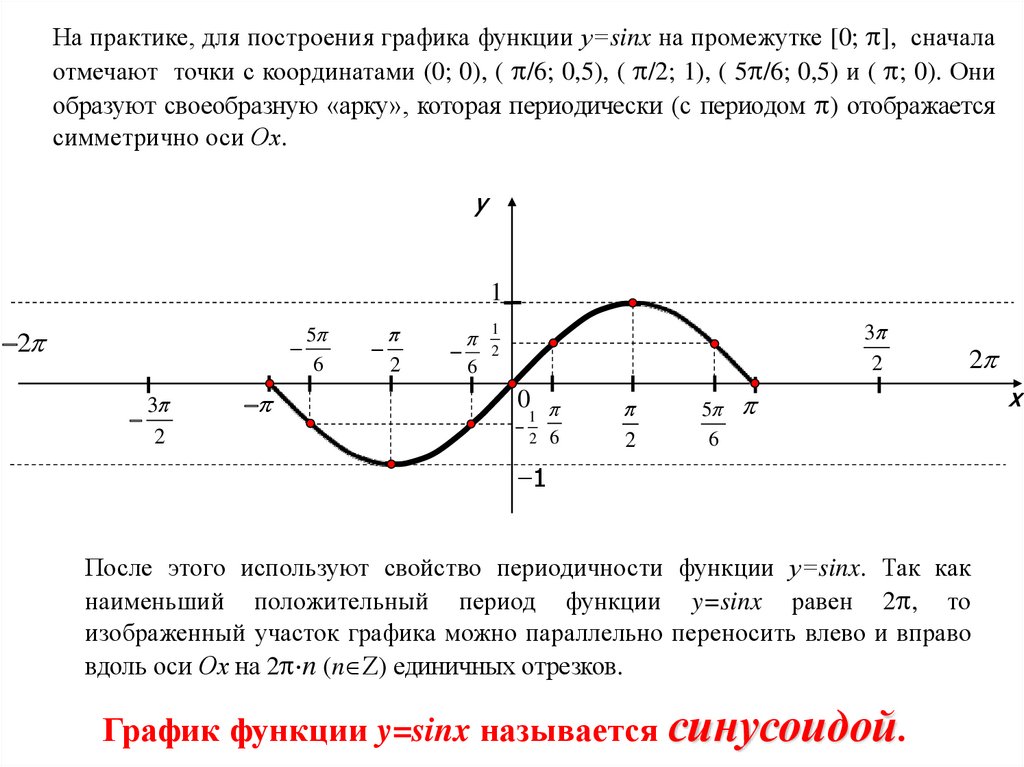
На практике, для построения графика функции у=sinx на промежутке [0; ], сначалаотмечают точки с координатами (0; 0), ( /6; 0,5), ( /2; 1), ( 5 /6; 0,5) и ( ; 0). Они
образуют своеобразную «арку», которая периодически (с периодом ) отображается
симметрично оси Ох.
y
1
5
6
2
3
2
2
3
2
1
2
6
0
1
6
2
2
5
6
2
−1
После этого используют свойство периодичности функции у=sinx. Так как
наименьший положительный период функции y=sinx равен 2 , то
изображенный участок графика можно параллельно переносить влево и вправо
вдоль оси Ох на 2 n (n ) единичных отрезков.
График функции y=sinx называется синусоидой.
x
7.
8. Заход Солнца
ДатаВремя
Дата
Время
1.1
15.59
1.7
20.25
1.2
16.45
1.8
19.53
1.3
17.37
1.9
18.53
1.4
18.39
1.10
17.31
1.5
19.28
1.11
16.30
1.6
20.18
1.12
15.51
9. С помощью отрывного календаря нетрудно отметить момент захода Солнца на 1-е число каждого месяца и, соединив полученные точки
плавной линией, построить график,взяв в качестве оси абсцисс среднее
время захода Солнца – 18ч
10. График захода Солнца
времядата
11. Решение упражнений
12.
yy = sin x
2
2
т
3
2
1
-1
2
x
3
2
2
13.
yED((yy))::yx R1; 1
x
1
2 3
2
2
-1
2
3
2
2
3
=2n ;n;n, n
xy = 0 x 2
2 nZ
22
22
14.
yy 00x 0;
y
x
1
2 3
2
2
-1
2
3
2
2
x
2 nx;2 n ;2 ;n0
x
15.
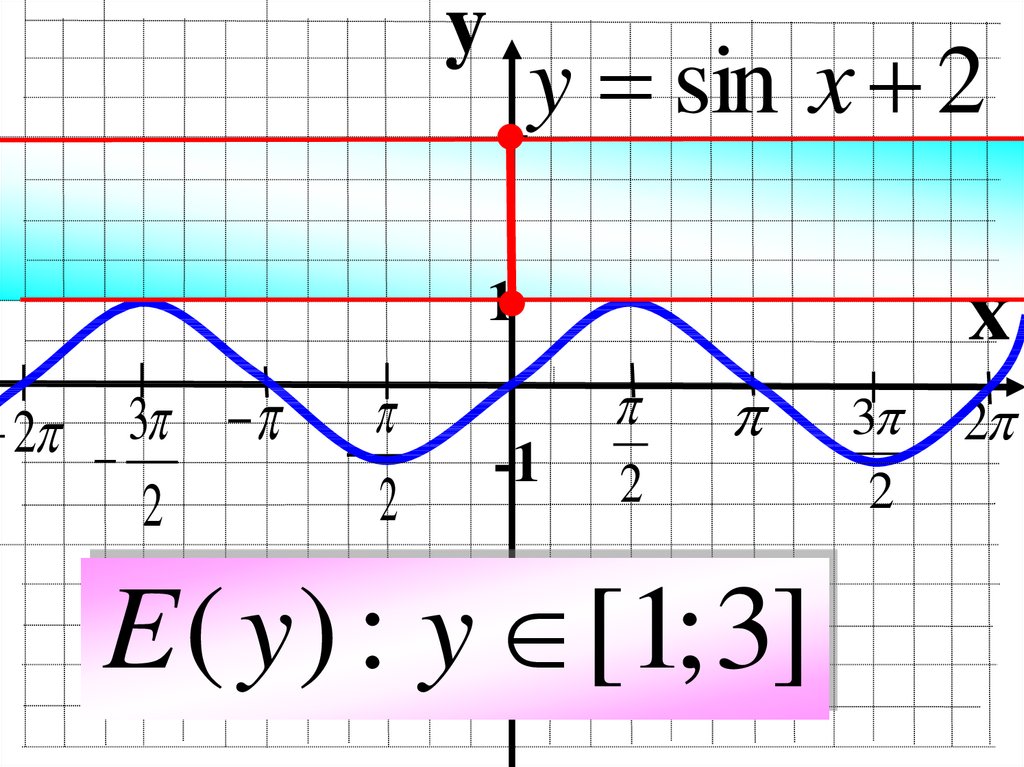
yy = sin x 2
x
1
2 3
2
2
-1
2
E ( y ) : y [1; 3]
3
2
2
16.
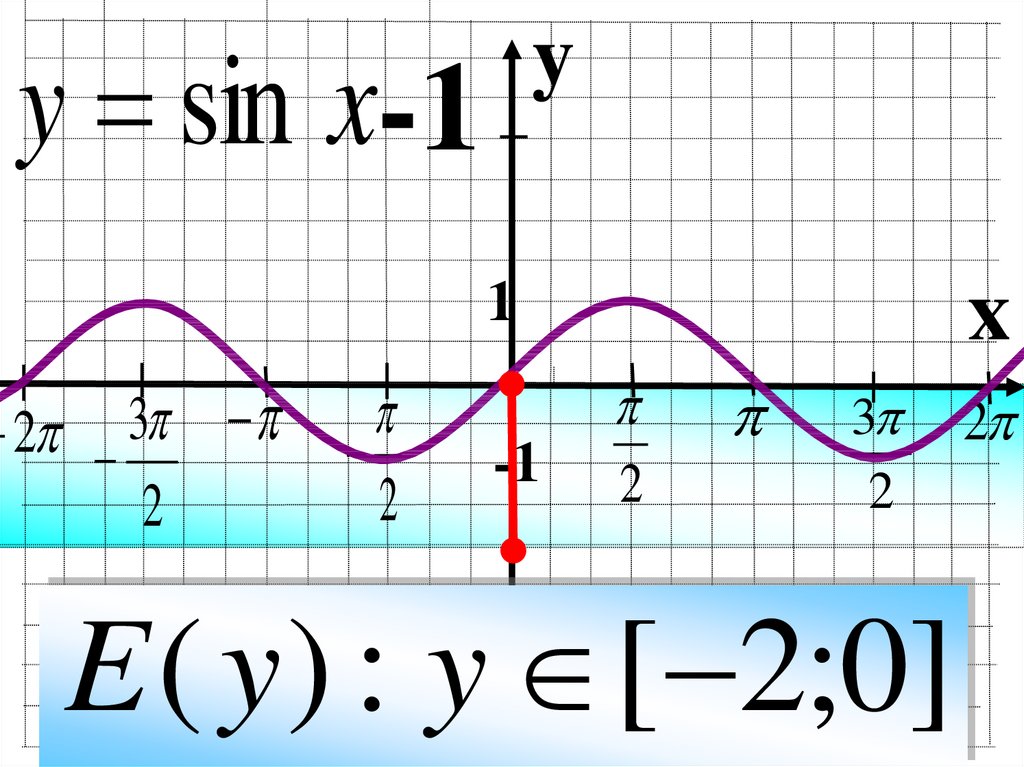
y = sin x-1y
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [ 2;0]
2
17.
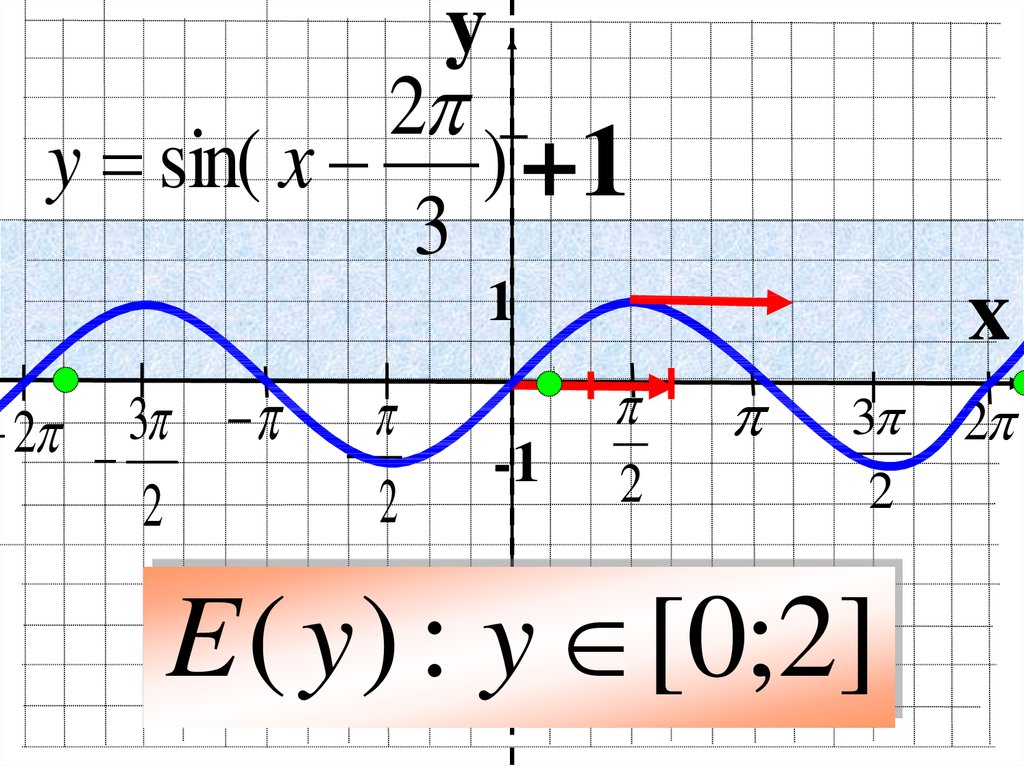
y2
y = sin( x ) +1
3
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [0;2]
2
18.
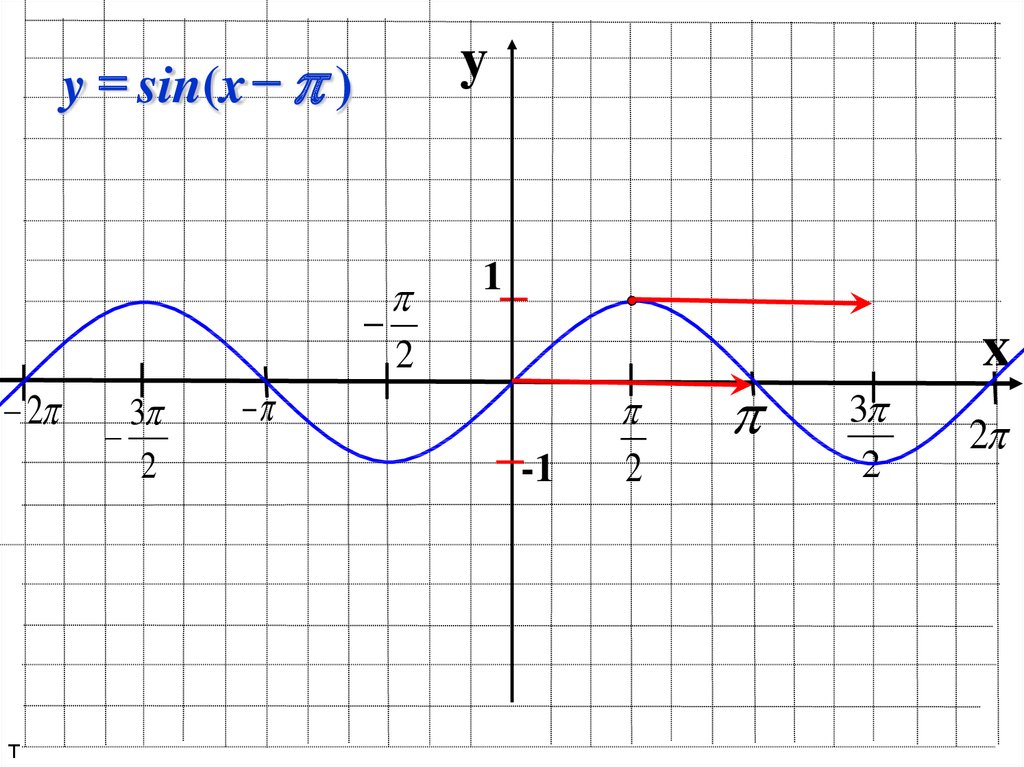
y = sin(x )y
2
2
т
3
2
1
-1
2
x
3
2
2
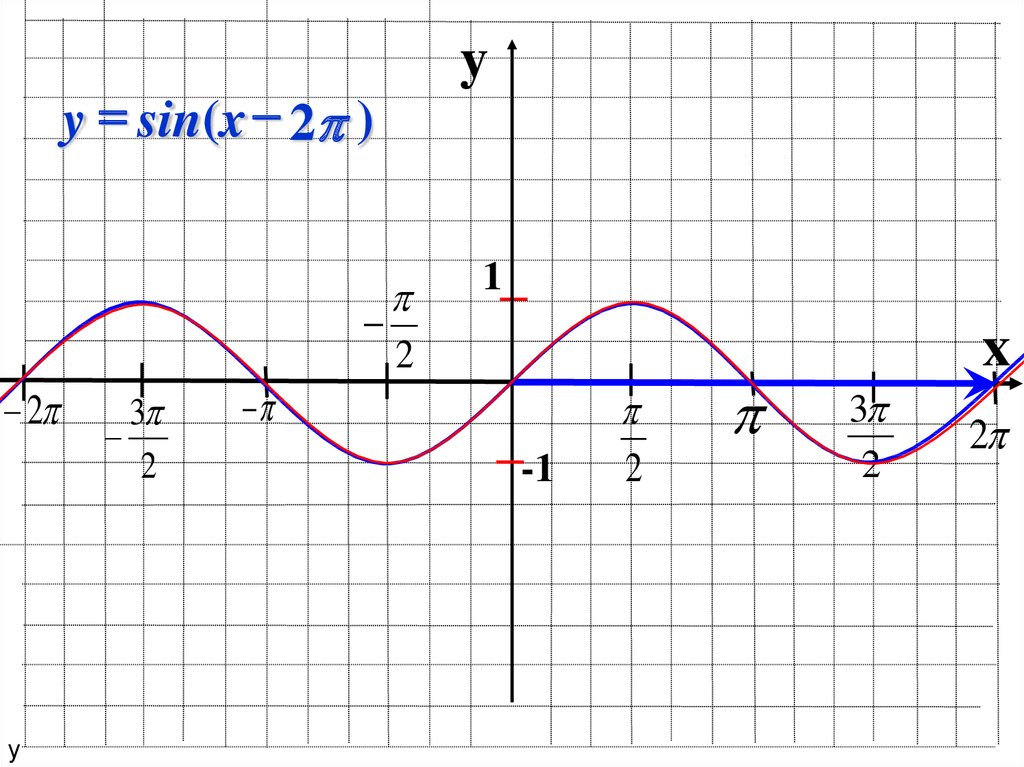
19.
y = sin(x 2 )2
2
у
3
2
y
1
-1
2
x
3
2
2
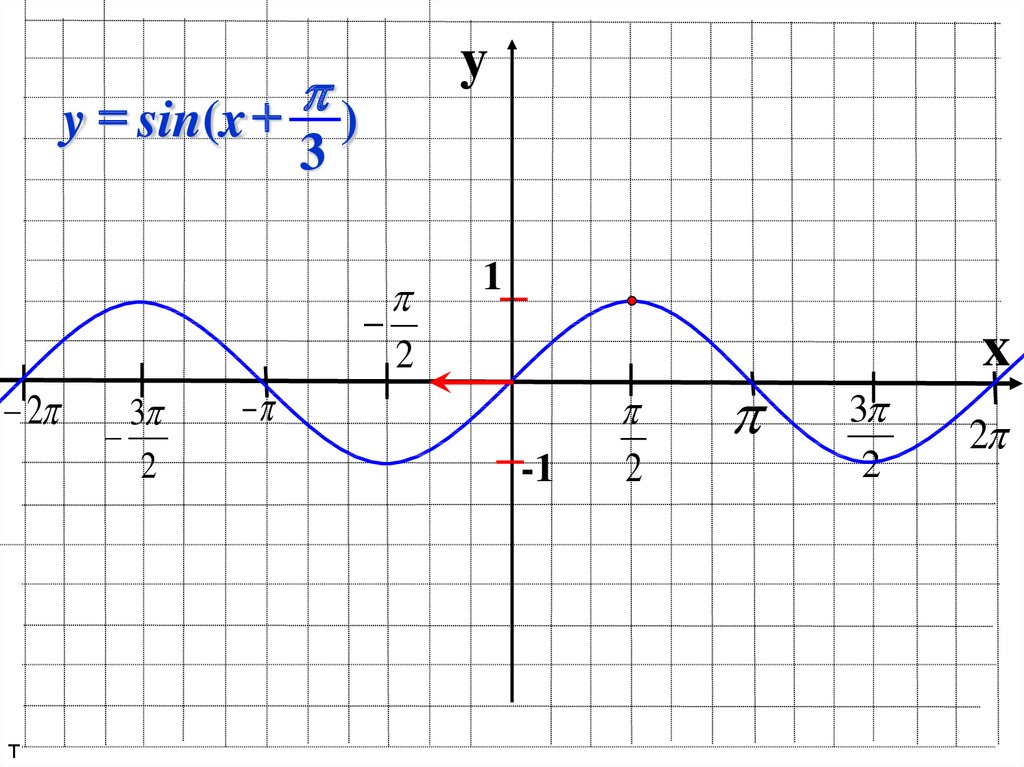
20.
yy = sin(x )
3
2
2
т
3
2
1
-1
2
x
3
2
2
21.
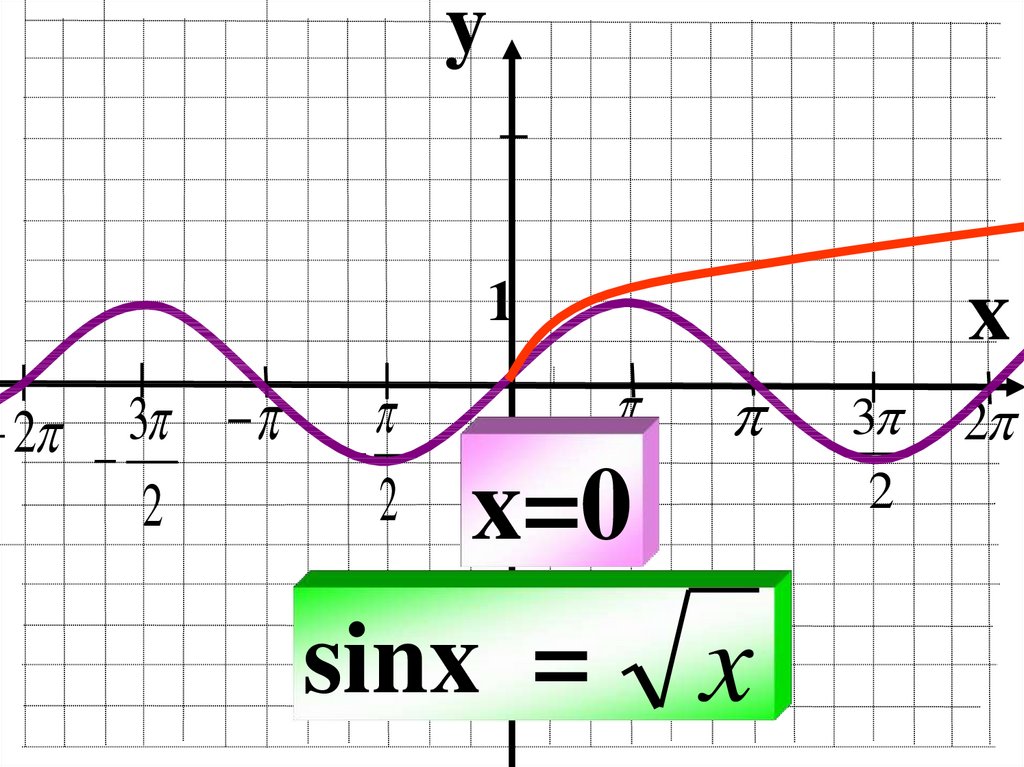
22.
2 32
y
x
1
2
-1
2
x=0
sinx = x
3
2
2
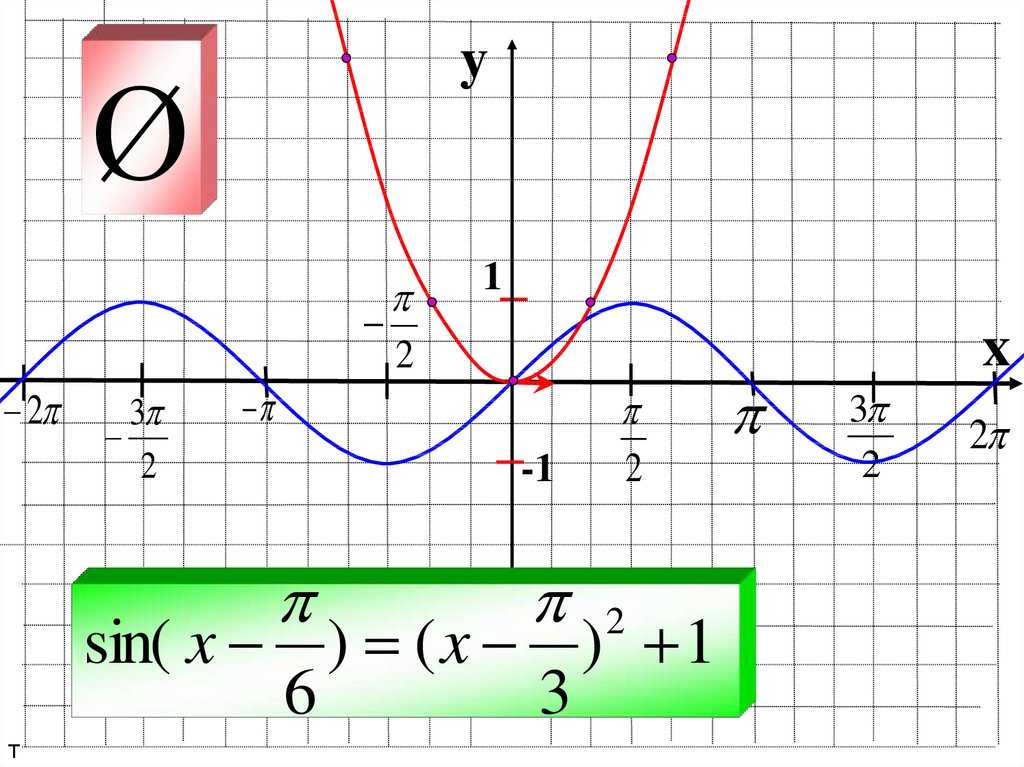
23.
yØ
2
2
3
2
1
-1
2
sin( x ) = ( x ) 1
6
3
т
2
x
3
2
2
24.
yØ
2 3
2
x
1
2
-1
sinx >
2
3
2
x +1
2
25.
yy = sin x
y = x 1
x [0; )
x
1
2 3
2
2
-1
sinx <
у
2
3
2
x +1
2
26.
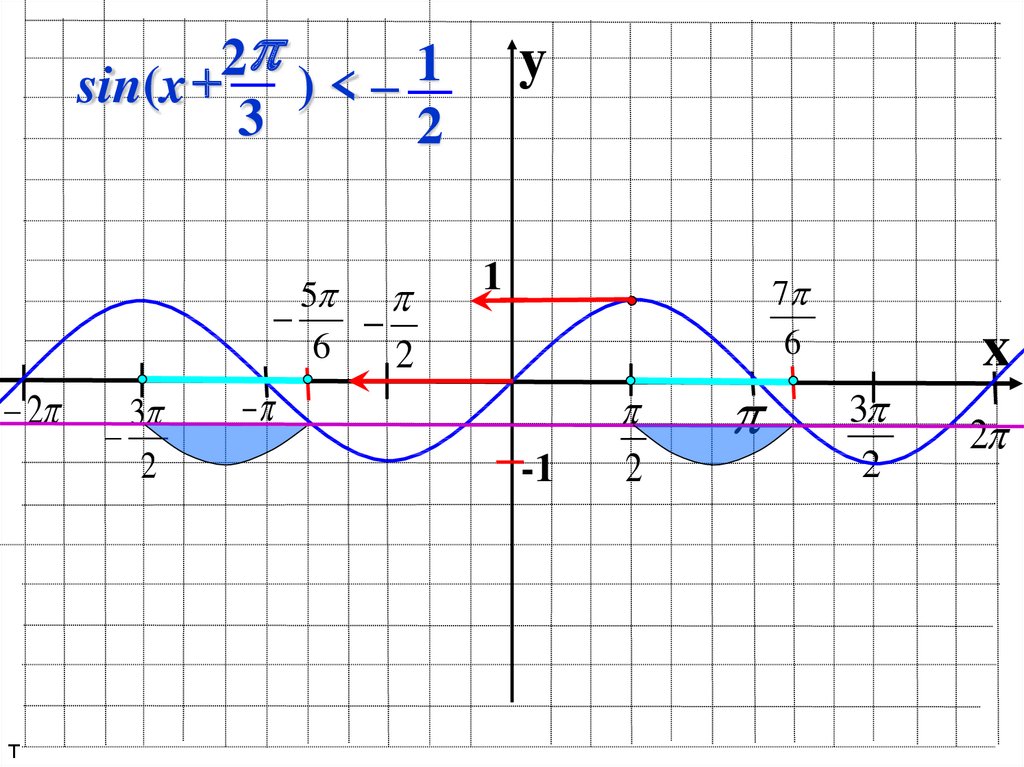
21
sin(x
)<–
3
2
5
6
2
2
т
3
2
y
1
7
6
-1
2
x
3
2
2
27.
yI
I
3
2
2
I
I
-1
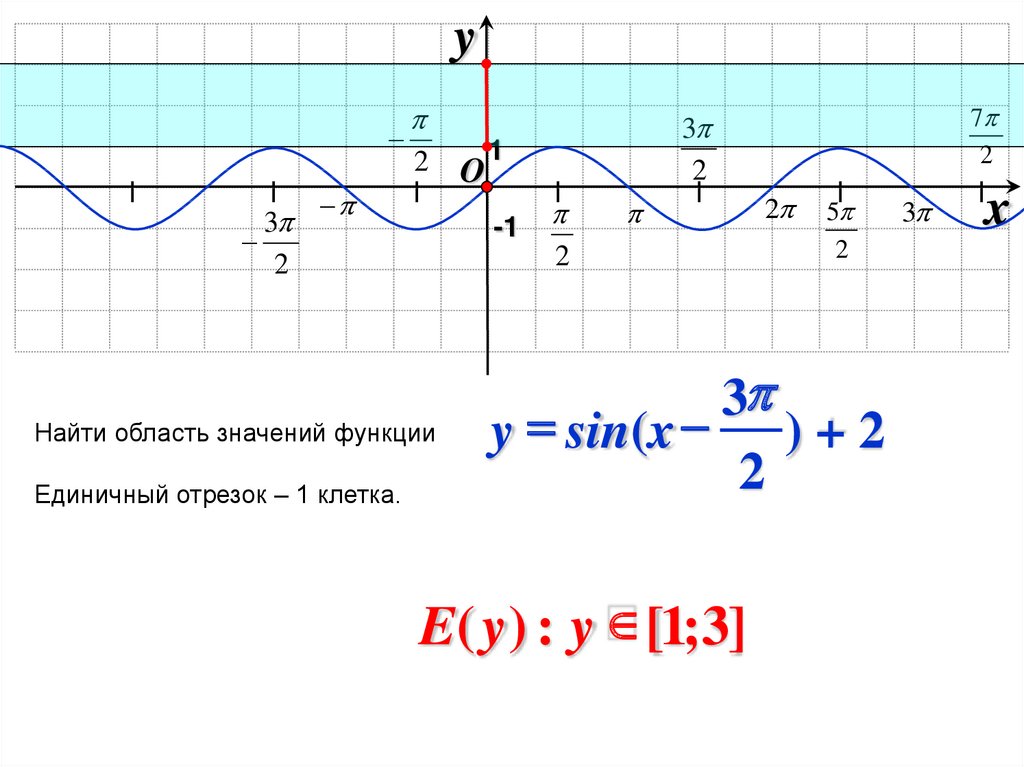
Найти область значений функции
Единичный отрезок – 1 клетка.
O
1
2
3
2
I
7
2
2
I
5
2
3
y = sin(x ) + 2
2
E( y ) : y [1;3]
3
I
x
28.
Умение строить графики нам нужны при …решении уравнений;
решении неравенств;
решении заданий, связанных с исследованием
свойств функций.
Рассмотрим графики функций, аналитическая запись
которых содержит знак абсолютной величины.
29.
y = sin x2 3
2
y
x
1
2
-1
2
3
2
2
30.
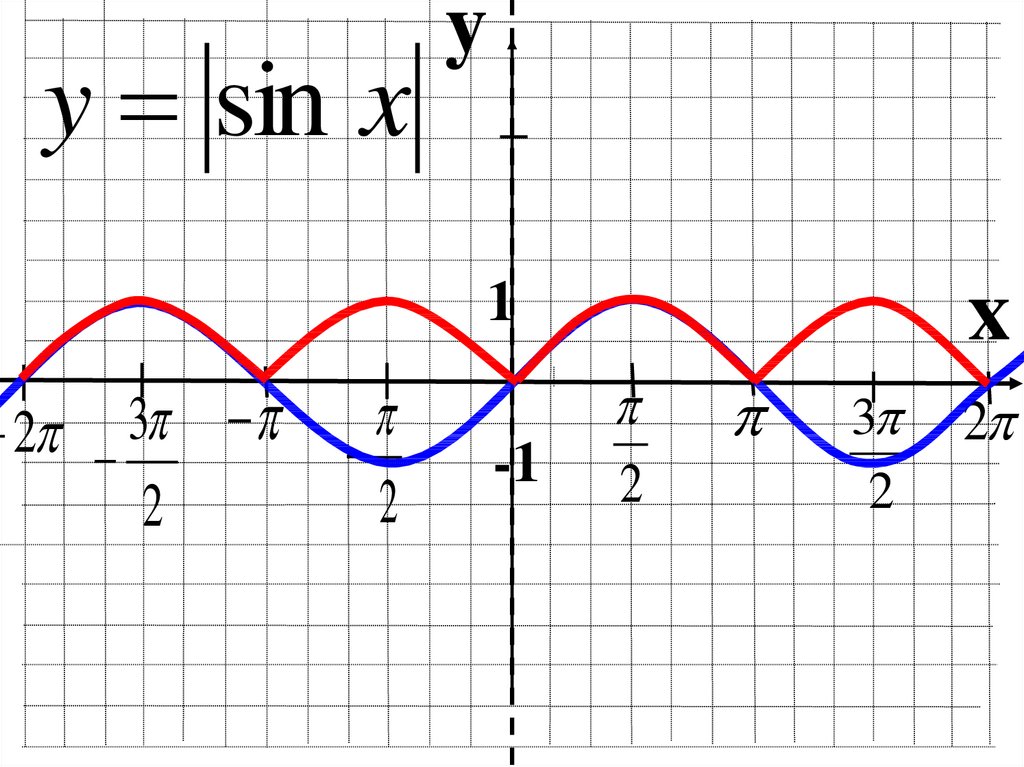
yy = sin x
2 3
2
x
1
2
-1
2
3
2
2















 Математика
Математика








