Функция y=sinx

1.

Функция y=sinx

2. Содержание

Построение графика у =sinx
Свойства функции у =sinх
Сдвиг вдоль оси абсцисс
Сдвиг вдоль оси ординат
Симметрия относительно оси абсцисс
Сжатие и растяжение к оси ОХ
Сжатие и растяжение к оси ОУ
График у = ∣sinx∣

3.

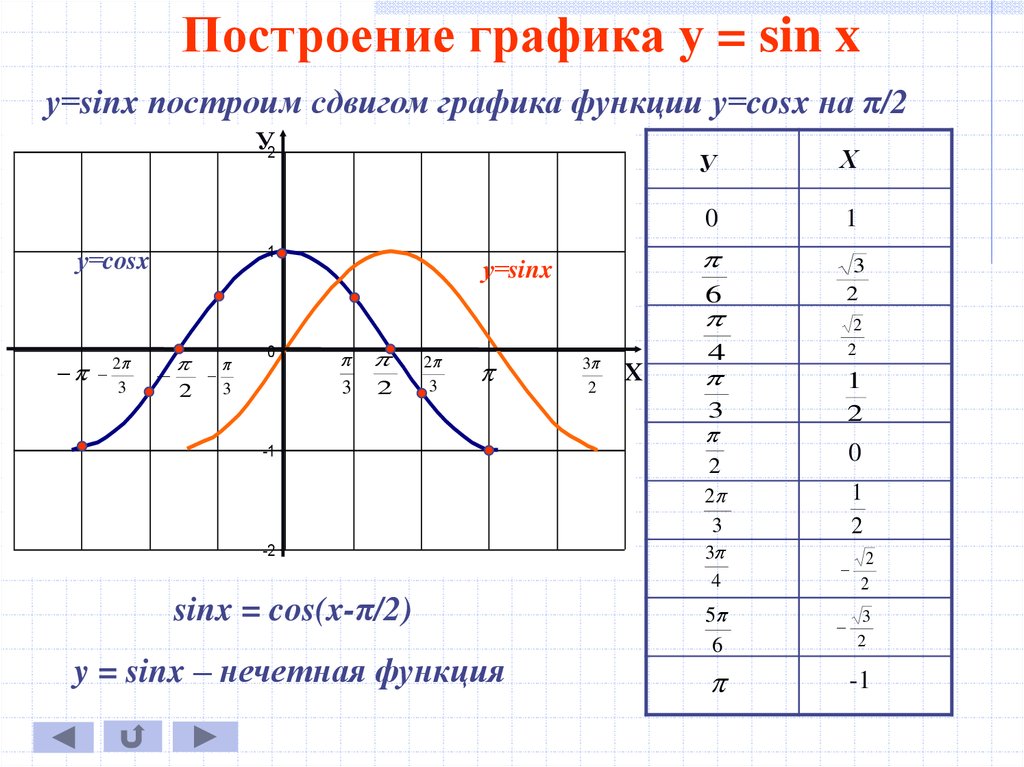
Построение графика у = sin x
у=sinx построим сдвигом графика функции у=cosx на π/2
У2
1
у=cosx
У
Х
0
1
у=sinx
6
3
2
4
2
2
2
3
2
0
3
3
2
2
3
-1
-2
3
2
Х
3
2
2
3
3
4
sinx = cos(x-π/2)
y = sinx – нечетная функция
1
2
5
6
0
1
2
2
2
3
2
-1

4.

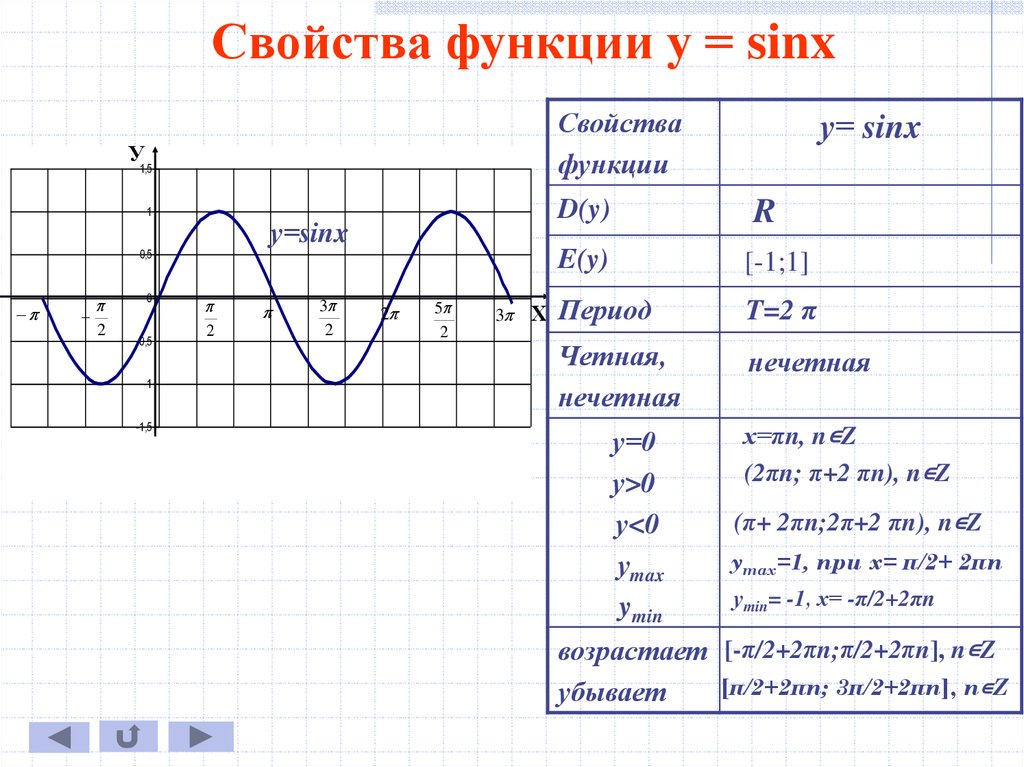
Свойства функции у = sinx
Свойства
функции
У
1,5
1
у=sinx
0,5
2
0
-0,5
-1
-1,5
D(y)
2
3
2
2
5
2
3
Х
у= sinx
R
E(y)
[-1;1]
Период
T=2 π
Четная,
нечетная
нечетная
у=0
у>0
у<0
уmax
ymin
х=πn, n∊Z
(2πn; π+2 πn), n∊Z
(π+ 2πn;2π+2 πn), n∊Z
уmax=1, при х= π/2+ 2πn
уmin= -1, х= -π/2+2πn
возрастает [-π/2+2πn;π/2+2πn], n∊Z
[π/2+2πn; 3π/2+2πn], n∊Z
убывает

5.

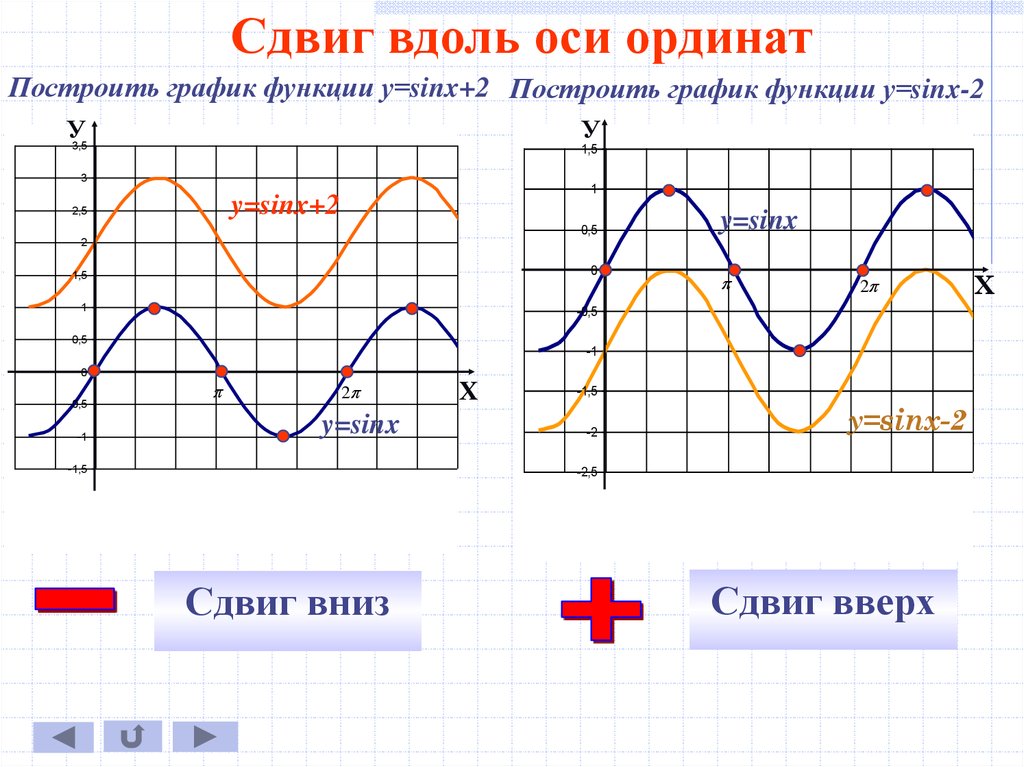
Сдвиг вдоль оси ординат
Построить график функции у=sinx+2 Построить график функции у=sinx-2
У
3,5
У
1,5
3
1
y=sinx+2
2,5
0,5
2
1,5
0
1
-0,5
0,5
0
-0,5
-1
y=sinx
2
-1
2
y=sinx
-1,5
Х
-1,5
-2
y=sinx-2
-2,5
Сдвиг вниз
Сдвиг вверх
Х

6.

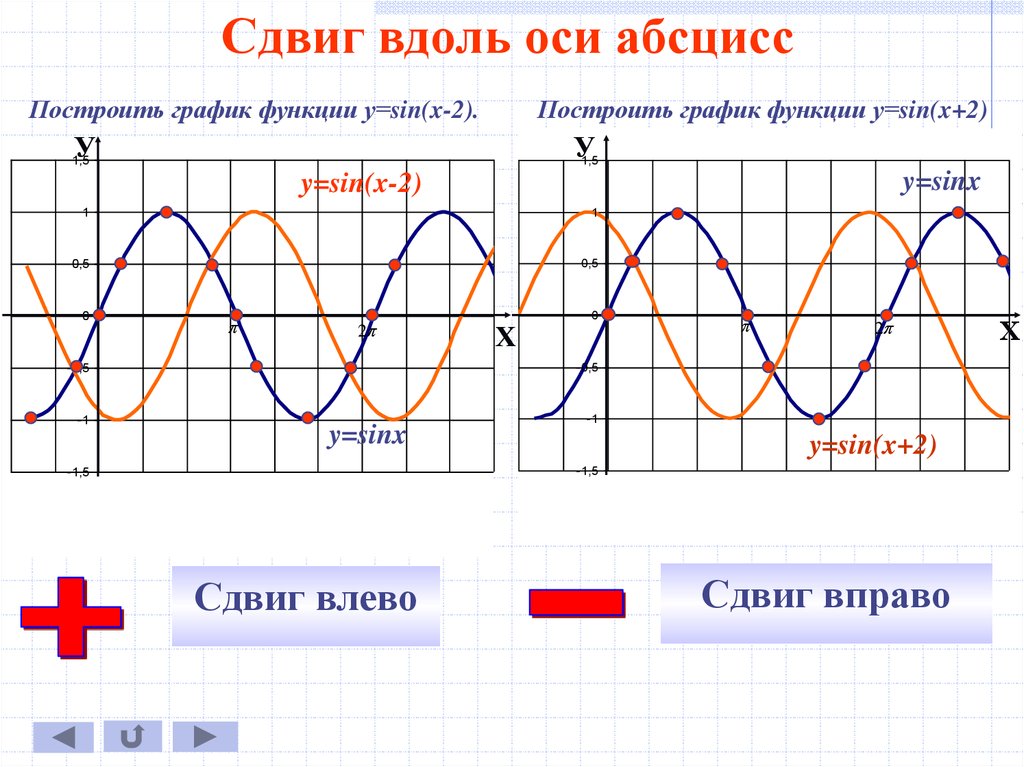
Сдвиг вдоль оси абсцисс
Построить график функции у=sin(x-2).
Построить график функции у=sin(x+2)
У
У1,5
1,5
y=sinx
y=sin(x-2)
1
1
0,5
0,5
0
2
Х
0
-0,5
-0,5
-1
-1
y=sinx
2
y=sin(x+2)
-1,5
-1,5
Сдвиг влево
Сдвиг вправо
Х

7.

Сжатие и растяжение к оси абсцисс y=k∙sinx
Построить график функции у =2sinx
Построить график функции у =1/2sinx
У
У
1,5
2,5
2
1
1,5
1
y=sinx
0,5
2
0
-0,5
2
-1
-1,5
3
2
y=sinx
0,5
5
2
Х
2
0
-0,5
2
5
2
y=2sinx
-1
-2
-2,5
k>1
3
2
Х
y=1/2sinx
-1,5
Растяжение
0<k<1
Сжатие

8.

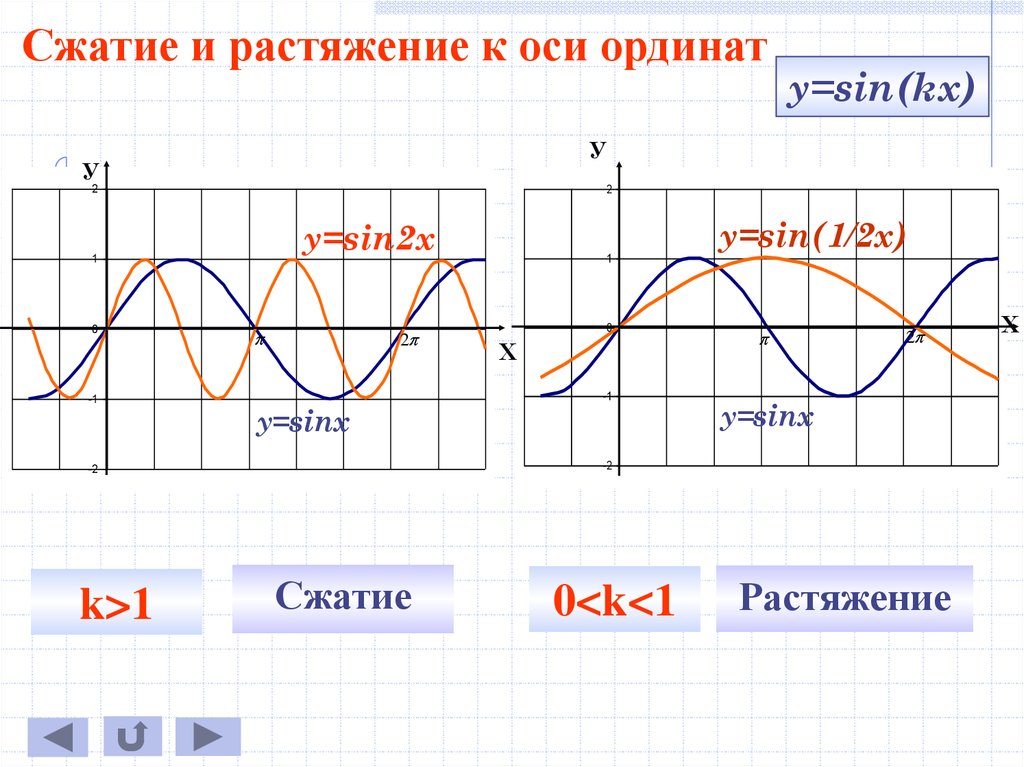
Сжатие и растяжение к оси ординат
У
У
2
2
y=sin2x
1
0
-1
2
1
0
Х
-1
y=sinx
y=sin(1/2x)
2
y=sinx
-2
-2
k>1
y=sin(kx)
Сжатие
0<k<1
Растяжение
Х

9.

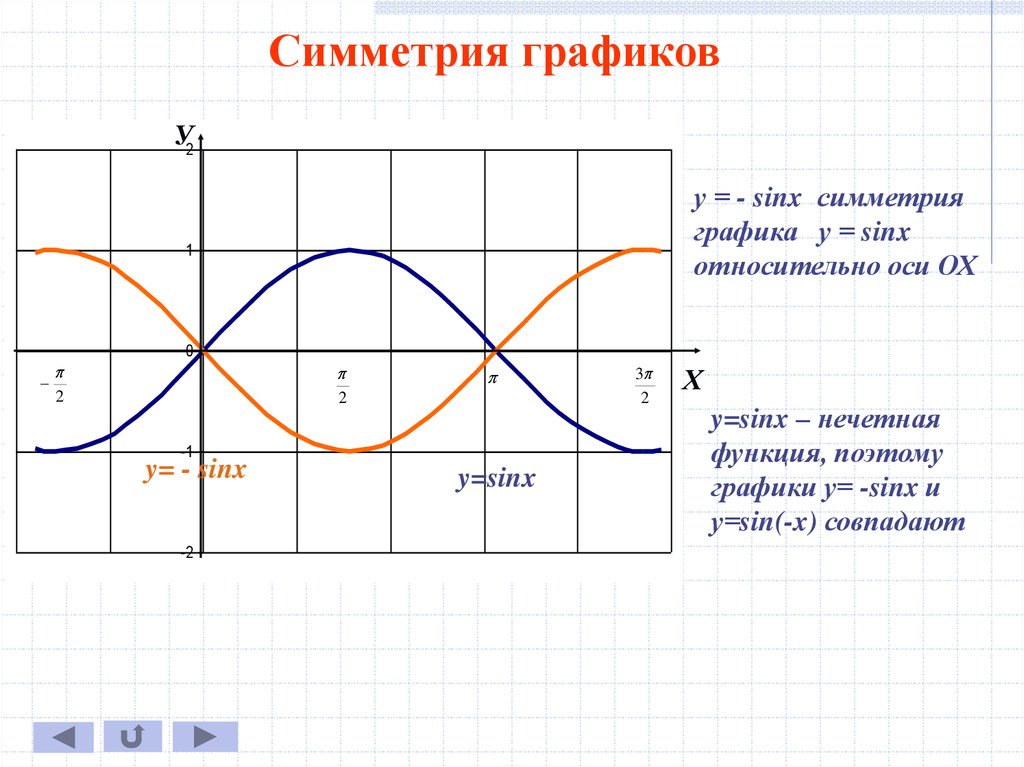
Симметрия графиков
У2
у = - sinx симметрия
графика у = sinx
относительно оси ОХ
1
0
2
2
-1
y= - sinx
-2
y=sinx
3
2
Х
y=sinx – нечетная
функция, поэтому
графики у= -sinx и
у=sin(-x) совпадают

10.

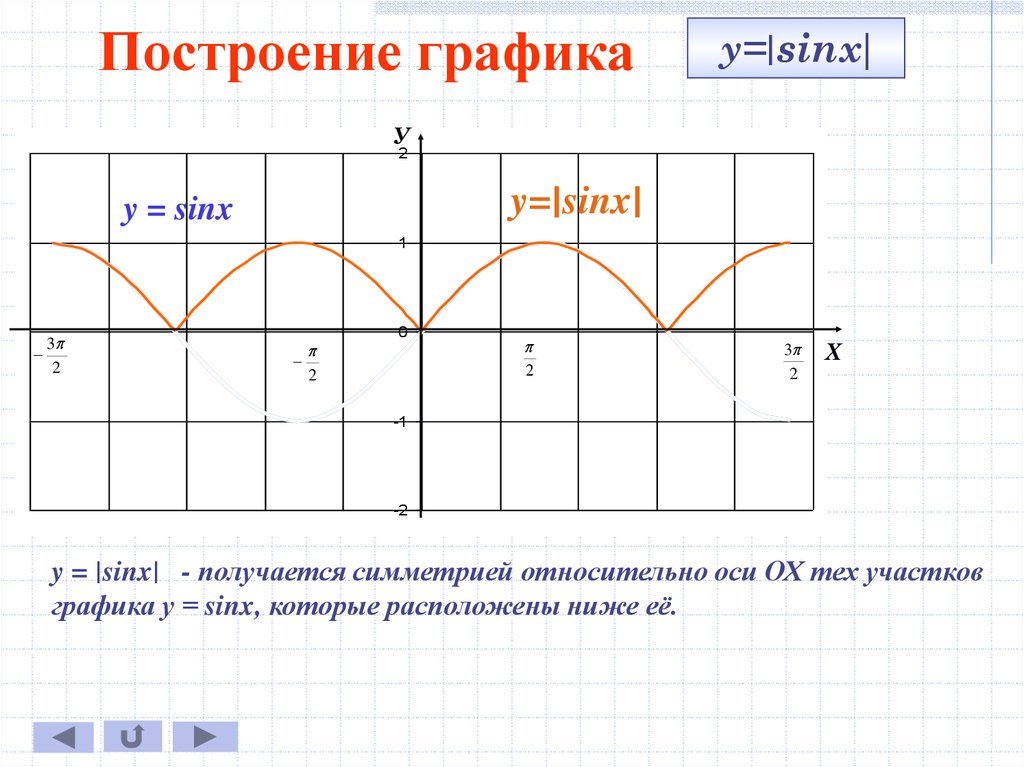
Построение графика
y=∣sinx∣
У
2
y=∣sinx∣
y = sinx
1
3
2
0
2
2
3
2
Х
-1
-2
y = ∣sinx∣ - получается симметрией относительно оси ОХ тех участков
графика у = sinx, которые расположены ниже её.

11.

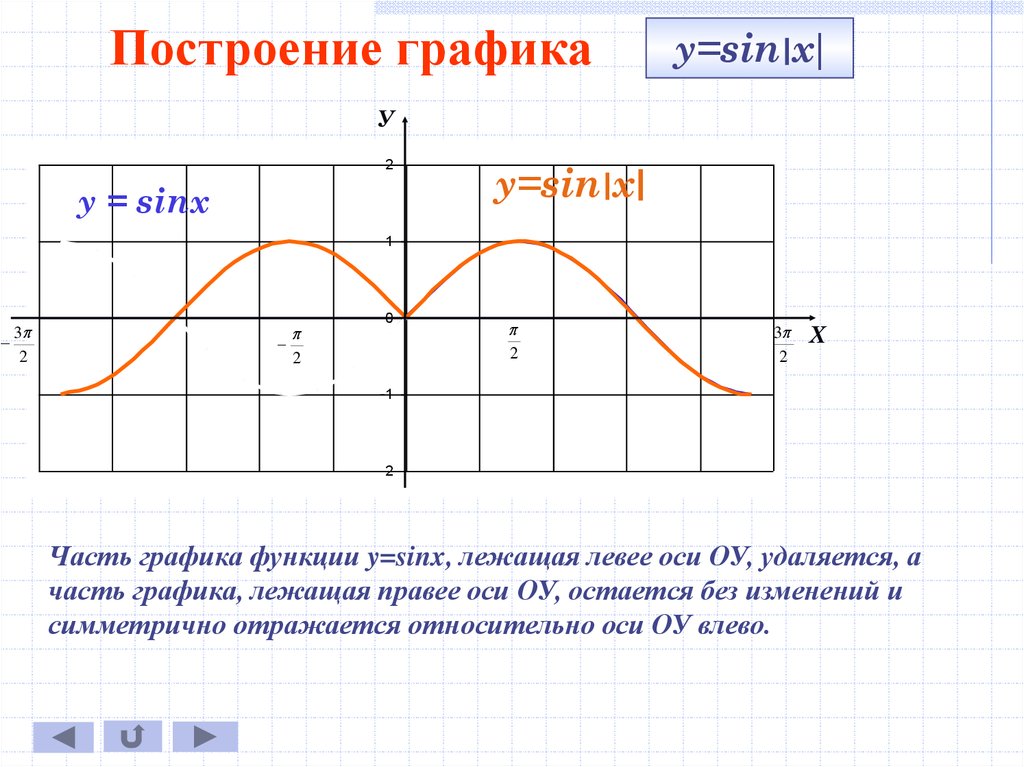
Построение графика
y=sin∣x∣
У
2
y = sinx
y=sin∣x∣
1
3
2
0
2
2
3
2
Х
-1
-2
Часть графика функции y=sinx, лежащая левее оси ОУ, удаляется, а
часть графика, лежащая правее оси ОУ, остается без изменений и
симметрично отражается относительно оси ОУ влево.

12.

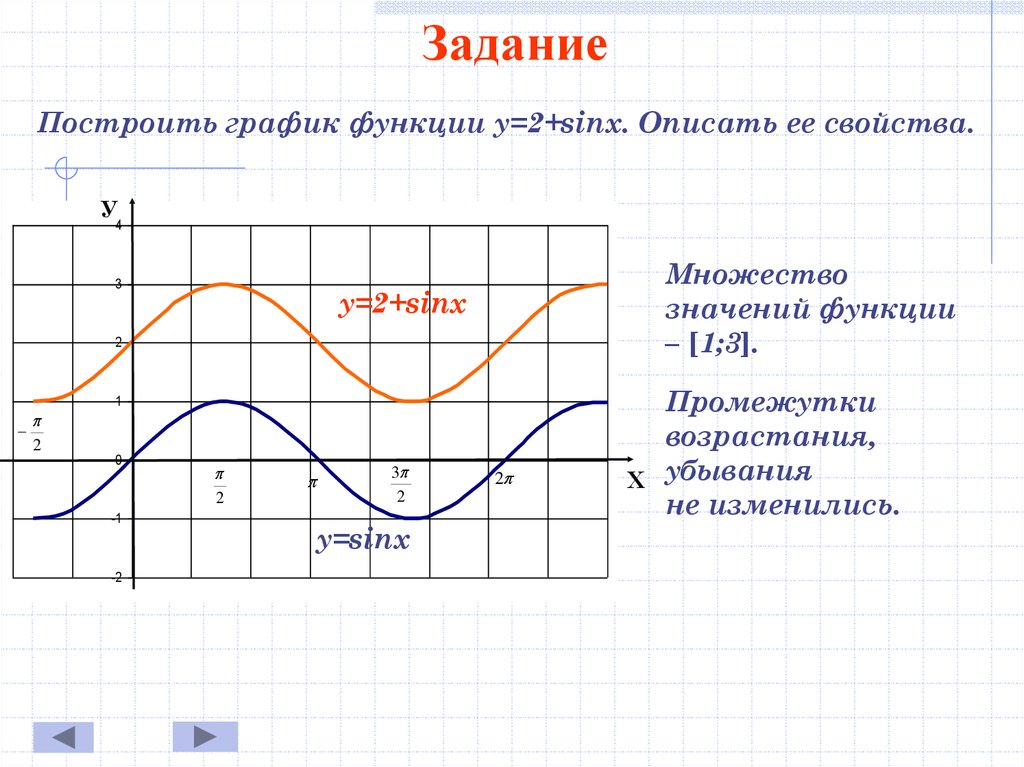
Задание
Построить график функции у=2+sinx. Описать ее свойства.
У
4
3
Множество
значений функции
– [1;3].
y=2+sinx
2
2
1
0
-1
-2
2
3
2
y=sinx
2
Х
Промежутки
возрастания,
убывания
не изменились.

13.

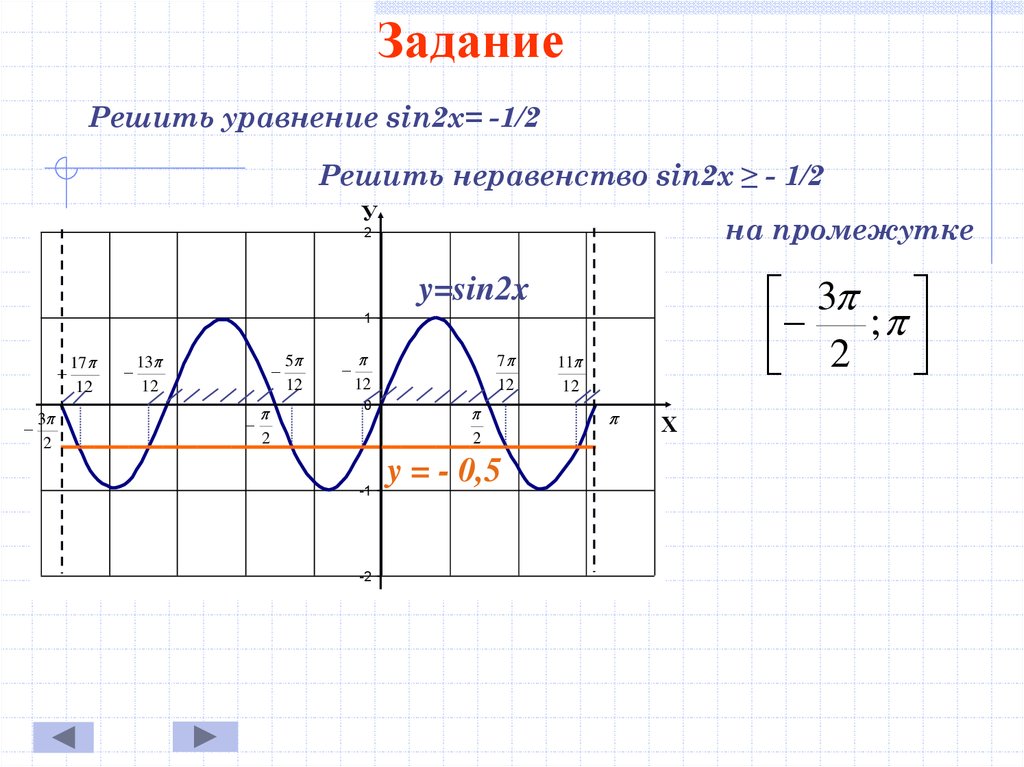
Задание
Решить уравнение sin2x= -1/2
Решить неравенство sin2x ≥ - 1/2
У
на промежутке
2
3
2 ;
y=sin2x
1
3
2
17
12
13
12
5
12
7
12
12
0
2
-1
-2
2
y = - 0,5
11
12
Х

14.

Литература
Ш.А.Алимов, Ю.М.Колягин и др. «Алгебра и начала анализа 10-11»:
М. «Просвещение» 2003.
Н.Е.Федорова, М.В. Ткачева «Изучение алгебры и начала анализа 1011»: М. «Просвещение» 2004.