Похожие презентации:
Дифференциальные уравнения
1.
Дифференциальные уравненияУравнение, связывающее искомую функцию
одной или нескольких переменных, эти
переменные и производные различных
порядков данной функции, называется
дифференциальным уравнением. Например:
y 6 x;
y 10 3x.
2.
Если искомая функция зависит от однойпеременной, то дифференциальное уравнение называется обыкновенным, если от нескольких – то уравнением в частных
производных.
В общем случае дифференциальное уравнение можно записать в виде
G( x, y, y ,..., y ) 0,
n
3.
где G - некоторая функция от n 2переменных, при этом порядок n старшей
производной, входящей в запись уравнения,
называется порядком дифференциального
уравнения.
Решением дифуравнения называется такая
функция y y (x ) , которая при подстановке
ее в это уравнение обращает его в
тождество.
4.
Задача о нахождении решения некоторогодифференциального уравнения называется
задачей интегрирования дифференциального
уравнения. График решения диффуравнения
называется интегральной кривой.
Общим решением дифференциального
уравнения п - го порядка называется такое
y ( x, C1 ,..., Cn ),
его решение:
которое является функцией переменной х и n
произвольных независимых постоянных
С1, С2, ..., Сn.
5.
Частным решением дифференциальногоуравнения называется уравнение, получаемое
из общего решения при некоторых конкретных
числовых значениях постоянных С1, С2, ..., Сn.
3
В приведенном примере
y x C1 x C2
3
общее решение,
y x 2x 1
частное решение уравнения.
6.
Дифференциальные уравнения первогопорядка
Такие уравнения имеют вид: y f ( x, y ),
где f ( x, y ) - функция двух переменных,
определенная на плоскости ОХУ.
Методы решения таких переменных:
y f (x). Его можно
1. Уравнение
представить в виде dy f ( x)dx.
Интегрируя, получим решение
y f ( x)dx.
7.
2. Уравнениеy f ( y ). Ищем решение в
виде x x( y ), т.е. считаем, что переменная
y обозначает независимую переменную, а
переменная x - функцию. Поскольку
y dy / dx, то уравнение можно записать в
виде
dy / f ( x) dx. x
dy
.
f ( y)
8.
3. Если дифференциальное уравнение имеетвид
1 dy
то (ln y ) f ( x), и,
y dx
f ( x),
интегрируя, получаем:
откуда
f ( x ) dx C
y e
.
ln y f ( x)dx C ,
Пример. Решить уравнение
y (3 2 x)dx xdy 0.
9.
1 dy 3 2 x,
Имеем xdy y (3 2 x)dx
y dx
x
1 dy 3
2, откуда
или
y dx x
3
ln y ( 2)dx C ln y 3 ln x 2 x C.
x
Выполнив преобразования, получим
y
ln y ln x 2 x C ln 3 2 x C.
x
3
Окончательно
3 2 x C
y x e
.
10.
Дифференциальное уравнение первогопорядка называется уравнением с разделяющимися переменными, если оно может быть
представлено в виде:
dy
f ( x)h( y ),
dx
где
f ( x), h( y ) функции переменных x, y.
Для решения такого уравнения его приводят
к виду
dy
f ( x)d ( x)
h( y )
dy
f ( x)d ( x).
h( y )
11.
Однородные дифференциальныеуравнения первого порядка
Дифференциальное уравнение первого
порядка называется однородным, если оно
может быть представлено в виде, когда в
левой части уравнения находится производная,
а правая часть есть функция частного у/х:
y f ( y / x).
Основной метод решения таких уравнений –
это введение в рассмотрение вспомогательной
функции и = у/х, что позволяет свести это
уравнение к уравнению с разделяющимися
переменными.
12.
Пример. Решить уравнение( y x )dx 2 xydy 0
2
2
2
y
1
2
2
dy y x
dy x
.
y
dx
2 xy
dx
2
x
введя переменную u y / x, имеем
y xu, u u xu .
13.
Выполнив преобразования, в итоге получимy
y
x 2 1 C
x C.
x
x
2
2
Дифференциальное линейное уравнение
первого порядка
Дифференциальное уравнение первого
порядка называется линейным, если оно имеет
вид: y f ( x) y g ( x),
где f ( x ), g ( x )некоторые функции переменной.
В случае, когда функция g (x ) тождественно
равна нулю, уравнение называется однородным. В противном случае - неоднородным.
14.
Пример. Решить уравнение2
3
y y 2 x .
x
Вначале решаем однородное уравнение
2
y 2
2
y y 0. . y Cx ,
x
y x
где С – произвольная постоянная.
2
Теперь возьмем функцию y C ( x) x ,
где C (x ) неизвестная функция.
Определим производную
y C ( x) x C ( x)2 x.
2
15.
Подставляя значенияy, y
в исходное
выражение и произведя преобразования,
получим C ( x) x 2 2 x 3 C ( x) 2 x.
Интегрируя, имеем
C ( x) 2 xdx x A,
2
где А – произвольная постоянная.
Окончательно:
y ( x A) x .
2
2
16.
Дифференциальные уравнения второгопорядка
Дифференциальным линейным уравнением
второго порядка называется уравнение вида:
y h( x) y g ( x) y f ( x),
где h( x), g ( x), f ( x) - функции переменной х.
Если f ( x) 0, то уравнение неоднородное.
Если f ( x ) 0,, то уравнение однородное.
Если функции h( x), g ( x) равны постоянным
коэффициентам а и Ь, то полученные уравнения называются уравнениями с постоянными
коэффициентами.
17.
Дифференциальные уравнениявторого порядка, допускающие понижение
порядка
В некоторых случаях решение дифференциального уравнения второго порядка может
быть сведено к последовательному решению
двух дифференциальных уравнений первого
порядка. В этом случае говорят, что данное
дифференциальное уравнение допускает
понижение порядка. Если дифференциальное
уравнение имеет вид: y f (x),
то оно решается последовательным
интегрированием.
18.
Линейные дифференциальные уравнениявторого порядка с постоянными
коэффициентами
Линейной комбинацией функций y1 ( x), y2 ( x)
с коэффициентами С1 и С2 называется
выражение вида C1 y1 ( x) C2 y2 ( x).
Функции y1 ( x), y2 ( x)
являются линейно
независимыми, если их отношение
y1 ( x) / y2 ( x)
непостоянно. В противном случае функции
y1 ( x), y2 ( x) являются линейно зависимыми.
19.
Для решения линейных уравнений второгопорядка с постоянными коэффициентами
используется следующая теорема. Если
y1 ( x), y2 ( x) - линейно независимые частные
решения линейного дифференциального
уравнения второго порядка с постоянными
коэффициентами вида:
y ay by 0,
то общее решение является линейной
комбинацией этих частных решений:
y C1 y1 C2 y2 .
20.
Если характеристическое уравнениеa b 0
2
имеет действительные корни 1 , 2 , причем
1 2,,тогда общее решение уравнения, имеет
1 x
2 x
вид:
y C1e C2e .
Если характеристическое уравнение имеет
один корень (кратности 2), то общее решение
x
y (C1 C2 x)e .
уравнения имеет вид:
Если характеристическое уравнение не имеет
действительных корней, то общее решение
уравнения имеет вид:
x
x
y C1e sin x C
cos x,
2 2e
a
a
где , b .
некоторые числа
2
4
21.
2где
a
a
, b .
2
4
Метод Рунге – Кутта
Связь между соседними значениями функции
x h
дает равенство:
y ( x h) y ( x )
y
(
t
)
dt
x
Приближенное значение интеграла вычисляется численными методами.
Для применения метода используется общий
подход. Фиксируют некоторые числа:
22.
2 ,..., q ; p1 ,..., pq ; ij ,0 j i q.Последовательно вычисляют:
k1 (h) hf ( x, y),
k2 (h) hf ( x 2h, y 12k1 (h)),
……..
k q (h) hf ( x q h, y q1k1 (h) ... qq k q 1 (h))
и полагаем
q
y( x h) y( x) pi ki (h) z (h).
i 1
23.
Рассмотрим вопрос о выборе параметровi , pi , ij .
Пусть
(h) y ( x h) z (h).
Предполагаем, что (0) (0) ... ( s ) (0) 0,
( s 1)
(0) 0 для некоторой функции f ( x, y ).
а
По формуле Тэйлора имеем:
s
(h)
(0)
i 0
где
0 1.
(i )
i!
( s 1)
( h) s 1
h
h ,
( s 1)!
i
24.
При q 1 Имеем:(h) y( x h) y( x) p1hf ( x, y),
(0) 0,
(0) ( y ( x h) p1 f ( x, y)) h 0 f ( x, y)(1 p1 ),
(h) y ( x h).
Погрешность на шаге:
2
( x h)h
( h)
.
2
25.
На практике наиболее часто используютq 4, s 4.
метод Рунге-Кутта с
В этом случае расчетные формулы:
k1 hf ( x, y),
h
k1
k 2 hf ( x , y ),
2
2
h
k2
k3 hf ( x , y ), k4 hf ( x h, y k3 ),
2
2
1
y z (h) y ( x) (k1 2k 2 2k3 k 4 ).
6
26.
Погрешность рассмотренного методаРунге-Кутта на шаге пропорциональна пятой
степени шага.
Пример. Методом Рунге-Кутта найти решение
задачи Коши для уравнения
y y x 2 , y(1) 0, x 1,2 ,
в первых пяти точках, взяв h 0,1.
2
Т.к. x0 1, y0 0, f ( x, y ) y x ,
поэтому
f x0 , y0 y0 x 0 1 1.
2
0
27.
Далее находим:k h f x0 , y0 0,1 1 0,1;
1
1
k 0,1 f 1,05; 0,05 0,1 [ 0,05 1,05 ] 0,1152;
2
1
2
k 0,1 f 1,05; 0,0576 0,1 [ 0,0576 1,05 ] 0,1160;
2
1
3
k 0,1 f 1,1; 0,1160 0,1 [ 0,1160 1,1 ] 0,1326.
1
4
2
Вычислим
1
y0 0,1 2 0,1152 2 0,1160 0,1326 0,1158
6
28.
и далееy1 y0 y0 0 0,1158 0,1158.
Таким образом, получено приближенное
значение решения при x1 x0 h 1,1,
а именно y1 0,1158.
Аналогично находим y2 , y3 , y4 , y5 .























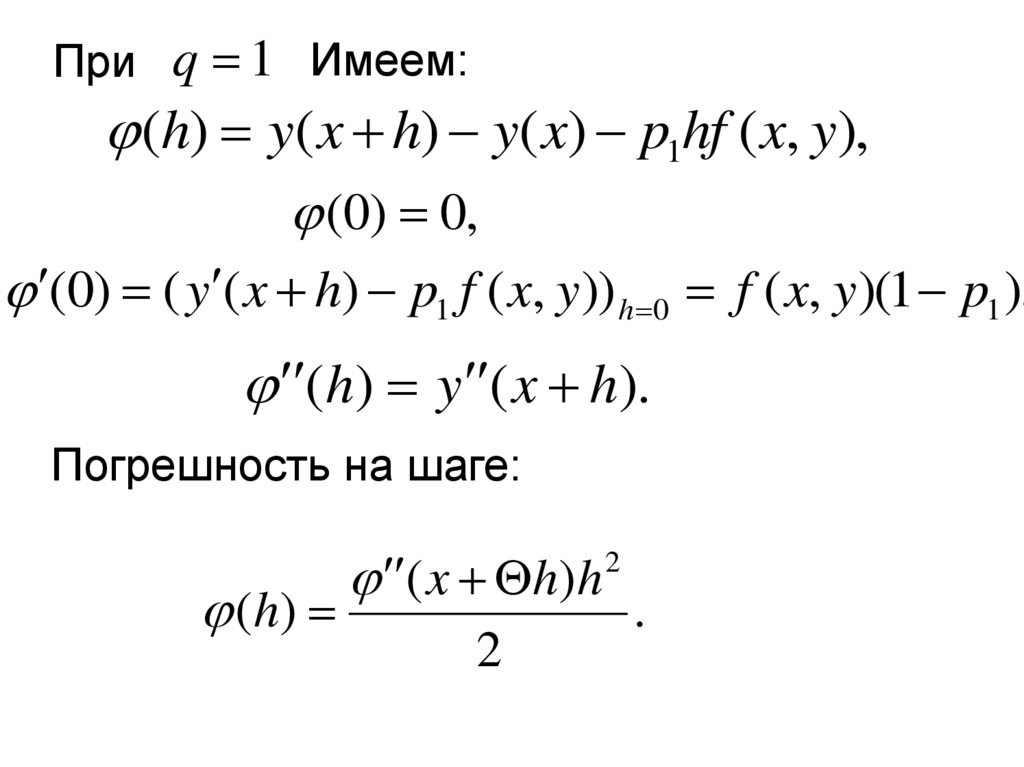




 Математика
Математика








