Показатели надежности. Закон Вейбула. Закон распределения плотностью

1.

Таблица 1 - Функциональные связи между основными показателями
надежности
Показатели
Q (t )
P( t )
Q (t )
1 P (t )
Q (t )
f (t )
t
f ( x )dx
0
R(t )
1 Q(t )
P( t )
f ( x )dx
t
f (t )
d
Q (t )
dt
( t )
d
F (t )
dt
1 F (t )
d
P (t )
dt
d
ln P(t )
dt
f (t )
( t )
t
1 ехр ( x )dx
0
t
ехр ( x )dx
0
t
(t ) ехр ( x )dx
0
f (t )
t
f ( x )dx
( t )

2.

Таблица 2 - Выражения для расчета показателей надежности
по известным функциям распределения
Закон распределения
с плотностью f (t)
Экспоненциальный
f t exp t , t 0
Тср
Выражение для расчета
Интенсивность
Вероятность
безотказной работы P(t) отказов (t)
1/λ
exp(-λt)
Г (1 1/ )
t
exp
1
t
1
t
Ф
2
f t
P t
2
exp
2
1
ln( t )
Ф
2
f t
P t
x
x 1
exp
Г ( ) dx
t
f t
P t
Вейбулла
t
f t t 1 exp , t 0
Нормальный
t 2
f (t )
exp
2
2
2
1
Логарифмический
нормальный
f (t )
ln( t )
exp
2 2
2
2
1
, t 0
Гамма
1
t
f (t )
exp , t 0
Г ( )
t

3.

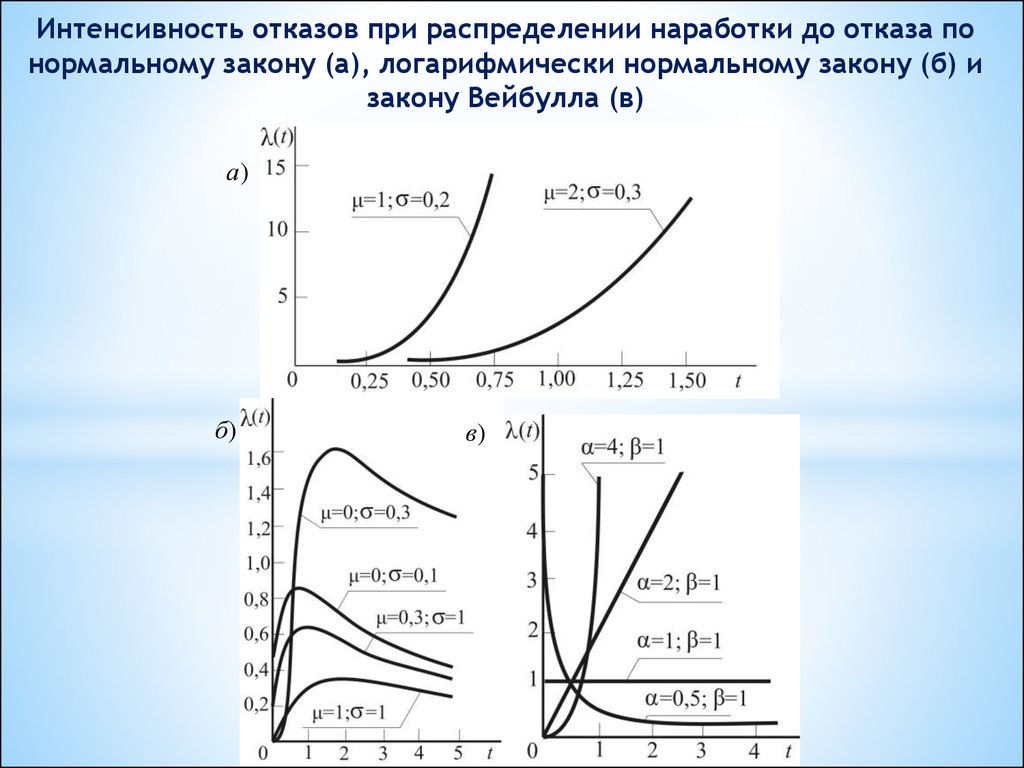
Интенсивность отказов при распределении наработки до отказа по
нормальному закону (а), логарифмически нормальному закону (б) и
закону Вейбулла (в)
а)
б)
в)

4.

Модели процессов нагрузка–прочность
М( ) – математическое ожидание характеристики прочности;
М( ) – математическое ожидание характеристики нагруженности

5.

Схематизация процессов нагруженности и прочности

6.

К определению условия прочности (а) и
условия достижения предельного состояния (б)

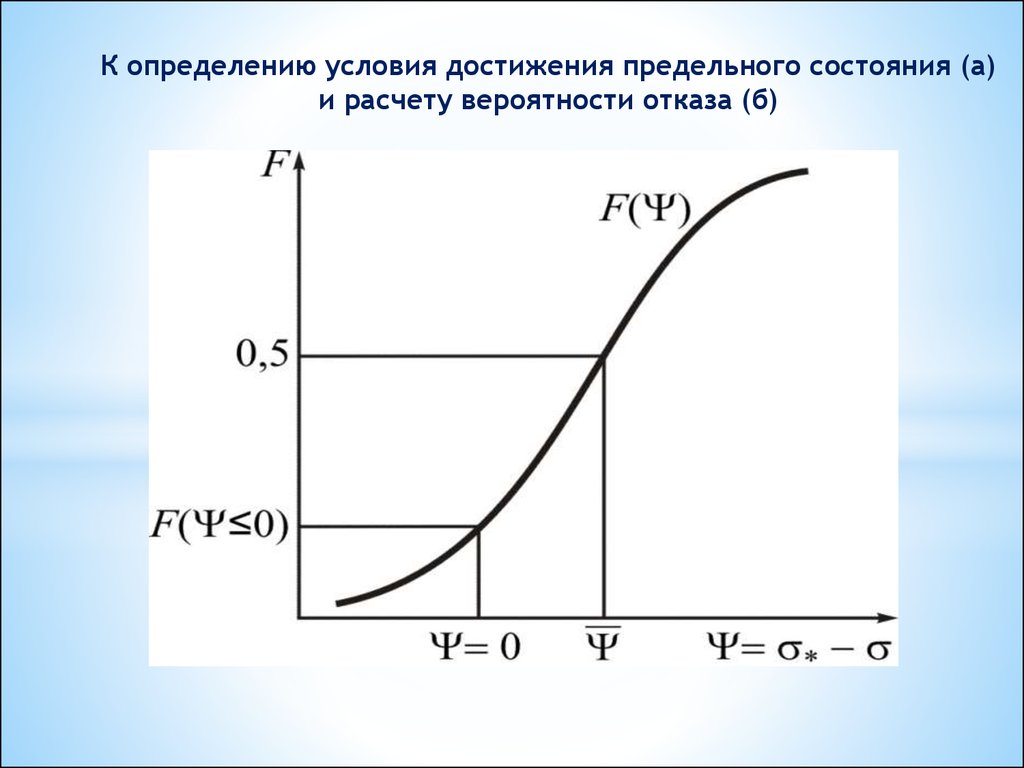
7.

К определению условия достижения предельного состояния (а)
и расчету вероятности отказа (б)