Похожие презентации:
Правила дифференцирования. Производная функции
1. Производная функции .
Как вычислитьпроизводную?
Как найти значение
производной в указанной
точке?
2.
хр
1) х х
1
2
m
n
2) х x
1
1
3) х х ;
4) х n х
1
5)
1
n xm
m
n
n
x
mn
3.
1.(u v) u v2.(u v) u v
3.(u v) u v u v
4.(c u) c u , где с-число.
u
u
v
u
v
5.(
)
v
v2
4. №1.
а) у х 3х х 58
4
у х 3х х 5
8
4
х 3х х 5
8
8 х
8 1
7
4
3 4 х
3
4 1
8 х 12 х 1
1 0
5. №2
х4
б) у 2
3 х
х
х
2
у
4х х
3
1
2
х 4х
3
1
1
2 1
1 4 2 х
3
2 х
1
1
3
8х
3
2 х
х
6. №3.
в) у х 4 х 2 х 17
5
7 х
7 х
7 1
6
у х 4 х 2 х 1
7
5
4 5 х 2 1 0
5 1
4
20 х 2
7. №4.
х3
г) у
х3 1
2
2
у
1
2
2
х
2
х
2
3 х 1
3
3 х 1
3
1
3 1
2 х 3 3 х 0
2
4
х 9 х
8.
№5.1
1
в) f(x) x , x 2 , x ,
х
3
1
1
1
f (x) x x 1 2
х
х
х
1
1
1
f ( 2 ) 1
2
1 1 ,
2
2
2
1
1
1
3
1
f
1
4.
1
2
1
1
3
1
3
3
9.
№6.3 х
г) f(x)
, x 3, x 0.
2 х
3
х
3 х 2 х 3 х 2 х
f (x)
2
2 х
2 х
5
0 1 2 х 3 х 0 1 2 х 3 х
2
2
2
2 х
2 х
2 х
5
5
f ( 3)
5
2
2
2 ( 3) 1
5
5
1
f 0
1 .
2
2 0 4
4
10.
№7.Найти f (27), если f(x)
f (x)
f
3
х
4
х
4
3
4
х
3
4
1
3
1
3
3
х
4
4
х
3
4
4
4 3
(27) 27 27 3 4
3
3
3
Ответ : f (27) 4
1
3
11.
№8.Найти
1
1
f ( ), если f(x) 4
2
х
1
5
4 1
4
f (x) 4 х 4 х 4 х
х
5
1
5
1
f ( ) 4 4 2 4 32 128
2
2
Ответ : f
1
( ) 128
2
12.
№9.Найти f ( 1), если f (x) 4х
f (x) 4х
4 3 х
3 1
3
2
2х х 5
5
х
2
2х х 5 4х
2 2 х
3
2 1
3
2х
2
1 0 12 х 4 х 1
f ( 1) 12 1 2 4 1 1
12 1 4 1 17
Ответ : f ( 1) 17
2
13.
№10.Найти f (0,5), если f (x) х
f (x) х
3 х
3 1
3
2
9 х х 2
2
х
2
9х х 2 х
9 2 х
3
2 1
3
9х
2
2
1 0 3х 18 х 1
f (0,5) 3 0,5 2 18 0,5 1
3 0,25 9 1 7,25
Ответ : f (0,5) 7,25
14. Спасибо за внимание.
СПАСИБО ЗАВНИМАНИЕ.



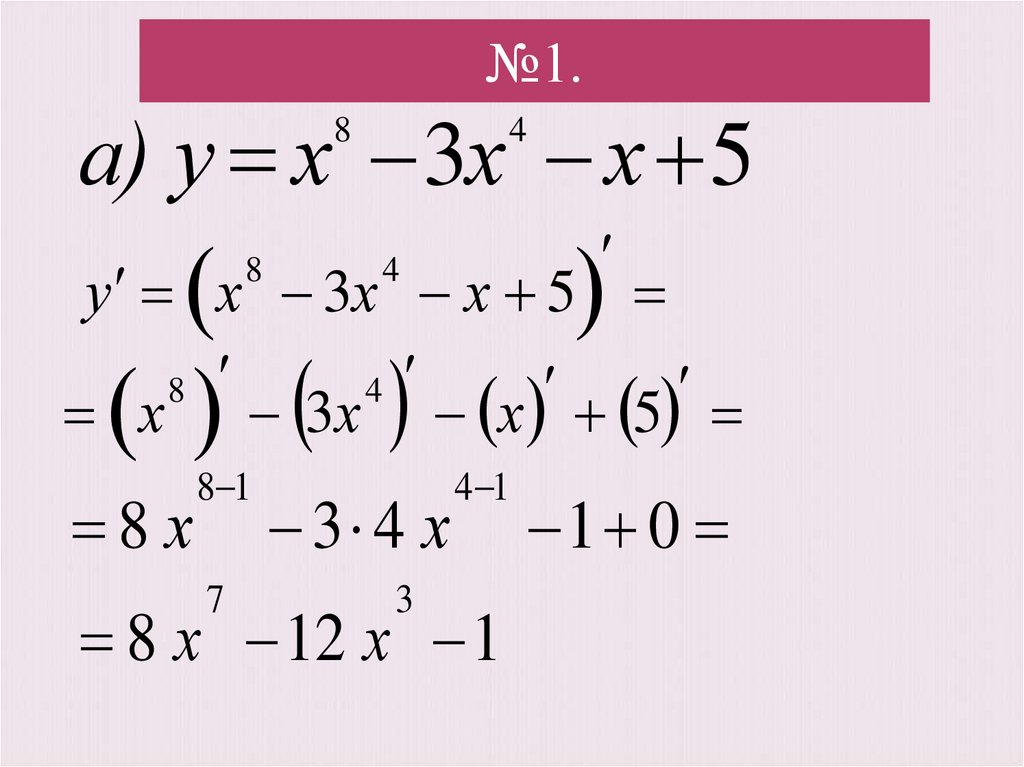
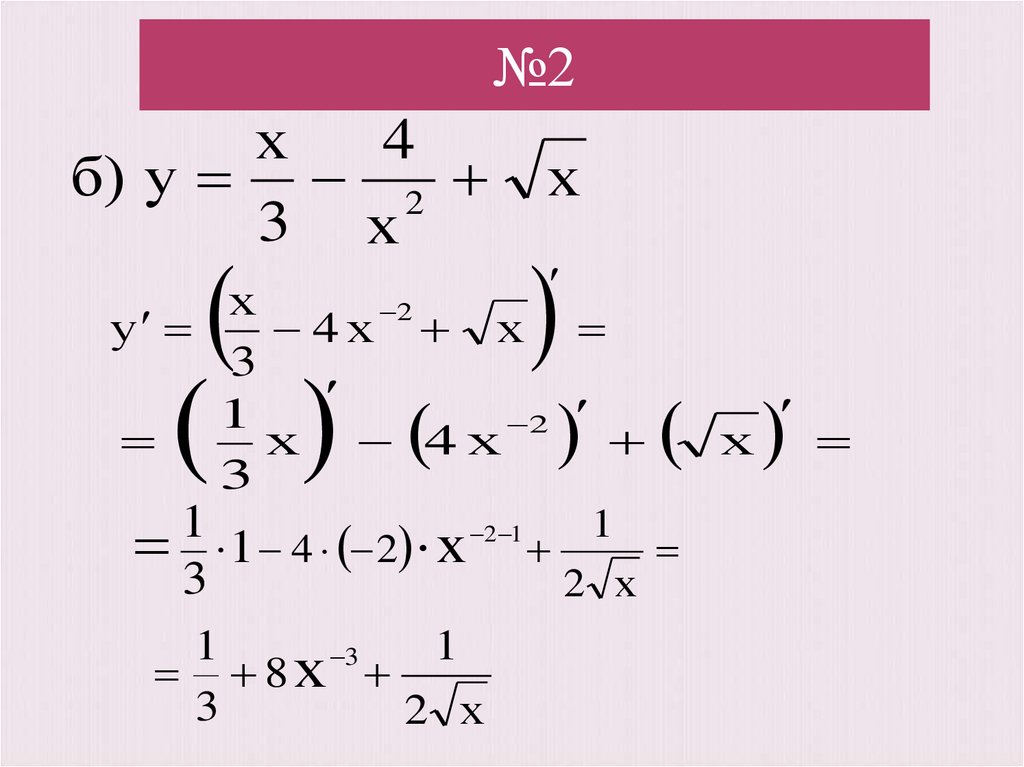
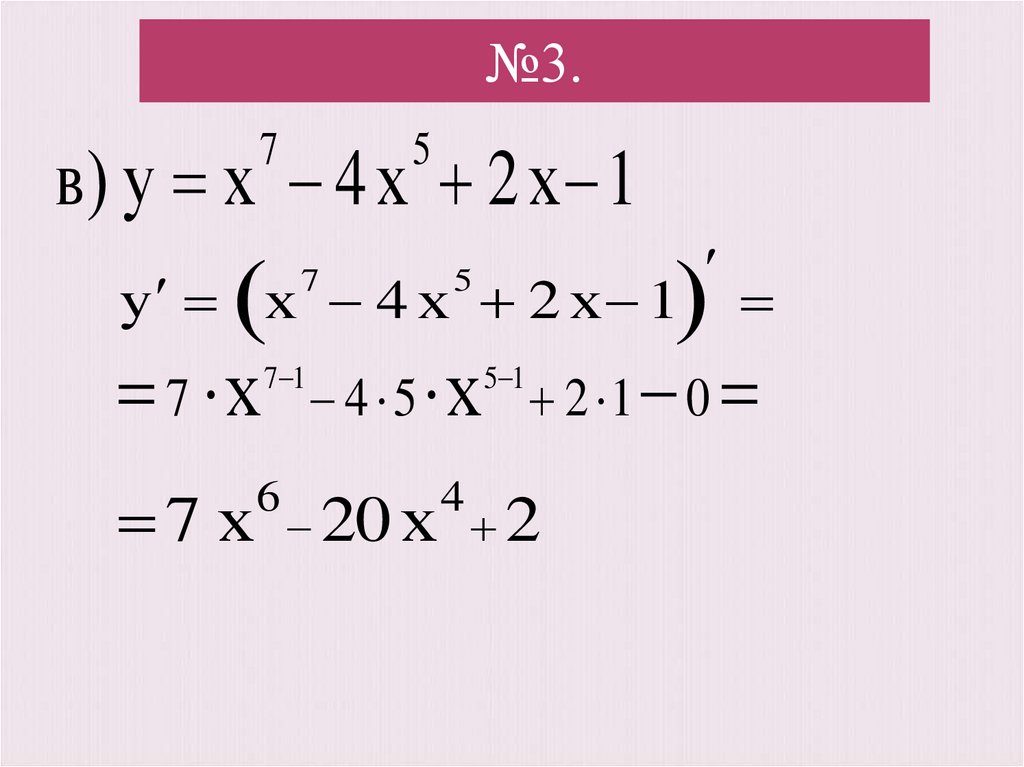

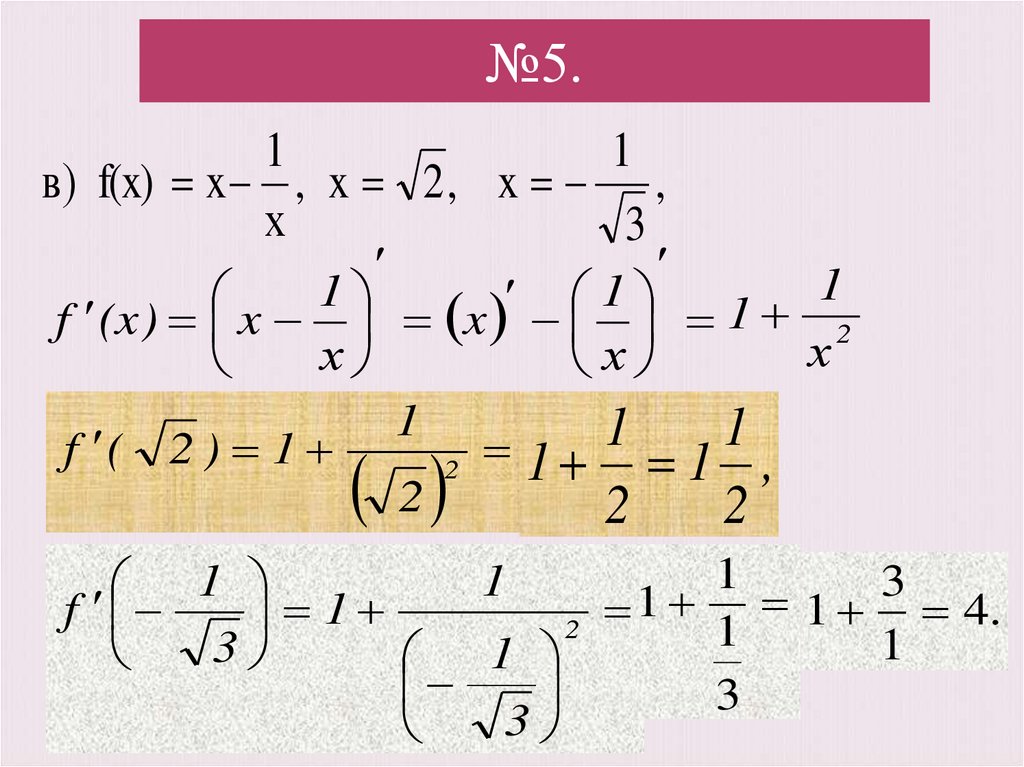






 Математика
Математика








