Компьютерная технология. Управление

1. Компьютерная технология УПРАВЛЕНИЕ

Моделирование
Управление
Наблюдение
Фильтрация
Идентификация
Диагностика
Адаптация
Оптимизация
Визуализация

2.

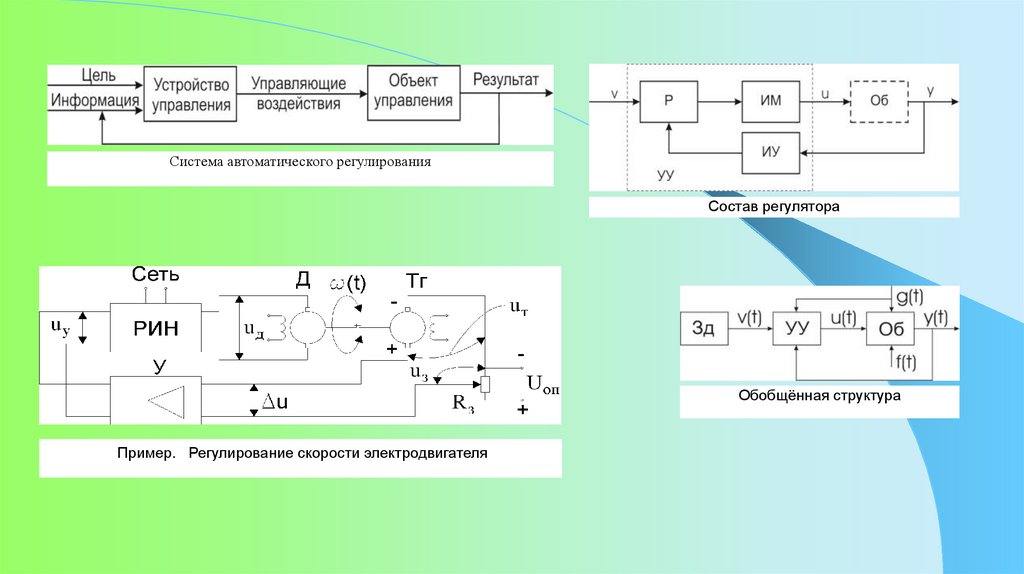
Система автоматического регулирования
Состав регулятора
Обобщённая структура
Пример. Регулирование скорости электродвигателя

3.

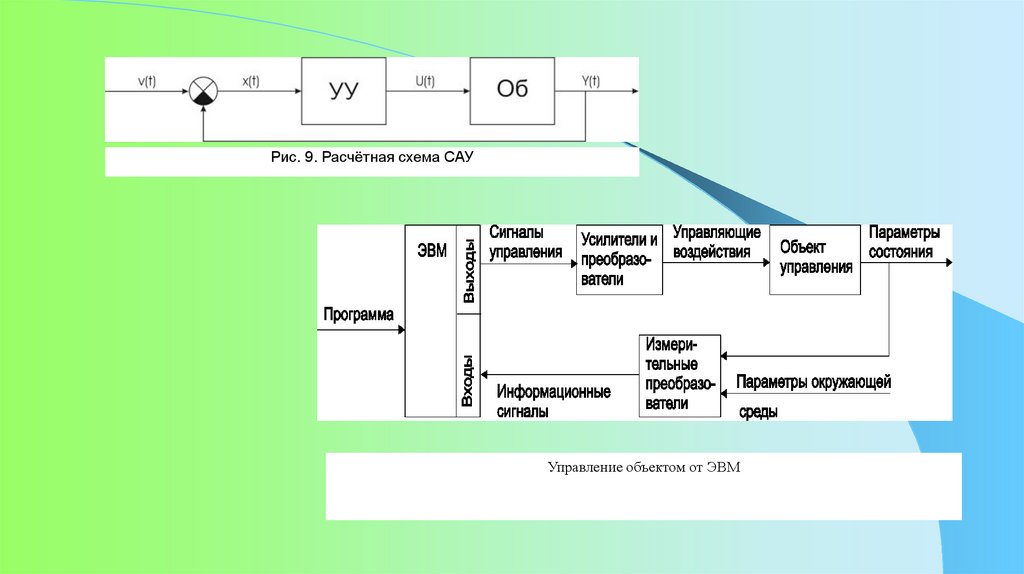
Рис. 9. Расчётная схема САУ
Управление объектом от ЭВМ

4.

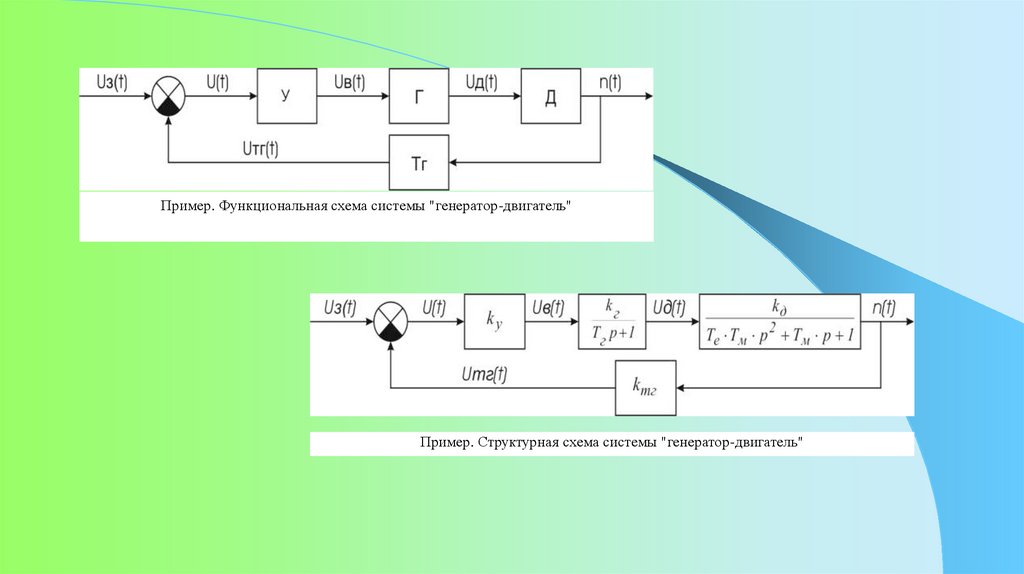
Пример. Функциональная схема системы "генератор-двигатель"
Пример. Структурная схема системы "генератор-двигатель"

5.

y
3
K
1
2
t
0
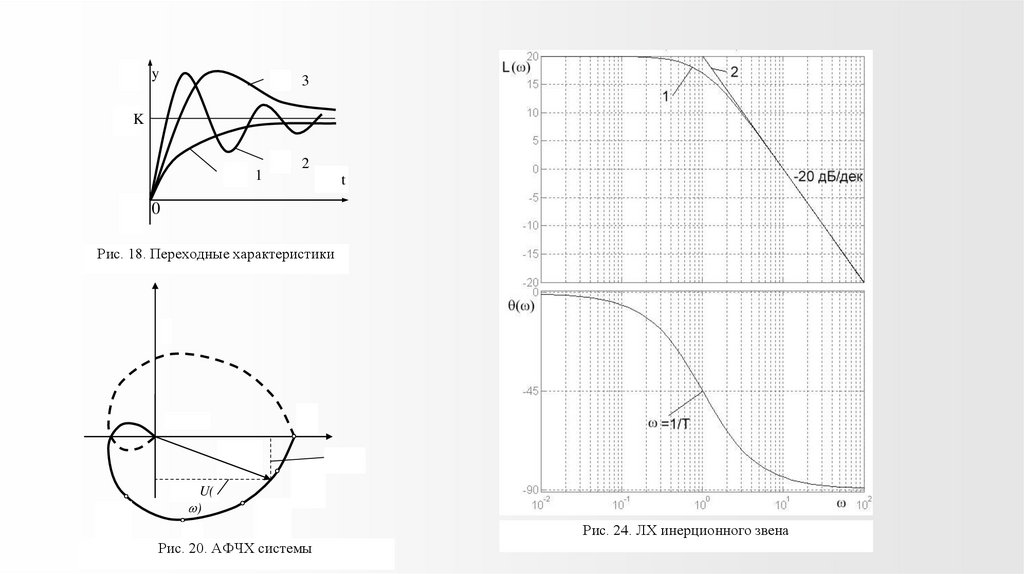
Рис. 18. Переходные характеристики
U(
)
Рис. 24. ЛХ инерционного звена
Рис. 20. АФЧХ системы

6.

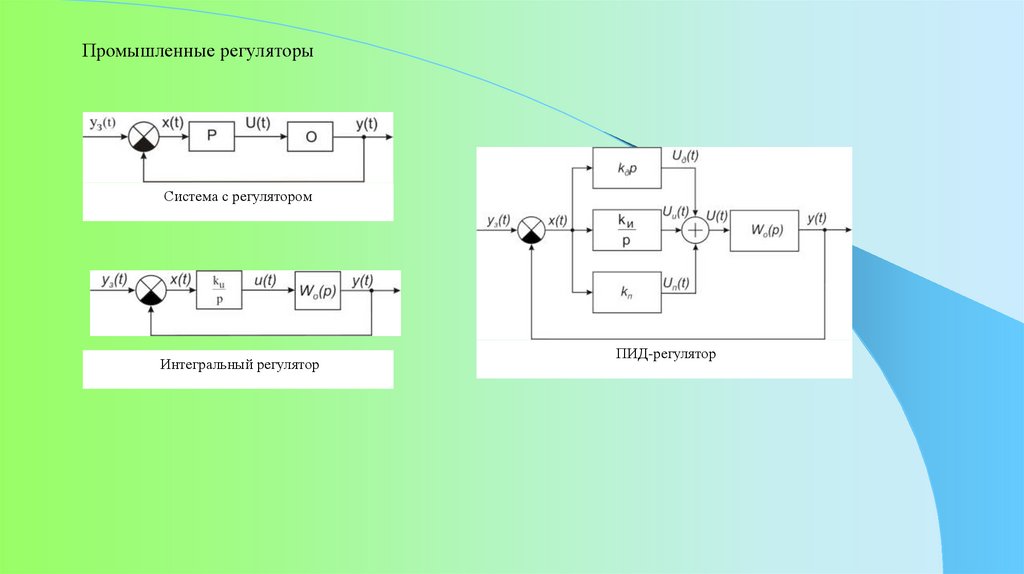
Промышленные регуляторы
Система с регулятором
Интегральный регулятор
ПИД-регулятор

7.

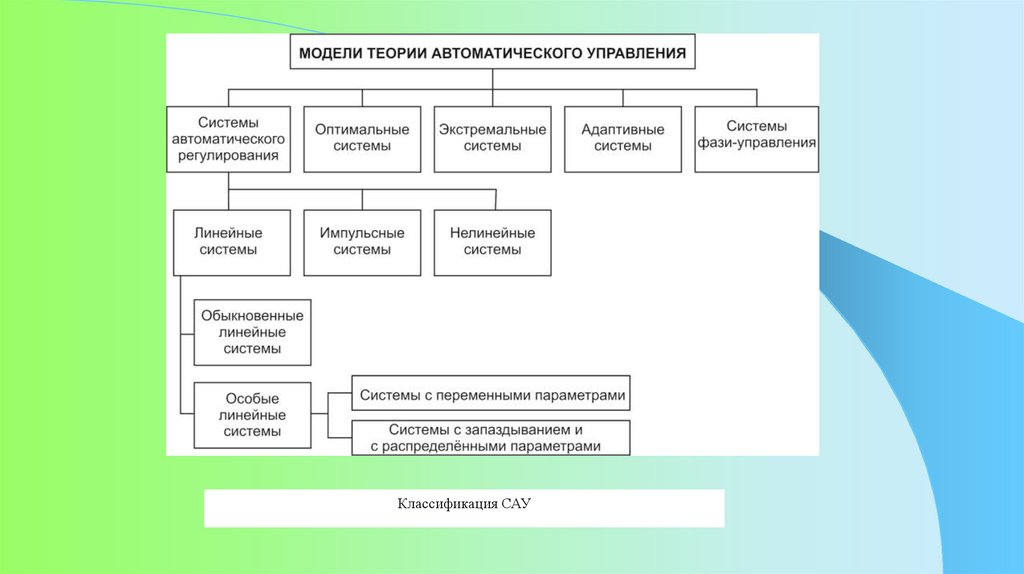
Классификация САУ

8.

Оптимальные системы – в этих системах осуществляется оптимальное управление переводом
объекта из исходного состояния в заданное конечное состояние. Оптимальная модель содержит
дополнительно описание критерия оптимальности, на основе которого оценивается успешность
решения задачи управления.
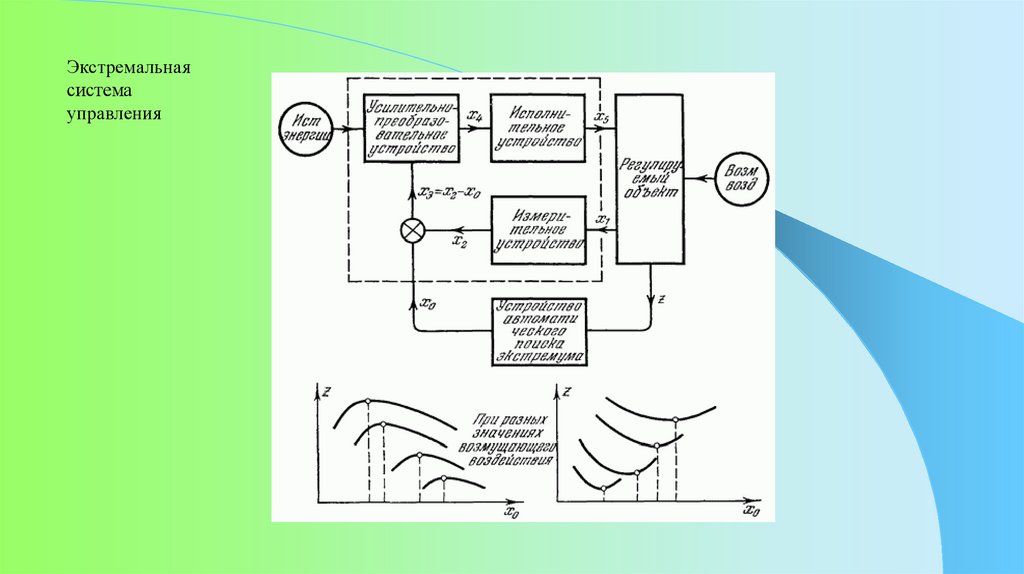
Экстремальные системы – модели, которые позволяют описать и решить задачу экстремального
управления, т.е. автоматического обеспечения экстремума выходной величины объекта
управления в условиях недостаточной априорной информации.
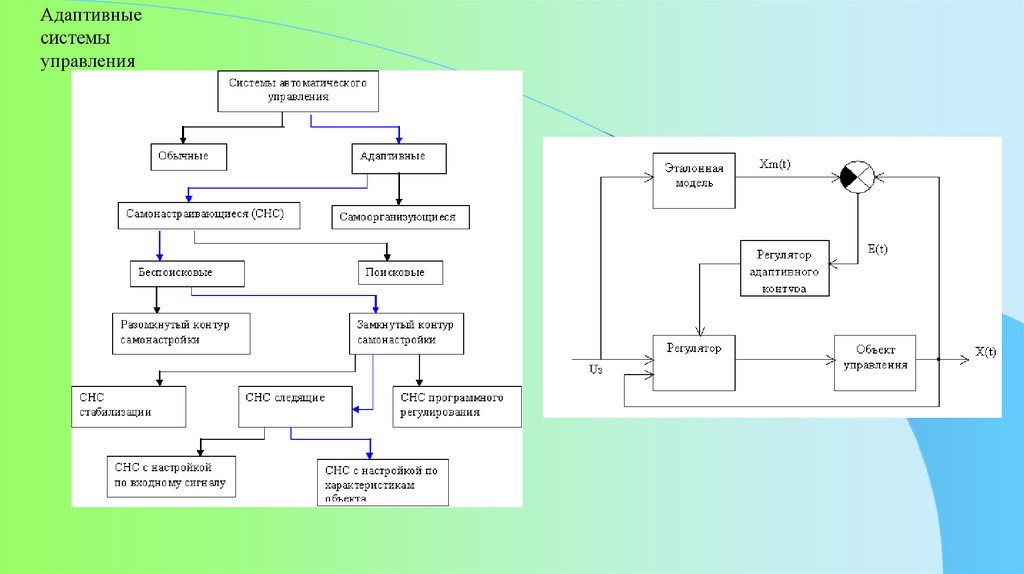
Адаптивные системы – модели, используемые для описания и исследования систем адаптивного
управления, в которых характеристики управления не остаются постоянными, а целенаправленно
изменяются так, чтобы адаптировать поведение системы к конкретным условиям её функционирования.
Системы фази-управления (нечеткое управление, нейро-нечеткое управление) – эти модели позволяют
формализовать качественное (вербальное) описание процесса управления, не поддающегося
детерминированному описанию классическими методами теории управления. Например, с помощью
методов фази-управления можно описать и автоматизировать процесс ручного управления оператором,
осуществляемый на основе личного опыта оператора

9.

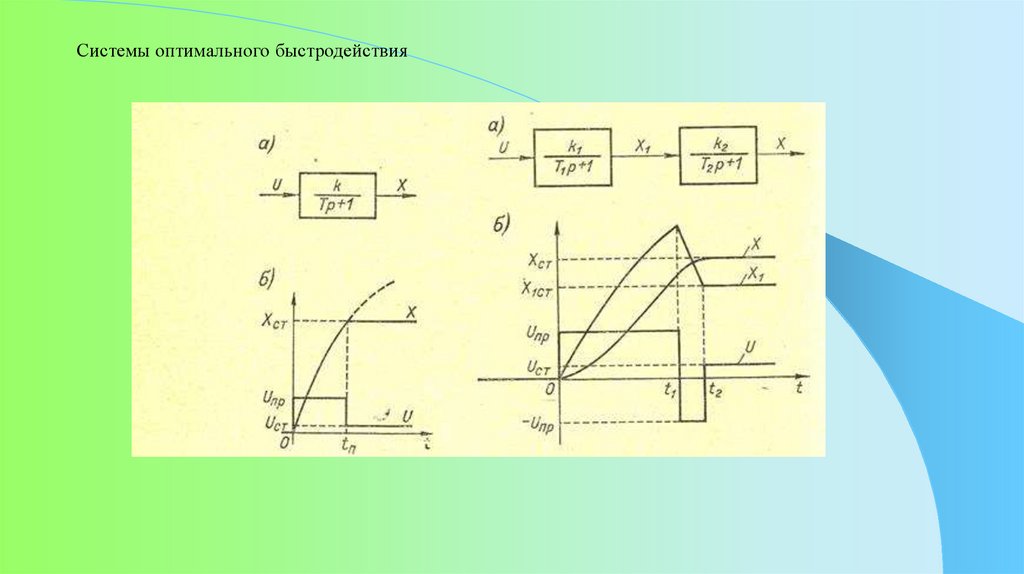
Системы оптимального быстродействия

10.

Экстремальная
система
управления

11.

Адаптивные
системы
управления

12.

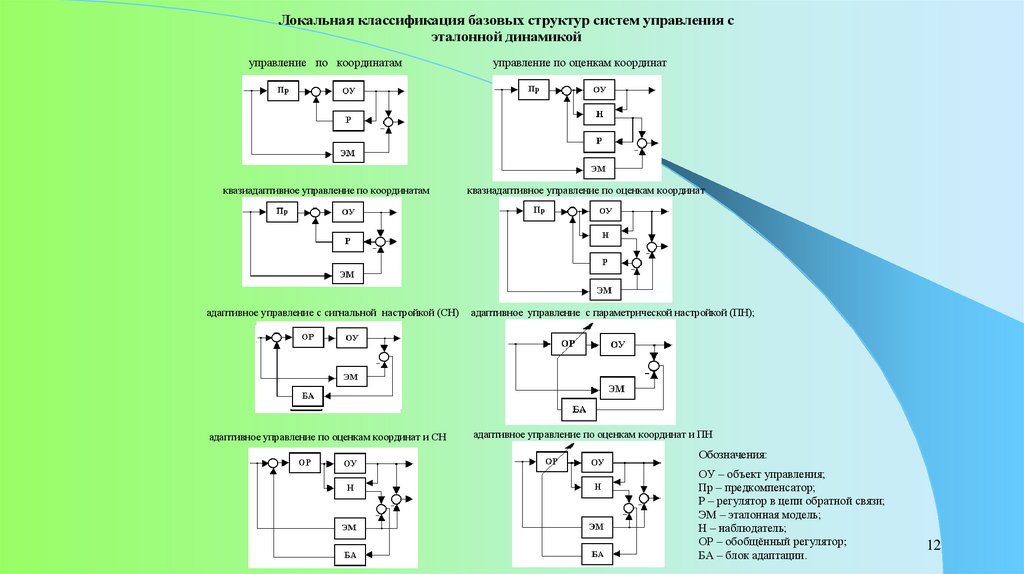
Локальная классификация базовых структур систем управления с
эталонной динамикой
управление по координатам
квазиадаптивное управление по координатам
управление по оценкам координат
квазиадаптивное управление по оценкам координат
адаптивное управление с сигнальной настройкой (СН)
адаптивное управление с параметрической настройкой (ПН);
адаптивное управление по оценкам координат и СН
адаптивное управление по оценкам координат и ПН
Обозначения:
ОУ – объект управления;
Пр – предкомпенсатор;
Р – регулятор в цепи обратной связи;
ЭМ – эталонная модель;
Н – наблюдатель;
ОР – обобщённый регулятор;
БА – блок адаптации.
12

13.

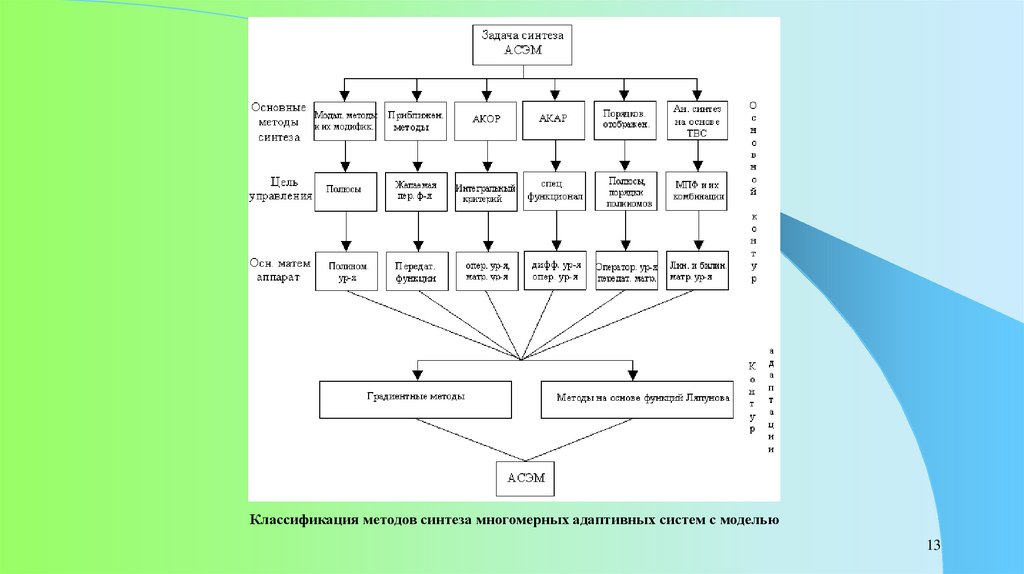
Классификация методов синтеза многомерных адаптивных систем с моделью
13

14.

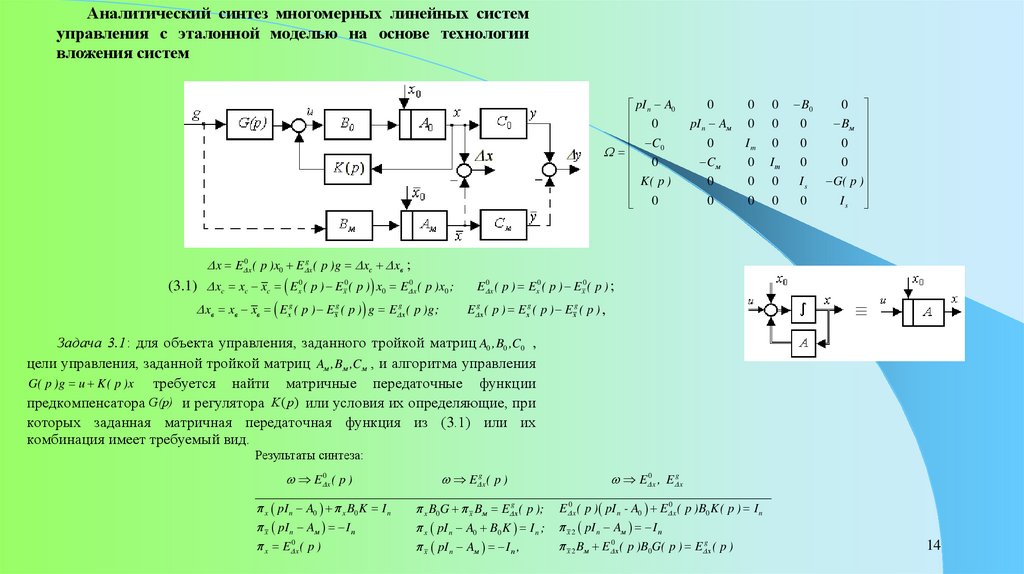
Аналитический синтез многомерных линейных систем
управления с эталонной моделью на основе технологии
вложения систем
pI n A0
0
C0
0
K( p )
0
0
0
0
B0
pI n Aм
0
0
0
0
Im
0
0
C м
0
Im
0
0
0
0
Is
0
0
0
0
Bм
0
0
G( p )
I s
0
x E 0x ( p )x0 E gx ( p )g xс xв ;
(3.1) xc xc xc Ex0 ( p ) Ex0 ( p ) x0 E 0x ( p )x0 ;
xв xв xв Exg ( p ) Exg ( p ) g E gx ( p )g;
E 0 x ( p ) Ex0 ( p ) Ex0 ( p ) ;
E gx ( p ) Exg ( p ) Exg ( p ) ,
Задача 3.1: для объекта управления, заданного тройкой матриц A0 ,B0 ,C0 ,
цели управления, заданной тройкой матриц Aм ,Bм ,Cм , и алгоритма управления
G( p )g u K( p )x
требуется найти матричные передаточные функции
предкомпенсатора G(p) и регулятора K ( p ) или условия их определяющие, при
которых заданная матричная передаточная функция из (3.1) или их
комбинация имеет требуемый вид.
Результаты синтеза:
E 0 x ( p )
x pI n A0 x B0 K I n
x pI n Aм I n
x E 0 x ( p )
E gx ( p )
E 0 x , E gx
x B0G x Bм E gx ( p ); E 0 x ( p ) pI n - A0 E 0 x ( p )B0 K( p ) I n
x pI n A0 B0 K I n ; x 2 pI n Aм I n
x 2 Bм E 0 x ( p )B0G( p ) E gx ( p )
x pI n Aм I n ,
14

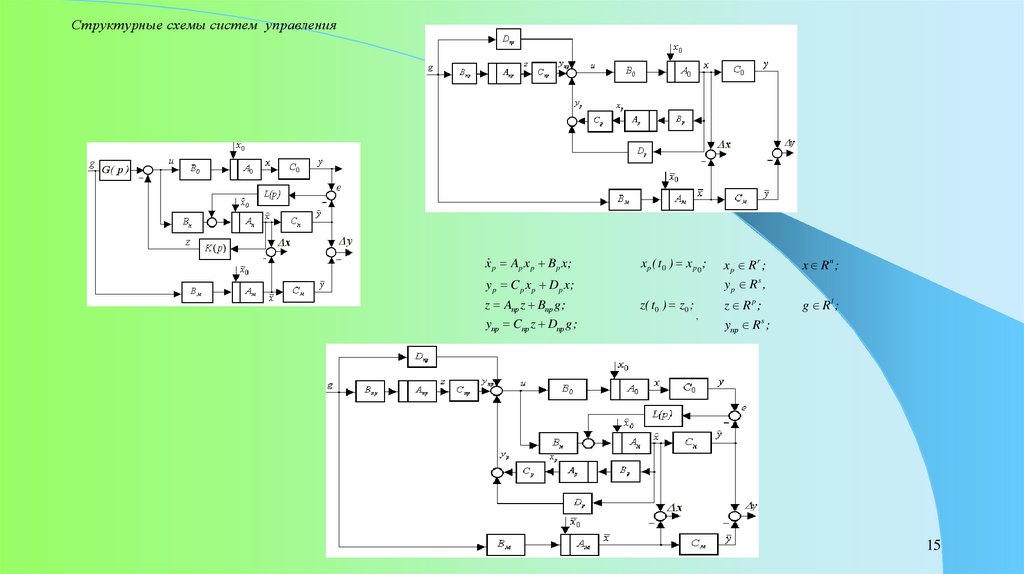
15.

Структурные схемы систем управления
x p Ap x p Bp x;
x p ( t0 ) x p 0 ;
yпp Cпр z Dпр g;
x Rn ;
y p Rs ,
y p C p x p Dp x;
z Aпр z Bпр g;
x p Rr ;
z( t0 ) z0 ;
z Rp;
,
g Rl ;
yпр R s ;
15

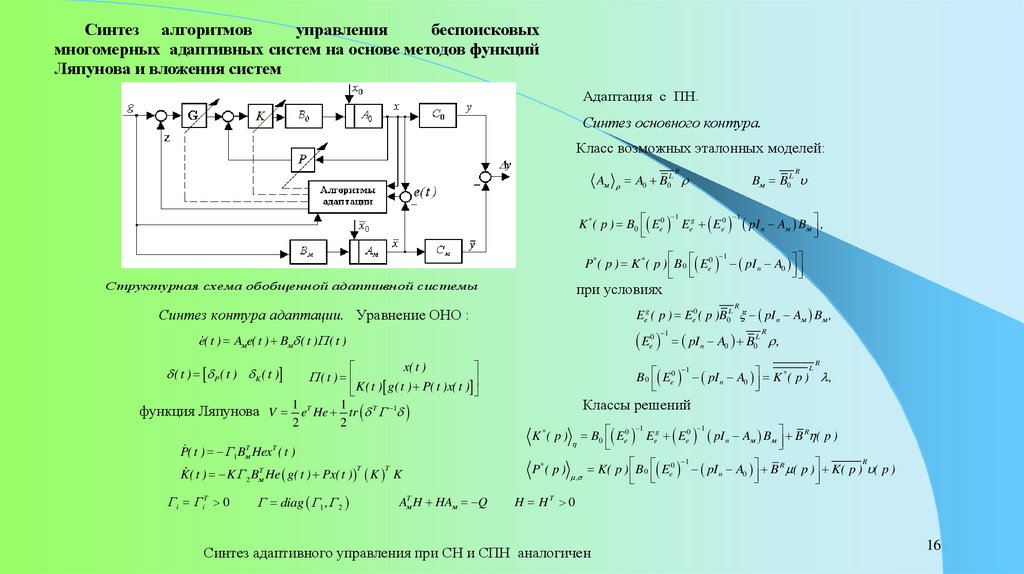
16.

Синтез алгоритмов
управления
беспоисковых
многомерных адаптивных систем на основе методов функций
Ляпунова и вложения систем
Адаптация с ПН.
Синтез основного контура.
Класс возможных эталонных моделей:
R
R
Aм
Bм B0L
A0 B0L
1
1
K * ( p ) B0 Ee0 Eeg Ee0 pI n Aм Bм ,
1
P* ( p ) K * ( p ) B 0 Ee0 pI n A0
Структурная схема обобщенной адаптивной системы
при условиях
Eeg ( p ) Ee0 ( p )B0L pI n Aм Bм ,
R
Синтез контура адаптации. Уравнение ОНО :
E
0 1
e
e( t ) Aмe( t ) Bм ( t ) ( t )
x( t )
(t )
K( t ) g( t ) P( t )x( t )
1
1
функция Ляпунова V eT He tr T 1
2
2
( t ) P ( t ) K ( t )
K( t ) K 2 B He g( t ) Px( t )
T
м
i iT 0
diag 1 , 2
T
K
T
K
AмT H HAм Q
R
R
1
B 0 Ee0 pI n A0 K * ( p ) ,
L
Классы решений
K* ( p )
P( t ) 1BмT HexT ( t )
pI n A0 B0L ,
P* ( p )
1
1
B0 Ee0 Eeg Ee0 pI n Aм Bм B R ( p )
,
1
R
K( p ) B 0 Ee0 pI n A0 B R ( p ) K( p ) ( p )
H HT 0
Синтез адаптивного управления при СН и СПН аналогичен
16

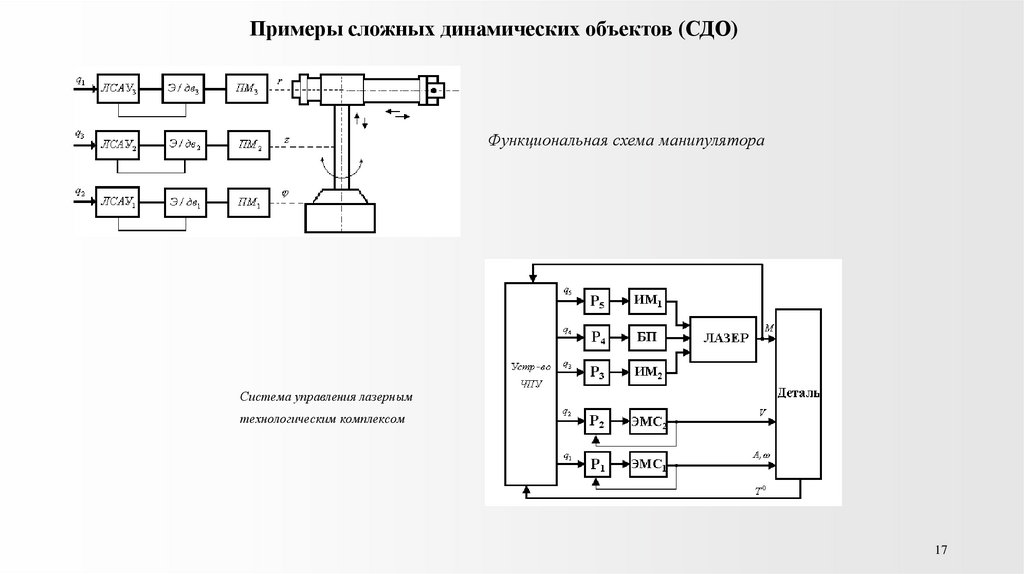
17.

Примеры сложных динамических объектов (СДО)
Функциональная схема манипулятора
Система управления лазерным
технологическим комплексом
17

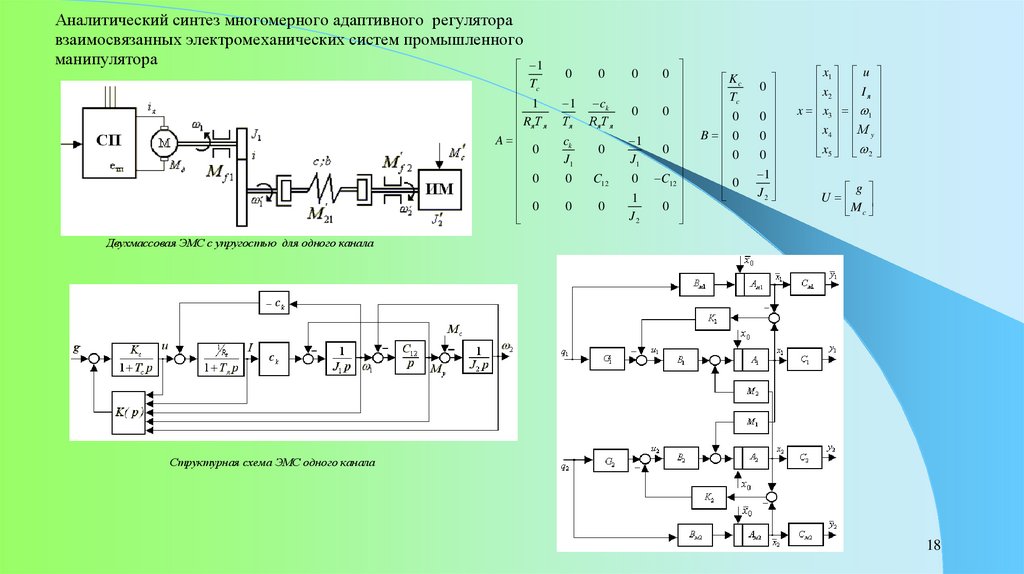
18.

Аналитический синтез многомерного адаптивного регулятора
взаимосвязанных электромеханических систем промышленного
манипулятора
1
T
c
1
R Т
я я
A
0
0
0
0
0
1
Tя
ck
R яТ я
ck
J1
0
0
C12
0
0
0
0
0
1
0
J1
0 C12
1
0
J2
0
Kc
T
c
0
B 0
0
0
0
0
0
0
1
J 2
x1 u
x I
2 я
x x3 1
x4 М y
x5 2
g
U
M c
Двухмассовая ЭМС с упругостью для одного канала
Структурная схема ЭМС одного канала
18

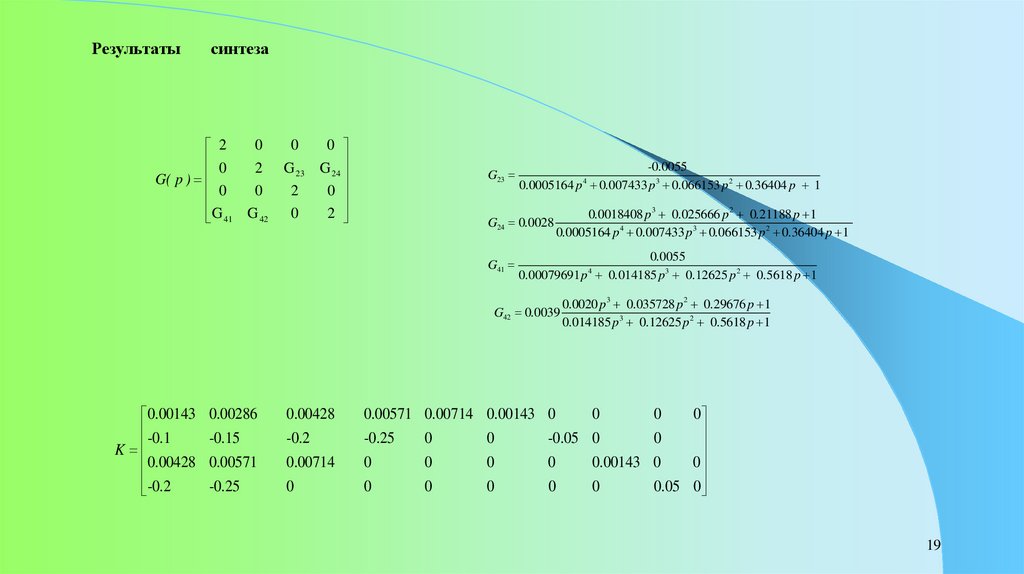
19.

Результаты
синтеза
0
2
0
2
G( p )
0
0
G 41 G 42
0
G 23
2
0
0
G 24
0
2
G23
-0.0055
0.0005164 p 0.007433 p 3 0.066153 p 2 0.36404 p 1
4
G24 0.0028
G41
0.0018408 p3 0.025666 p 2 0.21188 p 1
0.0005164 p 4 0.007433 p3 0.066153 p 2 0.36404 p 1
0.0055
0.00079691 p 0.014185 p3 0.12625 p 2 0.5618 p 1
4
G42 0.0039
0.00143
-0.1
K
0.00428
-0.2
0.0020 p3 0.035728 p 2 0.29676 p 1
0.014185 p3 0.12625 p 2 0.5618 p 1
0
-0.05 0
0
0
0.00143 0
0
0
0
0.05 0
0.00286
0.00428
0.00571 0.00714 0.00143 0
-0.15
-0.2
-0.25
0
0
0.00571
0.00714
0
0
0
-0.25
0
0
0
0
0
0
19