Похожие презентации:
Регуляторы в мехатронных системах управления
1.
Управление промышленнымимехатронными системами
Объем занятий:
18 часов лекций,
54 часов практических занятия,
экзамен.
Храмшин Вадим Рифхатович
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХ
УПРАВЛЕНИЯ
2.
специализированныесоотношения
параметров
автоматической
стабилизации
по виду выполняемых
функций
адаптивные
с переменной
структурой
И, П, ПИ, ПИД
по виду используемой энергии
позиционные
комбинированные
механические
гидравлические
электрические
дискретные
по роду
действия
корректирующие
по назначению
программные
универсальные
непрерывные
прямого
непрямого
по принципу
действия
температуры
давления
уровня
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХ
УПРАВЛЕНИЯ
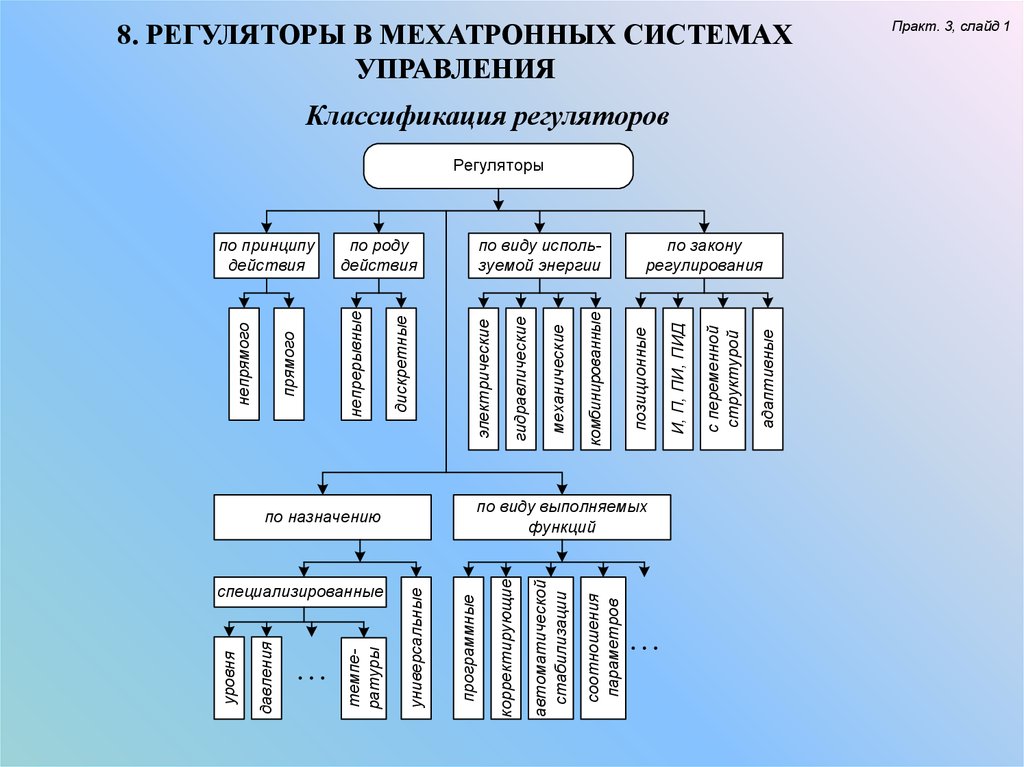
Классификация регуляторов
Регуляторы
по закону
регулирования
Практ. 3, слайд 1
3.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 2
Выбор типа регулятора
Для выбора типа регулятора и определения его настройки необходимо знать:
- статические и динамические характеристики объекта регулирования;
- требования к качеству процесса регулирования;
- характер возмущающих воздействий, действующих на объект регулирования.
Минимальное время регулирования
Закон регулирования
Трег /
.
П
6,5
ПИ
12
ПИД
7
ПИ регулятор, обладает следующими достоинствами:
- обеспечивает нулевую статическую ошибку регулирования;
- сравнительно прост в настройке, так как настраиваются только два параметра –
коэффициент усиления k и постоянная интегрирования ТИ;
- в регуляторе имеется возможность оптимизации k/ТИ→max, что обеспечивает
управление
с
минимально
возможной
среднеквадратичной
ошибкой
регулирования;
- малая чувствительность к шумам в канале измерения (в отличие от ПИД
регулятора).
4.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Типовой процесс регулирования
Тип
минимум
апериос 20 %
регулятора
интегрального
дический
перерегулированием
критерия качества*
Статический объект регулирования
0 ,3 Т
0 ,7 Т
0 ,9 Т
КП
КП
КП
П
k
k
k
0 ,6 Т
0 ,7 Т
Т
,
,
,
КП
КП
КП
ПИ
k
k
k
Т И 0 ,6 Т
Т И 0 ,7 Т
ТИ Т
0 ,95 Т
,
k
. Т И 2 ,4 ,
Т Д 4 ,4
КП
ПИД
П
ПИ
1,4 Т
,
k
1,3 ,
0 ,5
КП
ТИ
ТД
Астатический объект регулирования
0 ,4 Т
0 ,7 Т
КП
КП
КП
0 ,4 Т
0 ,6 Т
ТИ 5 ,
Т Д 0 ,2
-
,
ТИ 6 Т
КП
ПИД
1,2 Т
,
k
ТИ 2 ,
Т Д 0 ,4
КП
КП
0 ,7 Т
,
ТИ 3 Т
,
КП
1,1 Т
ТИ 2 ,
Т Д 0 ,4
КП
Т
,
ТИ 4 Т
,
КП
1,4 Т
,
Т И 1,6 ,
Т Д 0 ,5
Практ. 3, слайд 3
Определение
параметров
регуляторов для
различных типовых
процессов
регулирования
5.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 4
h t
4
3
1
2
.
t
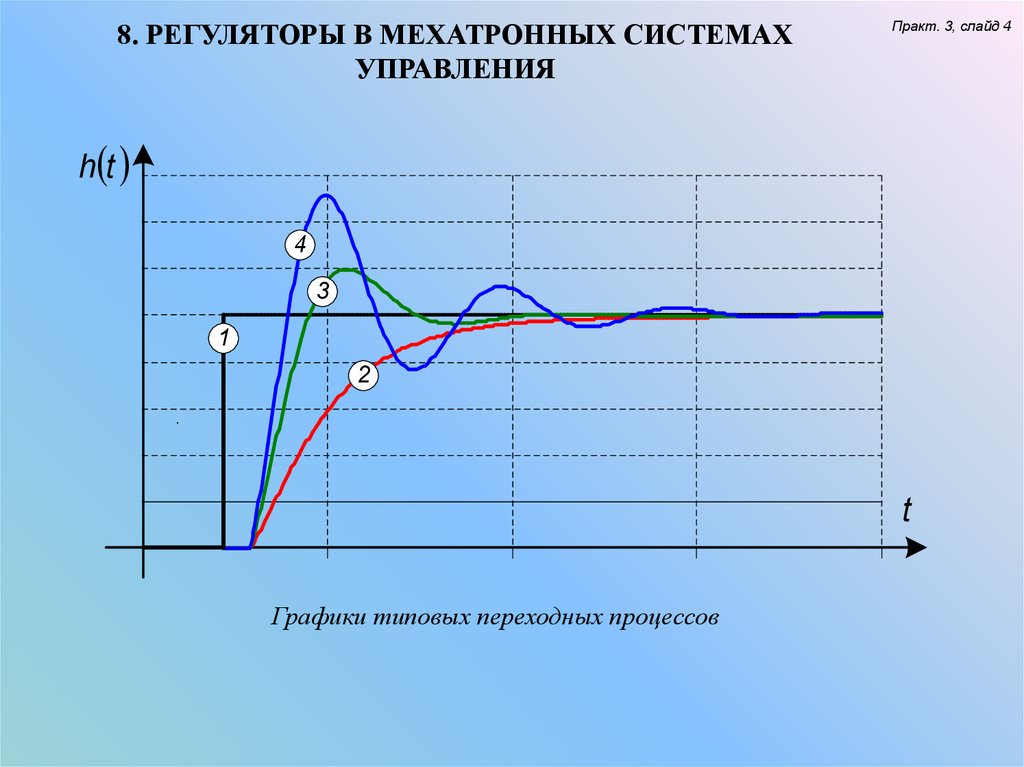
Графики типовых переходных процессов
6.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 5
Идентификация элементов мехатронных систем
Статические характеристики объекта управления
Y
Y
Y
y
y
x
.
Х max
Х min
а
Y1
x
Х
Yэкстрем
Х
Х max
Х min
б
Х1 1 Х1 2 Х
Х min Х опт Х max
в
Вид статических характеристик объектов управления
y
k const
х
Y Y0 k х
y
k f Х
х
7.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 6
Линеаризация нелинейной зависимости Y = f(Х) в ряд Тейлора для точки исходного
состояния Х0
2
n
f X 0
2 f X 0
n f X 0
Y f Х 0 х
х
х
1
2
n
f X 0
Для большинства промышленных объектов Y f Х 0 х
1
Поскольку f Х 0 Y0 f X 0
то
f X 0 k x
dy
dx
Y Y0 k х
Экстремальные статические характеристики можно отнести к существенно
нелинейным характеристикам, коэффициент передачи которых меняет свой знак
при изменении входного параметра в допустимых пределах.
Y1 f Х1 1 f Х1 2
8.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 7
Линия регрессии Y / Х a b Х с Х 2 q Х n
Близость каждой экспериментальной точки к линии регрессии Y / (X) измеряется
отрезком ординаты
Yi Y i Y / Х i
Расчет коэффициентов линии регрессии методом наименьших квадратов основан
на соблюдении условия
Y Y
n
i
i 1
/
Х i
2
min
Для линии регрессии линейной зависимости Y / (X) = a + b · X это выражение
приводится к виду
n
S a, b Y i Y
i 1
/
Х i
2
n
Y i a b X i 2 min
i 1
Величины коэффициентов a и b уравнения, удовлетворяющие условиям
минимума функции S(a,b) могут быть определены из уравнений
dS a, b
0
da
dS a, b
0
db
9.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 8
n
S a, b Yi2 2 a Y i 2 b Y i X i a2 2 a b X i b2 X i2
i 1
n
n
dS a, b n
2 Yi 2 a 2 b X i 0
da
i 1
i 1
i 1
n
n
dS a, b n
2 Yi X i 2 a X i 2 b X i2 0
db
i 1
i 1
i 1
Тогда для нахождения значений коэффициентов a и b регрессии
линейной зависимости можно записать систему уравнений
i 1
i 1
n
n
n
Yi X i a X i b X i2
i 1
i 1
i 1
n
n
Yi n a b X i
10.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Пример 1.
Для
изготовления
пластиковых
емкостей
на
автоматическом формующем
прессе существует обратная
пропорциональная
зависимость между давлением
сжатого воздуха в магистрали и
толщиной стенки формуемого
изделия. При построении АСУ
ТП такого пресса возникают
вопросы:
- какая будет толщина
стенок формуемого изделия
при
постоянном
давлении
воздуха;
- каким должно быть
давление воздуха для привода
формующего пресса, чтобы
получить заданную толщину
стенки?
Практ. 3, слайд 9
№
Давление, Pi
Толщина, hi
Pi hi
Pi2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
8,0
8,5
9,0
9,5
10,0
8,0
8,5
9,0
9,5
10,0
8,0
8,5
9,0
9,5
10,0
8,0
8,5
9,0
9,5
10,0
4,62
4,12
3,21
2,86
1,83
4,5
3,88
3,05
2,53
2,02
4,43
4,01
3,16
2,71
2,24
4,81
3,67
3,30
2,62
1,95
36,96
35,02
28,29
27,17
18,30
36,00
32,98
27,45
24,04
20,20
35,44
34,09
28,44
25,74
22,40
38,48
31,20
31,50
24,89
19,50
64,00
72,25
81,00
90,25
100,0
64,0
72,25
81,00
90,25
100,0
64,0
72,25
81,0
90,25
100,0
64,00
72,25
81,00
90,25
100,0
180
65,52
576,88
1630
11.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 10
Учитывая, что Pi Х i , hi Yi и подставив их значения из табл. в
систему для определения коэффициентов а и b получим
65 ,52 20 a 180 b
.
576 ,88 180 a 1630 b
Откуда b = -1,28, a = 14,796.
В итоге искомая зависимость будет иметь вид
h 14,796 1,28 P .
Для линии регрессии
S a, b,c
Y / (X) = a + b · X + c · X2
n
2 2
Y i a b X i c X i
i 1
min
По аналогии с предыдущим случаем коэффициенты a, b и c могут быть
определены из уравнений
dS a, b,c
dS a, b,c
dS a, b,c
0,
0,
0
da
db
dc
12.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
n
S a, b,с Yi2 2 a Y i 2 b Y i X i 2 с Y i X i2 a2 2 a b X i
i 1
2 a с X i2 b2 X i2 2 b c X i3 c 2 X i4
n
n
n
dS a, b,c n
2 Yi 2 a 2 b X i 2 c X i2 0 ;
da
i 1
i 1
i 1
i 1
n
n
n
dS a, b,c n
2
2 Yi X i 2 a X i 2 b X i 2 c X i3 0 ;
db
i 1
i 1
i 1
i 1
n
n
n
dS a, b,c n
2
2
3
2 Yi X i 2 a X i 2 b X i 2 c X i4 0 ,
dс
i 1
i 1
i 1
i 1
n
i 1
i 1
n
n
n
2
3
Xi a Xi b Xi c Xi
i 1
i 1
i 1
n
n
n
2
2
3
4
Xi a Xi b Xi c Xi
i 1
i 1
i 1
n
n
Yi n a b X i c X i2
i 1
n
Yi
i 1
n
Yi
i 1
Практ. 3, слайд 11
13.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 12
Совместный анализ выражений, используемых для расчета
коэффициентов линий регрессии 1-го и 2-го порядка, позволяет выявить
аналогию и составить системы и для уравнений более высоких
порядков. Так для уравнения Y / (X) = a + b · X + c · X2 + d · X3
коэффициенты могут быть определены из системы
n
Yi
i 1
n
Yi
i 1
n
Yi
i 1
n
Yi
i 1
n
2
3
n a b Xi c Xi d Xi
i 1
i 1
i 1
n
n
n
n
2
3
4
Xi a Xi b Xi c Xi d Xi
i 1
i 1
i 1
i 1
n
n
n
n
X i2 a X i2 b X i3 c X i4 d X i5
i 1
i 1
i 1
i 1
n
n
n
n
X i3 a X i3 b X i4 c X i5 d X i6
i 1
i 1
i 1
i 1
n
n
14.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 13
Пример 2. Рассчитать уравнение регрессии статической
характеристики технологического агрегата с постоянным притоком тепла
и регулированием температуры рабочего пространства путем вдувания
атмосферного воздуха.
Экспериментально были получены следующие значения температур
рабочего пространства при различной степени открытия поворотного
клапана, регулирующего подачу охлаждающего воздуха температурой
20ºС в рабочее пространство.
15.
Практ. 3, слайд 148. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХ
УПРАВЛЕНИЯ
№
1
Угол
Темпеповорота
ратура,
вала Х i ,
Yi , ºС
%
0
700
Х i2
Х i3
Х i4
Х i Yi
Х i2 Yi
2
10
580
100
1000
100000
5800
58000
3
20
510
400
8000
16000
10200
204000
4
30
460
900
27000
810000
13800
414000
5
40
410
1600
64000
250000
16400
656000
6
50
370
2500
125000
6250000
18500
925000
7
60
330
3600
216000
12960000
19800
1188000
8
70
300
4900
343000
24010000
21000
1450000
9
80
290
6400
512000
40960000
23200
1856000
10
90
280
8100
729000
65610000
25200
2268000
11
100
450
ход механизма ограничен диапазоном 0…90%
4230
28500 2025000
153330000
153900
9039000
16.
Практ. 3, слайд 158. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХ
УПРАВЛЕНИЯ
Получим систему уравнений
4230 10 a 450 b 28500 c
153900 450 a 28500 b 2025000 c
,
9039000 28500 a 2025000 b 153330000 c
решение которой дает значения коэффициентов
a = 681,5, b = -8,92, с = 0,05.
Тогда искомое уравнение будет
Y Х 681,5 8 ,92 Х 0 ,05 Х 2 .
Статическая
характеристика объекта
управления
Y , 0С
650
550
450
350
250
0
20
40
60
80
Х, %
17.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Динамические характеристики объекта управления
an
bm
dmX
dt m
d nY
dt n
bm 1
a
n
an 1
d m 1 X
dt m 1
d n 1Y
dt n 1
a1
b1
dY
a0
dt
dX
b0 ,
dt
pn an 1 pn 1 a1 p a0 Y
bm pm bm 1 pm 1 b1 p b0 X
Тогда передаточная функция объекта управления принимает вид
an p n an 1 p n 1 a1 p a0
Y
Wоб p
X bm p m bm 1 p m 1 b1 p b0
Практ. 3, слайд 16
18.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 17
Различают следующие динамические характеристики:
- кривая разгона (переходная функция), представляющая собой реакцию
объекта на однократное скачкообразное управляющее воздействие;
- импульсная характеристика, являющаяся реакцией объекта на
воздействие в форме импульса;
- частотные характеристики, представляющие собой реакцию объекта на
гармонический входной сигнал постоянной амплитуды и различной частоты.
По виду кривой разгона все реальные объекты управления можно разделить
на три вида: статические (с самовыравниванием), астатические (без
самовыравнивания) и с запаздыванием.
19.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
газ
Х
воздух
дым
x
Х нач
t
Y
Qвх Х
y
Yнач
Qвых Y
t
а
Х
Qвх Х
x
Х нач
Y
t
Y
y
Qвых const
Yнач
t
б
Х
L
Qвх Х
x
Х нач
V
t
Y
L
V
Y
Qвых
в
Yнач
y
t
Практ. 3, слайд 18
Примеры объектов управления
различного вида
и соответствующие им
траектории кривых разгона:
а – статический объект с
самовыравниванием;
б – астатический объект без
самовыравнивания;
в – статический объект с
запаздыванием и с
самовыравниванием
20.
Практ. 3, слайд 198. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХ
УПРАВЛЕНИЯ
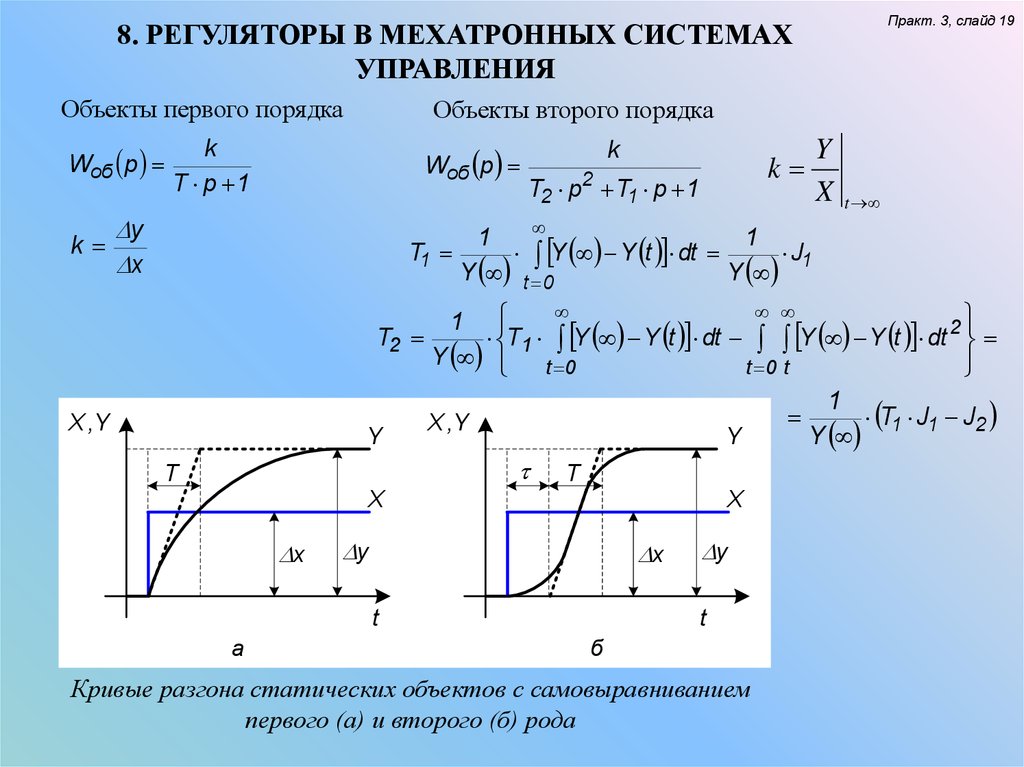
Объекты первого порядка
Wоб p
k
Объекты второго порядка
k
T p 1
Wоб p
y
х
k
Y
X
k
T2 p2 T1 p 1
t
1
1
T1
Y Y t dt
J1
Y t 0
Y
1
T2
Т1 Y Y t dt Y Y t dt 2
Y t 0
t 0 t
Х ,Y
Y
Х ,Y
Y
Т
Т
Х
х
Х
y
х
t
а
y
t
б
Кривые разгона статических объектов с самовыравниванием
первого (а) и второго (б) рода
1
T1 J1 J2
Y
21.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 20
Пример 3. Необходимо определить коэффициенты передаточной функции
объекта управления по экспериментальной переходной характеристики
температуры поверхности металла во второй сварочной зоне четырехзонной
методической печи, заданной таблично. Температура поверхности (точнее слоя
окалины) измерялась пирометром полного излучения, способным фиксировать
всплески тепловой радиации факела. Заданы = 4 с, Т = 19 с и k = 0,87 ºС/%
Время,
с
1
4
11,5
20
30
40
50
60
80
Интервал
времени
разбиения Δt, с
2
7,5
9,5
10
10
10
10
20
-
{[Y(∞)-Y(ti)] +
Выходная
Y(∞)-Y(t)
величина Y
+ [Y(∞)-Y(ti+1)]} / 2 * Δti
3
0,00
0,46
0,65
0,76
0,84
0,87
0,88
0,89
4
0,89
0,43
0,24
0,13
0,05
0,02
0,01
0
5
4,95
3,18
1,85
0,9
0,35
0,15
0,1
0
22.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Время,
с
1
4
11,5
20
30
40
50
60
80
J1=Σ5i, i=k…m
[J1(i) + J1(i+1)] / 2 * Δti
J2=Σ7i, i=k…m
6
11,78
6,83
3,65
1,8
0,6
0,25
0,1
0
7
69,79
49,78
27,25
12,00
4,25
1,75
1,0
0
8
165,84
96,05
48,25
19,
7
2,75
1,0
0
Таким образом, значения коэффициентов передаточной функции
определяется:
Y 0 ,89
0 ,89 ,
X
1
1
1
Т1
J1
11,78 13 ,23 ,
Y
0 ,89
1
1
Т2
T1 J1 J2
11,78 13 ,23 165 ,84 11,14 ,
Y
0 ,89
k
а передаточная функция будет иметь вид
Wоб p
0 ,89
2
11,14 p 13 ,23 p 1
.
Практ. 3, слайд 21
23.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 22
Экспериментальные методы настройки регуляторов
Метод незатухающих колебаний (выведение системы на границу колебательной
устойчивости )
- для П регулятора
К 0 ,55 К кр ;
- для ПИ регулятора
К 0 ,45 К кр , Т И
Т кр
1,2
;
- для ПИД регулятора
К 0 ,6 К кр , Т И
Т кр
2
, ТД
Т кр
8
.
Метод затухающих колебаний (с декрементом затухания ε= ¼ )
- для ПИ регулятора
Т
ТИ к ;
6
- для ПИД регулятора
Т
Т
ТИ к , Т Д к ;
1,5
6
24.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Пример настройки ПИД регулятора температуры
Т
Практ. 3, слайд 23
Т
Т уст
4
1
Т уст
2
3
2
1
3
4
5
Т нач
а
Т
t Т нач
в
Т уст
1
2
Т нач
б
t
t
Настройка ПИД регулятора температуры:
а - переходная характеристика при
настройке зоны пропорциональности;
б - при настройке дифференциальной
компоненты;
в - при настройке интегральной
компоненты
25.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Практ. 3, слайд 24
Функциональная схема (а) паронагревателя с ПИД регулятором и структурная
схема контура регулирования угла поворота шарового сегмента клапана (б)
SP
ПИД
подача
пара
паронагреватель
холодная
жидкость
нагретая
жидкость
Т
конденсат
а
з
WПИД
k o
U зЭП
t
б
WЭП
WПН
φз – уставка положения клапана,
формируемая в зависимости от требуемой
температуры жидкости в соответствии со
статической характеристикой
паронагревателя WПН;
WПИД – передаточная функция ПИД
регулятора;
WЭП – передаточная функция
электропривода поворотного клапана;
UзЭП – сигнал задания на электропривод
(управляющее воздействие регулятора);
kоφ – коэффициент обратной связи по углу
поворота;
φ – угол поворота клапана;
t – температура нагреваемой жидкости.
W p
WПИД p WЭП p
1 WПИД p WЭП p WПН p kо
26.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
Функциональная схема паронагревателя с ПИД регулятором и
упреждающей коррекцией
SP
ПИД
подача
пара
F
паронагреватель
холодная
жидкость
Т
нагретая
жидкость
конденсат
UзЭП з kо WПН p WПИД p F p
Практ. 3, слайд 25
27.
8. РЕГУЛЯТОРЫ В МЕХАТРОННЫХ СИСТЕМАХУПРАВЛЕНИЯ
SP
ПИД1
W p
ПИД2
Практ. 3, слайд 26
WПИД1 WПИД2 WЭП WПН
1 WПИД2 WЭП kо WПИД1 WПИД2 WЭП WПН kоt
подача
пара
F
паронагреватель
холодная
жидкость
Т
нагретая
жидкость
конденсат
а
tз
WПИД1
з
WПИД 2
U зЭП
k o
k ot
б
WЭП
WПН
t
Функциональная схема (а)
каскадного управления
паронагревателем и
структурная ее схема (б)
























 Программное обеспечение
Программное обеспечение Механика
Механика








