Бегущие волны. Вторичные параметры

1.

1
Лекция 2
Бегущие волны.
Вторичные параметры
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

2.

2
В общем случае решение дифференциальных
уравнений
i
u
x r0i L0 t ;
i
u
g 0u C0
x
t
представляет комбинацию так называемых
бегущих волн, являющихся функциями
времени t и координаты x.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

3.

Синусоидальный режим линии также
характеризуется наличием бегущих волн,
структуру которых легко установить на основе
соотношений (5):
3
1
1
x
x
U
(
x
)
(
U
I
Z
)
e
(
U
I
Z
)
e
;
1
1
в
1
1
в
2
2
1
1
x
x
I ( x)
(U1 I1Z в )e
(U1 I1Z в )e .
2Zв
2Zв
Воспользуемся первым уравнением системы и
перейдем от комплексного значения напряжения
к мгновенному.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

4.

Поскольку выражения в скобках представляют
собой комплексные числа, не зависящие от х,
то вводим обозначения:
4
1
j п
(U1 I1Z в ) U п1 U п1e ;
2
1
j о
(U1 I1Z в ) U о1 U о1e
2
и представим комплексы составляющих правой
части в форме:
U п ( x) U п1e
x
прямая волна
;
x
U о ( x) U о1e .
обратная волна
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

5.

Учитывая, что
j , можно записать:
5
U ( x) U п ( x) U о ( x)
e
x
U п1e
j ( п x )
x
e U о1e
j ( о x )
и перейти к мгновенным значениям:
u ( x , t ) uп ( x , t ) u o ( x , t )
e xU пm sin( t п x)
e xU оm sin( t о x),
где U пm
2U п1; U оm 2U о1.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

6.

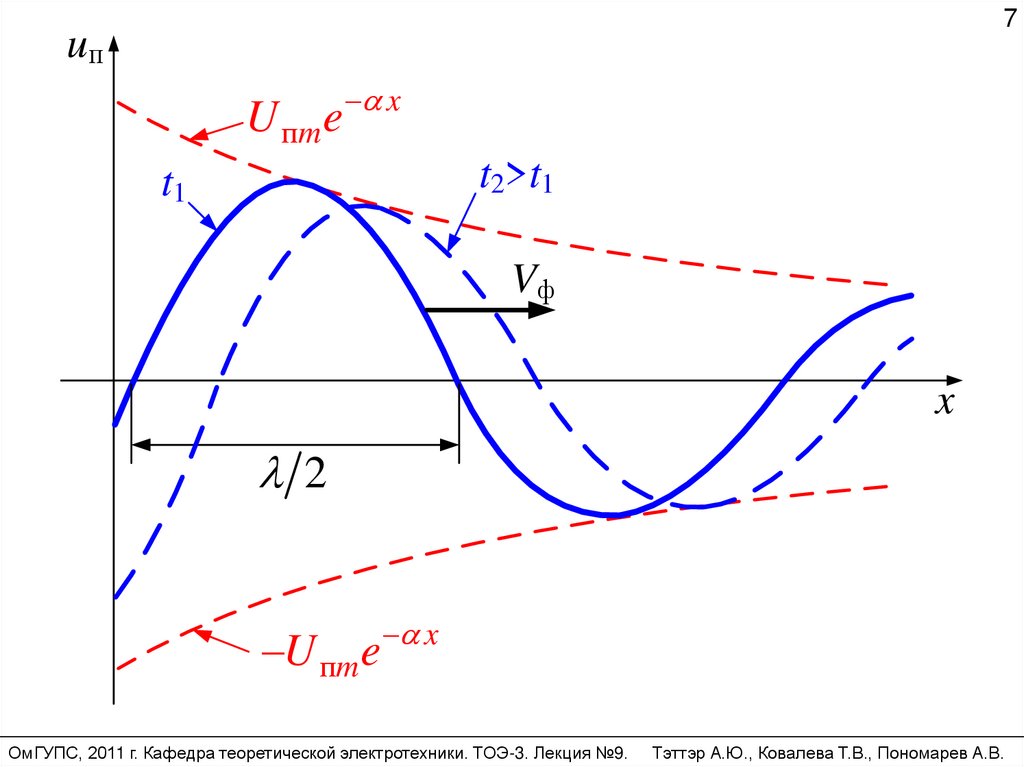
x
Функция uп e U пm sin( t п x )
есть математическое выражение прямой волны,
которая является затухающей синусоидой по
координате х.
6
Это распределение не является стационарным.
С течением времени оно непрерывно перемещается
по координате х вдоль линии от начала к концу.
Степень затухания прямой волны uп вдоль линии
определяет множитель e x .
Фаза прямой волны uп при фиксированном
моменте времени изменяется на единице длины
линии на величину .
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

7.

7
uп
U пm e
x
t2>t1
t1
Vф
x
2
U пm e x
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

8.

Убывание амплитуды прямой волны вдоль линии
обусловлено потерями в линии,
8
изменение фазы – конечной скоростью ее
распространения.
x
Функция uо e U оm sin( t о x )
представляет собой бегущую волну напряжения,
перемещающуюся в обратном направлении:
от конца линии к ее началу.
Она называется обратной волной.
Результирующее напряжение в любой точке
линии в любой момент времени формируется в
виде суммы прямой и обратной волн.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

9.

uо
9
x
U оm e
Vф
y=ℓ–x
x
U оm e
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

10.

В соответствии с выражением (5)
10
1
1
x
x
U
(
x
)
(
U
I
Z
)
e
(
U
I
Z
)
e
;
1
1
в
1
1
в
2
2
1
1
x
x
I ( x)
(U1 I1Z в )e
(U1 I1Z в )e
2Zв
2Zв
для получения выражения мгновенных значений
тока необходимо:
– комплексы прямой и обратной волн разделить
на волновое сопротивление;
– изменить знак второй составляющей.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

11.

В этом случае мгновенное значение тока будет
11
иметь вид:
i ( x, t ) iп ( x, t ) io ( x, t )
e
x
I пm sin( t пi x)
x
e I оm sin( t оi x),
где I пm
U оm
U пm
;
; I оm
Zв
Zв
пi п arg Z в ;
оi о arg Z в .
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

12.

В отличие от напряжения прямая и обратная
волны тока не складываются, а вычитаются.
Общий характер имеют соотношения
12
u uп uо ;
i iп iо .
Волны напряжения и тока перемещаются вдоль
линии с определенной скоростью.
В однородной линии скорость неизменна по всей
длине.
При анализе синусоидальных процессов в линиях
за скорость движения волны принимают фазовую
скорость Vф.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

13.

Это скорость перемещения вдоль линии какой-то
фиксированной фазы.
Фаза функции sin( t п x) будет постоянна,
13
если не изменяется ее аргумент t п x .
Для нахождения Vф это условие представляется
в виде:
t п x const
и берется производная по времени от обеих
частей равенства:
dx
0.
dt
dx
.
Фазовая скорость Vф
dt
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

14.

Вторым параметром бегущих волн является
длина волны λ – расстояние между двумя
ближайшими точками, разность фаз колебаний в
которых равна 2 :
2 ;
2
14
.
2 f 1 2
VфT T
.
f
Параметр , определяемый из выражения
(r0 j L0 )( g 0 j C0 ) j ,
называется коэффициентом фазы.
Он характеризует изменение фазы напряжения
или тока на единице длины линии.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

15.

Фазовая скорость волн напряжения и тока
в воздушных линиях близка к скорости
распространения электромагнитного поля в вакууме
(чистом в воздухе), которая составляет величину
Vф
1
0 0
15
3 10 м/с 3 10 км/с,
8
5
т. е. равна скорости света в вакууме с.
1
Ф
7 Гн
Здесь 0
и 0 4 10
9
м
4 9 10 м
соответственно диэлектрическая и магнитная
проницаемости вакуума (воздуха).
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

16.

Фазовая скорость в кабелях (в диэлектрике)
16
В электрических кабелях применяется изоляция
из различных диэлектриков.
Их диэлектрическая проницаемость больше ε0,
поэтому для кабелей
Vф
1
r 0 0
может быть значительно меньше величины
c = 3·105 км/с.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

17.

Вторичные параметры однородной линии
(коэффициент распространения и волновое
сопротивление Zв) определяются по формулам:
17
(r0 j L0 )( g 0 j C0 ) j ;
Zв
r0 j L0
.
g 0 j C0
Эти параметры входят в основные соотношения,
описывающие процессы в линиях, и выражаются
через первичные параметры r0, L0, g0 и C0.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

18.

18
Коэффициент распространения γ характеризует
изменение амплитуд (действующих значений) и
фаз напряжения (тока) прямой (обратной) волны на
единице длины линии.
Его действительная часть называется
коэффициентом затухания,
а мнимая часть – коэффициентом фазы.
Выразим коэффициент распространения через
напряжения прямой волны.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

19.

19
Комплексы прямой волны для начала (x=0) и
конца (x=ℓ) линии определяются как
U п ( x) U п1e
x
U1пр U п1;
;
U 2пр U п1e
.
Отношение этих величин
U1пр
U 2пр
1
e
e
позволяет выразить коэффициент распространения
в следующем виде:
1
ln
U1пр
U 2пр
.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

20.

Пусть далее
20
U1пр U1пр e
j 1пр
;
U 2пр U 2пр e
j 2пр
.
где U1пр и U2пр – действующие значения прямой
волны соответственно в начале и в конце линии,
а β1пр и β2пр – начальные фазы.
1
j ln
1
ln
U1пр
U 2пр
U1пр
U 2пр
1
j ( 1пр 2пр ),
1
, Нп/км; ( 1пр 2пр ), рад/км.
Затуханию в один непер соответствует изменение
амплитуд или действующих значений напряжения
(тока) прямой волны в e = 2,718 раза.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

21.

21
Произведение – собственное затухание
линии – определяется по формуле:
ln
U1пр
U 2пр
, Нп.
Произведение 1пр 2пр полное
изменение фазы прямой волны напряжения
(тока) по длине всей линии.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.

22.

22
Волновое сопротивление
Zв
r0 j L0
j в
Z вe
g 0 j C0
определяется отношением комплексов
одноименных волн напряжения и тока в любой
точке линии:
U п ( x) U о ( x)
Zв
.
I п ( x) I о ( x)
В однородной линии эта величина не зависит от
координаты х.
ОмГУПС, 2011 г. Кафедра теоретической электротехники. ТОЭ-3. Лекция №9.
Тэттэр А.Ю., Ковалева Т.В., Пономарев А.В.