Первообразная. Понятие первообразной

1. Первообразная

2.

3. Устно: Найдите производную функции

4. Какую функцию можно вставить в скобку, чтобы равенство было верным : 

Какую функцию можно вставить в скобку,
чтобы равенство было верным :

5. Понятие первообразной

Функцию F(x) называют первообразной для
функции f(x) на интервале (a; b), если на нем
производная функции F(x) равна f(x):
F ( x ) f ( x )
Операцию, обратную дифференцированию
называют интегрированием.

6.

Является ли F(x) первообразной для функции f(x)
1.f(x) = 2x; F(x) = x2
F (x)= (x2) = 2x = f(x)
2.f(x) = – sin x; F(x) = сos x
F (x)= (cos x) = – sin x = f(x)
3.f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F (x)= (2x3 + 4x) = 6x2 + 4 = f(x)

7. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ СФОРМУЛИРУЕМ В ВИДЕ ТЕОРЕМЫ

Если функция F(х) одна из
первообразных функции f(х),
то любая первообразная этой
функции получается прибавлением к
F(х) некоторой постоянной: F(х) + С.
Графики функций у = F(х) + С
получаются из графика у = F(х)
сдвигом вдоль оси Оу

8.

Примеры
1. f(x) = 2x; F(x) = x2 -11
2. f(x) = – sin x;
F(x) = сos x+45
3. f(x) = 6x2 + 4;
F(x) = 2x3 + 4x-222

9.

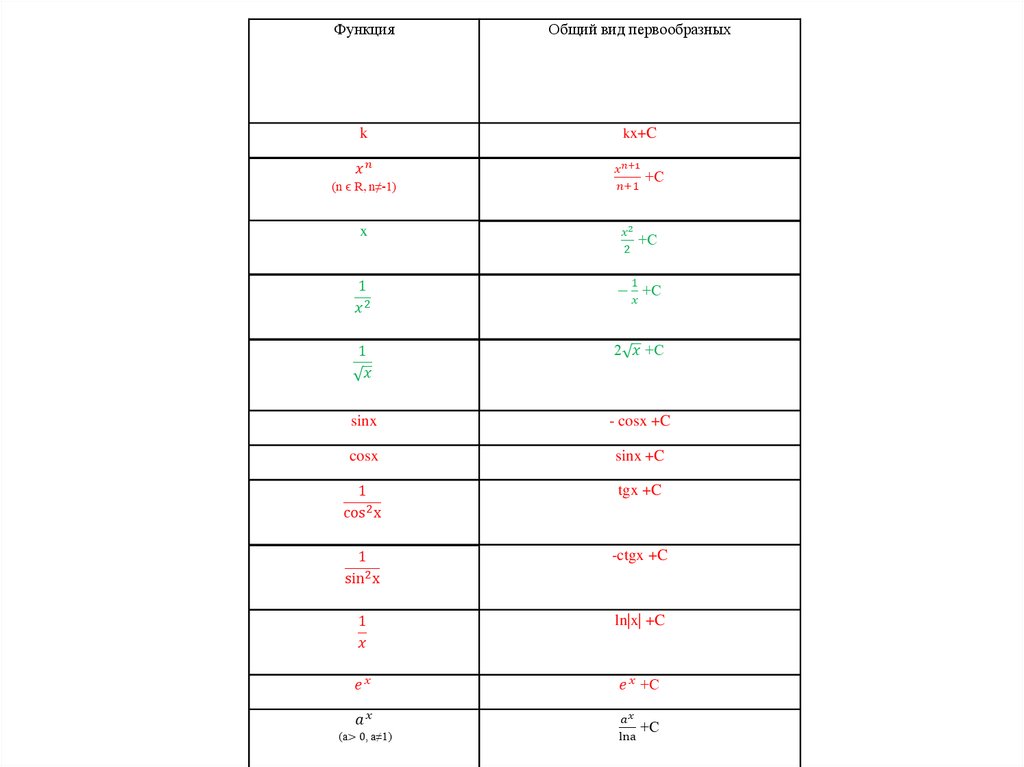
Функция
Общий вид первообразных
k
kx+C
x
sinx
- cosx +C
cosx
sinx +C
tgx +C
-ctgx +C
ln|x| +C

10. Правила нахождения первообразных

11.

12. Пример

13.

14. Пример

Найдите общий вид первообразных для функций:
f(х) = 5cos x
Решение
F(х) = 5sin x + C

15. Пример