Свойство и признак описанного четырёхугольника

1.

Свойство и признак
описанного четырёхугольника

2.

5
2
1
4
3
7
6

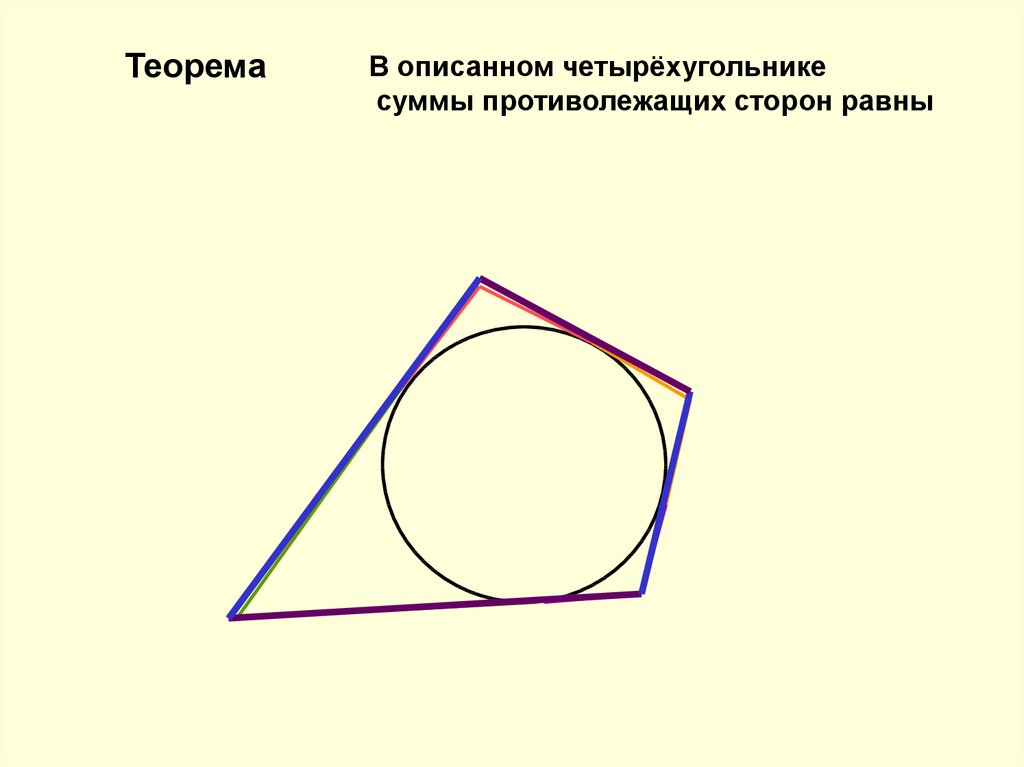
3. Теорема

В описанном четырёхугольнике
суммы противолежащих сторон равны

4.

Теорема
C
L
M
B
Дано : ABCD – описанный
четырёхугольник,
К, L, M, N - точки касания
K
D
AB + CD
N
A
Доказать: AB + CD = AD + BC
Доказательство.
= ( AK + KB ) + ( CM + MD )
AB + CD = (AK + KB) + (CM + MD).
BL)
(LС
AD + BC AD=+(BC
+ (+ (BL
BL ++ LC)
LC= )(AN
) ++ ND)
( LC + ND )
AN=+(AN
ND+ )ND)
= (+AN
+ +BL
По свойству касательных, проведённых из одной точки:
= AN, KB =BL,
CM = LC, MD =из
ND.
По свойствуAK
касательных,
проведённых
одной точки:
Cледовательно : AB + CD = AD + BC
AK = AN , KB = BL , CM = LC , MD = ND .
Следовательно: AB + CD = AD + BC

5.

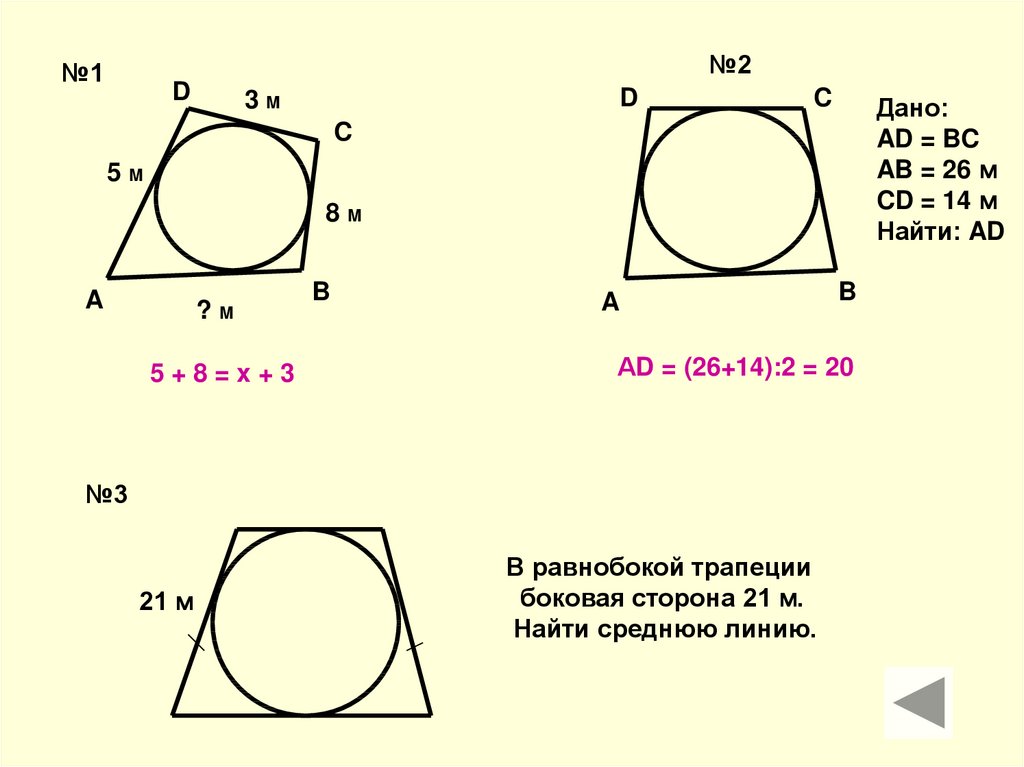
№2
№1
D
D
3M
C
Дано:
AD = BC
AB = 26 м
CD = 14 м
Найти: AD
C
5M
8M
A
?M
5+8=x+3
B
A
АD = (26+14):2 = 20
№3
21 м
B
В равнобокой трапеции
боковая сторона 21 м.
Найти среднюю линию.

6.

№1
9м
Можно ли вписать окружность
в четырёхугольник со сторонами
9 м, 14 м и 13 м, 10 м?
10 м
13 м
Да, так как 9 + 14 = 13 + 10
14 м
№2
1м
D
C
АК = (9 – 1) : 2 = 4
AD = 5
3м
AB + DC = AD + BC
B
A
K
9м
Можно ли вписать окружность в равнобокую трапецию
с основаниями 1 м и 9 м и высотой 3 м ?

7.

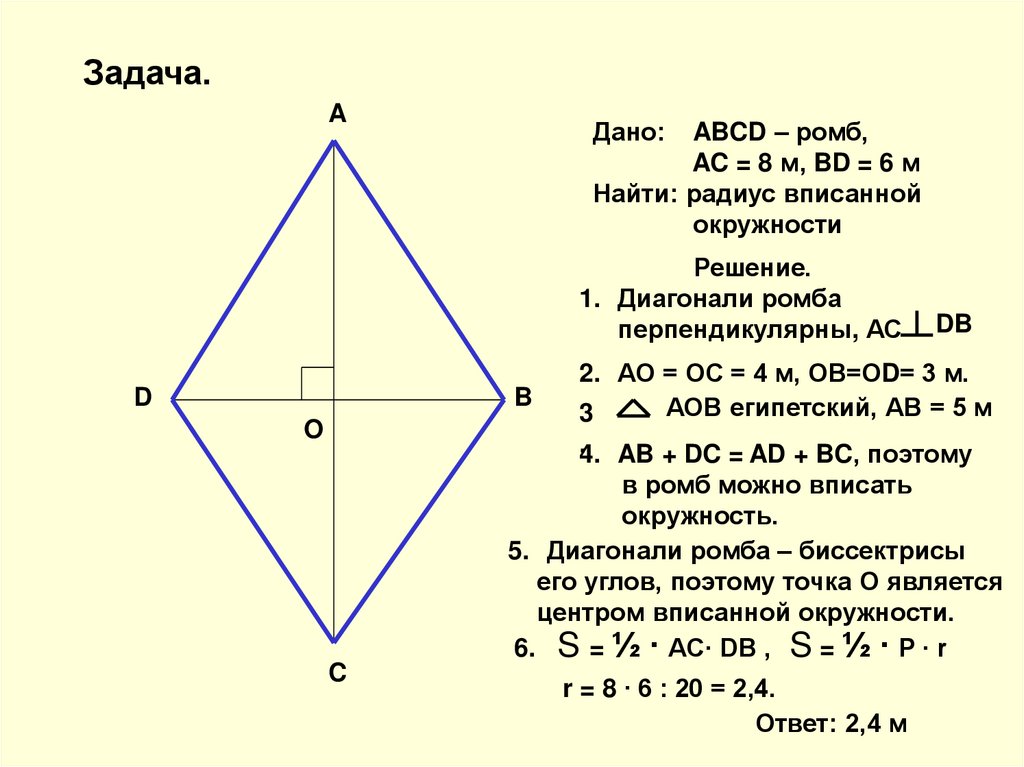
Задача.
A
Дано:
ABCD – ромб,
AC = 8 м, BD = 6 м
Найти: радиус вписанной
окружности
Решение.
1. Диагонали ромба
перпендикулярны, АС
D
B
O
C
DB
2. АО = ОС = 4 м, ОВ=ОD= 3 м.
АОВ египетский, АВ = 5 м
3
.4. AB + DC = AD + BC, поэтому
в ромб можно вписать
окружность.
5. Диагонали ромба – биссектрисы
его углов, поэтому точка О является
центром вписанной окружности.
6. S = ½ ∙ AC∙ DB , S = ½ ∙ P ∙ r
r = 8 ∙ 6 : 20 = 2,4.
Ответ: 2,4 м

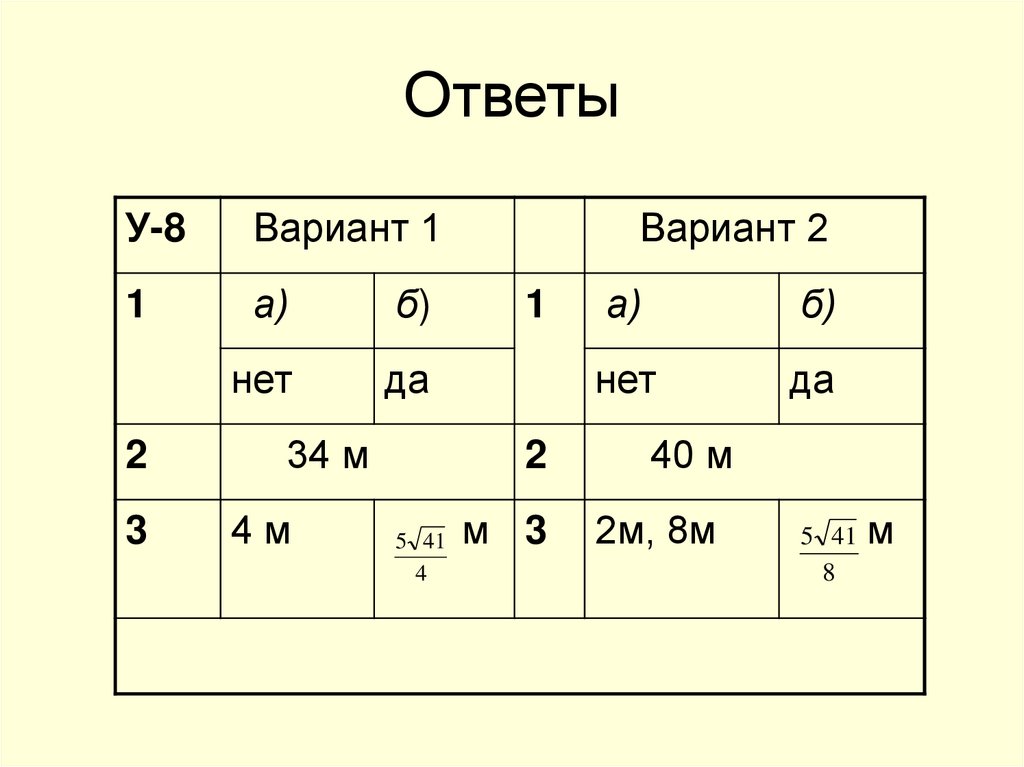
8. Ответы

У-8
Вариант 1
1
а)
б)
нет
да
2
3
34 м
4м
Вариант 2
1
2
5 41
4
м 3
а)
б)
нет
да
40 м
2м, 8м
5 41
8
м