Числовые промежутки

1.

Числовые промежутки

2.

2
1) a b 0,18; 5)a b 3,2 ; 9)a b 1 3 ;
a b
a b
a b
1
2n
2) a b
; 6)a b 1 5 ; 10)a b 1 ;
15
b
a
a
b
a
b
2
3)b a 0,42; 7)a b 3 1; 11)a b 1
a b
a b
a b
2 n 1
;
4)a b 3,2 ; 8)a b 2 5 ; 12)a b 2 2 .
a b
a b
a b
2
2
2n

3.

1) a - b
2) a - c
3) b - c
4) c - b
Ответ: 4.
1) xy
2) (x – y)y
3) ( y – x)y
4) (y – x)x
Ответ: 3.

4.

r
q
p
x
1) p - r
2) p - q
3) r - q
4) ни одна из них.
Ответ: 3.
a
b
с
x
1) a - b
2) c - b
3) a - c
4) ни одна из них.
Ответ: 2.

5.

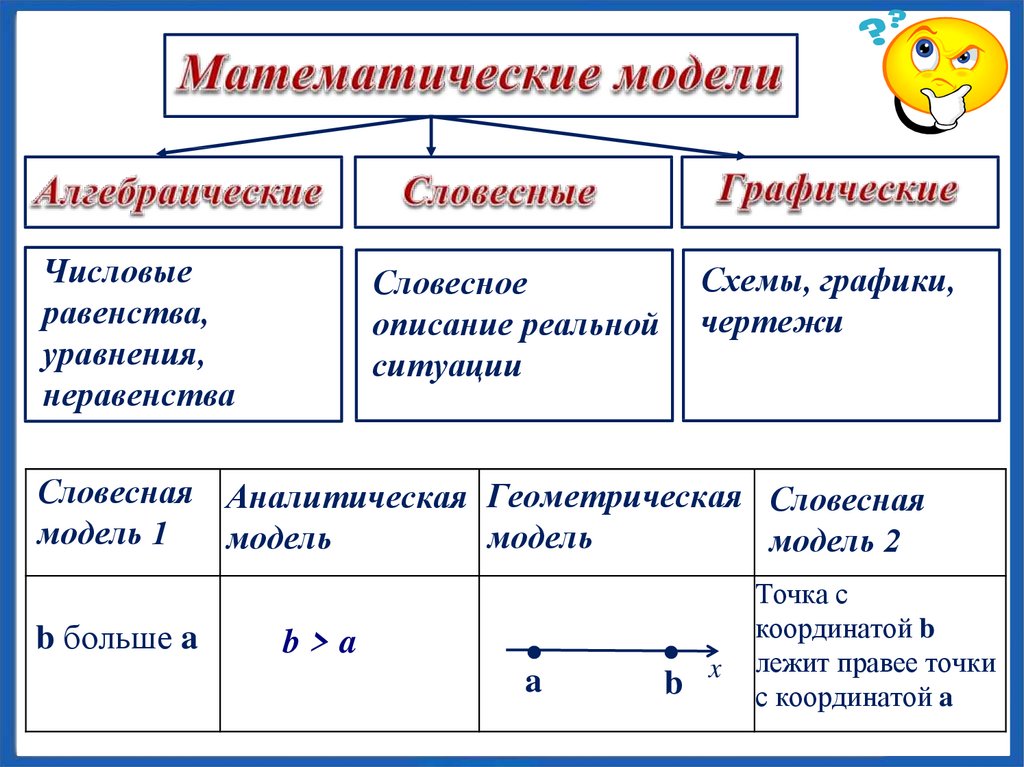
Числовые
равенства,
уравнения,
неравенства
Словесное
описание реальной
ситуации
Схемы, графики,
чертежи
Словесная Аналитическая Геометрическая Словесная
модель 1
модель
модель
модель 2
b больше a
b>a
a
b x
Точка с
координатой b
лежит правее точки
с координатой a

6.

;
a
x
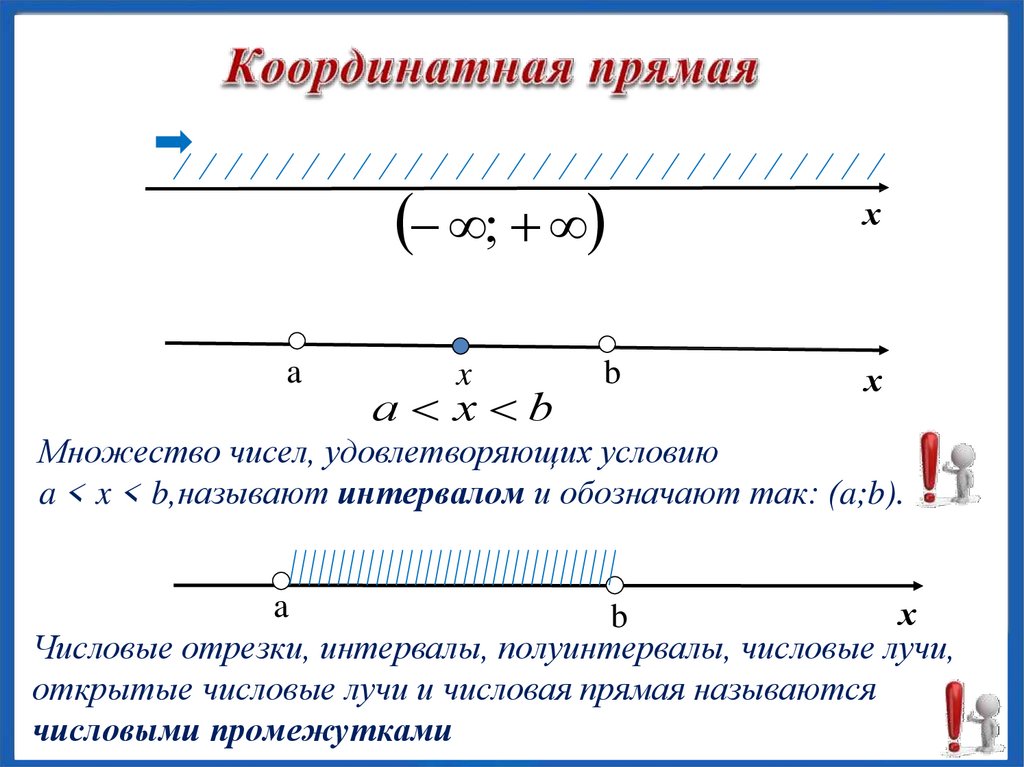
a x b
b
х
х
Множество чисел, удовлетворяющих условию
a < x < b,называют интервалом и обозначают так: (a;b).
a
х
b
Числовые отрезки, интервалы, полуинтервалы, числовые лучи,
открытые числовые лучи и числовая прямая называются
числовыми промежутками

7.

Таблица числовых промежутков
Геометрическая модель
х
a
х
a
a
a
a
Обозначение
Название
числового
промежутка
Аналитическая
модель
(a; )
Открытый луч
х a
a;
Луч
х a
( ; a )
Открытый луч
х a
a
х
a
х
; a
х
( a; b )
Интервал
a x b
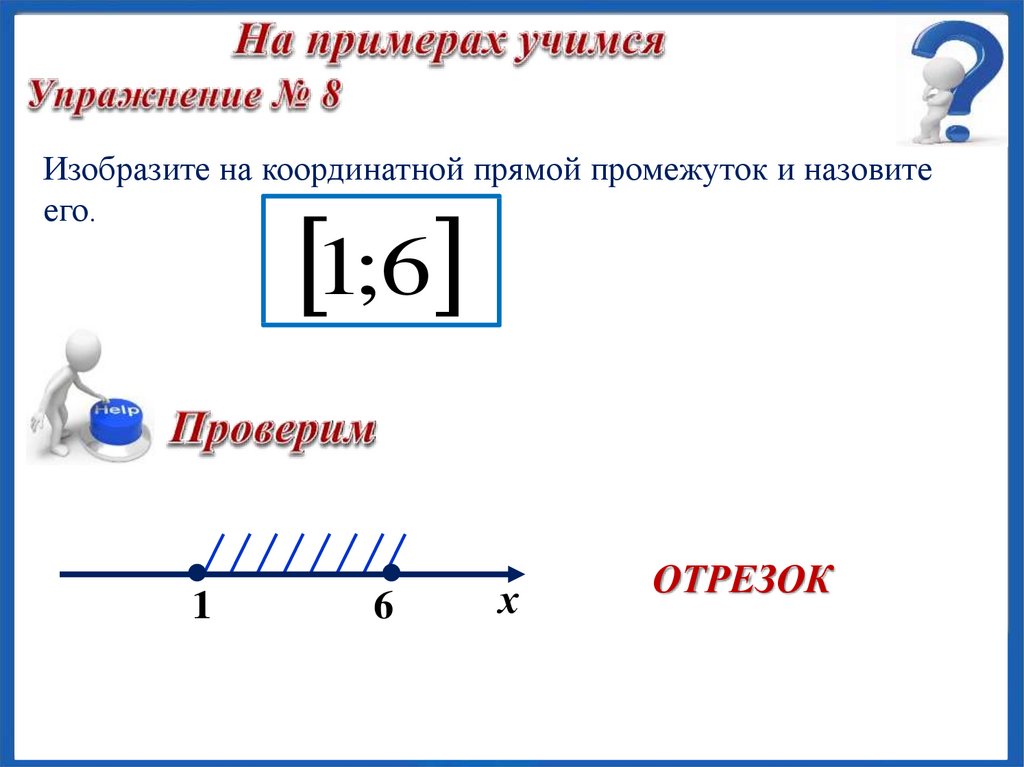
a; b
Отрезок
a x b
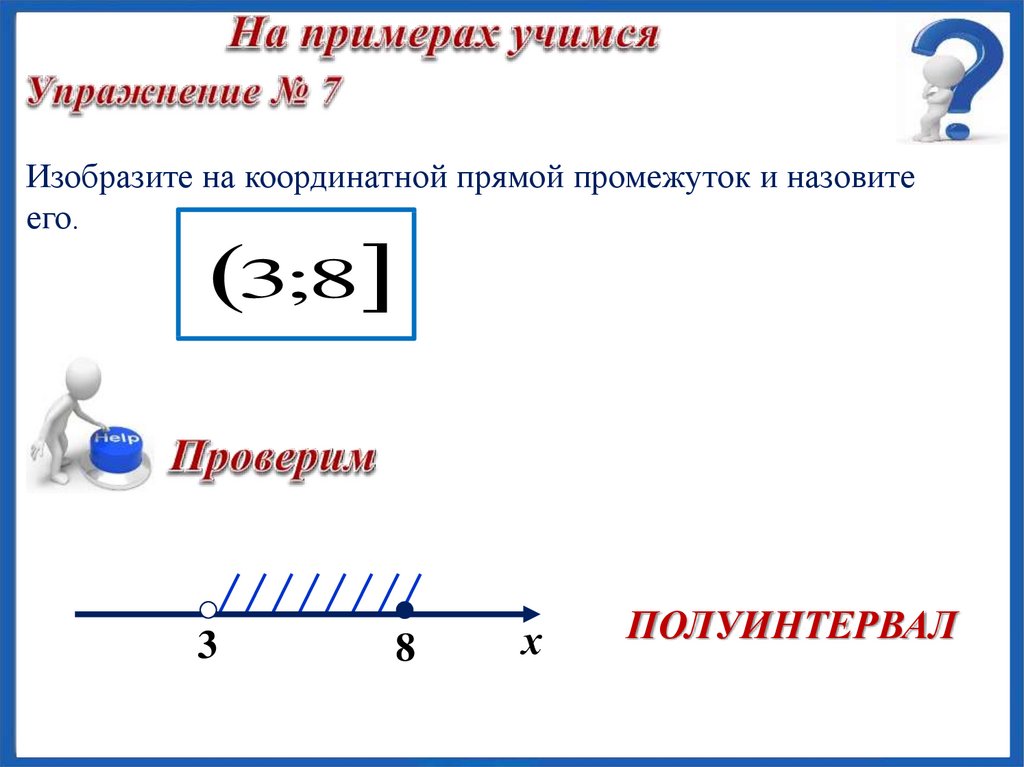
(a; b
Полуинтервал
a x b
b
b
b
х
х
Луч
х a

8.

Нестрогие
≤, ≥
Строгие
<, >
;
( ; )