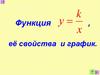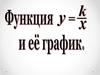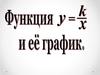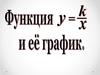Похожие презентации:
Обратная пропорциональность и ее график
1. Домашнее задание
П. 50, 51,№1246,
№1253
2.
Обратная пропорциональность и ее график3. О п р е д е л е н и е
ОпределениеОбратной пропорциональностью
называется функция, которую
можно задавать формулой вида
где х – независимая переменная,
k – не равное нулю число.
4. Свойства функции
1х 0
Областью определения функции является
множество всех чисел, отличных от нуля.
2
k 0 у 0
Областью значений функции является
множество всех чисел, отличных от нуля.
5.
Построим по точкам график функцииЧем больше точек, том точнее график функции. Здесь таблица разбита на две части (для
положительных и отрицательных х). Можно объединить в одну таблицу.
Постройте график данной функции
6.
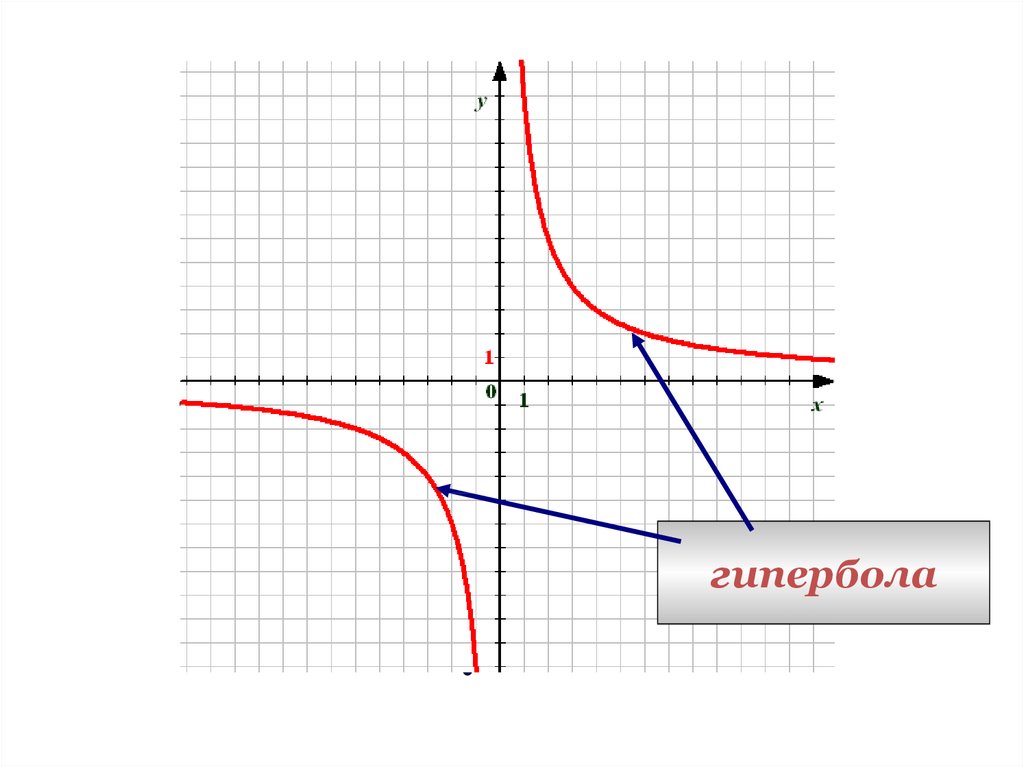
7.
гипербола8.
1.Область определенияD ( у ) ; 0 0 ;
у
2. Область значений
E ( у ) ; 0 0;
3. у > 0, если х 0 ;
у < 0, если х
; 0
4 Функция не
ограничена ни сверху,
ни снизу.
1
-3 -2 -1 0 1 2 3
-1
5. унаим.= НЕТ
унаиб.= НЕТ
6. Непрерывность
Претерпевает разрыв при х = 0.
х
9.
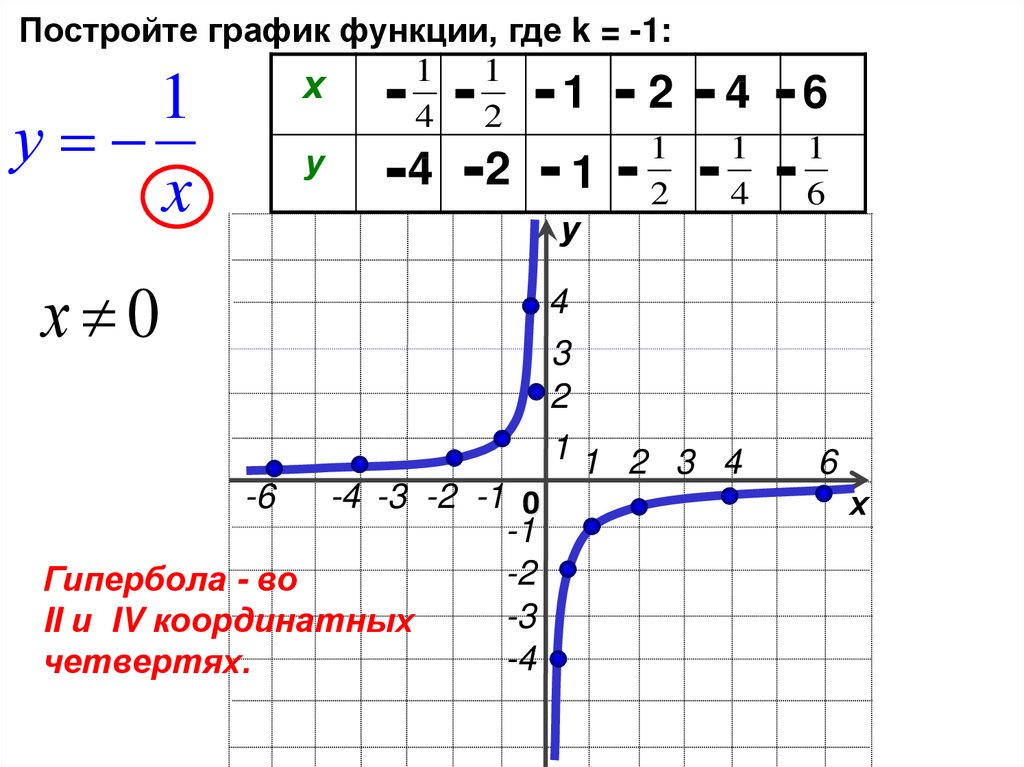
Постройте график функции, где k = -1:1
1
х
1 2
4
2
1
у
4 2 1 2
у
- - - - - 4 -6
1
1
- - - - -4 -6
1
у
x
х 0
4
3
2
11 2 3 4
-6
-4 -3 -2 -1 0
-1
-2
Гипербола - во
-3
II и IV координатных
-4
четвертях.
6
х
10.
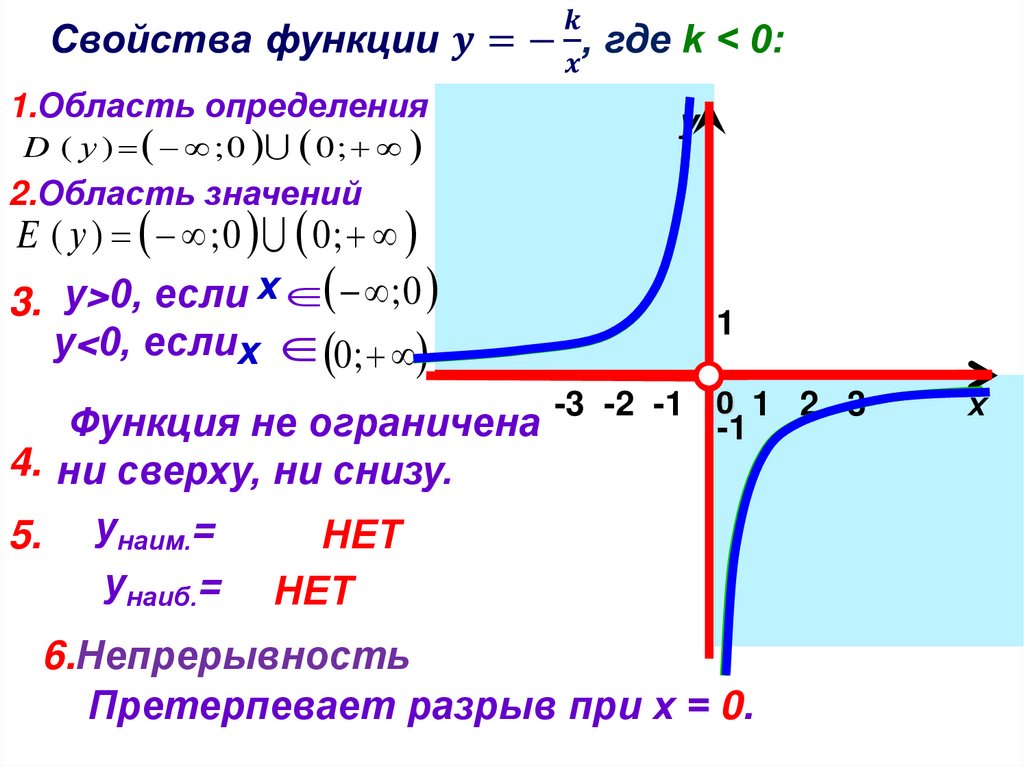
1.Область определенияD ( у ) ; 0 0 ;
у
2.Область значений
E ( у ) ; 0 0;
3. у>0, если х ; 0
у<0, если 0 ;
1
х
-3 -2 -1 0 1 2 3
Функция не ограничена
-1
4. ни сверху, ни снизу.
5. унаим.=
НЕТ
унаиб.= НЕТ
6.Непрерывность
Претерпевает разрыв при х = 0.
х
11.
Задача:Задайте функцию обратной пропорциональности, если ее график
проходит через точку (1; 3):
( 1; 3 )
х
у
Подставим координаты точки в формулу функции
обратной пропорциональности чтобы найти
коэффициент k.
k
3
1
k 3
12.
Задача:Задайте функцию обратной пропорциональности, если ее график
проходит через точку (2; -6):
( 2; -6 )
х
у
Подставим координаты точки в формулу функции
обратной пропорциональности чтобы найти
коэффициент k.









 Математика
Математика