Геометрический смысл определенного интеграла

1. Геометрический смысл определенного интеграла

Вычисление площади

2. Содержание

Интеграл и площадь (основные формулы)
Вычисление площадей (легкие случаи)
Задача 1 (использование симметрии)
Задача 2 (новая система координат)
Задача 3 (более трудный случай)
Площадь как способ вычисления интеграла

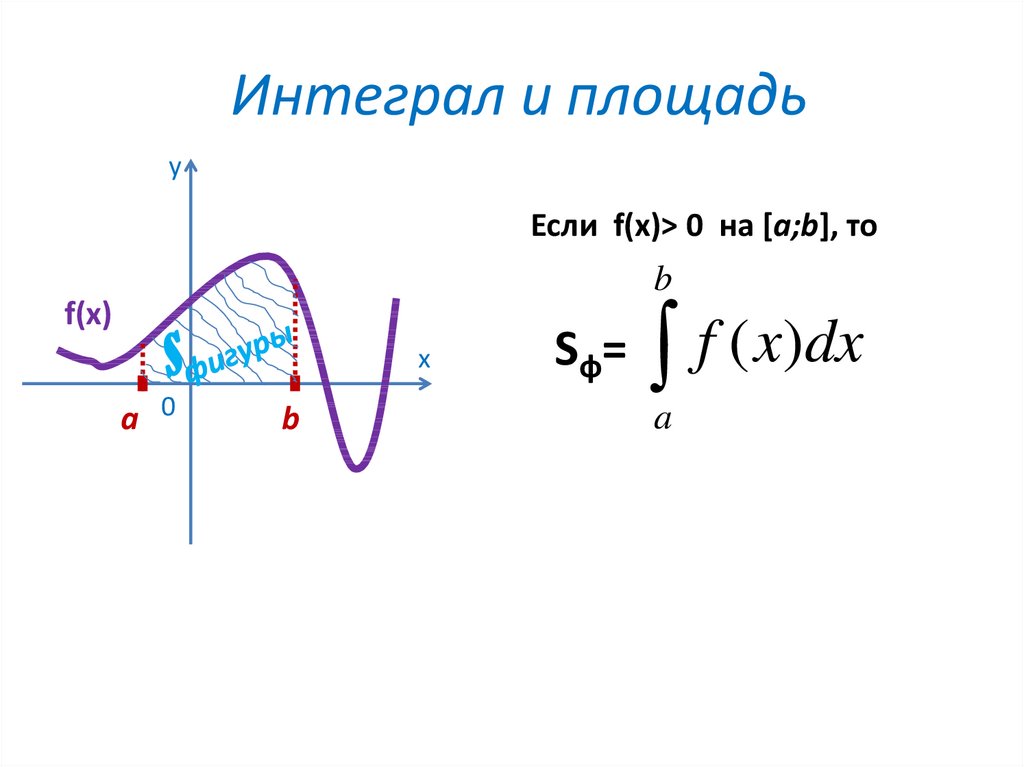
3. Интеграл и площадь

у
Если f(x)> 0 на [a;b], то
b
f(x)
х
а 0
b
Sф=
a
f ( x)dx

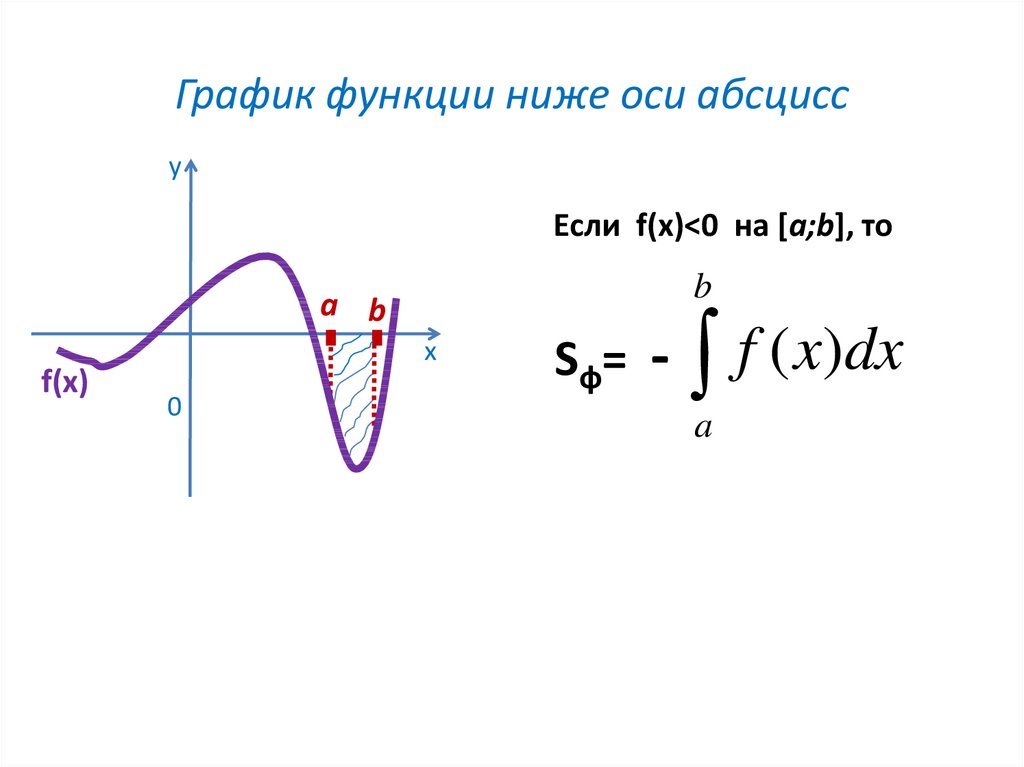
4. График функции ниже оси абсцисс

у
Если f(x)<0 на [a;b], то
b
а b
f(x)
х
0
Sф=
-
a
f ( x)dx

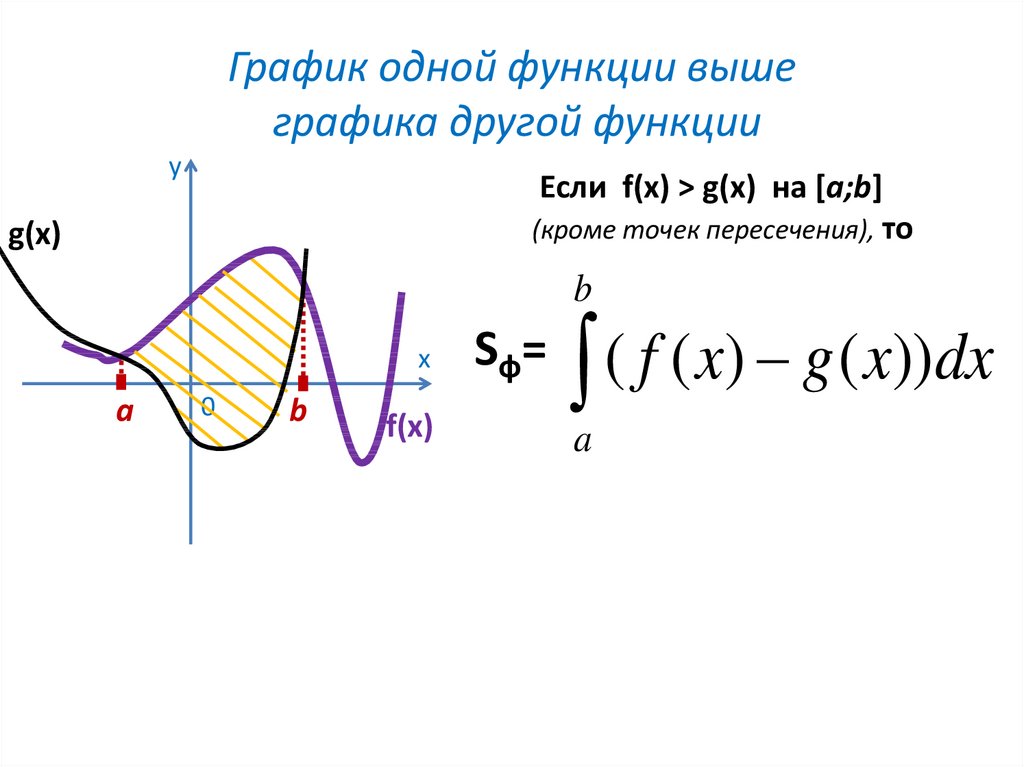
5. График одной функции выше графика другой функции

у
Если f(x) > g(x) на [a;b]
(кроме точек пересечения), то
g(x)
b
х
а
0
b
f(x)
Sф=
(
f
(
x
)
g
(
x
))
dx
a

6. Формула Ньютона - Лейбница

b
f ( x)dx F (b) F (a)
a
F(x) – одна из первообразных для f(x)

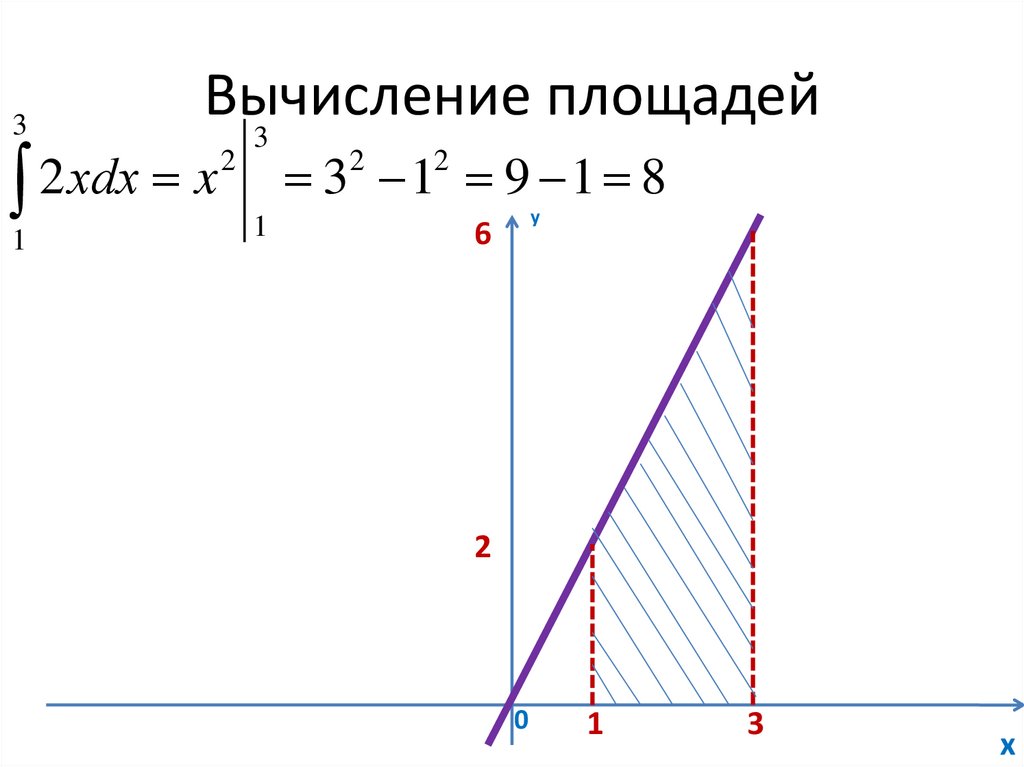
7. Вычисление площадей

3
Вычисление площадей
2 хdx x
1
2
3
1
3 1 9 1 8
2
2
у
6
2
0
1
3
х

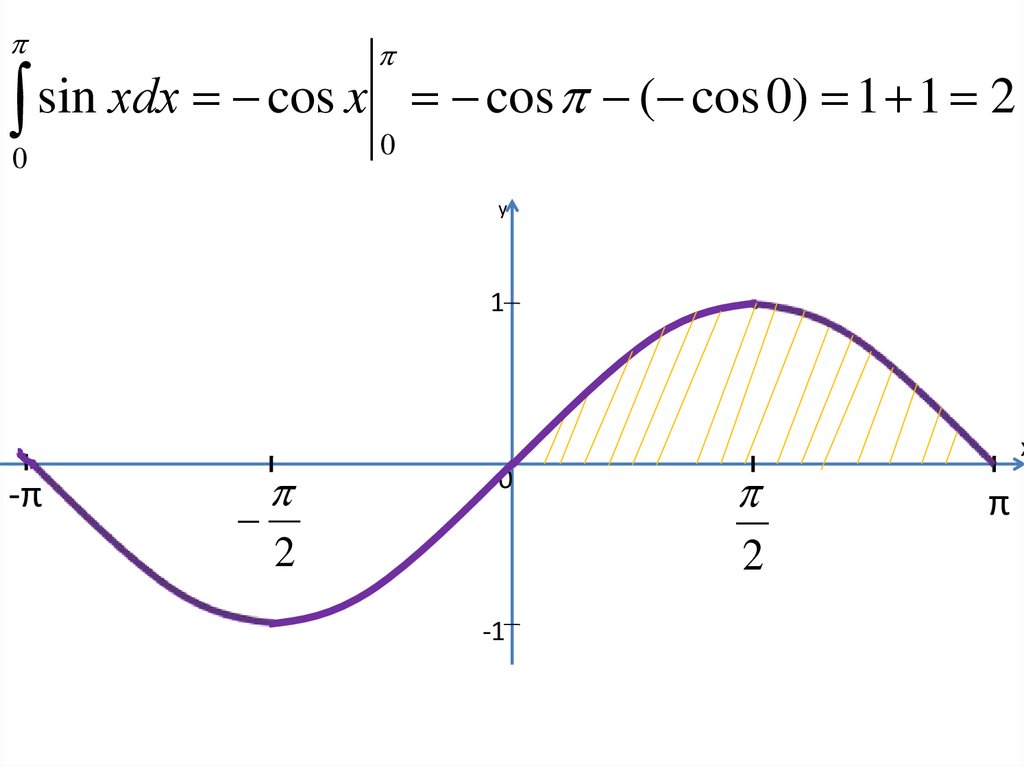
8.

0
0
sin
хdx
cos
x
cos
(
cos
0
)
1
1
2
y
1
-π
2
0
-1
2
x
π

9.

sin
хdx
2
0
2
y
sin
хdx
?
0
1
-π
2
0
-1
2
x
π

10.

0
2
sin
хdx
1
0
sin
хdx
?
y
1
-π
2
0
-1
2
x
π

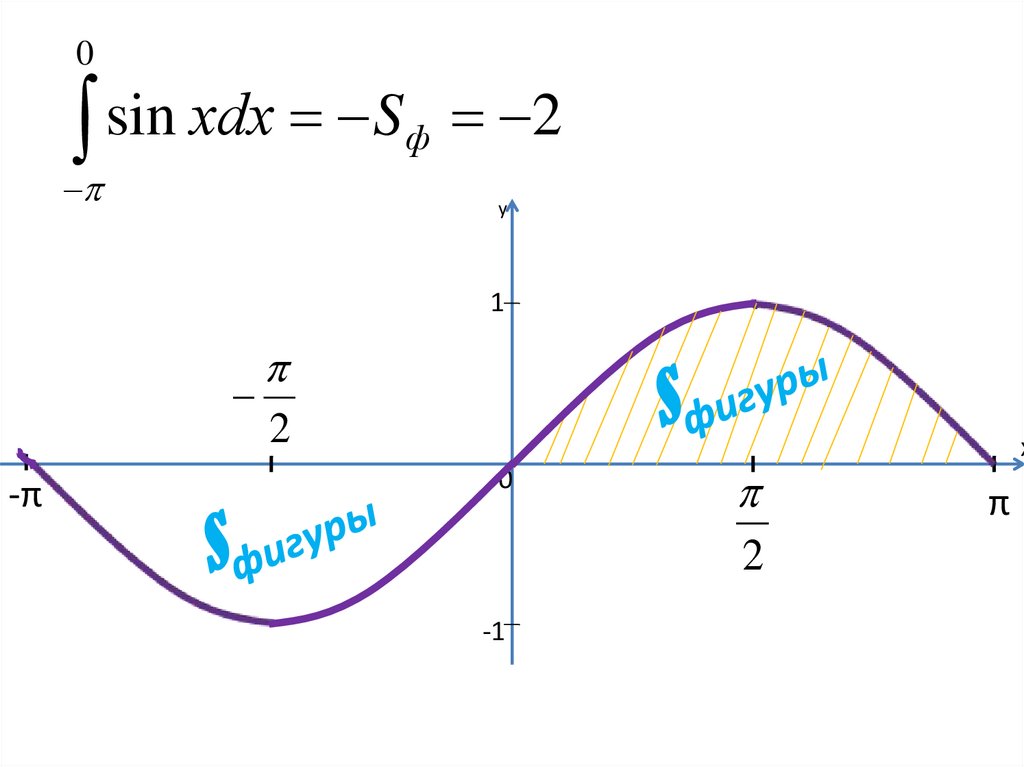
11.

0
sin
хdx
S
2
ф
y
1
2
-π
0
-1
2
x
π

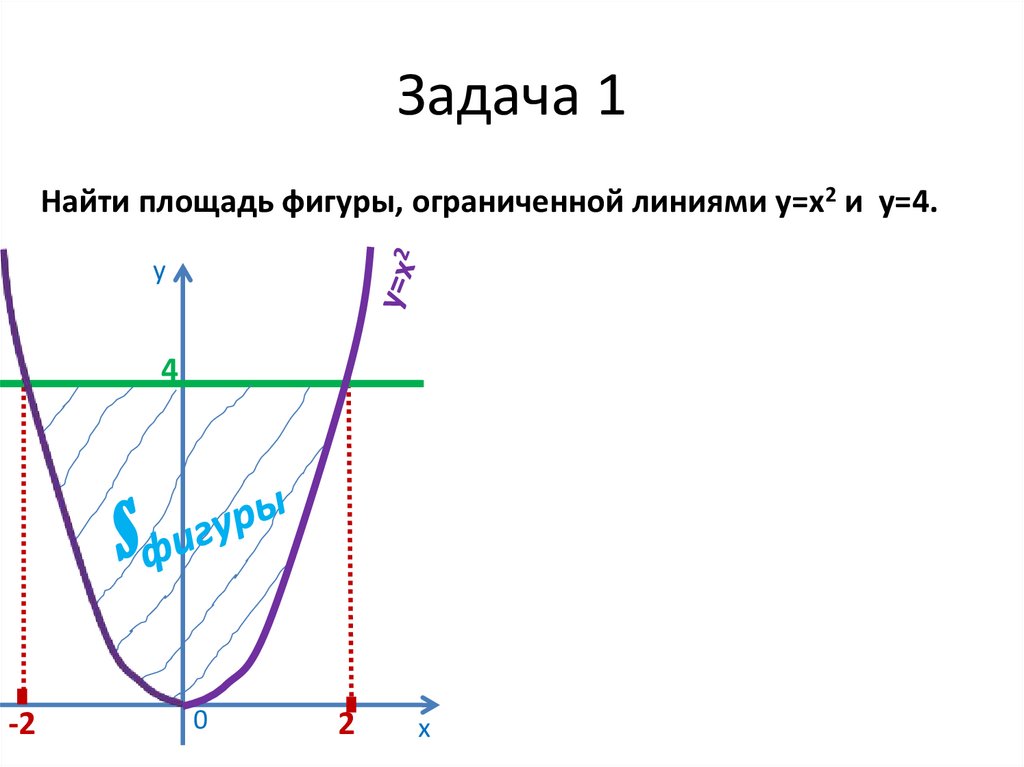
12. Задача 1

Найти площадь фигуры, ограниченной линиями у=х2 и у=4.
у
4
-2
0
2
х

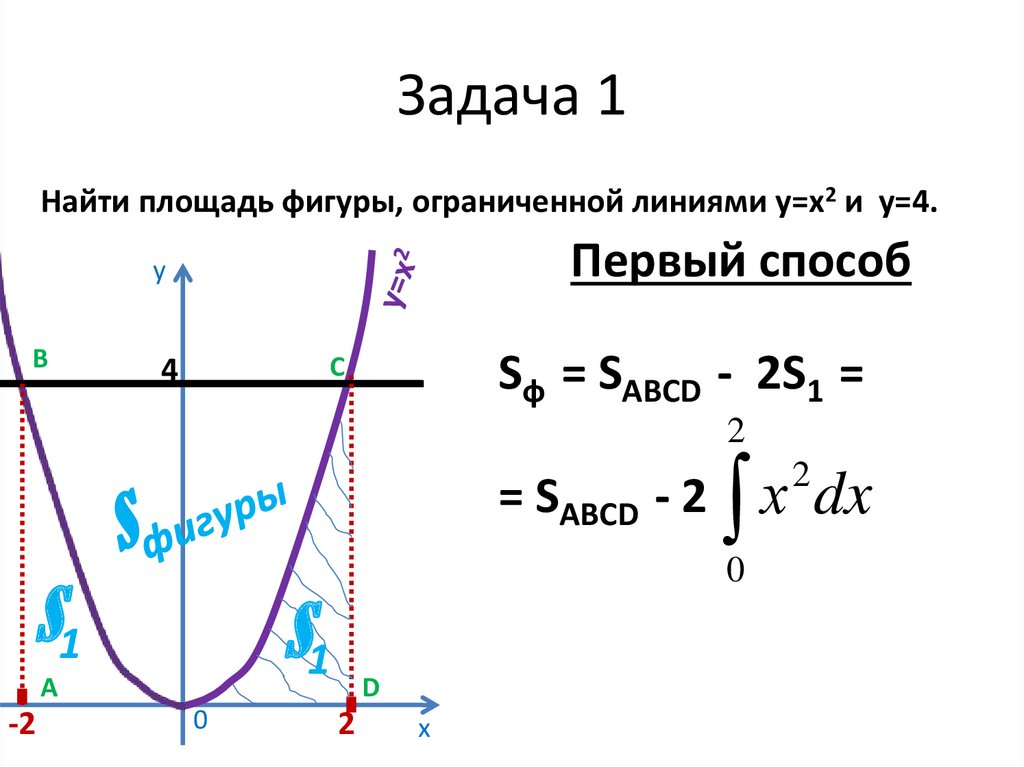
13. Задача 1

Найти площадь фигуры, ограниченной линиями у=х2 и у=4.
Первый способ
у
B
Sф = SABCD - 2S1 =
C
4
2
= SABCD - 2
S1
-2
0
S1
A
0
х
dx
2
D
2
х

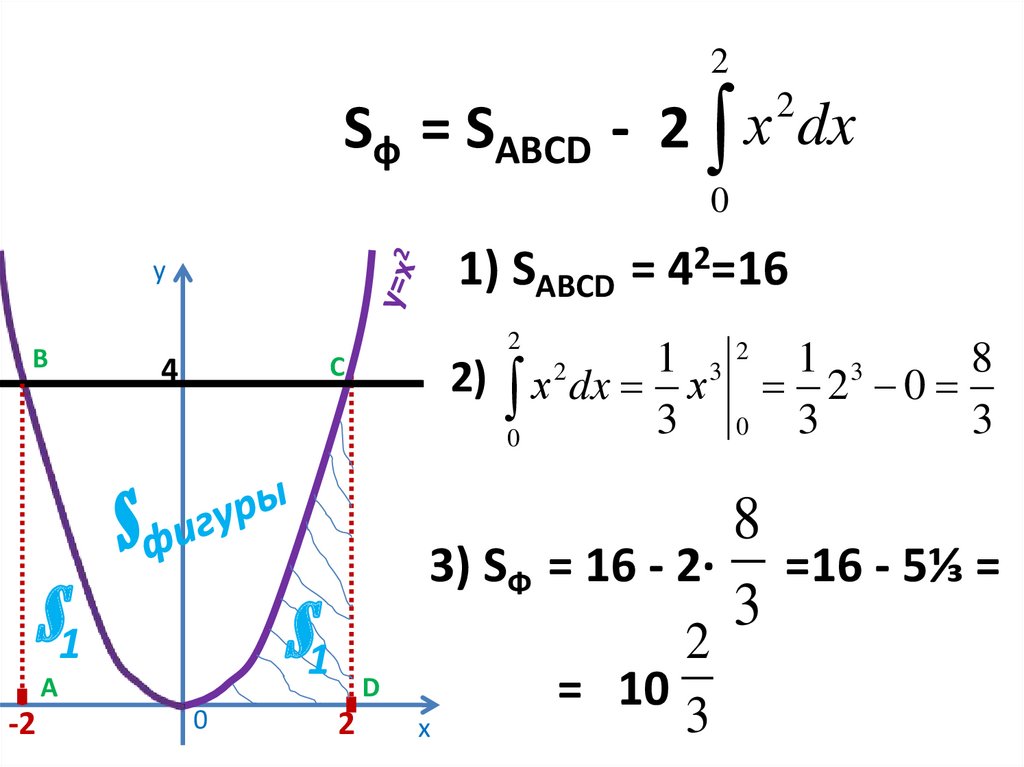
14. Sф = SABCD - 2

2
Sф = SABCD - 2 х dx
2
0
1) SABCD = 42=16
у
B
2
1
3
2) х dx х 1 23 0 8
0
3 0 3
3
C
4
S1
0
2
8
3) SФ = 16 - 2∙ =16 - 5⅓ =
3
S1
A
-2
2
D
2
х
2
= 10
3

15. Задача 1

Найти площадь фигуры,ограниченной линиями у=х2 и у=4.
Второй способ
у
Замечаем, что график у=4
выше графика у=х2 на [-2;2]
4
(кроме точек пересечения).
Тогда:
2
S ф (4 х 2 )dx
2
-2
0
2
х

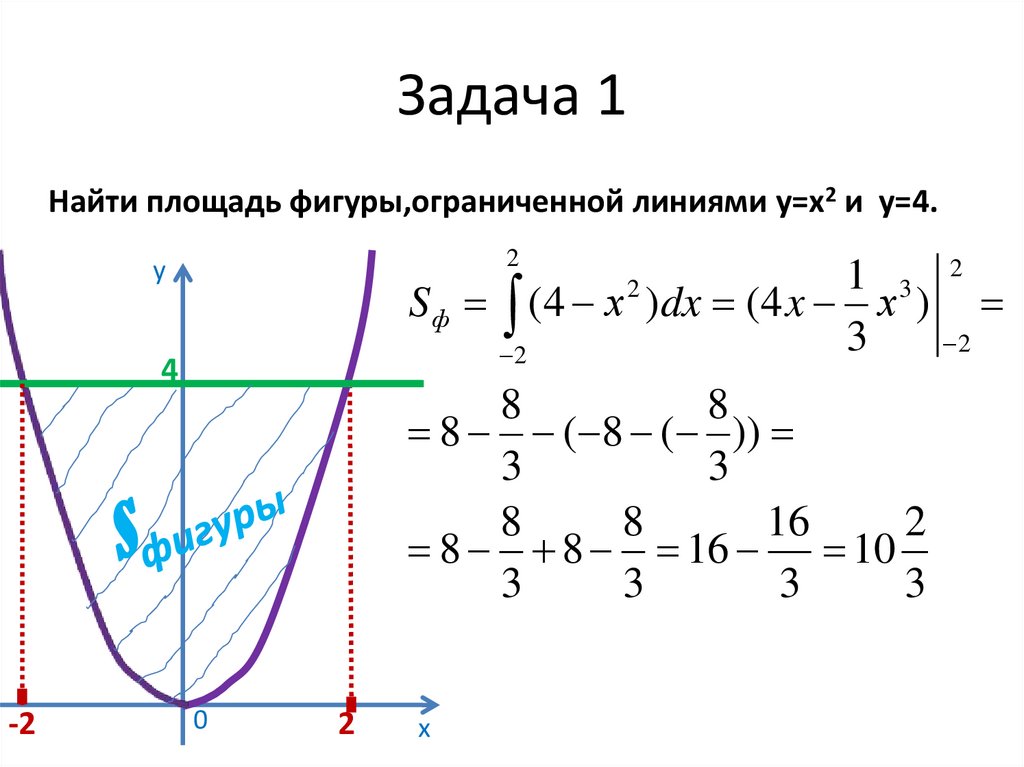
16. Задача 1

Найти площадь фигуры,ограниченной линиями у=х2 и у=4.
2
у
2
1
S ф (4 х 2 )dx (4 x х 3 )
3
2
2
4
-2
8
8
8 ( 8 ( ))
3
3
2
16
8
8
8 8 16 10
3
3
3
3
0
2
х

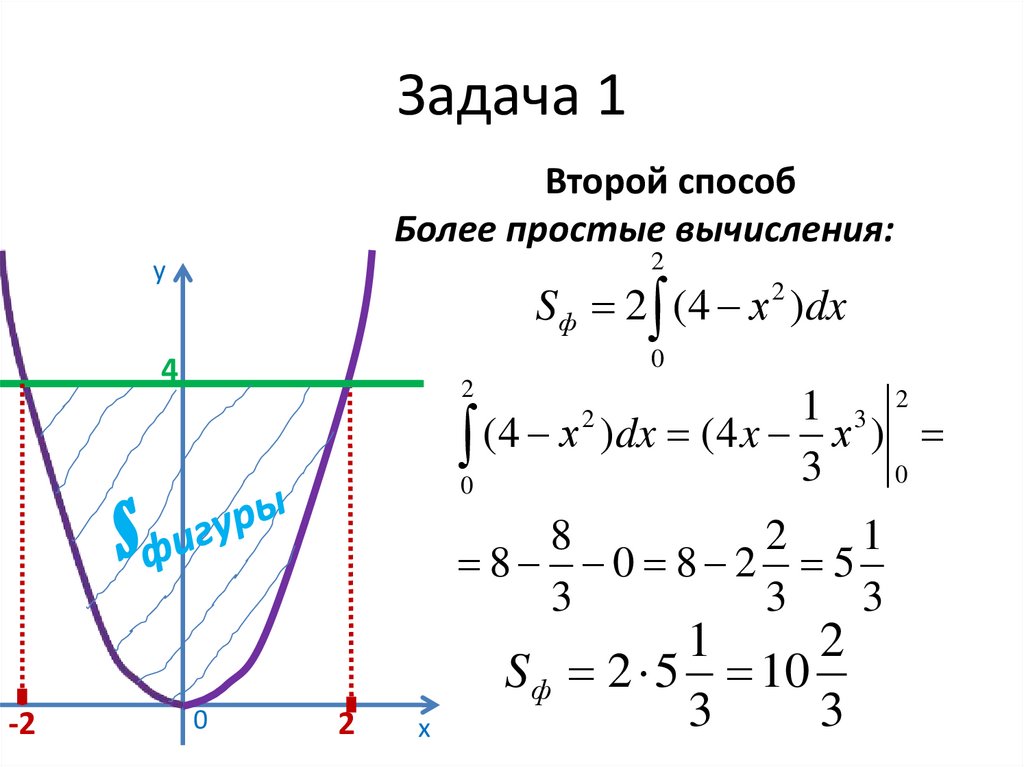
17. Задача 1

Второй способ
Более простые вычисления:
2
у
Sф 2 (4 х )dx
2
0
4
2
2
1
2
3
(
4
х
)
dx
(
4
x
х
)
0
3
0
8
2
1
8 0 8 2 5
3
3
3
-2
0
2
х
1
2
S ф 2 5 10
3
3

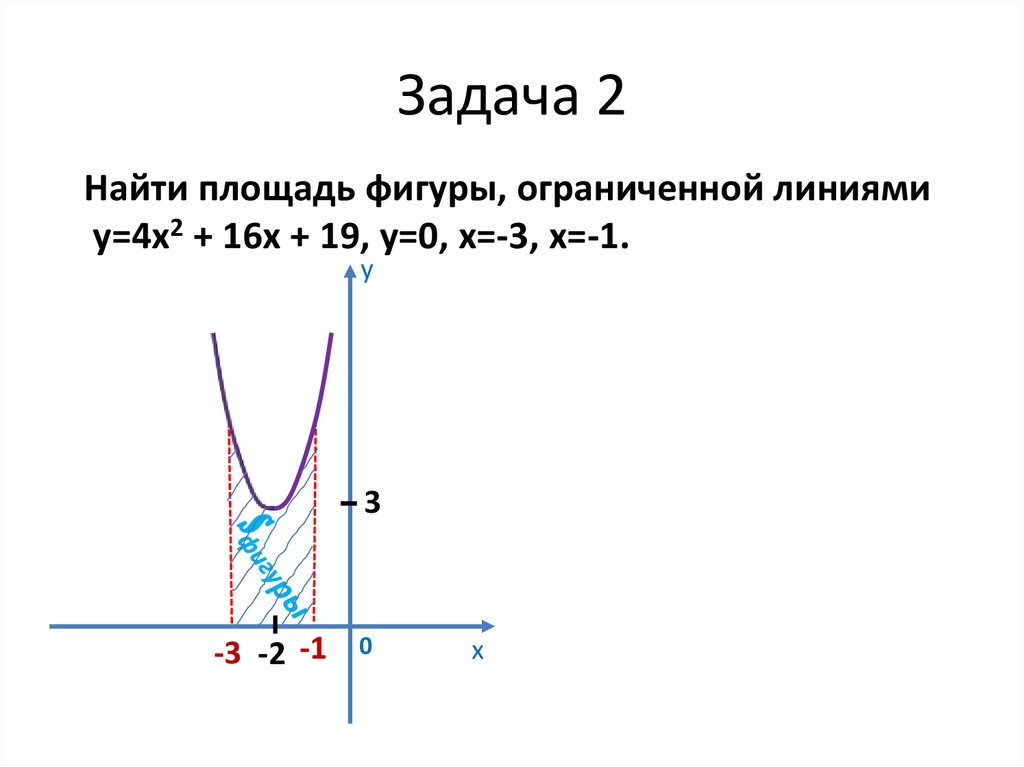
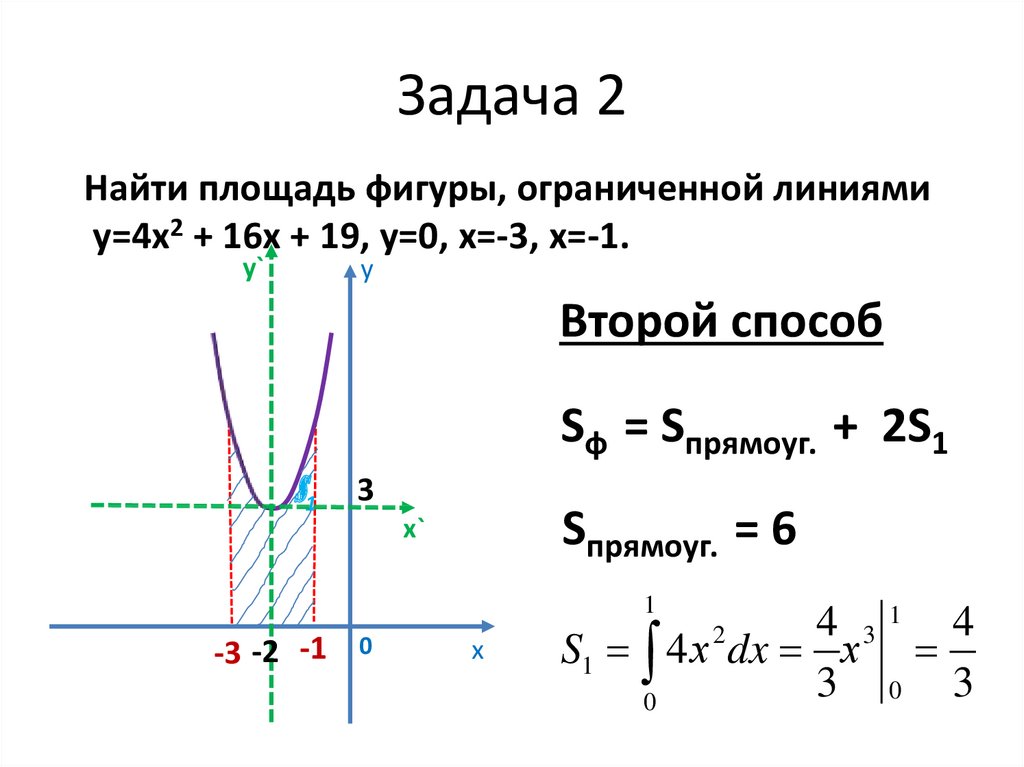
18. Задача 2

Найти площадь фигуры, ограниченной линиями
у=4х2 + 16х + 19, у=0, х=-3, х=-1.
у
3
-3 -2 -1
0
х

19. Задача 2

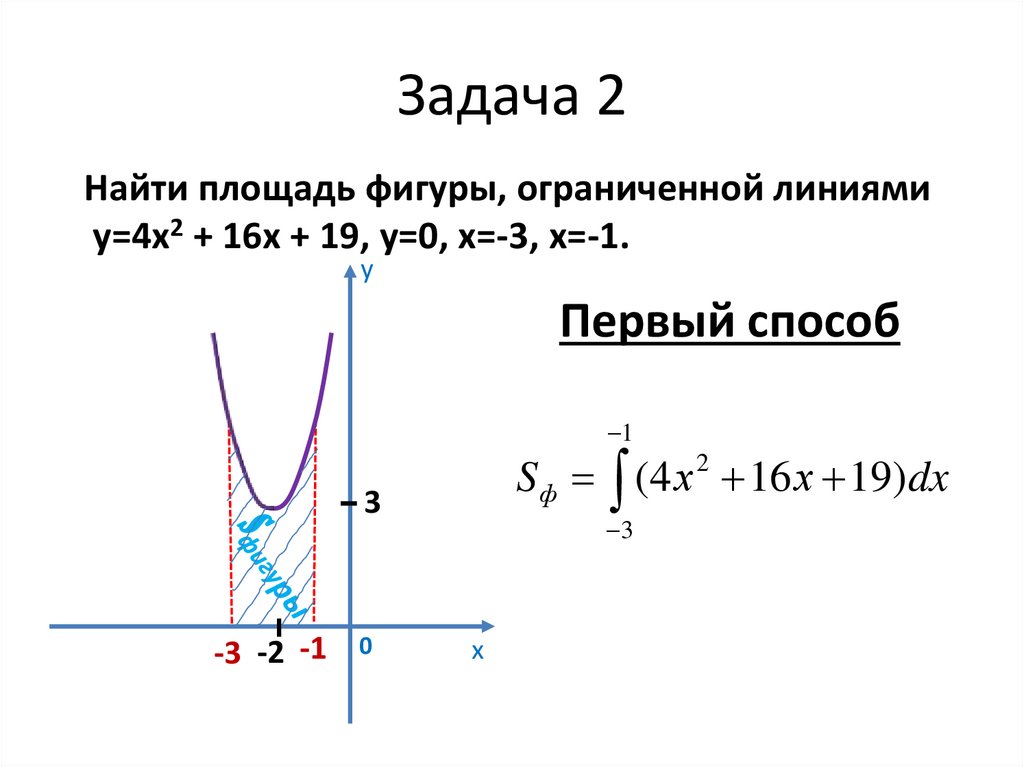
Найти площадь фигуры, ограниченной линиями
у=4х2 + 16х + 19, у=0, х=-3, х=-1.
у
Первый способ
1
S ф (4 х 16 х 19)dx
2
3
-3 -2 -1
0
3
х

20. Задача 2

1
1
4 3
2
S ф (4 х 16 х 19)dx ( х 8 х 19 х)
3
3
3
2
4
4 ( 27)
4
8 19 (
72 57) 11 36 15
3
3
3
2
8
3

21. Задача 2

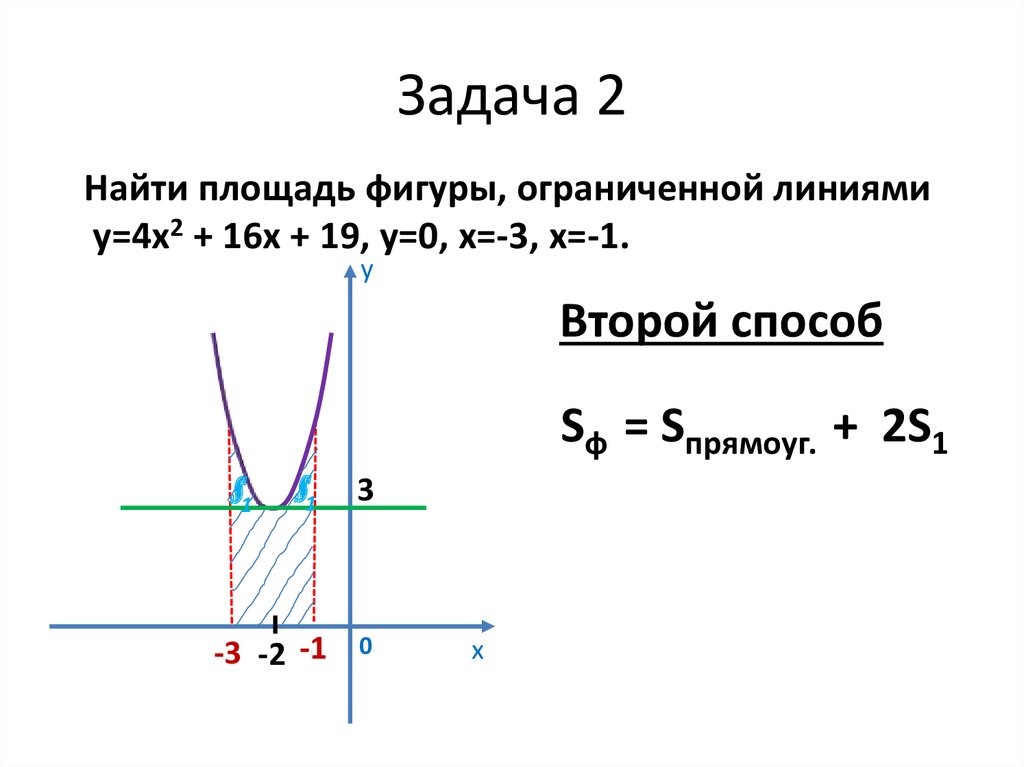
Найти площадь фигуры, ограниченной линиями
у=4х2 + 16х + 19, у=0, х=-3, х=-1.
у
Второй способ
Sф = Sпрямоуг. + 2S1
S1
S1
-3 -2 -1
3
0
х

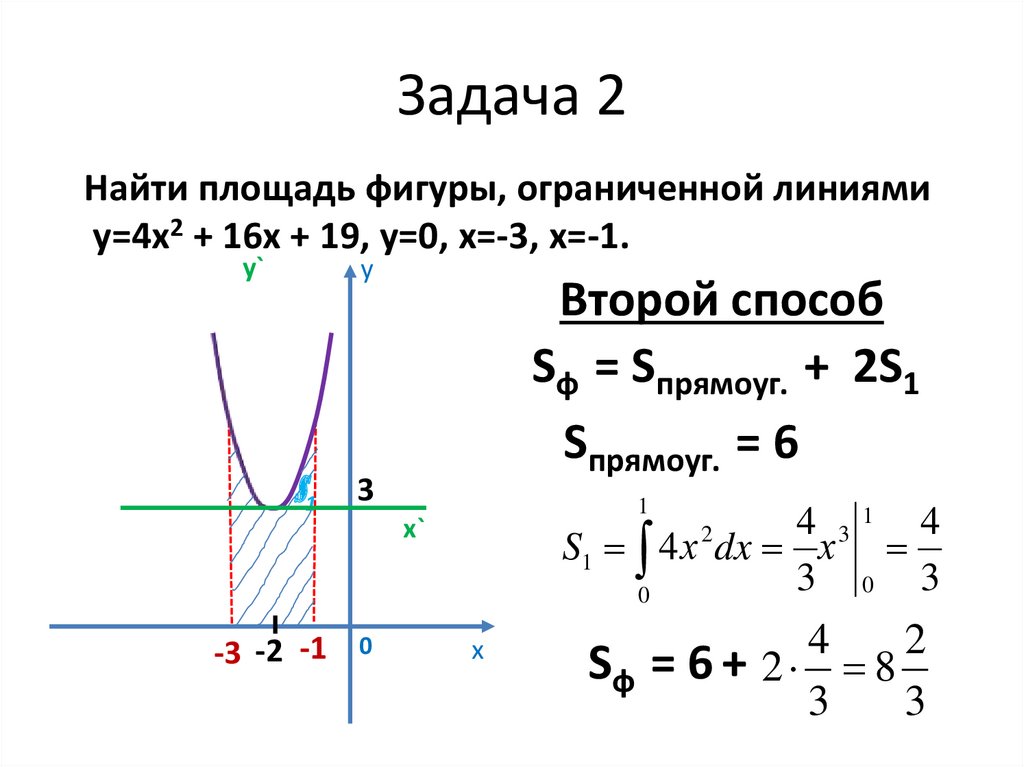
22. Задача 2

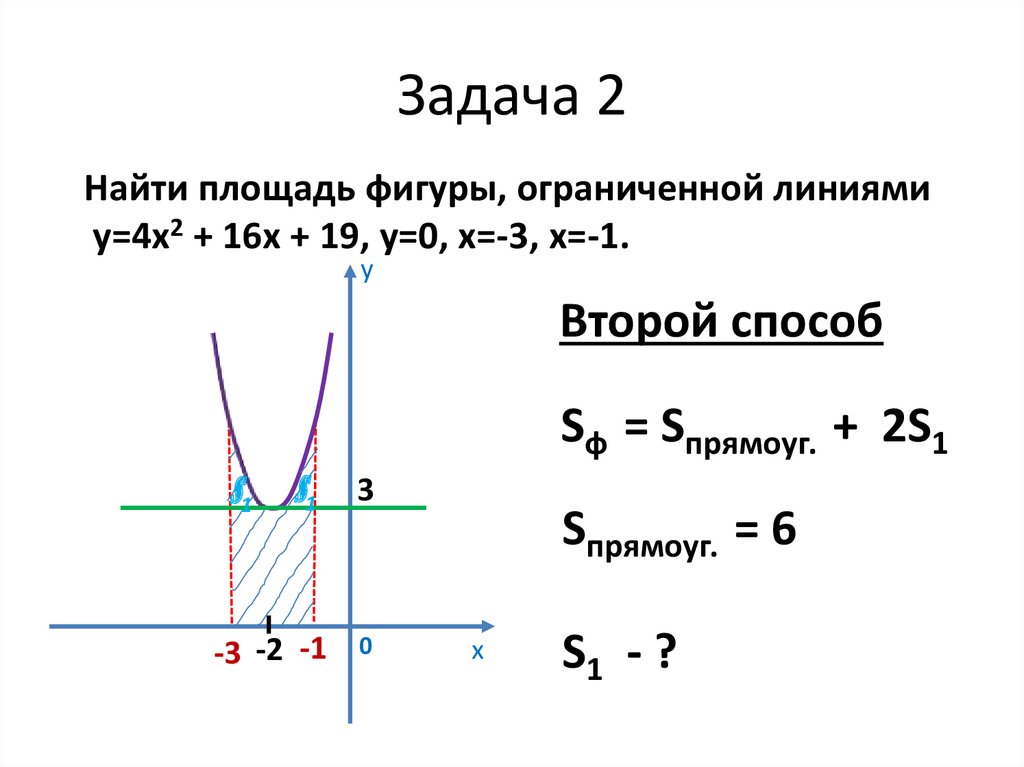
Найти площадь фигуры, ограниченной линиями
у=4х2 + 16х + 19, у=0, х=-3, х=-1.
у
Второй способ
Sф = Sпрямоуг. + 2S1
S1
S1
-3 -2 -1
3
0
Sпрямоуг. = 6
х
S1 - ?

23. Задача 2

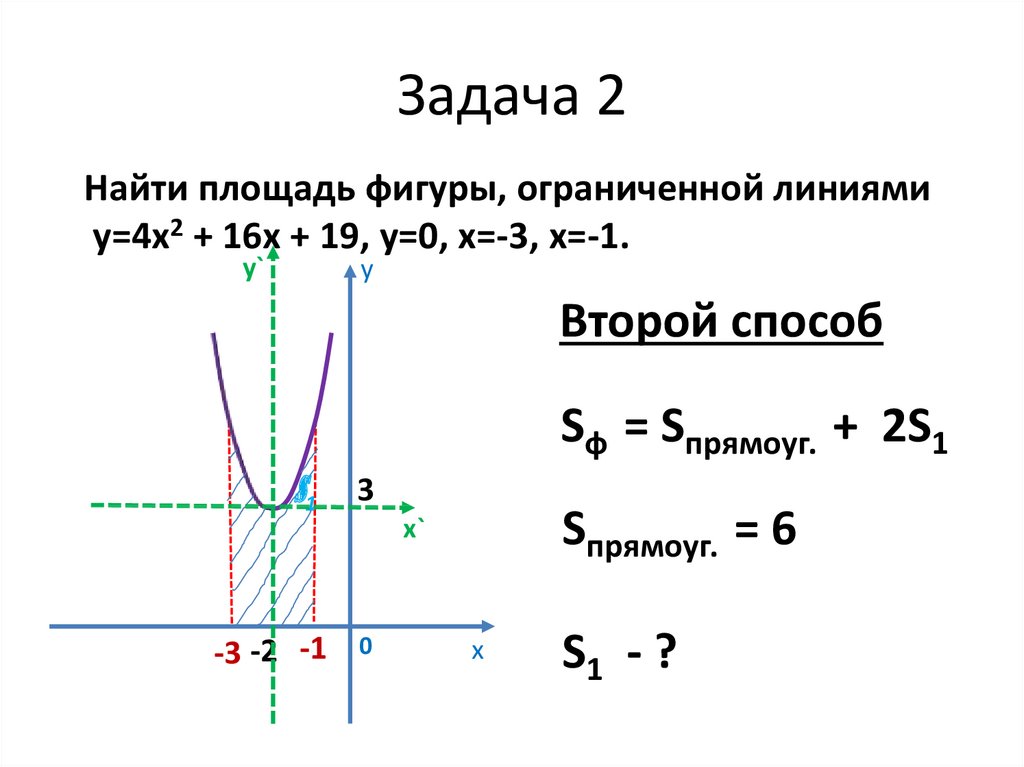
Найти площадь фигуры, ограниченной линиями
у=4х2 + 16х + 19, у=0, х=-3, х=-1.
y`
у
Второй способ
Sф = Sпрямоуг. + 2S1
S1
-3 -2 -1
3
Sпрямоуг. = 6
х`
0
х
S1 - ?

24. Задача 2

Найти площадь фигуры, ограниченной линиями
у=4х2 + 16х + 19, у=0, х=-3, х=-1.
y`
у
Второй способ
Sф = Sпрямоуг. + 2S1
S1
3
Sпрямоуг. = 6
х`
1
-3 -2 -1
0
х
4 31 4
S1 4 х dx х
3 0 3
0
2

25. Задача 2

Найти площадь фигуры, ограниченной линиями
у=4х2 + 16х + 19, у=0, х=-3, х=-1.
y`
у
S1
-3 -2 -1
Второй способ
Sф = Sпрямоуг. + 2S1
Sпрямоуг. = 6
3
1
1
4
4
2
3
S1 4 х dx х
3 0 3
0
х`
0
х
4
2
Sф = 6 + 2 8
3
3

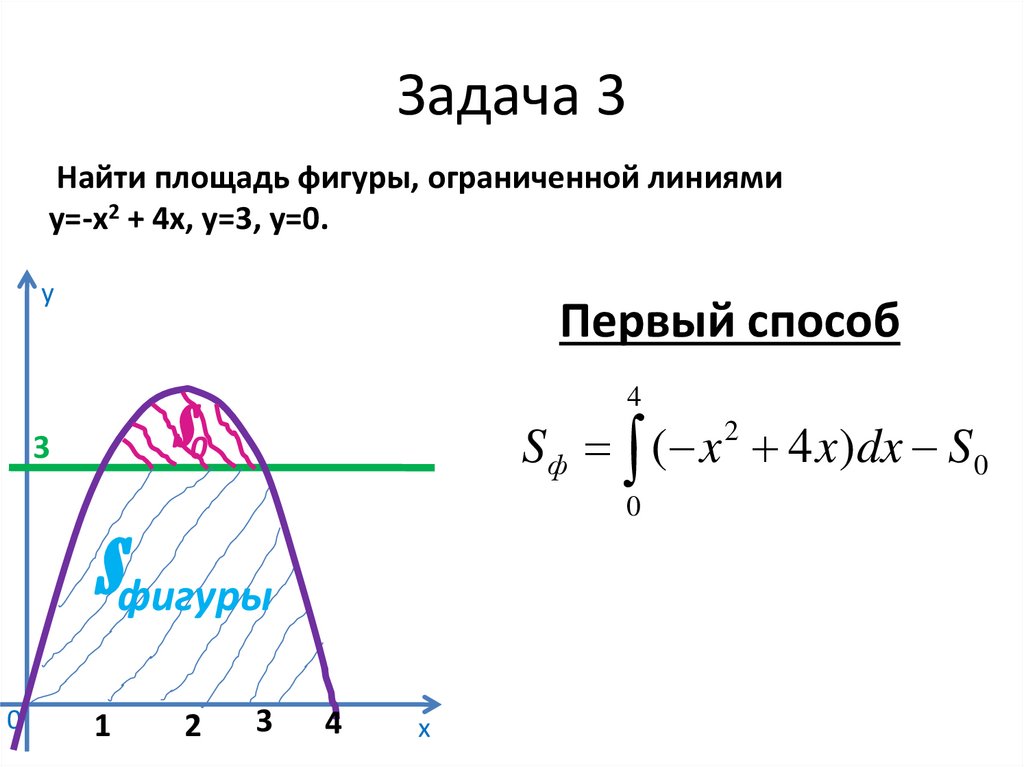
26. Задача 3

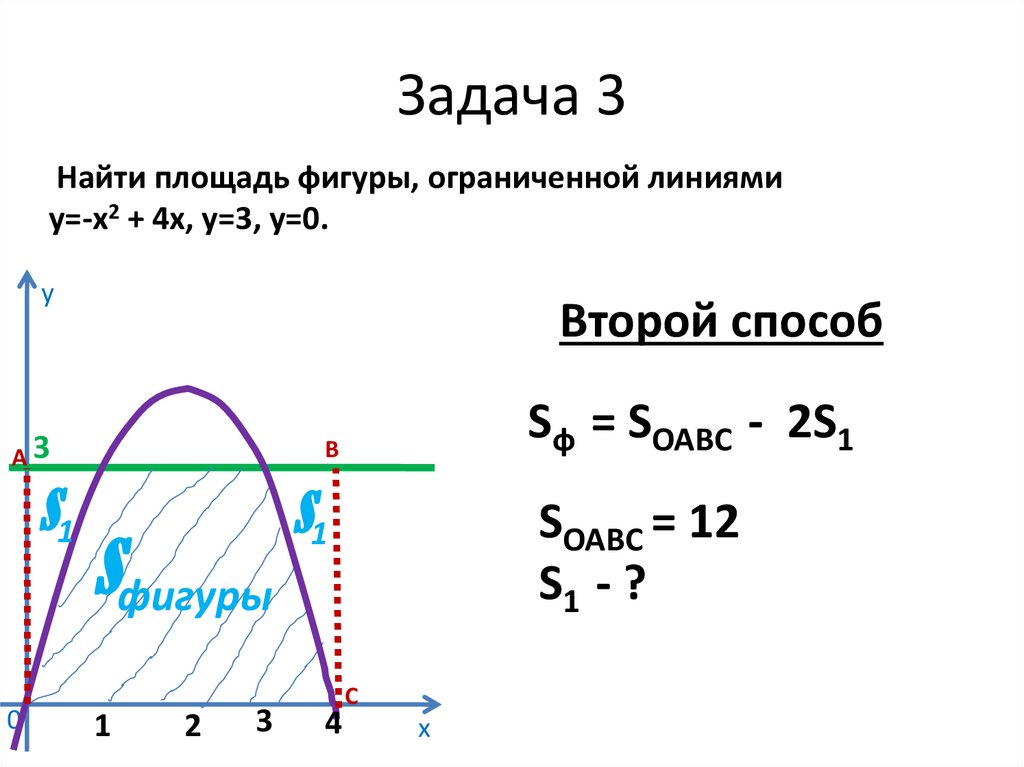
Найти площадь фигуры, ограниченной линиями
у=-х2 + 4х, у=3, у=0.
у
3
Sфигуры
0
1
2
3
4
х

27. Задача 3

Найти площадь фигуры, ограниченной линиями
у=-х2 + 4х, у=3, у=0.
у
Первый способ
4
S0
3
S ф ( x 4 x)dx S 0
2
0
Sфигуры
0
1
2
3
4
х

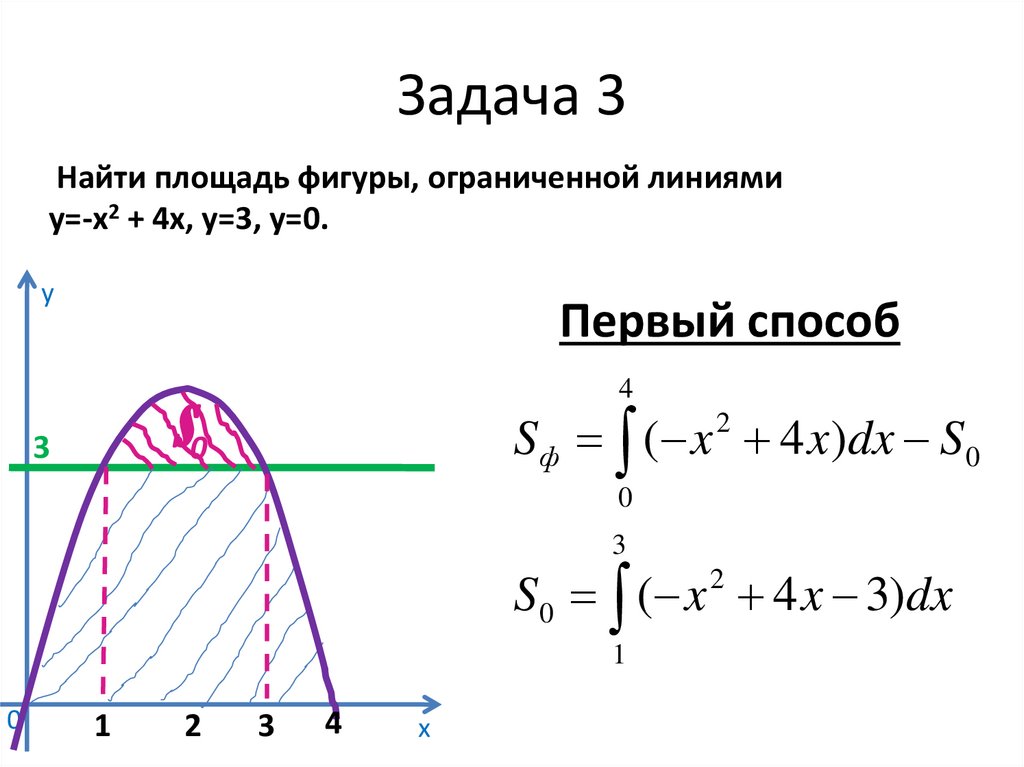
28. Задача 3

Найти площадь фигуры, ограниченной линиями
у=-х2 + 4х, у=3, у=0.
у
Первый способ
4
S0
3
S ф ( x 4 x)dx S 0
2
0
3
S 0 ( x 4 x 3)dx
2
1
0
1
2
3
4
х

29. Задача 3

4
3
4
x
2
2
2
0 ( x 4 x)dx ( 3 2 x ) 0 10 3
3
3
3
x
2
2
S 0 ( x 4 x 3)dx ( 2 x 3 x)
3
1
1
27
1
4
18 9 ( 2 3)
3
3
3
2 1
1
S ф 10 1 9
3 3
3

30. Задача 3

Найти площадь фигуры, ограниченной линиями
у=-х2 + 4х, у=3, у=0.
у
Второй способ
А3
S1
0
Sф = SОАВС - 2S1
В
Sфигуры
1
2
3
S1
4
SОАВС = 12
S1 - ?
С
х

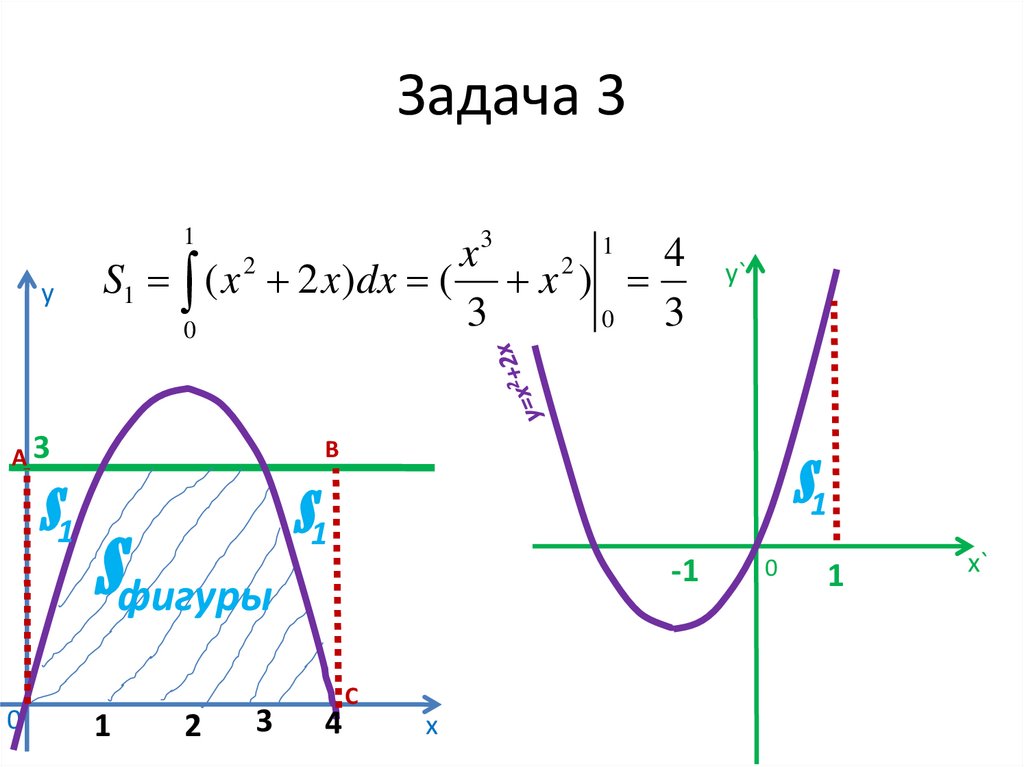
31. Задача 3

Найти площадь фигуры, ограниченной линиями
у=-х2 + 4х, у=3, у=0.
S1 - ?
у
А3
х`
0
S1
y`
В
Sфигуры
1
y`
2
3
S1
S1
-1
4
С
х
0
1
х`

32. Задача 3

1
у
3
1
x
4
2
2
S1 ( x 2 x)dx ( x )
3
3
0
0
А3
S1
0
y`
В
Sфигуры
1
2
3
S1
S1
-1
4
С
х
0
1
х`

33. Задача 3

Найти площадь фигуры, ограниченной линиями
у=-х2 + 4х, у=3, у=0.
у
А3
S1
0
Второй способ
Sф = SОАВС - 2S1
SОАВС = 12
В
Sфигуры
1
2
3
S1
4
4
S1
3
С
х
8
1
S ф 12 9
3
3

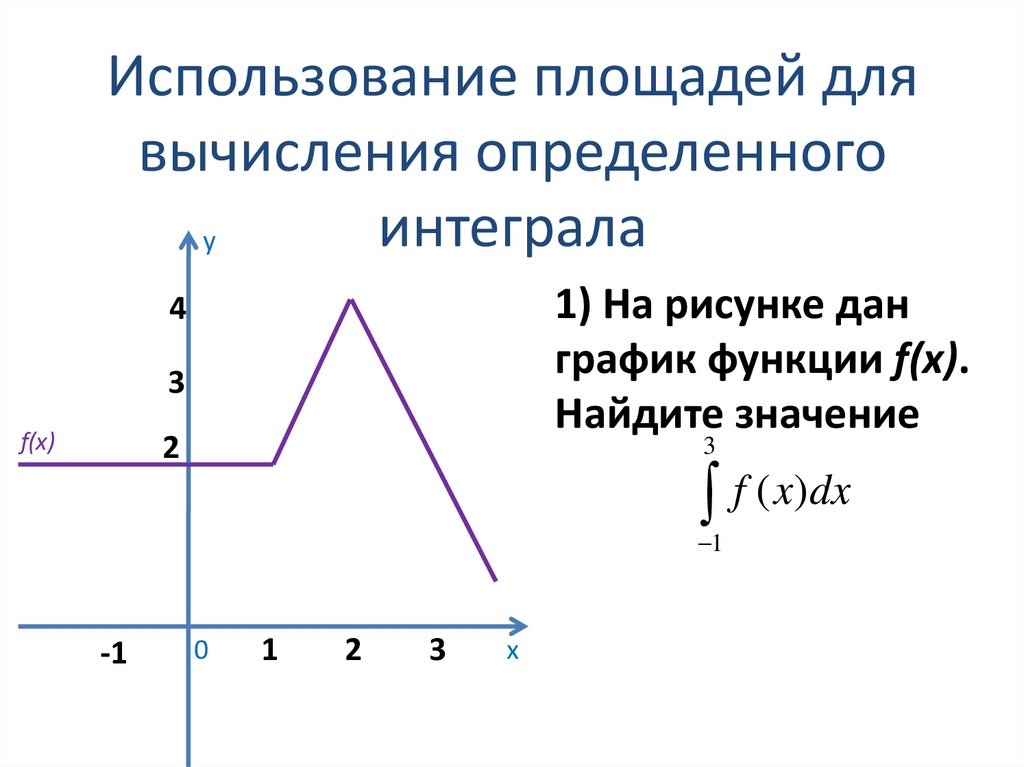
34. Использование площадей для вычисления определенного интеграла

у
1) На рисунке дан
график функции f(x).
Найдите значение
4
3
f(x)
2
3
f ( x)dx
1
-1
0
1
2
3
х

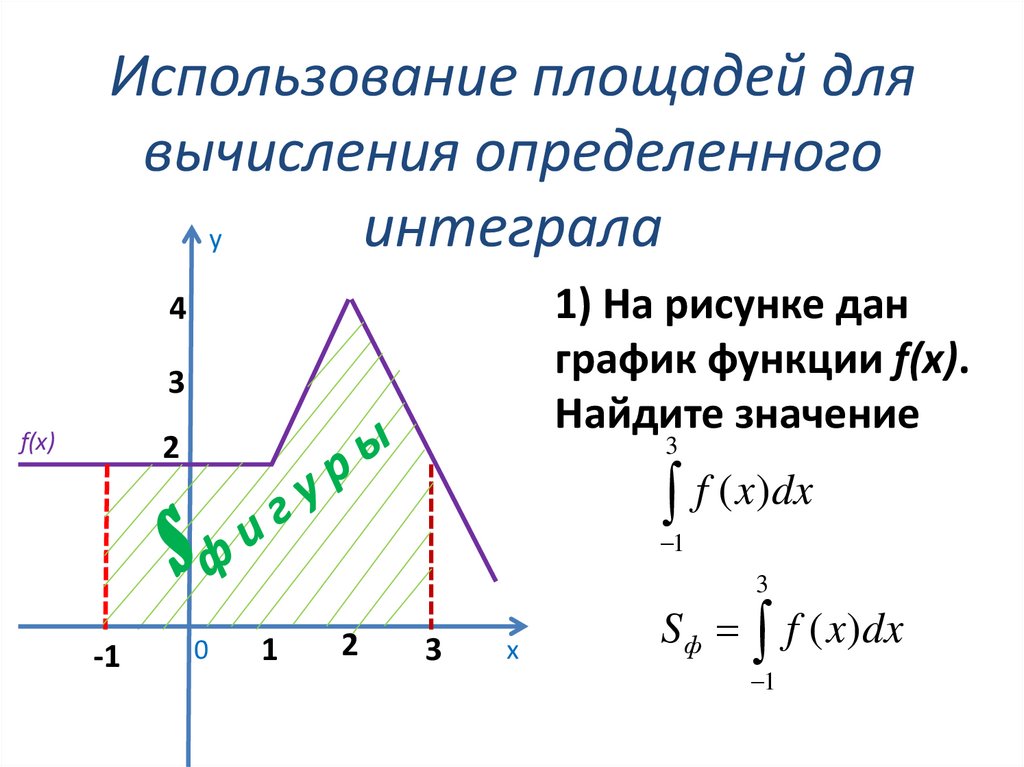
35. Использование площадей для вычисления определенного интеграла

у
1) На рисунке дан
график функции f(x).
Найдите значение
4
3
f(x)
2
3
f ( x)dx
1
3
-1
0
1
2
3
х
Sф
f ( x)dx
1

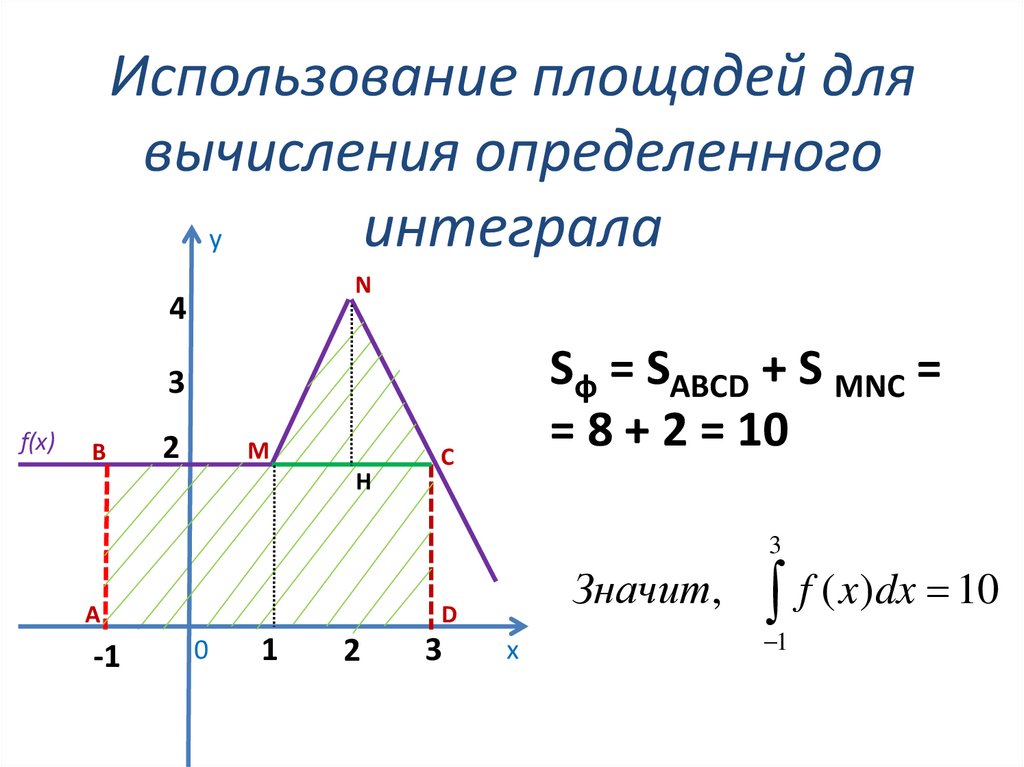
36. Использование площадей для вычисления определенного интеграла

у
N
4
Sф = SABCD + S MNC =
= 8 + 2 = 10
3
f(x)
В
2
M
H
С
3
А
-1
Значит,
D
0
1
2
3
х
f ( x)dx 10
1

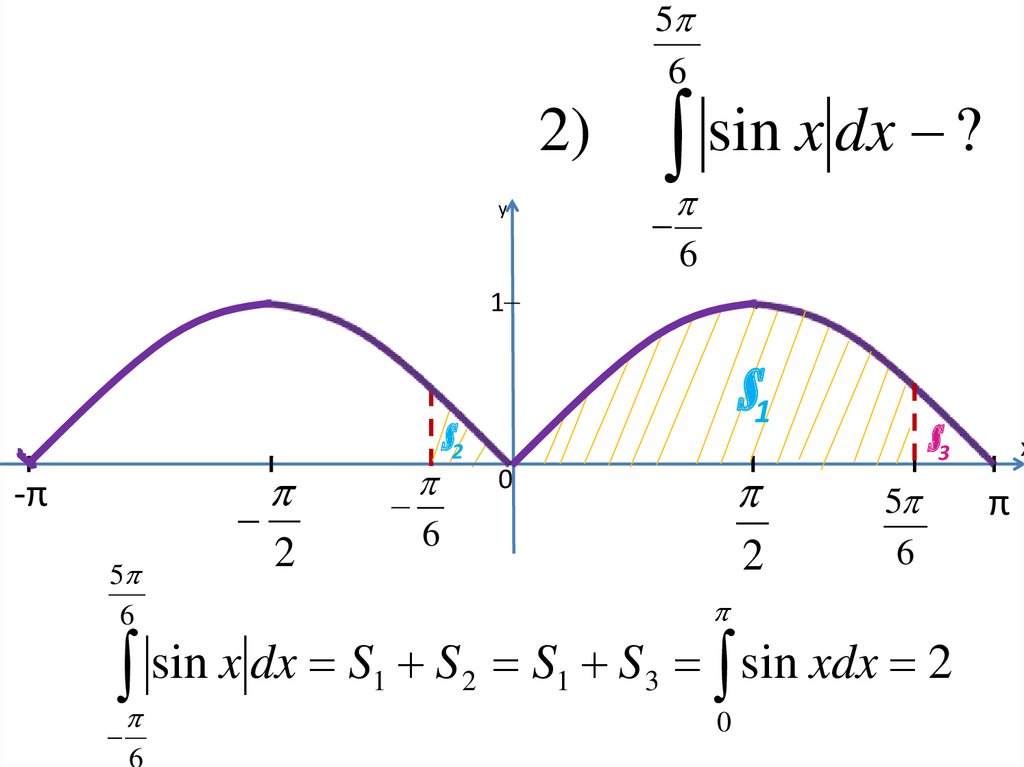
37.

5
6
2)
y
sin
x
dx
?
6
1
-π
5
6
2
sin x dx S
1
6
S1
S2
2
0
6
S3
5
6
S 2 S1 S3 sin xdx 2
0
x
π

38. Использование площадей для вычисления определенного интеграла

2
3)
Пусть
у 4 х
2
4 х 2 dx ?
2
Тогда у2 = 4 – х2, причем у ≥ 0.
Получаем: х2 + у2 = 4 – это окружность
с центром (0; 00) и радиусом 2. Но у ≥ 0!
Значит, берем только ту часть окружности,
которая выше оси Ох, т.е. полуокружность.
Нам нужно подсчитать площадь полукруга!

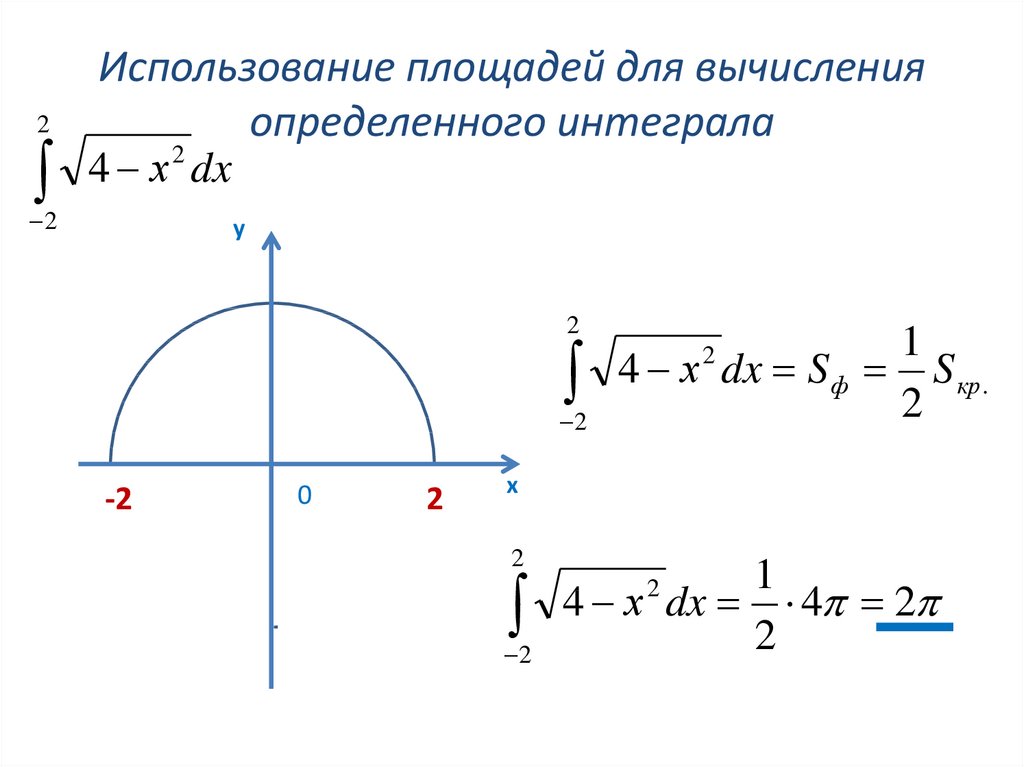
39. Использование площадей для вычисления определенного интеграла

2
Использование площадей для вычисления
определенного интеграла
4 х dx
2
2
у
2
2
-2
00
2
1
4 х dx S ф S кр .
2
2
х
2
2
1
4 х dx 4 2
2
2