Похожие презентации:
Решение задач на применение признаков подобия треугольников. 8 класс
1. Урок геометрии в 8 классе по теме: «Решение задач на применение признаков подобия треугольников»
Чему бы ты ни учился,ты учишься для себя.
(Петроний- сатирик Древней Греции)
2. Приветствую вас на уроке геометрии в 8 классе
3.
Интересныемысли и высказывания
Высшее назначение математики
- находить порядок в хаосе,
который нас окружает.
Н. Винер (1894 - 1964)
Успешного усвоения материала
4.
Экспресс-опрос потеории
5.
1. Отношением двух отрезковназывается … их длин
2. Отрезки АВ и CD называются
пропорциональными отрезкам
А1В1 и C1D1, если …
3. Прочитайте словами
равенство: АВ
ВС
АС
А1 В1 В1С1 А1С1
6.
3. Два треугольника называютсяподобными, если их углы …равны
и стороны одного треугольника
… сходственным сторонам …
4. Число k, равное отношению
сходственных сторон подобных
треугольников, называется … …
7.
5. Отношение площадей двухподобных треугольников
равно
… коэффициента подобия
6. Отношение периметров
подобных треугольников
равно … …
8.
7. Биссектриса треугольникаделит противоположную
сторону на отрезки,
пропорциональные … … …
(в учебнике №535)
8. Отношение сходственных
сторон подобных треугольников
равно отношению …, … … … …
(в учебнике № 543)
9.
9. Если два угла одноготреугольника … равны … …
другого, то такие треугольники …
10. Если две стороны одного
треугольника … двум сторонам
другого треугольника и углы, …
… этими сторонами, равны, то
такие треугольники …
10.
11. Если три стороны одноготреугольника … трем сторонам
другого треугольника, то такие
треугольники …
12. Если два треугольника
подобны, то их … стороны …,
а соответственные углы …
11.
13. Треугольники АВС и KDNподобны
1) Назовите
пропорциональные стороны.
2) Назовите равные углы.
12.
14. Все круги между собой …Коэффициент подобия равен
отношению … .
15. Все квадраты между собой …
Коэффициент подобия равен
отношению … .
16. Все равносторонние
треугольники между собой …
Коэффициент подобия равен
отношению … .
13.
17. Если сторона первогоквадрата в 2 раза меньше
стороны второго, то площадь
его … в … раз.
18. Если сторона одного
равностороннего треугольника
больше стороны другого в 4 раза,
то его площадь … в …раз.
19. Если радиус одного круга
больше радиуса другого в 5 раз,
то его площадь … в … раз.
14.
Решение задач на признакиподобия
пп.56-63
15. Цели урока:
-Закрепить теоретическиезнания по теме.
- Формировать навыки
применения признаков подобия
треугольников при решении
задач.
-Формировать правильную
математическую речь,
совершенствовать навыки
решения задач.
16.
Решаем задачи в группах(по рядам)
Проверка
17.
ПроверкаРешение:
ВС
5
2
АВ 10 2
;
;
В1С1 7,5 3
А1 В1 15 3
АС
7
2
Треугольники не
А1С1 9,5 3
являются подобными
18.
Решаем задачи в группах(по рядам)
Проверка
19.
ПроверкаРешение:
С 180 37 48 95
А1 180 95 48 37
А А1; В В1; С С1.
Треугольники являются подобными
по 1 признаку
20.
Решаем задачи в группах(по рядам)
Проверка
21.
ПроверкаРешение:
Так как С С1 90 , то по теореме
Пифагора:
АС АВ ВС 100 64 6
2
2
В1С1 А В А С 25 9 4
АС 6
ВС
8
2
2;
А1С1 3
В1С1 4
2
1 1
2
1 1
Треугольники являются подобными
по 2 признаку
22.
Решаем задачу в группахКМ=
Каждой группой решается вся задача
Отчёт
Группа 1-
а)
Группа 2-
б)
Проверка
Группа 3-
в)
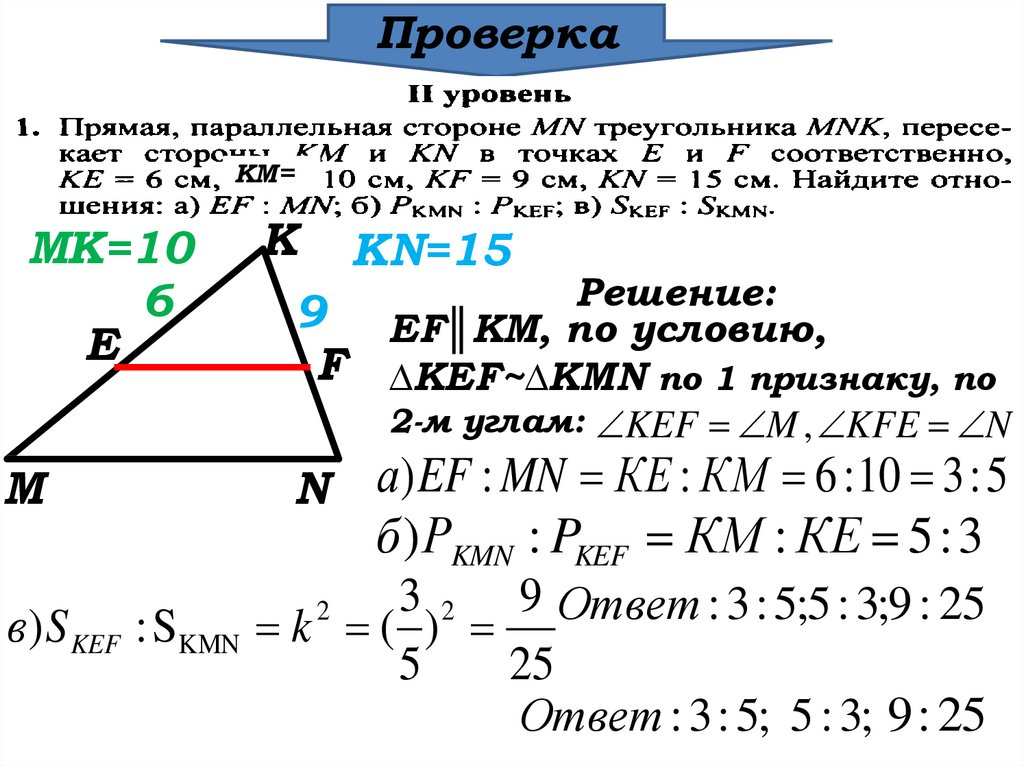
23.
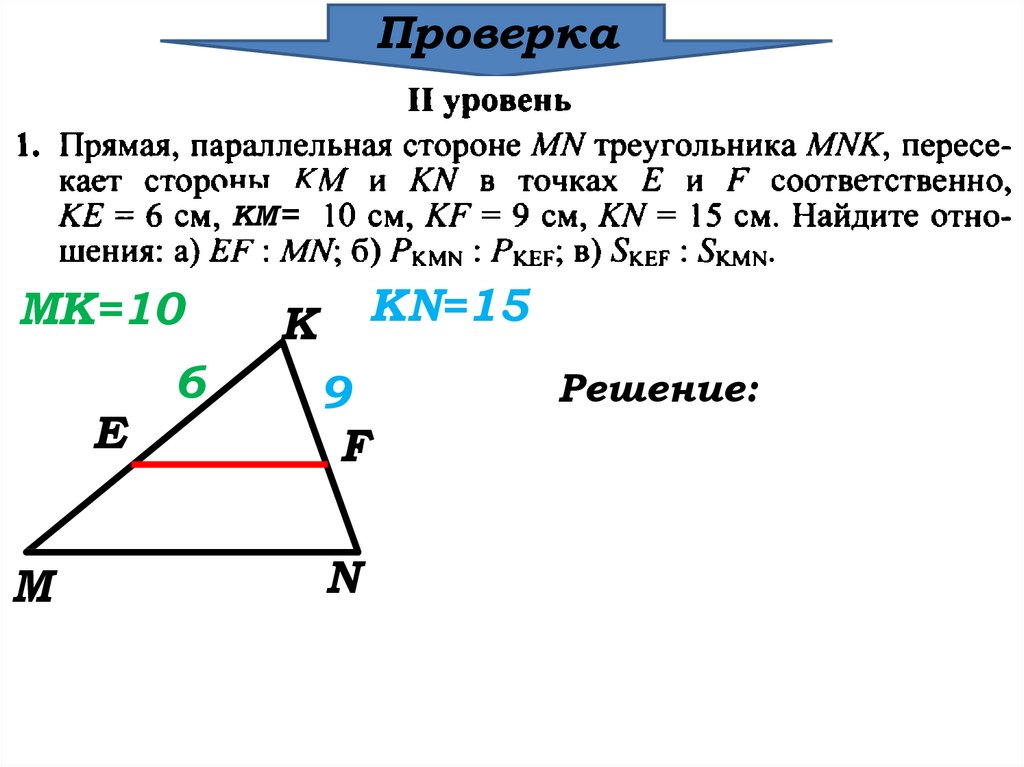
ПроверкаКМ=
MK=10
E
М
6
KN=15
К
9
F
N
Решение:
24.
ПроверкаКМ=
MK=10
E
М
6
К
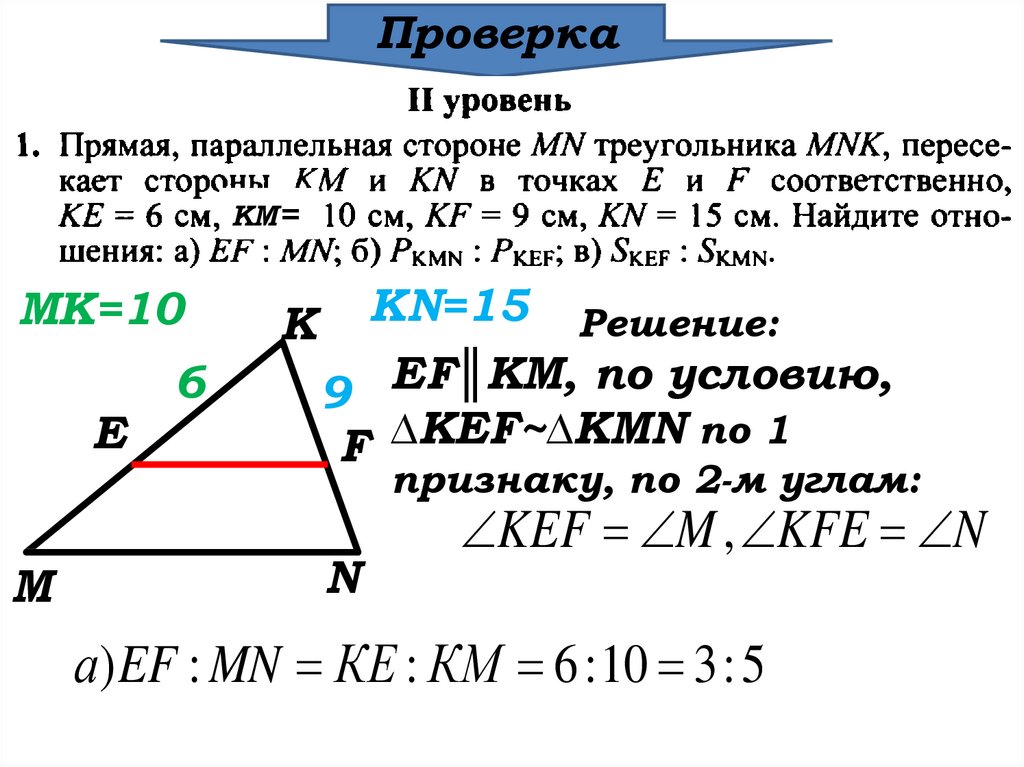
KN=15 Решение:
9 EF║KM, по условию,
∆KEF~∆KMN
по
1
F
признаку, по 2-м углам:
N
KEF M , KFE N
а) EF : MN КЕ : КМ 6 : 10 3 : 5
25.
ПроверкаКМ=
MK=10
E
М
6
К
KN=15
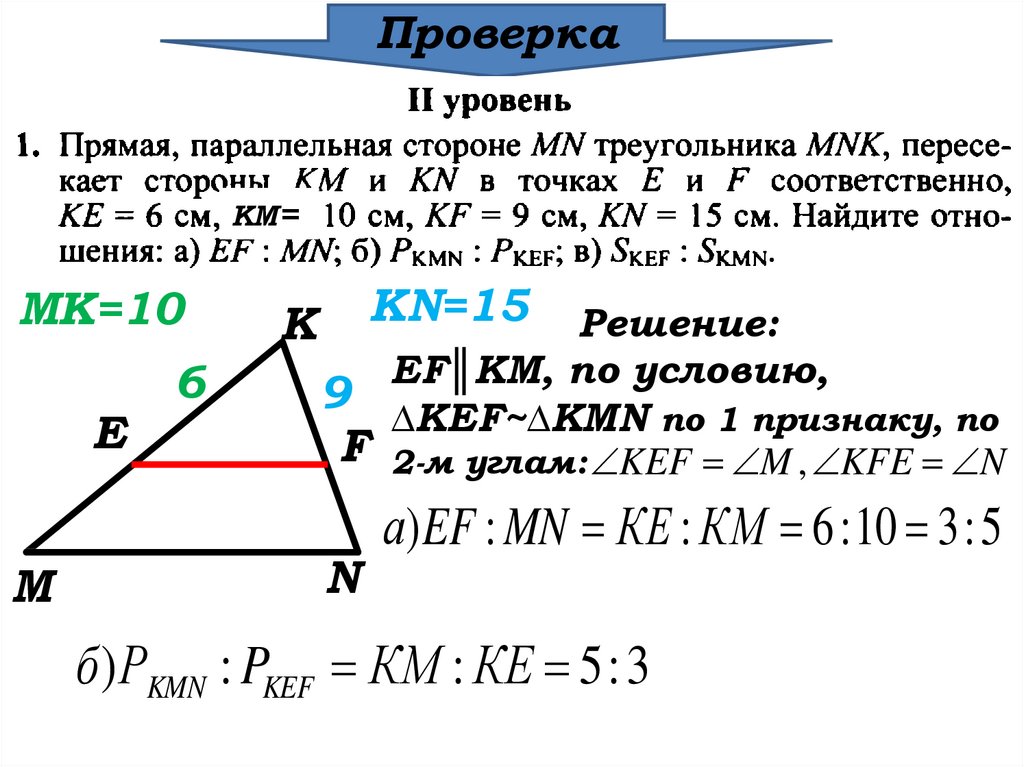
Решение:
EF║KM, по условию,
9
∆KEF~∆KMN по 1 признаку, по
F 2-м углам: KEF M , KFE N
N
а) EF : MN КЕ : КМ 6 : 10 3 : 5
б ) РKMN : PKEF КM : КE 5 : 3
26.
ПроверкаКМ=
MK=10
6
E
К
М
в ) S KEF : SKMN
KN=15
9
F
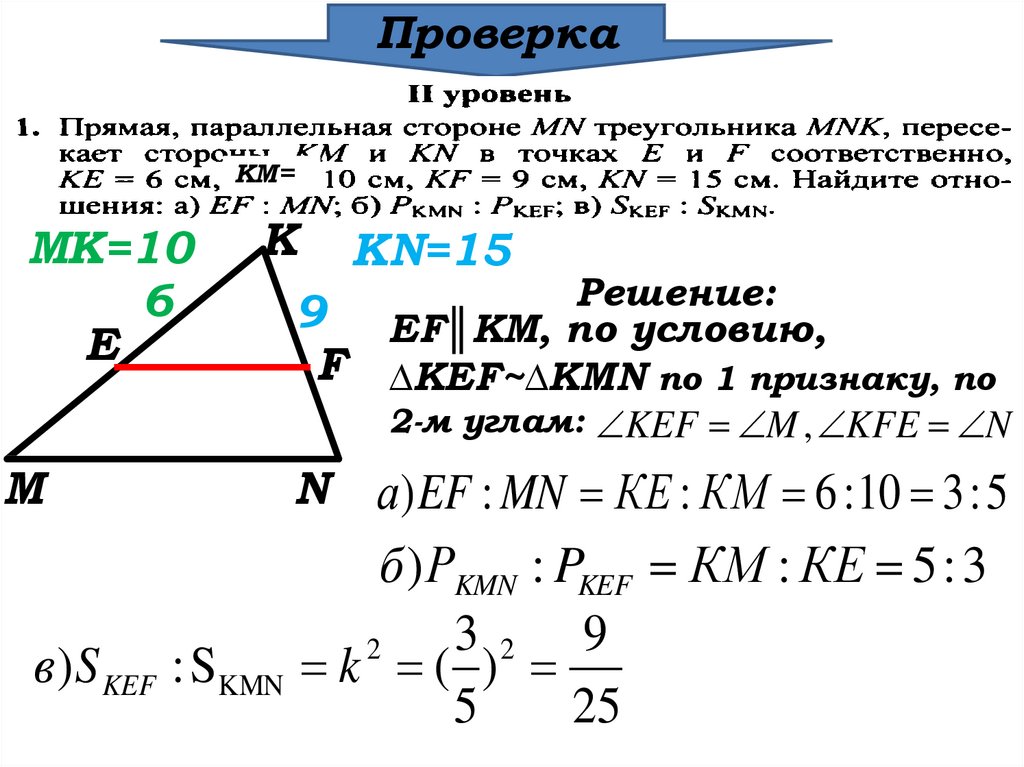
Решение:
EF║KM, по условию,
∆KEF~∆KMN по 1 признаку, по
2-м углам: KEF M , KFE N
а) EF : MN КЕ : КМ 6 : 10 3 : 5
б ) РKMN : PKEF КM : КE 5 : 3
3 2 9
2
k ( )
5
25
N
27.
ПроверкаКМ=
MK=10
6
E
М
в ) S KEF : SKMN
К
KN=15
9
F
N
Решение:
EF║KM, по условию,
∆KEF~∆KMN по 1 признаку, по
2-м углам: KEF M , KFE N
а) EF : MN КЕ : КМ 6 : 10 3 : 5
б ) РKMN : PKEF КM : КE 5 : 3
3 2 9 Ответ : 3 : 5;5 : 3;9 : 25
k ( )
5
25
Ответ : 3 : 5; 5 : 3; 9 : 25
2
28.
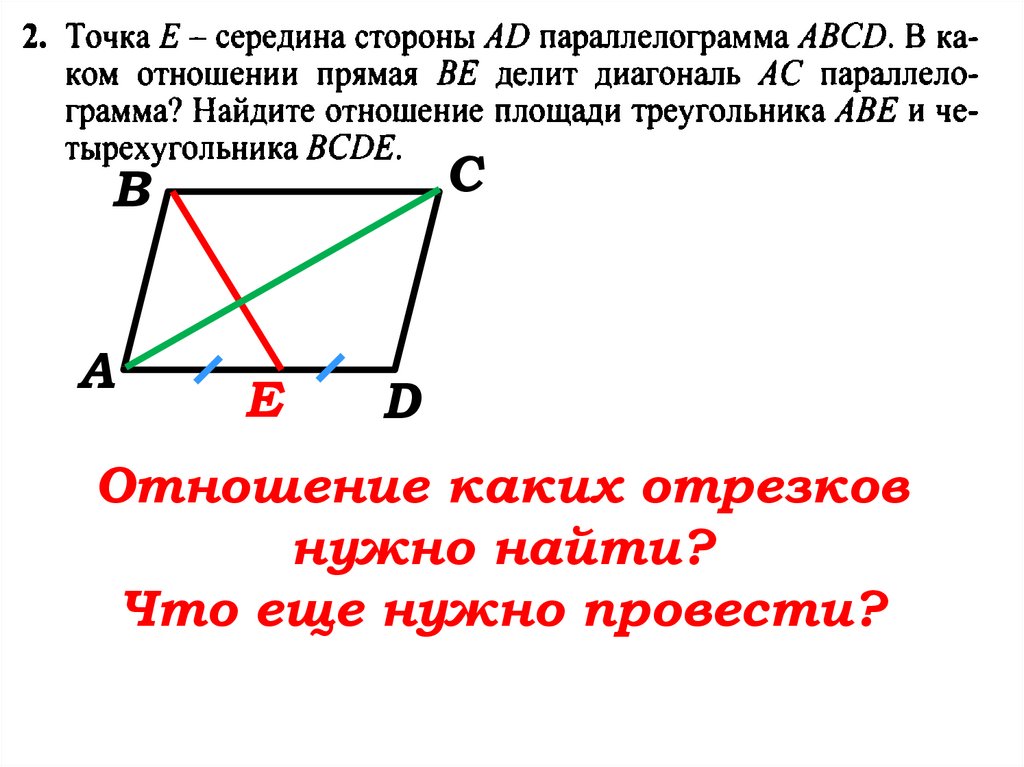
Решаем задачу вместеКакая фигура дана?
Что нужно провести?
29.
СВ
А
E
D
Отношение каких отрезков
нужно найти?
Что еще нужно провести?
30.
KВ
М
Р
А
С
E
D
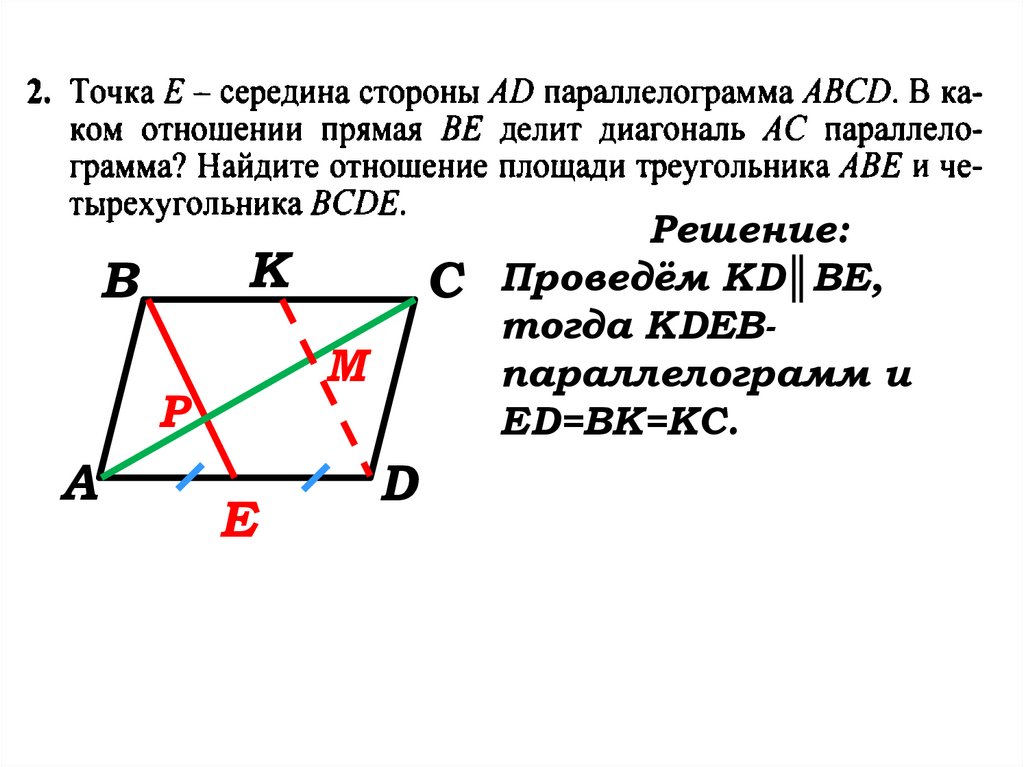
Решение:
Проведём KD║BE,
тогда
31.
KВ
М
Р
А
С
E
D
Решение:
Проведём KD║BE,
тогда КDEBпараллелограмм и
ED=BK=KC.
32.
KВ
М
Р
А
С
E
D
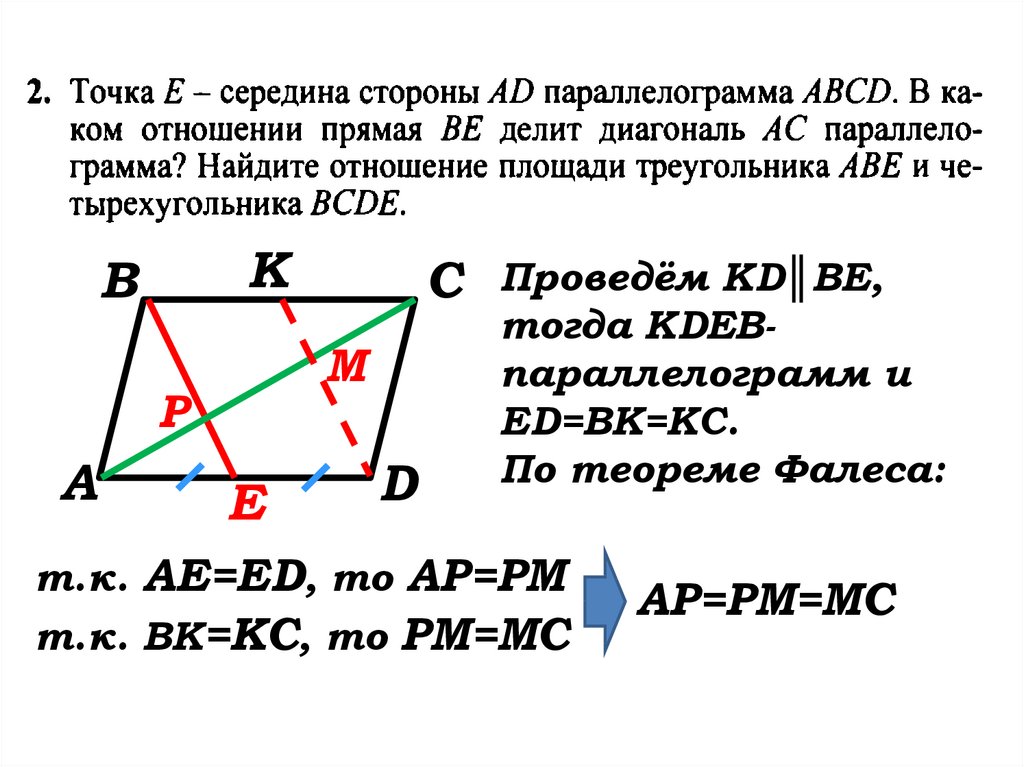
Решение:
Проведём KD║BE,
тогда ВКDEпараллелограмм и
АЕ=ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
33.
KВ
М
Р
А
С
E
D
Решение:
Проведём KD║BE,
тогда КDEBпараллелограмм и
ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
т.к. ВК=КС, то РМ=МС
34.
KВ
М
Р
А
С
E
D
Проведём KD║BE,
тогда КDEBпараллелограмм и
ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
т.к. ВК=КС, то РМ=МС
АР=РМ=МС
35.
KВ
М
Р
А
С
E
D
Проведём KD║BE,
тогда КDEBпараллелограмм и
ED=BK=KC.
По теореме Фалеса:
т.к. АЕ=ED, то АР=РМ
т.к. ВК=КС, то РМ=МС
АР:РС=1:2
АР=РМ=МС
36.
KВ
Проведём диагональ BD
М
Р
А
С
E
D
Назовите
равновеликие
треугольники
37.
KВ
М
Р
А
С
E
D
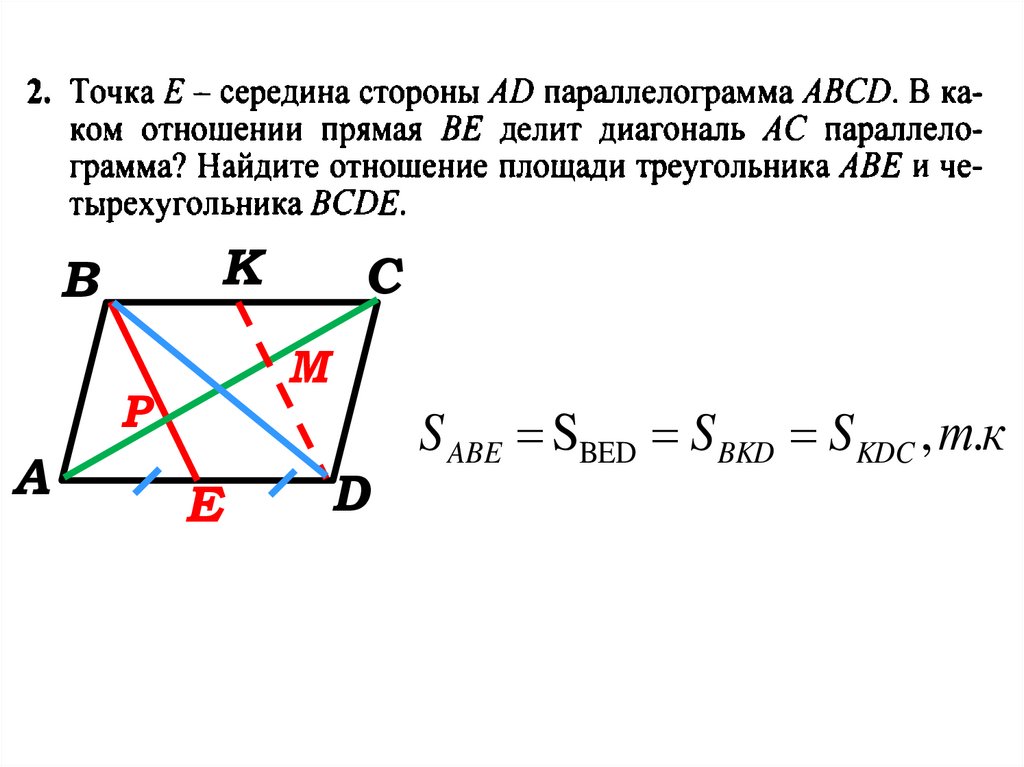
S ABE SBED S BKD S KDC , т.к
38.
KВ
М
Р
А
С
E
D
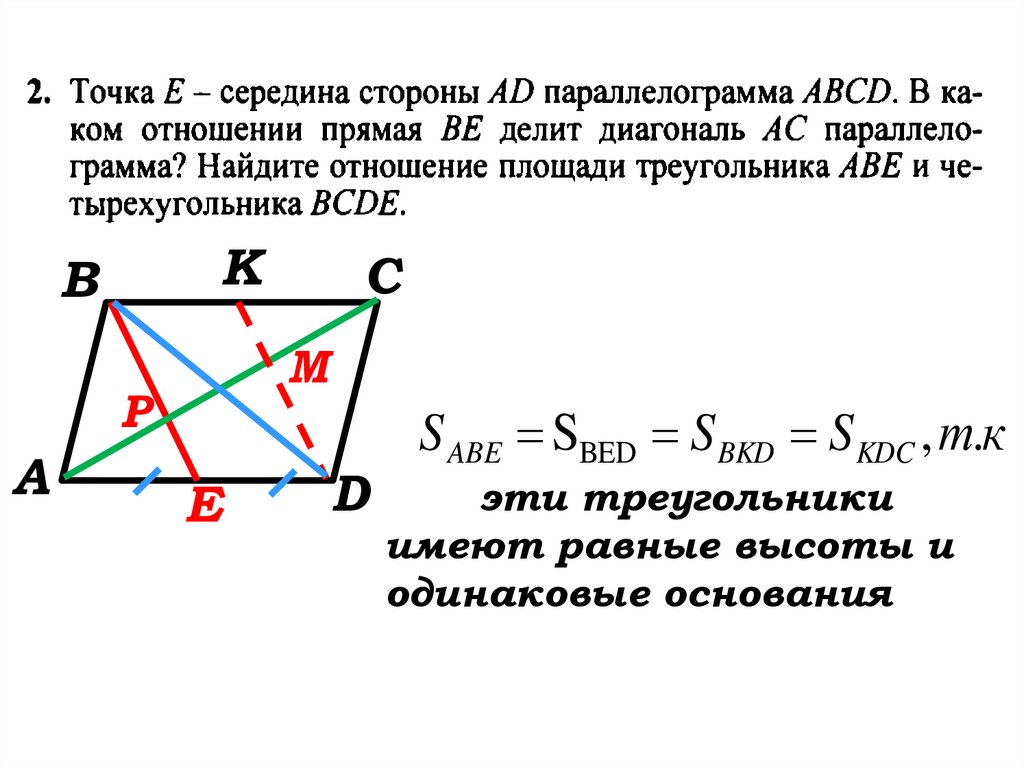
S ABE SBED S BKD S KDC , т.к
эти треугольники
имеют равные высоты и
одинаковые основания
39.
KВ
М
Р
А
С
E
D
S ABE SBED S BKD S KDC , т.к
эти треугольники имеют равные
высоты и одинаковые основания
S ABE : SBCDE 1 : 3
Ответ : 1 : 2; 1 : 3
40.
Решаем задачу вместеПрочитайте задачу, выполните
чертеж без обозначений
41.
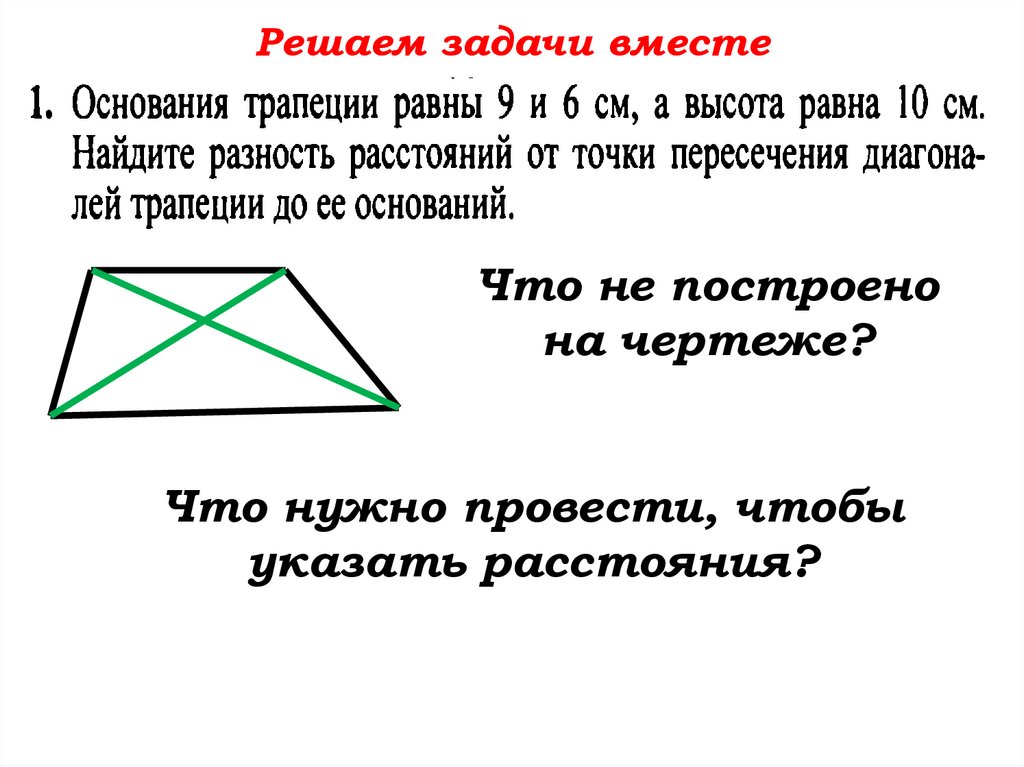
Решаем задачи вместеЧто не построено
на чертеже?
Что нужно провести, чтобы
указать расстояния?
42.
Решаем задачи вместеЗапишите краткое условие
43.
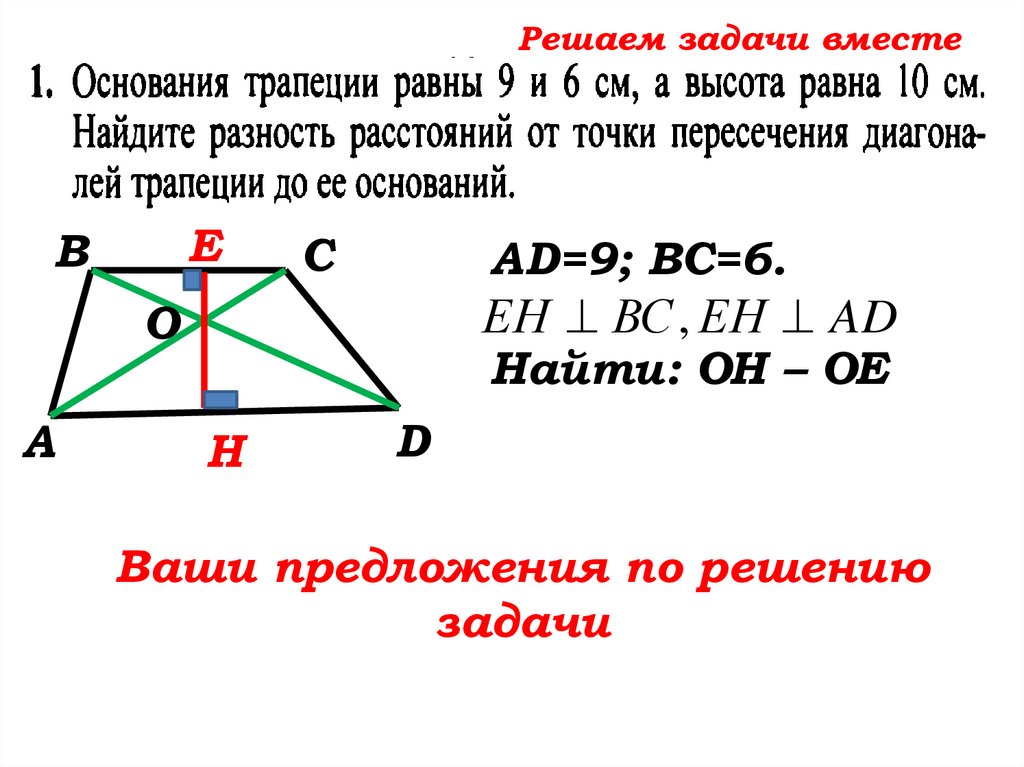
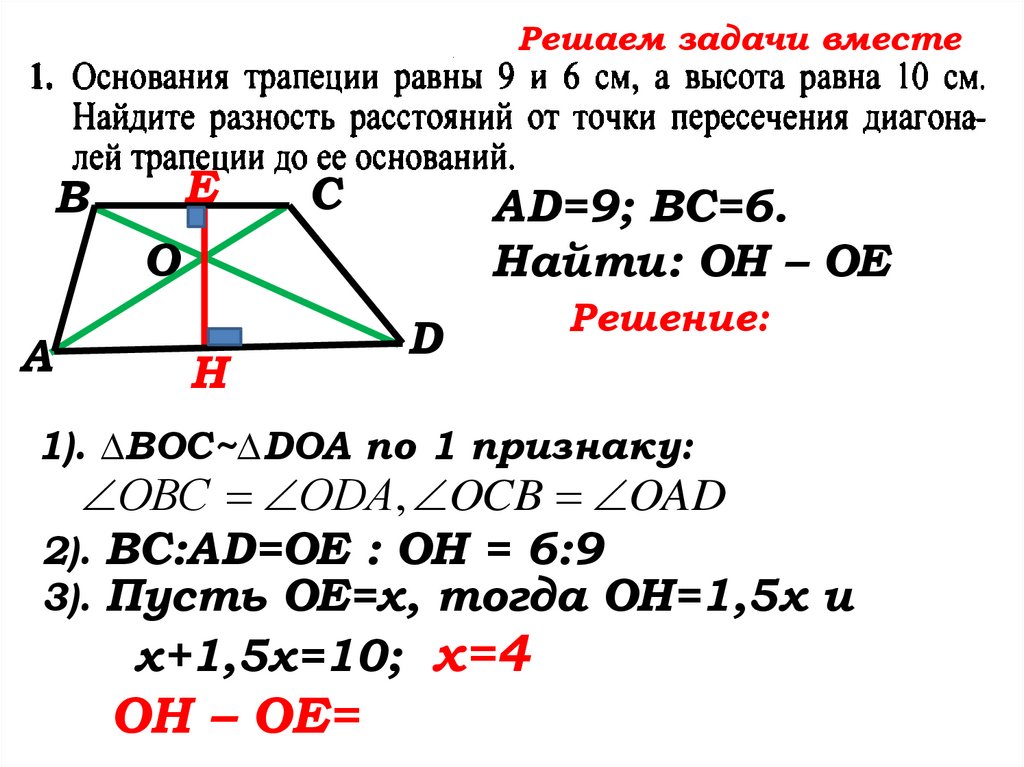
Решаем задачи вместеЕ
В
С
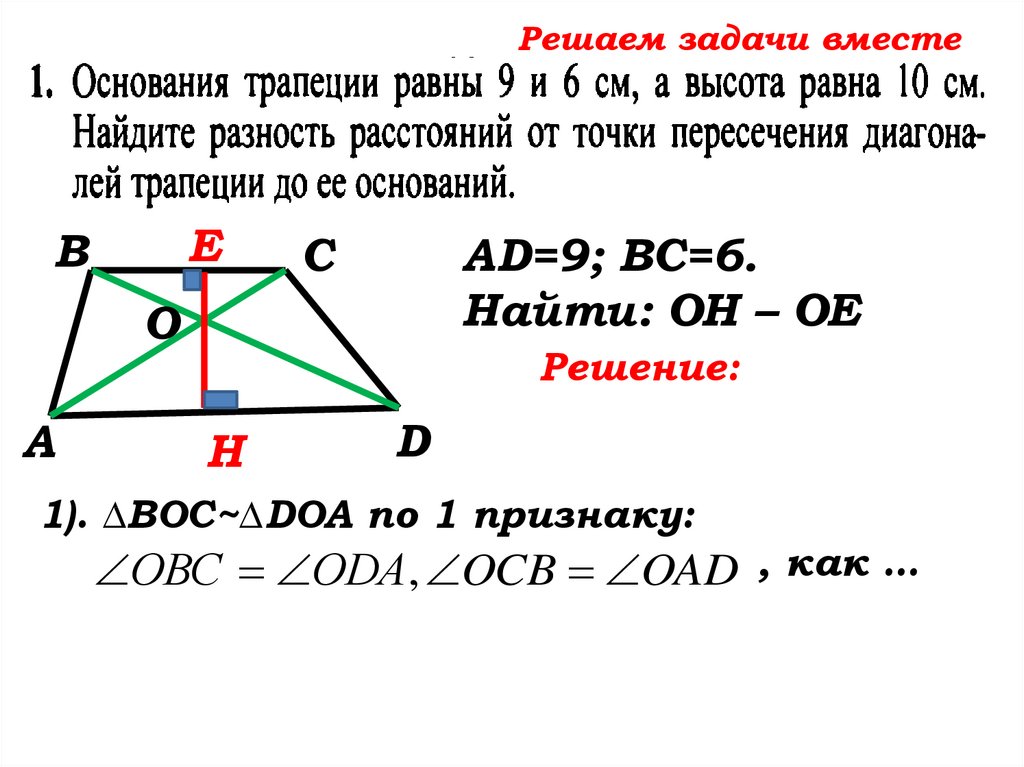
AD=9; ВС=6.
ЕН ВС , ЕН AD
О
А
Найти: ОН – ОЕ
Н
D
Ваши предложения по решению
задачи
44.
Решаем задачи вместеЕ
В
AD=9; ВС=6.
ЕН ВС , ЕН AD
Найти: ОН – ОЕ
С
О
А
Н
D
1). ∆ВОС~∆… по …
Решение:
45.
Решаем задачи вместеЕ
В
AD=9; ВС=6.
Найти: ОН – ОЕ
С
О
А
Решение:
Н
D
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD , как …
46.
Решаем задачи вместеЕ
В
AD=9; ВС=6.
Найти: ОН – ОЕ
С
О
А
Решение:
Н
D
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD , как
накрест лежащие при пересечении
параллельных прямых ВС и AD секущими
BD и АС
47.
Решаем задачи вместеЕ
В
AD=9; ВС=6.
Найти: ОН – ОЕ
С
О
А
Решение:
Н
D
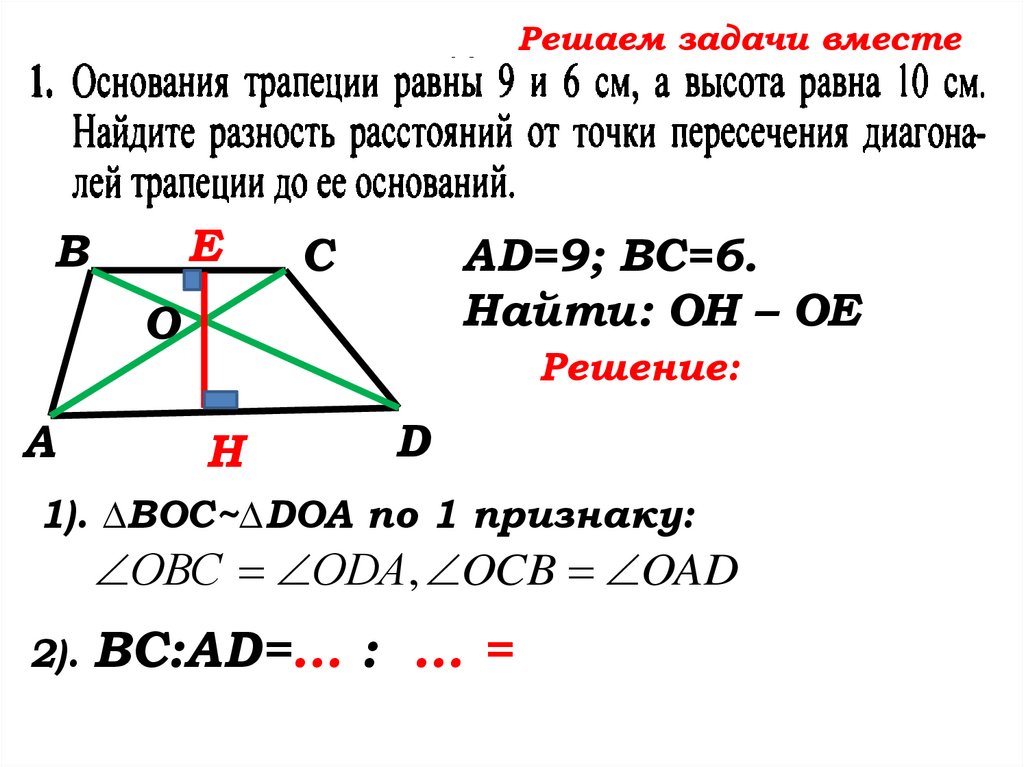
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2).
ВС:AD=… : … =
48.
Решаем задачи вместеЕ
В
AD=9; ВС=6.
Найти: ОН – ОЕ
С
О
А
Решение:
Н
D
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2).
ВС:AD=ОЕ : ОН= 6:9
49.
Решаем задачи вместеЕ
В
AD=9; ВС=6.
Найти: ОН – ОЕ
С
О
А
Решение:
Н
D
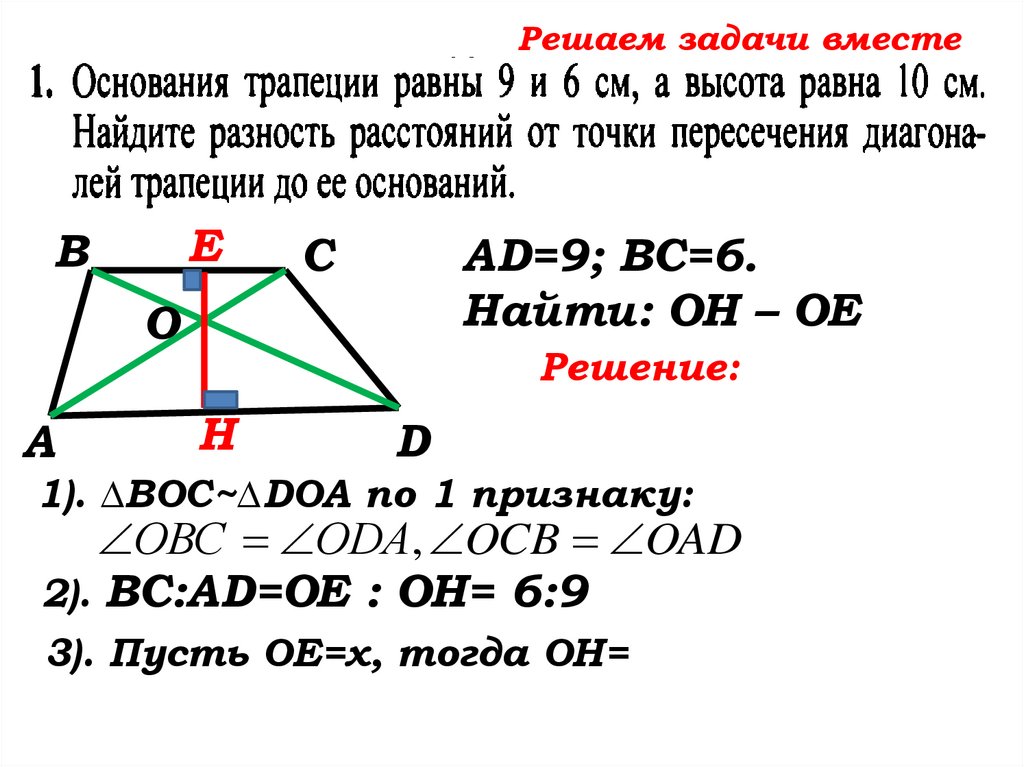
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2). ВС:AD=ОЕ : ОН= 6:9
3). Пусть ОЕ=х, тогда ОН=
50.
Решаем задачи вместеЕ
В
AD=9; ВС=6.
Найти: ОН – ОЕ
С
О
А
Решение:
Н
D
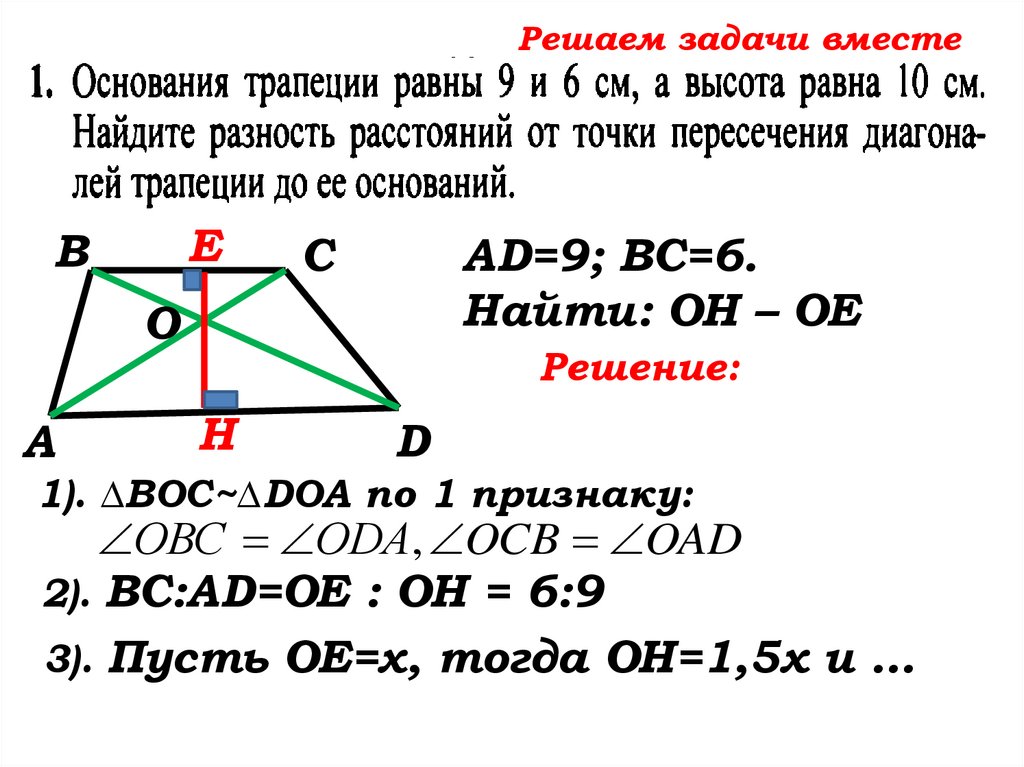
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и …
51.
Решаем задачи вместеЕ
В
С
AD=9; ВС=6.
Найти: ОН – ОЕ
О
А
Н
D
Решение:
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10
52.
Решаем задачи вместеЕ
В
С
AD=9; ВС=6.
Найти: ОН – ОЕ
О
А
Н
D
Решение:
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10; х=4
53.
Решаем задачи вместеЕ
В
С
AD=9; ВС=6.
Найти: ОН – ОЕ
О
А
Н
D
Решение:
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10; х=4
ОН – ОЕ=
54.
Решаем задачи вместеЕ
В
С
AD=9; ВС=6.
Найти: ОН – ОЕ
О
А
Н
D
Решение:
1). ∆ВОС~∆DOA по 1 признаку:
ОВС ОDA, OCB OAD
2). ВС:AD=ОЕ : ОН = 6:9
3). Пусть ОЕ=х, тогда ОН=1,5х и
х+1,5х=10; х=4
ОН – ОЕ= 6 – 4 = 2(см)
Ответ: 2см.
55.
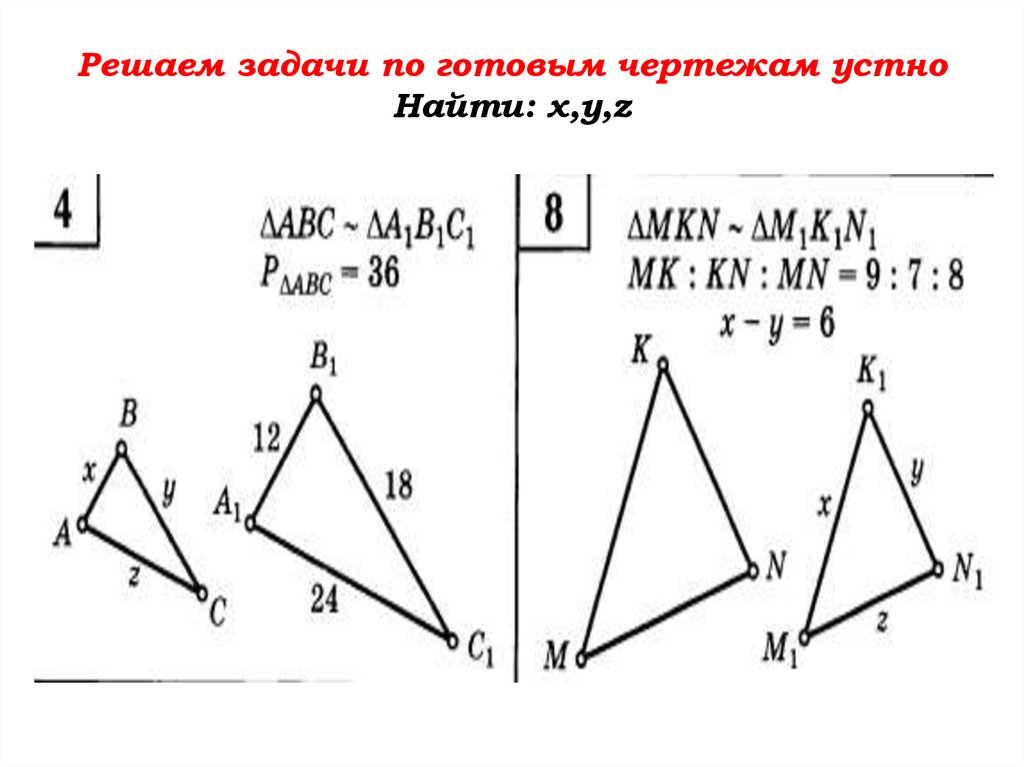
Решаем задачи по готовым чертежам устноНайти: х,у,z
56.
Решаем задачи по готовым чертежам.Найти: х,у,z
57.
Решаем задачи по готовым чертежам устноНайти: х,у,z
58.
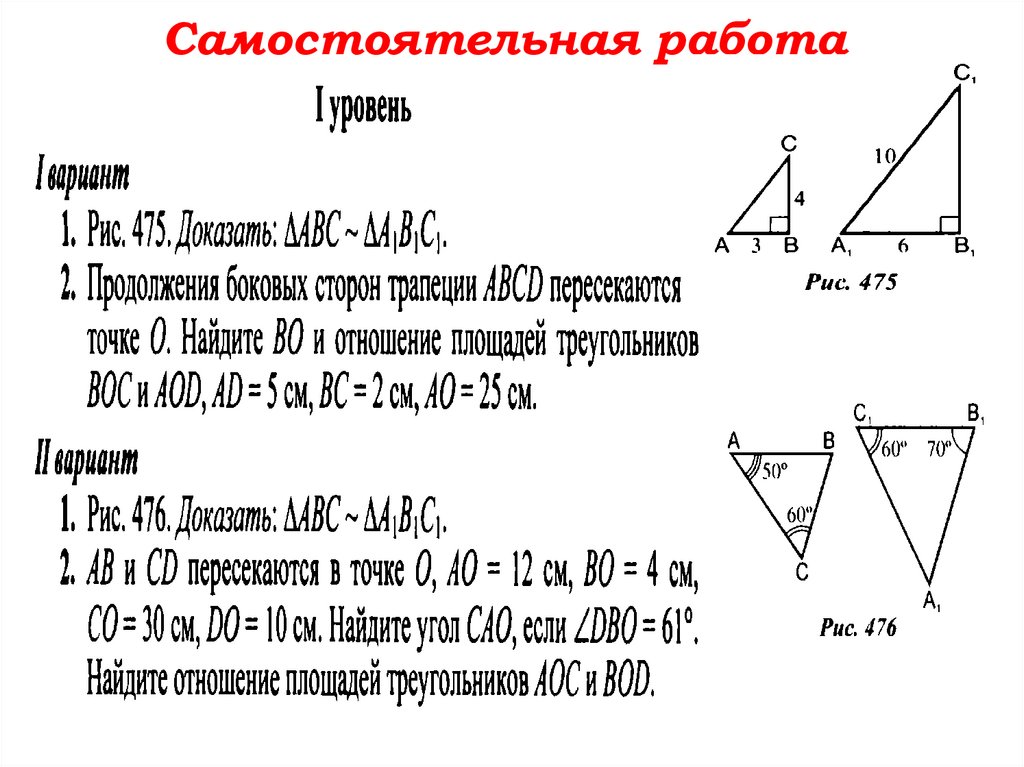
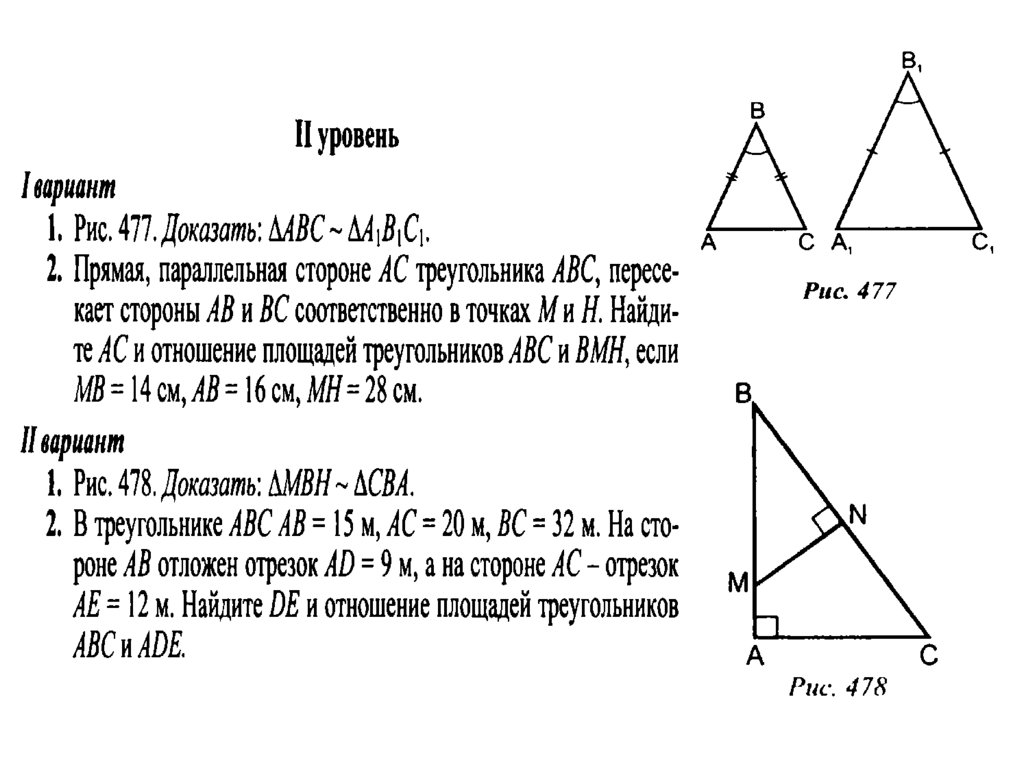
Самостоятельная работа59.
60.
АВ
61.
Поставьте себе оценку за урокКритерии оценки за урок:
1. Комментировали ДЗ
2. Активно участвовали в
решении устных задач.
3. Привели решение задач,
решаемых письменно
62.
Назовите ученика, которыйпо вашему мнению был сегодня
на уроке лучшим
63.
Домашнее заданиеТеория: Повторить опр. подобных
треугольников, выводы из задач, формулировку
3-х признаков подобия треугольников
Практика: разобрать классные задачи.
1. Прорешать задачи самостоятельной
работы следующего уровня на отдельном
листе.
Дополнительная задача
64.
Рекомендации к дополнительной задачеОбозначить:
1) коэффициент пропорциональности за
k,
2) катет одного треугольника за
гипотенузу за
с;
а,
а другого
соответственно за а1 и с1.
По теореме Пифагора найти другой
катет каждого треугольника и
показать, что стороны треугольников
пропорциональны.











































 Математика
Математика








