Похожие презентации:
Параллелепипед
1. ПАРАЛЛЕЛЕПИПЕД
2.
Параллелепи́пед (от греч. παράλλος параллельный и греч.επιπεδον плоскость) призма, основанием которой служит
параллелограмм, или (равносильно) многогранник, у которого
шесть граней и каждая из них параллелограмм.
Как понять и запомнить слово параллелепипед?
Разобъем его на две составляющие:
параллеле - означает параллельный (греч.),
пипед - означает плоскость (греч.).
Или геометрическое тело, ограниченное параллельными плоскостями.
Для понимания, что же это за
геометрическое тело, наилучшим образом
подходит обыкновенный кирпич.
Это самый настоящий прямоугольный
параллепипед.
3.
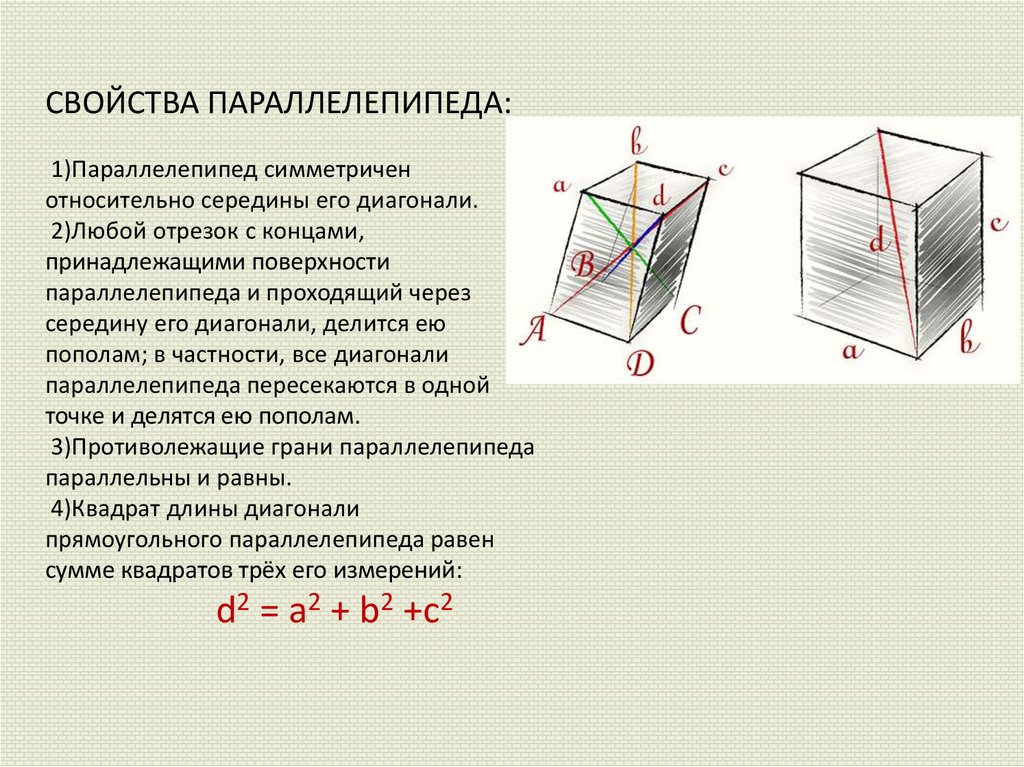
СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА:1)Параллелепипед симметричен
относительно середины его диагонали.
2)Любой отрезок с концами,
принадлежащими поверхности
параллелепипеда и проходящий через
середину его диагонали, делится ею
пополам; в частности, все диагонали
параллелепипеда пересекаются в одной
точке и делятся ею пополам.
3)Противолежащие грани параллелепипеда
параллельны и равны.
4)Квадрат длины диагонали
прямоугольного параллелепипеда равен
сумме квадратов трёх его измерений:
d2 = a2 + b2 +c2
4.
Площадь поверхности прямоугольногопараллелепипеда равна удвоенной сумме площадей
трех граней этого параллелепипеда:
S= 2(Sa+Sb+Sc)= 2(ab+ bc+ ac)
Объем прямоугольного
параллелепипеда равен произведению
площади основания на высоту:
V= SH= abc
5.
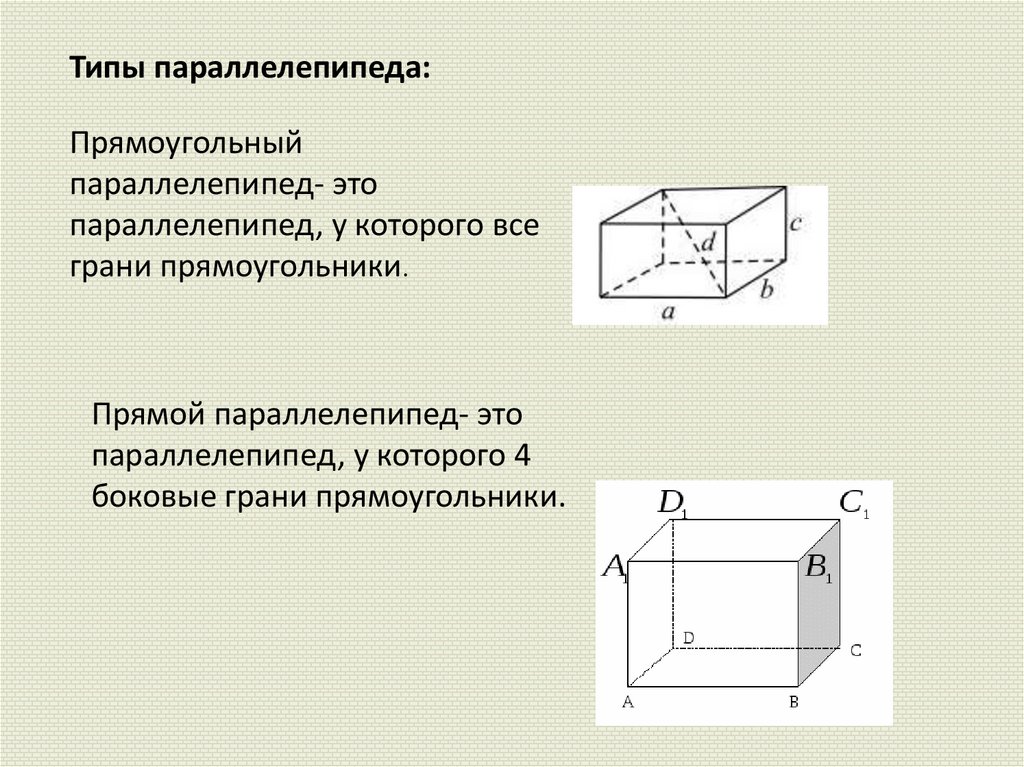
Типы параллелепипеда:Прямоугольный
параллелепипед- это
параллелепипед, у которого все
грани прямоугольники.
Прямой параллелепипед- это
параллелепипед, у которого 4
боковые грани прямоугольники.
6.
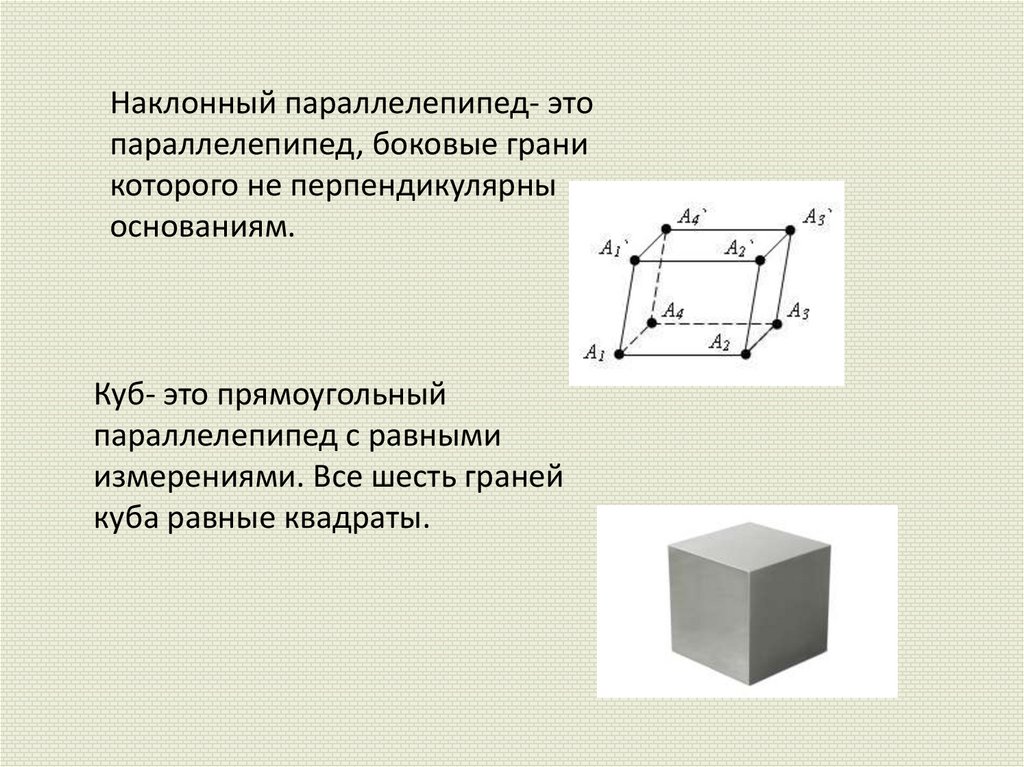
Наклонный параллелепипед- этопараллелепипед, боковые грани
которого не перпендикулярны
основаниям.
Куб- это прямоугольный
параллелепипед с равными
измерениями. Все шесть граней
куба равные квадраты.
7.
Основные элементы параллелепипеда:1) Две грани параллелепипеда, не имеющие общего
ребра, называются противоположными, а имеющие
общее ребро смежными.
2) Две вершины параллелепипеда, не принадлежащие
одной грани, называются противоположными.
3) Отрезок, соединяющий противоположные вершины,
называется диагональю параллелепипеда.
4) Длины трёх рёбер прямоугольного параллелепипеда,
имеющих общую вершину, называют его измерениями.





 Математика
Математика








