Похожие презентации:
Скалярное произведение векторов. Вычисление углов между прямыми
1.
Скалярное произведениевекторов.
Вычисление углов между
прямыми.
2.
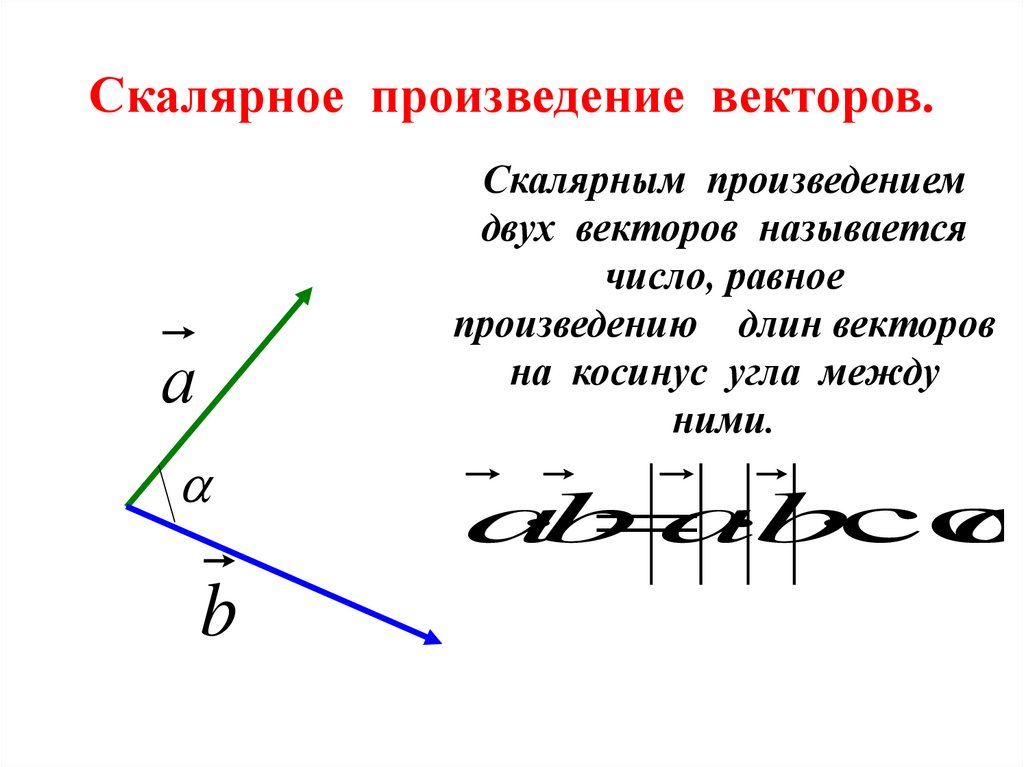
Скалярное произведение векторов.Скалярным произведением
двух векторов называется
число, равное
произведению длин векторов
на косинус угла между
ними.
а
b
a
b
a
b
cos
3.
ab a b cos
Если
Если
Если
a b = 0
a b 0
, то
a b
- острый угол
a b 0 , то - тупой угол
, то
4.
Формула скалярного произведениявекторов в пространстве.
а x1;y1;z1
b x2;y2;z2
a
b
x
x
y
y
z
z
12
12
12
Скалярное произведение двух векторов равно
сумме произведений соответствующих
координат этих векторов.
5.
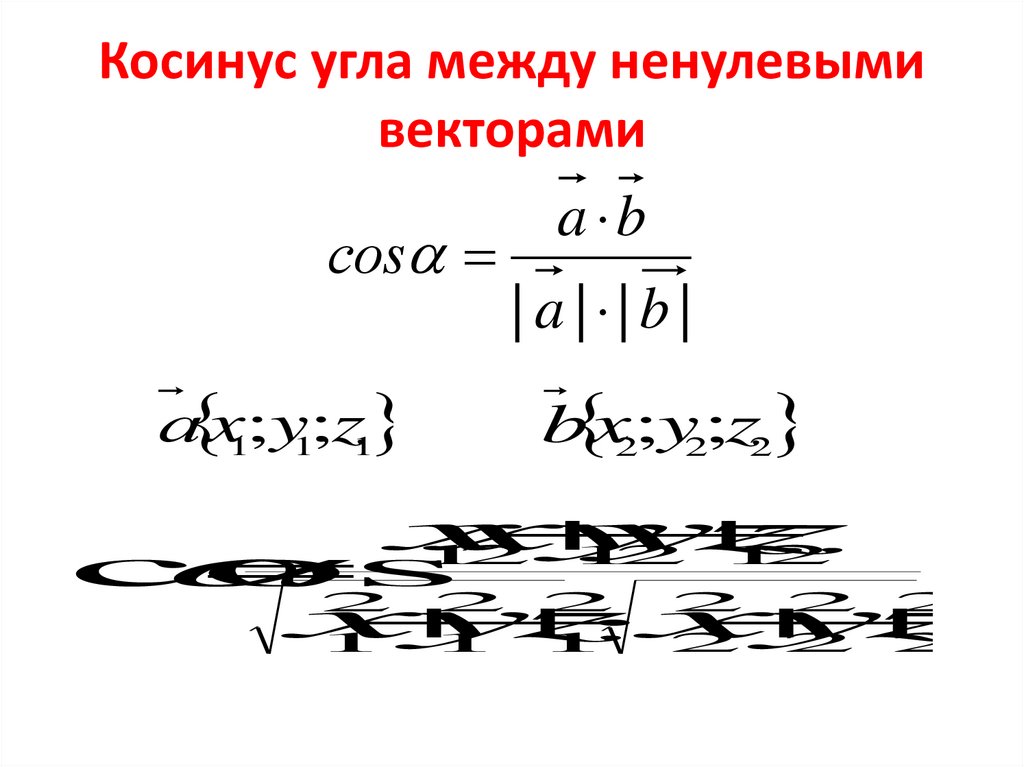
Косинус угла между ненулевымивекторами
соs
а x1;y1;z1
a b
| a | |b |
b x2;y2;z2
x
x
y
y
z
z
1
2 1
2 1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1 1 1
2 2 2
6.
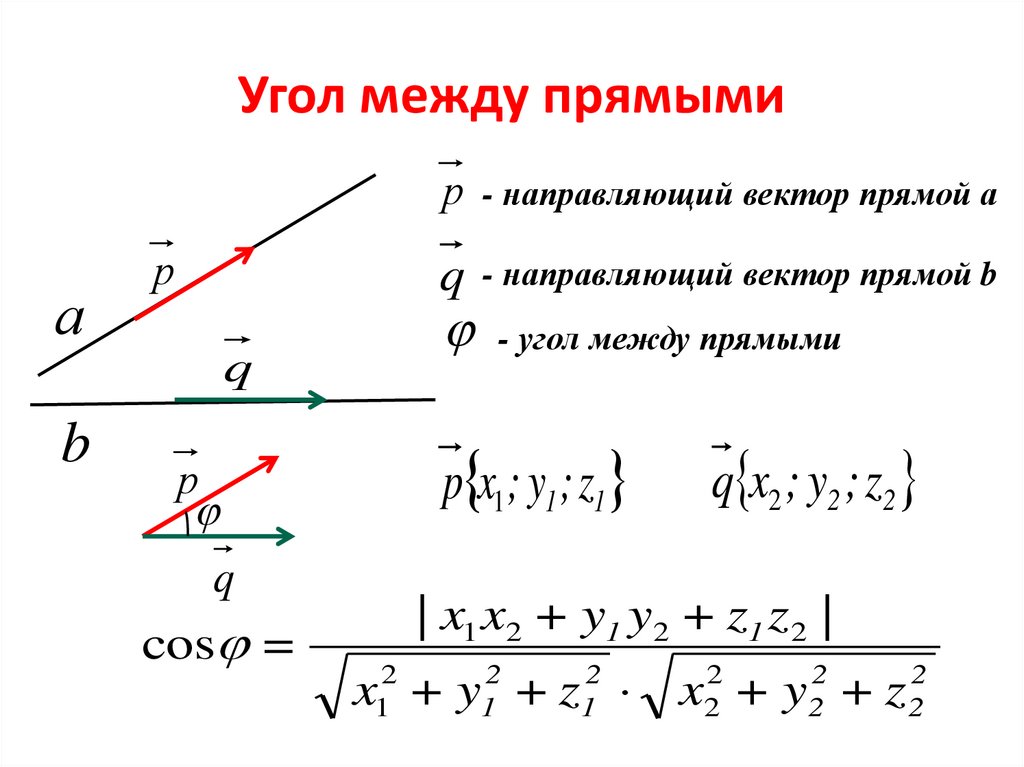
Угол между прямымиа
р
q
b
р
q
cos =
р
- направляющий вектор прямой а
q
- направляющий вектор прямой b
- угол между прямыми
p x1 ; y1 ; z1
q x2 ; y2 ; z2
| x1 x2 + y1 y2 + z1 z 2 |
x12 + y12 + z12 x22 + y22 + z 22
7.
8.
9.
10.
11.
12.
Решение задач:№ 464(б)
Вычислить угол между прямыми AB и CD, если
A(5;-8;-1), В(6;-8;-2), С(7;-5;-11), D(7;-7;-9)
Решение
AB 1;0; 1
cos =
СD 0; 2;2
| 1 0 0 ( 2) ( 1) 2 |
12 0 2 ( 1) 2 0 2 ( 2) 2 2 2
1
cos
2
60
0
13.
№ 464(в)Вычислить угол между прямыми AB и CD, если
A(1;0;2), В(2;1;0), С(0;-2;-4), D(-2;-4;0)
Решение
AB 1;1; 2
СD 2; 2;4
Так как координаты векторов пропорциональны,
то векторы коллинеарны, а прямые параллельны.
0
0
14.
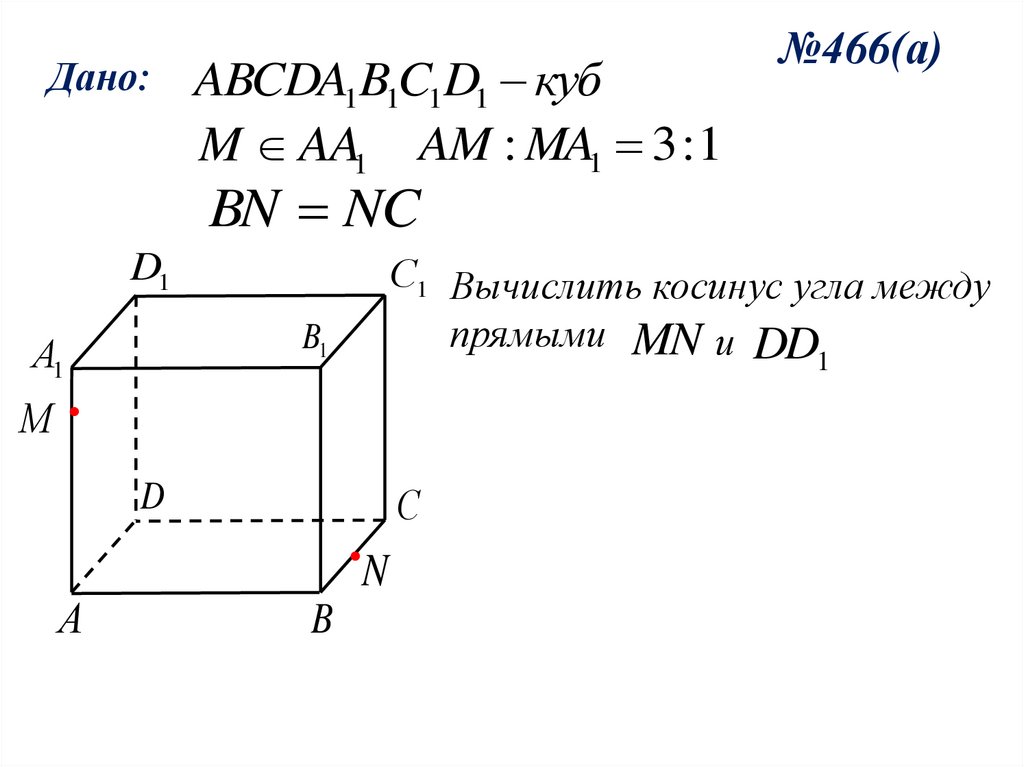
Дано:ABCDA1B1C1D1 куб
M AA1 AM : MA1 3 :1
№466(а)
BN NC
С1 Вычислить косинус угла между
прямыми MN и DD
D1
B1
А1
1
М
С
D
А
N
B
15.
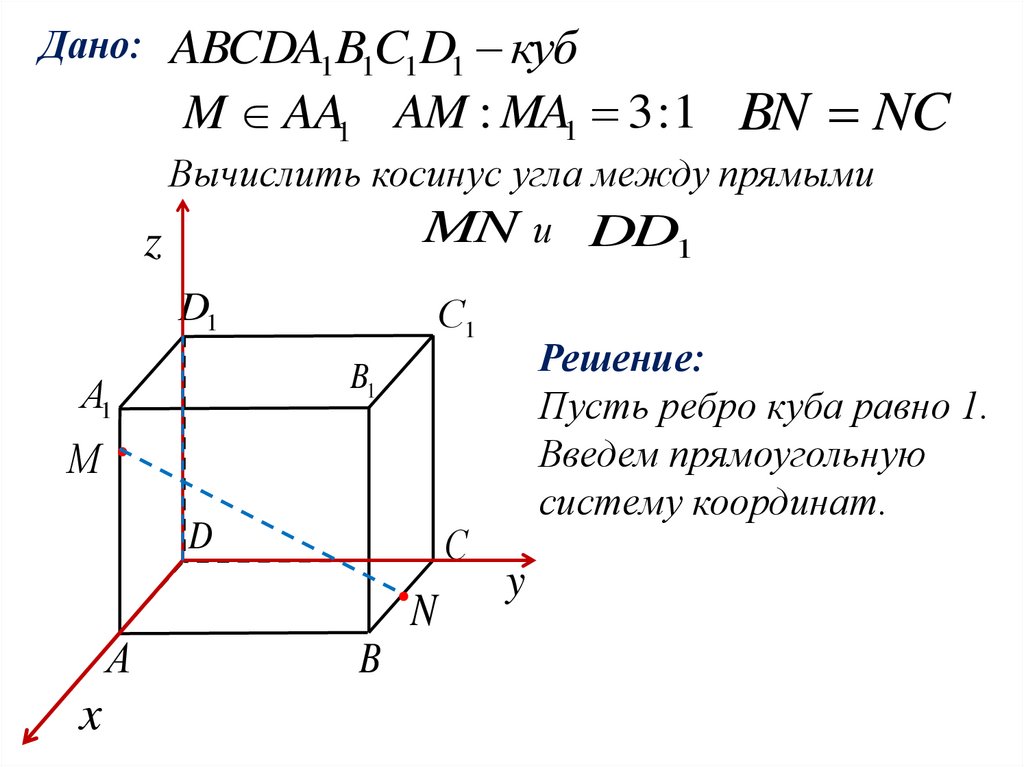
Дано:ABCDA1B1C1D1 куб
M AA1 AM : MA1 3 :1 BN NC
Вычислить косинус угла между прямыми
MN и DD1
z
С1
D1
Решение:
Пусть ребро куба равно 1.
Введем прямоугольную
систему координат.
B1
А1
М
С
D
А
x
N
B
y
16.
zС1
D1
B1
А1
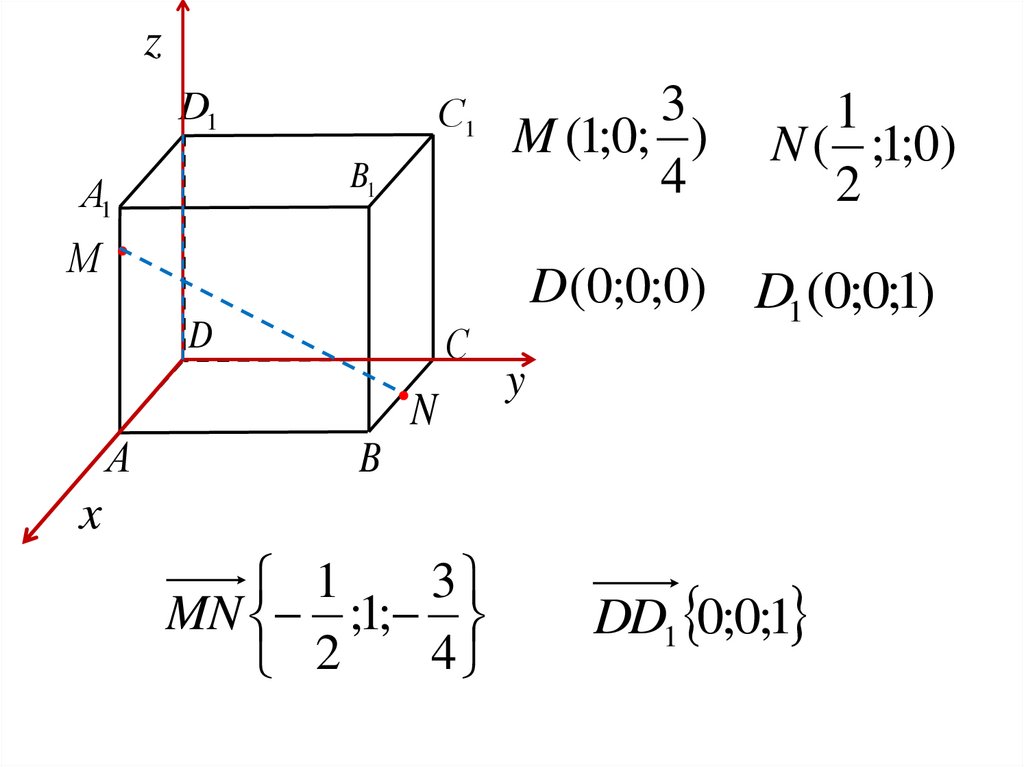
3
M (1;0; )
4
М
С
D
А
N
1
N ( ;1;0)
2
D(0;0;0) D1 (0;0;1)
y
B
x
3
1
MN ;1;
4
2
DD1 0;0;1
17.
31
MN ;1;
4
2
cos =
DD1 0;0;1
1
3
| 0 1 0 ( ) 1 |
2
4
2
2
1
3
2
2
2
2
1 0 0 1
2
4
3
cos
29
18.
Домашнее заданиеП.46-50
№ 466 (б,в), № 468 (б)

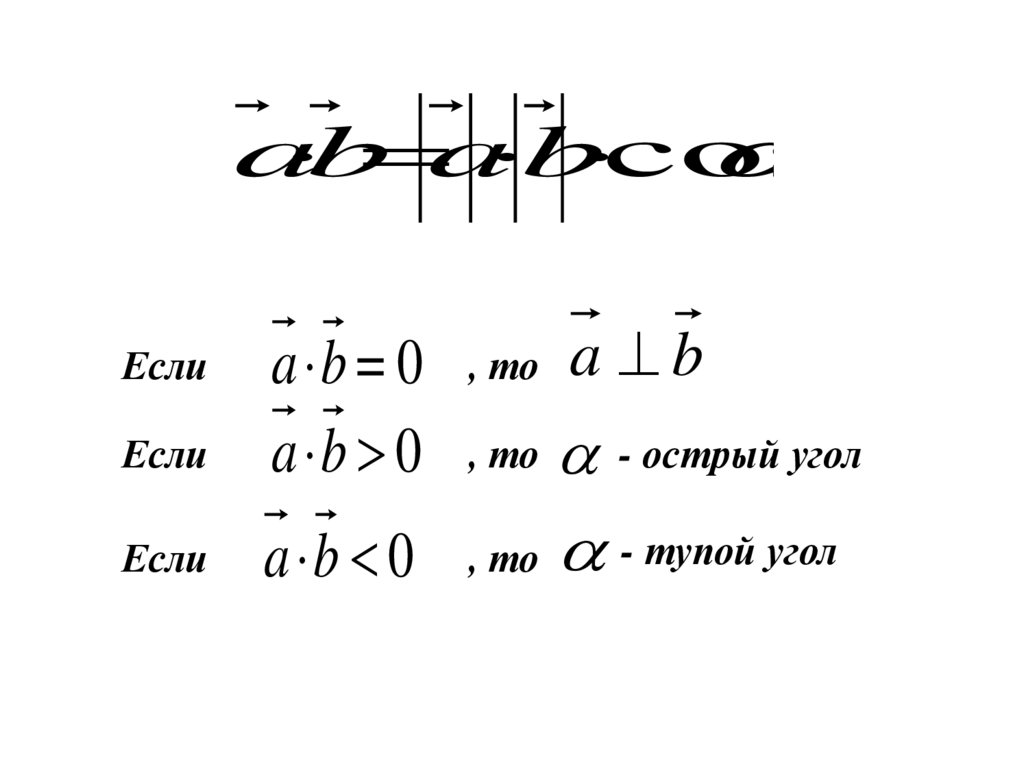








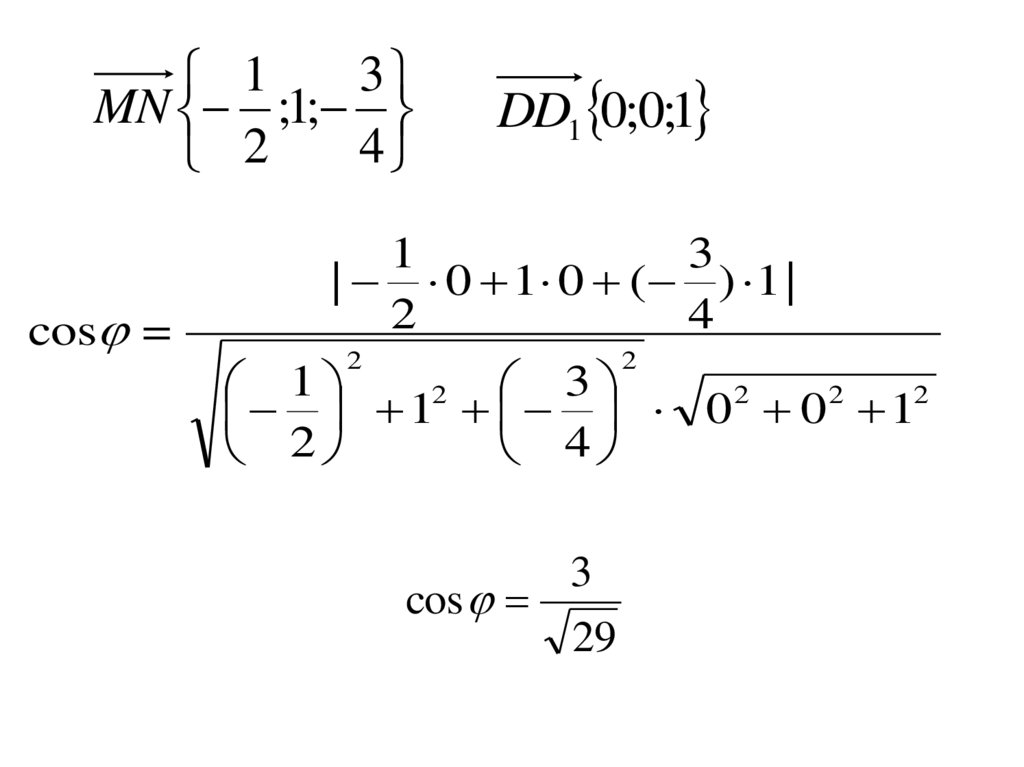

 Математика
Математика








